Punti di sintesi
- I metodi di meta-analisi combinano l’evidenza quantitativa di studi correlati per produrre risultati basati su un intero corpo di ricerca
- Gli studi che non forniscono prove dirette su un particolare risultato o confronto di interesse di un particolare trattamento sono spesso scartati da una meta-analisi di tale risultato o confronto di trattamento
- I metodi di meta-analisi multivariata e di meta-analisi in rete analizzano simultaneamente più esiti e più trattamenti, rispettivamente, il che permette a più studi di contribuire a ciascun esito e al confronto dei trattamenti
- I risultati riassuntivi per ogni risultato dipendono ora dai risultati correlati di altri risultati, e i risultati riassuntivi per ogni confronto di trattamento incorporano ora prove indirette da confronti di trattamento correlati, oltre a qualsiasi prova diretta.
- Questo porta spesso ad un guadagno di informazioni, che può essere quantificato dalla statistica del “prestito di forza”, BoS (la riduzione percentuale della varianza di un risultato di sintesi dovuta a prove correlate o indirette)
- In un’ipotesi mancante a caso, una meta-analisi multivariata di più esiti è più vantaggiosa quando gli esiti sono altamente correlati e la percentuale di studi con esiti mancanti è elevata.
- Le meta-analisi di rete acquisiscono informazioni attraverso un’ipotesi di coerenza, che dovrebbe essere valutata in ogni rete, ove possibile. Di solito c’è una bassa potenza per rilevare l’incoerenza, che si verifica quando i modificatori di effetto sono sistematicamente diversi nei sottoinsiemi di prove che forniscono prove dirette e indirette
- La meta-analisi di rete permette di confrontare più trattamenti e di classificarli in base ai loro risultati sommari. Concentrarsi sulla probabilità di essere classificati al primo posto è, tuttavia, potenzialmente fuorviante: un trattamento classificato al primo posto può anche avere un’alta probabilità di essere classificato all’ultimo posto, e il suo beneficio rispetto ad altri trattamenti può essere di scarso valore clinico
- Stanno emergendo nuovi metodi di meta-analisi in rete per utilizzare i dati dei singoli partecipanti, per valutare la dose, per incorporare le prove del “mondo reale” provenienti da studi osservazionali e per allentare l’ipotesi di coerenza, consentendo inferenze sommarie e tenendo conto degli effetti di incoerenza.
I metodi di meta-analisi combinano l’evidenza quantitativa di studi correlati per produrre risultati basati su un intero corpo di ricerca. In quanto tali, le meta-analisi sono parte integrante della medicina basata sull’evidenza e del processo decisionale clinico, per esempio per guidare quale trattamento dovrebbe essere raccomandato per una particolare condizione. La maggior parte delle meta-analisi si basa sulla combinazione dei risultati (ad esempio, le stime degli effetti del trattamento) estratti da pubblicazioni di studio o ottenuti direttamente dagli autori dello studio. Sfortunatamente, gli studi pertinenti possono non valutare le stesse serie di trattamenti ed esiti, che creano problemi per le meta-analisi. Ad esempio, in una meta-analisi di 28 studi per confrontare otto trattamenti trombolitici dopo un infarto miocardico acuto, non è realistico aspettarsi che ogni studio metta a confronto tutti e otto i trattamenti1; infatti in ogni studio è stato esaminato un diverso insieme di trattamenti, con il numero massimo di studi per trattamento solo otto. 1 Allo stesso modo, i risultati clinici rilevanti potrebbero non essere sempre disponibili. Ad esempio, in una meta-analisi per riassumere l’effetto prognostico dello stato del recettore del progesterone nel cancro dell’endometrio, quattro studi hanno fornito risultati sia per la sopravvivenza specifica al cancro che per la sopravvivenza libera da progressione, ma altri studi hanno fornito risultati solo per la sopravvivenza specifica al cancro (due studi) o per la sopravvivenza libera da progressione (11 studi). 2
Gli studi che non forniscono prove dirette su un particolare risultato o trattamento di interesse sono spesso esclusi da una meta-analisi che valuta tale risultato o trattamento. Ciò non è gradito, specialmente se i partecipanti sono altrimenti rappresentativi della popolazione, del contesto clinico e della condizione di interesse. Gli studi di ricerca richiedono costi e tempo considerevoli e comportano un coinvolgimento prezioso dei pazienti, e il semplice fatto di scartare i pazienti potrebbe essere visto come uno spreco di ricerca. 345 I modelli statistici per la meta-analisi multivariata e la meta-analisi di rete affrontano questo problema analizzando simultaneamente più risultati e più trattamenti, rispettivamente. Ciò consente a un maggior numero di studi di contribuire al confronto di ogni risultato e trattamento. Inoltre, oltre all’utilizzo di prove dirette, il risultato sommario per ogni risultato dipende ora dai risultati correlati di risultati correlati, e il risultato sommario per ogni confronto di trattamento incorpora ora prove indirette da confronti di trattamenti correlati. 67 La logica è che osservando le evidenze correlate si impara qualcosa sulle prove dirette mancanti di interesse e si ottengono così alcune informazioni che altrimenti si perdono; un concetto a volte statisticamente noto come “forza debitrice”. 68
Le meta-analisi multivariate e, in particolare, le meta-analisi di rete sono sempre più diffuse nelle riviste cliniche. Ad esempio, una revisione fino ad aprile 2015 ha identificato 456 meta-analisi di rete di studi randomizzati che valutano almeno quattro diversi interventi. 9 Solo sei di queste 456 sono state pubblicate prima del 2005, e 103 sono state pubblicate solo nel 2014, sottolineando un drammatico aumento della diffusione negli ultimi 10 anni (fig. 1). Il BMJ ha pubblicato più di qualsiasi altra rivista (28; 6,1%). Anche gli articoli metodologici e di tutorial sulla meta-analisi della rete sono aumentati di numero, passando da meno di cinque nel 2005 a più di 30 ogni anno dal 2012 (fig. 1). 10
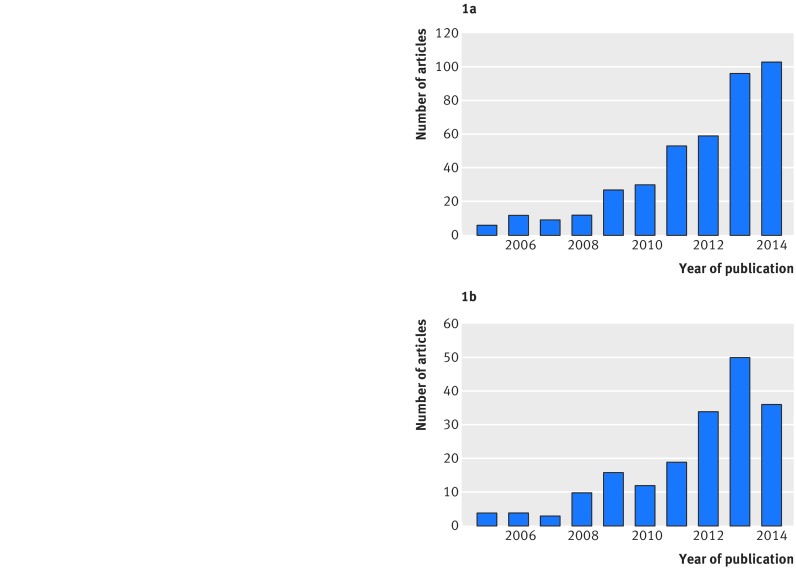
Fig. 1 Pubblicazione di articoli di meta-analisi in rete nel tempo. (a): Articoli applicati che riportano una revisione sistematica che utilizza la meta-analisi della rete per confrontare almeno quattro trattamenti pubblicati tra il 2005 e il 2014, come valutato da Petropoulou et al 2017.9 *Six sono stati pubblicati anche prima del 2005, e 43 sono stati pubblicati nel 2015 fino ad aprile. (b): Articoli metodologici, tutorial e articoli con valutazione empirica dei metodi per la meta-analisi della rete pubblicati tra il 2005 e il 2014, valutati da Efthimiou et al 201610 e disponibili su www.zotero.org/groups/wp4_-_network_meta-analysis.
Qui spieghiamo i concetti chiave, i metodi e i presupposti della meta-analisi multivariata e della rete, basandoci sui precedenti articoli di The BMJ. 111213 Iniziamo descrivendo l’uso di effetti correlati all’interno di una meta-analisi multivariata di risultati multipli e poi consideriamo l’uso di prove indirette all’interno di una meta-analisi di rete di trattamenti multipli. Evidenziamo anche due statistiche (BoS ed E) che riassumono le informazioni aggiuntive ottenute, e consideriamo le ipotesi chiave, le sfide e le nuove estensioni. Esempi reali sono incorporati in tutto il sistema.
Effetti correlati e meta-analisi multivariata di risultati multipli
Molti studi clinici hanno più di una variabile di esito; questa è la norma piuttosto che l’eccezione. Queste variabili sono raramente indipendenti e quindi ognuna di esse deve contenere alcune informazioni sulle altre. Se possiamo usare queste informazioni, dobbiamo farlo.
Bland 201114
Molti esiti clinici sono correlati tra loro, come la pressione sanguigna sistolica e diastolica nei pazienti con ipertensione, il livello di dolore e nausea nei pazienti con emicrania, e i tempi di sopravvivenza libera da malattia e globale nei pazienti con cancro. Tale correlazione a livello individuale porterà ad una correlazione tra gli effetti a livello di popolazione (studio). Ad esempio, in uno studio randomizzato di trattamento antipertensivo, è probabile che gli effetti del trattamento stimato per la pressione arteriosa sistolica e diastolica siano altamente correlati. Analogamente, in uno studio di coorte sul cancro, è probabile che gli effetti prognostici stimati di un biomarcatore siano altamente correlati per la sopravvivenza libera da malattia e la sopravvivenza complessiva. Gli effetti correlati si manifestano anche in molte altre situazioni, come quando ci sono più punti temporali (dati longitudinali),15 biomarcatori multipli e fattori genetici che sono interrelati,16 dimensioni di effetti multipli corrispondenti a insiemi sovrapposti di fattori di aggiustamento,17 misure multiple di accuratezza o performance (ad esempio, in relazione a un test diagnostico o a un modello di previsione),18 e misure multiple dello stesso costrutto (ad esempio, punteggi da diverse scale di punteggio del dolore, o valori del biomarcatore da diverse tecniche di misurazione di laboratorio19). In questo articolo ci si riferisce a questi come risultati multipli correlati.
Come nota Bland,14 la correlazione tra i risultati è potenzialmente informativa e vale la pena utilizzarla. Una meta-analisi multivariata affronta questo aspetto analizzando tutti i risultati correlati congiuntamente. Ciò si ottiene di solito assumendo distribuzioni normali multivariate,720 e generalizza i metodi di meta-analisi standard (univariata) descritti in precedenza nel BMJ. 12 Si noti che i risultati non sono amalgamati in un unico risultato; l’approccio multivariato produce comunque un risultato riassuntivo distinto per ogni risultato. Tuttavia, la correlazione tra i risultati è ora incorporata e questo porta due grandi vantaggi rispetto a una meta-analisi univariata di ciascun risultato separatamente. In primo luogo, l’incorporazione della correlazione consente di utilizzare i dati di sintesi di ogni risultato per tutti gli esiti. In secondo luogo, gli studi che non riportano tutti i risultati di interesse possono ora essere inclusi. 21 Ciò consente di includere più studi e prove e di conseguenza può portare a conclusioni più precise (intervalli di confidenza più ristretti). Ulteriori dettagli tecnici e opzioni software sono forniti nel materiale supplementare 1.22232425 Illustriamo i concetti chiave attraverso due esempi.
Esempio 1: Effetto prognostico del progesterone per la sopravvivenza specifica del cancro nell’endometrio
Nell’esempio del cancro endometriale, mancano i risultati prognostici per la sopravvivenza specifica del cancro in 11 studi (1412 pazienti) che forniscono risultati per la sopravvivenza libera da progressione. Una meta-analisi tradizionale univariata per la sopravvivenza specifica del cancro semplicemente scarta questi 11 studi, ma vengono mantenuti in un’analisi multivariata della sopravvivenza libera da progressione e della sopravvivenza specifica del cancro, che utilizza la loro forte correlazione positiva (circa 0,8). Questo porta a importanti differenze nei risultati di sintesi, come mostrato per la sopravvivenza specifica del cancro nella trama forestale della figura 2. La meta-analisi univariata per la sopravvivenza specifica al cancro include solo i sei studi con evidenza diretta e fornisce un rapporto di rischio sommario di 0,61 (intervallo di confidenza del 95% da 0,38 a 1,00; I2=70%), con l’intervallo di confidenza che supera il valore di nessun effetto. La meta-analisi multivariata include 17 studi e fornisce un rapporto di rischio sommario per la sopravvivenza specifica del cancro di 0,48 (0,29 a 0,79), con un intervallo di confidenza più stretto e una maggiore evidenza che il progesterone è prognostico per la sopravvivenza specifica del cancro. Quest’ultimo risultato è anche più simile all’effetto prognostico per la sopravvivenza libera da progressione (rapporto di rischio sommario 0,43, intervallo di confidenza del 95% da 0,26 a 0,71, da meta-analisi multivariata), come forse ci si potrebbe aspettare.
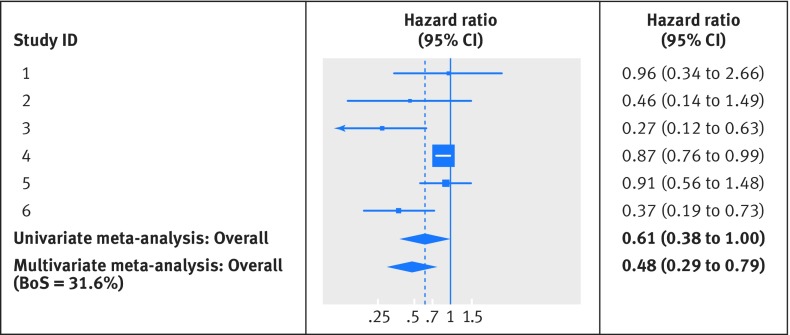
Fig 2 Trama forestale per l’effetto prognostico del progesterone sulla sopravvivenza specifica del cancro nell’endometrio, con risultati sommari per la meta-analisi univariata e multivariata. La meta-analisi multivariata della sopravvivenza specifica del cancro e della sopravvivenza libera da progressione ha utilizzato l’approccio di Riley et al per gestire le correlazioni mancanti all’interno dello studio, attraverso una stima limitata della massima probabilità. 26 L’eterogeneità è stata simile sia nelle meta-analisi univariate che multivariate (I2=70%)

Fig. 2 Trama forestale per l’effetto prognostico del progesterone sulla sopravvivenza specifica del cancro nell’endometrio, con risultati sommari per la meta-analisi univariata e multivariata. La meta-analisi multivariata della sopravvivenza specifica del cancro e della sopravvivenza libera da progressione ha utilizzato l’approccio di Riley et al per gestire le correlazioni mancanti all’interno dello studio, attraverso una stima limitata della massima probabilità. 26 L’eterogeneità è stata simile sia nelle meta-analisi univariate che multivariate (I2=70%)
Esempio 2: La concentrazione di fibrinogeno plasmatico come fattore di rischio per le malattie cardiovascolari
La Fibrinogen Studies Collaboration esamina se la concentrazione di fibrinogeno nel plasma è un fattore di rischio indipendente per le malattie cardiovascolari utilizzando i dati di 31 studi. 17 Tutti i 31 studi hanno permesso di ottenere un rapporto di rischio parzialmente regolato, dove il rapporto di rischio per il fibrinogeno è stato regolato per lo stesso nucleo di fattori di rischio noti, tra cui l’età, il fumo, l’indice di massa corporea e la pressione sanguigna. Tuttavia, un rapporto di rischio più “completamente” aggiustato, ulteriormente aggiustato per il livello di colesterolo, il consumo di alcol, i livelli di trigliceridi e il diabete, è stato calcolabile solo in 14 studi. Quando le stime parzialmente e completamente corrette vengono tracciate in questi 14 studi, c’è una forte correlazione positiva (quasi 1, cioè un’associazione quasi perfetta lineare) tra di loro (fig. 3).
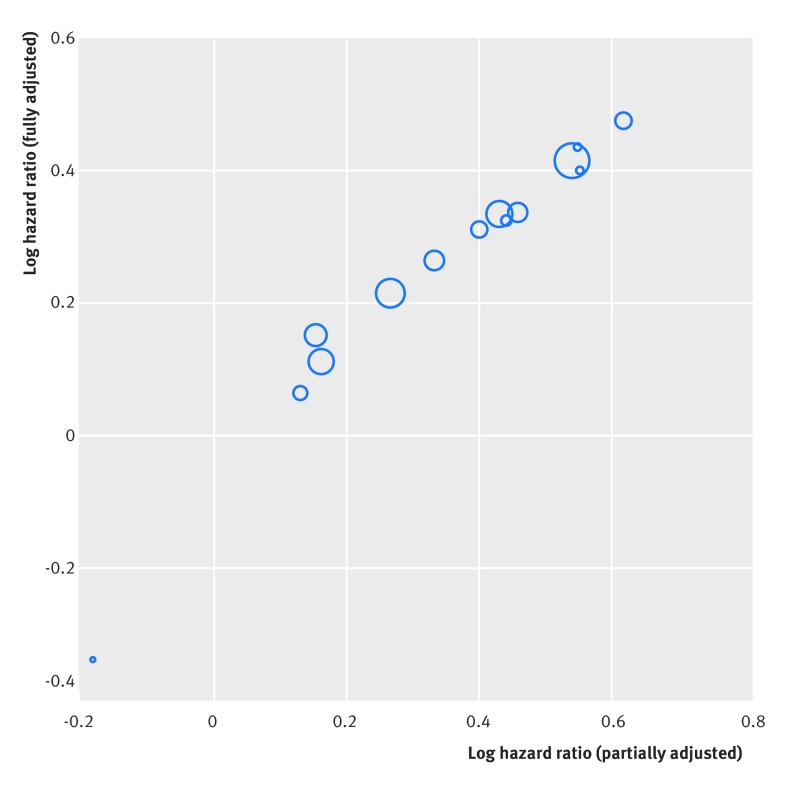
Fig. 3 Forte correlazione osservata (associazione lineare) tra le stime del rapporto di rischio logico dell’effetto regolato parzialmente e “completamente” del fibrinogeno sul tasso di malattie cardiovascolari. La dimensione di ogni cerchio è proporzionale alla precisione (inverso della varianza) della stima del rapporto di pericolo del log completamente aggiustato (cioè, cerchi più grandi indicano stime di studio più precise). I rapporti di pericolo sono stati ricavati in ogni studio separatamente da una regressione di Cox, indicando l’effetto di un aumento di 1 g/L dei livelli di fibrinogeno sul tasso di malattie cardiovascolari
Una meta-analisi standard (univariata) degli effetti casuali (univariata) delle prove dirette di 14 studi fornisce un rapporto di rischio completamente regolato di 1,31 (intervallo di confidenza del 95% da 1,22 a 1,42; I2=29%), che indica che un aumento di 1 g/L dei livelli di fibrinogeno è associato, in media, ad un aumento relativo del 31% del rischio di malattie cardiovascolari. Tuttavia, una meta-analisi multivariata di risultati parzialmente e completamente aggiustati incorpora le informazioni di tutti i 31 studi, e quindi di altri 17 studi (>70.000 pazienti), per utilizzare la grande correlazione (vicino a 1). Ciò produce lo stesso rapporto di rischio sommario completamente corretto di 1,31, ma fornisce un intervallo di confidenza più preciso (da 1,25 a 1,38) grazie alle informazioni supplementari ottenute (vedi la parcella forestale nel materiale supplementare 2).

Fig. 3 Forte correlazione osservata (associazione lineare) tra le stime del log hazard ratio dell’effetto regolato parzialmente e “completamente” del fibrinogeno sul tasso di malattie cardiovascolari. La dimensione di ogni cerchio è proporzionale alla precisione (inverso della varianza) della stima del rapporto di pericolo del log completamente aggiustato (cioè, cerchi più grandi indicano stime di studio più precise). I rapporti di pericolo sono stati ricavati in ogni studio separatamente da una regressione di Cox, indicando l’effetto di un aumento di 1 g/L dei livelli di fibrinogeno sul tasso di malattie cardiovascolari
Evidenze indirette e meta-analisi in rete di più trattamenti
Consideriamo ora la valutazione di più trattamenti. Una meta-analisi che valuta un particolare trattamento a confronto (ad esempio, trattamento A v trattamento B) utilizzando solo l’evidenza diretta è nota come meta-analisi a coppie. Quando l’insieme dei trattamenti differisce da uno studio all’altro, questo approccio può ridurre notevolmente il numero di studi per ogni meta-analisi e rende difficile il confronto formale di più di due trattamenti. Una meta-analisi di rete affronta questo problema sintetizzando tutti gli studi nella stessa analisi e utilizzando l’evidenza indiretta. 222728Considerate una semplice meta-analisi di rete di tre trattamenti (A, B e C) valutati in precedenti studi randomizzati. Si supponga che l’effetto relativo del trattamento (cioè il contrasto del trattamento) di A contro B sia di interesse fondamentale e che alcuni studi confrontino direttamente il trattamento A con B. Tuttavia, esistono anche altri studi del trattamento A contro C e altri studi del trattamento B contro C, che non forniscono alcuna prova diretta del beneficio del trattamento A contro B, in quanto non hanno esaminato entrambi i trattamenti. Le prove indirette del trattamento A contro B possono ancora essere ottenute da questi studi sotto il cosiddetto presupposto della “coerenza” che, in media, in tutti gli studi, indipendentemente dai trattamenti confrontati:
dove il contrasto del trattamento è, ad esempio, un rischio relativo log, il rapporto di probabilità log, il rapporto di pericolo log o la differenza media. Questa relazione si manterrà sempre esattamente all’interno di qualsiasi studio randomizzato in cui vengono esaminati i trattamenti A, B e C. È, tuttavia, plausibile che si mantenga (in media) anche all’interno di quegli studi che confrontano solo un insieme ridotto di trattamenti, se le caratteristiche cliniche e metodologiche (come la qualità, la durata del follow-up, il case mix) sono simili in ogni sottoinsieme (in questo caso, gli studi di trattamento A v B, A v C e B v C). In questa situazione, il beneficio del trattamento A contro B può essere dedotto dall’evidenza indiretta confrontando gli studi del solo trattamento A contro C con gli studi del solo trattamento B contro C, oltre all’evidenza diretta proveniente dagli studi del trattamento A contro B (fig 4).
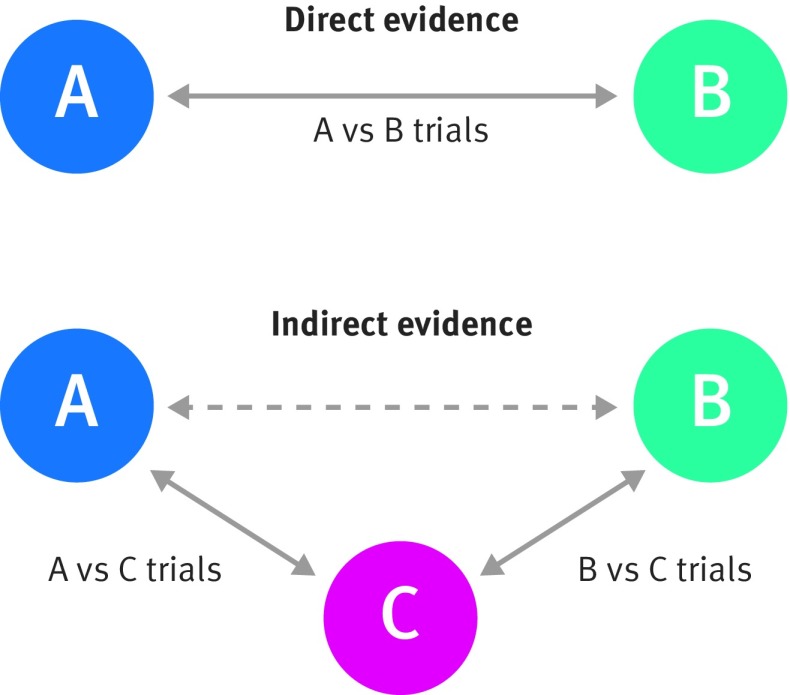
Fig. 4 Rappresentazione visiva delle evidenze dirette e indirette per il confronto tra A e B (adattato da Song et al 201129)
Sotto questa ipotesi di coerenza ci sono diverse opzioni per specificare un modello di meta-analisi di rete, a seconda del tipo di dati disponibili. Se ci sono solo due trattamenti (cioè un confronto di trattamento) per ogni prova, allora l’approccio più semplice è una meta-regressione standard, che modella le stime dell’effetto del trattamento tra le prove in relazione a un trattamento di riferimento. La scelta del trattamento di riferimento è arbitraria e non fa alcuna differenza per i risultati della meta-analisi. Questa può essere estesa ad una meta-regressione multivariata per accogliere studi con tre o più gruppi (spesso chiamati studi multi-braccio). 3031 Piuttosto che modellare direttamente le stime dell’effetto del trattamento, per un risultato binario è più comune usare un quadro logistico di regressione per modellare direttamente i numeri e gli eventi disponibili per ogni gruppo di trattamento (braccio). Allo stesso modo, una regressione lineare o regressione di Poisson potrebbe essere usata per modellare direttamente gli esiti e i tassi continui in ogni gruppo in ogni studio. Nel fare ciò è importante mantenere la randomizzazione e il raggruppamento dei pazienti all’interno degli studi30 e incorporare effetti casuali per consentire l’eterogeneità tra gli studi nell’ampiezza degli effetti del trattamento. 12 Il materiale supplementare 1 fornisce maggiori dettagli tecnici (e opzioni software2832) per la meta-analisi in rete e una spiegazione statistica più completa viene fornita altrove. 30
Dopo la stima di una meta-analisi di rete, si ottiene un risultato riassuntivo per ogni trattamento relativo al trattamento di riferimento scelto. Successivamente, altri confronti (contrasti di trattamento) vengono poi ricavati utilizzando la relazione di coerenza. Ad esempio, se C è il trattamento di riferimento in una meta-analisi di rete di un risultato binario, allora il rapporto di log log log di sintesi (logOR) per il trattamento A contro B si ottiene dalla differenza tra la stima di logOR di sintesi per il trattamento A contro C e la stima di logOR di sintesi per il trattamento B contro C. Illustriamo ora i concetti chiave attraverso un esempio.

Fig. 4 Rappresentazione visiva delle prove dirette e indirette per il confronto tra A e B (adattato da Song et al 201129)
Esempio 3: Confronto di otto trattamenti trombolitici dopo un infarto miocardico acuto
Nella meta-analisi dei trombolitici,1 l’obiettivo era quello di stimare l’efficacia relativa di otto trattamenti concorrenti nel ridurre le probabilità di mortalità di 30-35 giorni; questi trattamenti sono etichettati come da A ad H per brevità (vedi figura 5 per i nomi completi). Una versione di questo set di dati contenente sette trattamenti è stata precedentemente pubblicata su The BMJ da Caldwell et al,13 e le nostre indagini estendono questo lavoro.
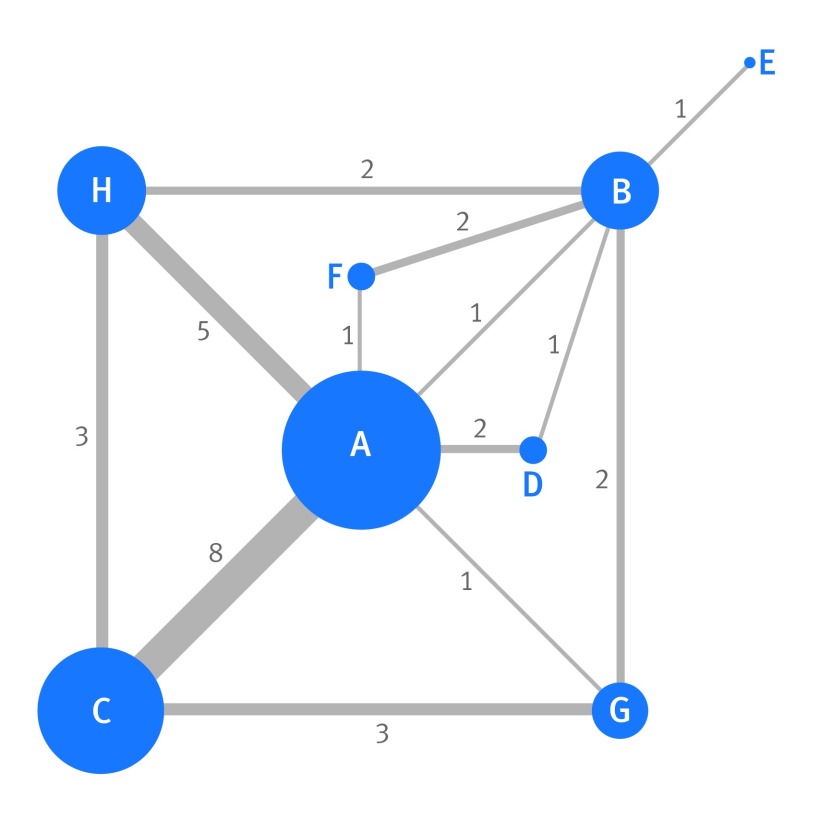
Fig. 5 Mappa in rete dei confronti diretti disponibili nei 28 studi che esaminano l’effetto di otto trombolitici (etichettati da A ad H) sulla mortalità a 30-35 giorni in pazienti con infarto miocardico acuto. Ogni nodo (cerchio) rappresenta un trattamento diverso, e la sua dimensione è proporzionale al numero di studi in cui viene direttamente esaminato. La larghezza della linea che unisce due nodi è proporzionale al numero di prove che confrontano direttamente i due rispettivi trattamenti (il numero è anche mostrato accanto alla linea). Se nessuna linea unisce direttamente due nodi (ad esempio, i trattamenti C e D), ciò indica che nessuna prova ha confrontato direttamente i due rispettivi trattamenti. A=streptochinasi; B=alteplasi accelerata; C=alteplasi; D=streptochinasi+alteplasi; E=tenecteplasi; F=reteplasi; G=urochinasi; H=antistreptilasi
Con otto trattamenti ci sono 28 confronti a coppie di potenziale interesse; tuttavia, solo 13 di questi sono stati direttamente riportati in almeno uno studio. Ciò è dimostrato dalla rete di prove (fig. 5), dove ogni nodo è un particolare trattamento e una linea collega due nodi quando almeno una prova confronta direttamente i due rispettivi trattamenti. Ad esempio, un confronto diretto del trattamento C contro A è disponibile in otto studi, mentre un confronto diretto del trattamento F contro A è disponibile solo in uno studio. Con tale discrepanza nella quantità di prove dirette disponibili per ogni trattamento e tra ogni coppia di trattamenti è estremamente problematico confrontare gli otto trattamenti utilizzando solo metodi di meta-analisi standard (univariata) a coppie.
Pertanto, utilizzando il numero di pazienti e di decessi per 30-35 giorni in ogni gruppo di trattamento, abbiamo applicato una meta-analisi di rete attraverso un modello di meta-regressione a effetti casuali multivariati per ottenere i rapporti di probabilità sommarie per i trattamenti da B ad H contro A e successivamente tutti gli altri contrasti. 2831 Ciò ha permesso di incorporare tutti i 28 studi e di confrontare tutti gli otto trattamenti simultaneamente, utilizzando l’evidenza diretta e anche l’evidenza indiretta propagata attraverso la rete attraverso l’ipotesi di coerenza. La scelta del gruppo di riferimento non modifica i risultati, che sono mostrati in figura 6 e materiale supplementare 3. L’evidenza indiretta ha un impatto importante su alcuni confronti di trattamento. Per esempio, l’effetto di trattamento sommario di H contro B nella meta-analisi di rete di tutti i 28 studi (odds ratio 1.19, intervallo di confidenza del 95% da 1.06 a 1.35) è sostanzialmente diverso da una meta-analisi standard a coppie di due studi (odds ratio sommario 3.87, intervallo di confidenza del 95% da 1.74 a 8.58).
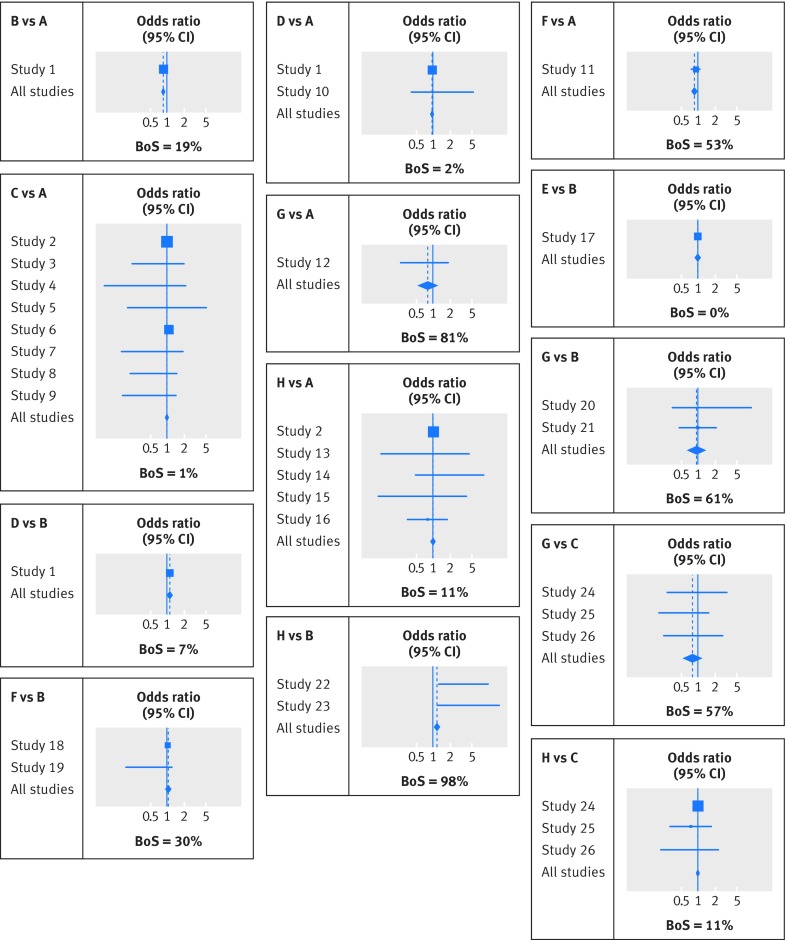
Fig 6 Trama forestale estesa che mostra i risultati della meta-analisi della rete per tutti i confronti in cui erano disponibili prove dirette in almeno una prova. Ogni quadrato denota la stima del rapporto di probabilità per quello studio, con la dimensione del quadrato proporzionale al numero di pazienti in quello studio, e la corrispondente linea orizzontale denota l’intervallo di confidenza. Il centro di ogni diamante denota il rapporto delle quote sommarie dalla meta-analisi della rete, e la larghezza del diamante fornisce il suo intervallo di confidenza del 95%. BoS denota l’indebitamento della statistica di forza, che può variare dallo 0% al 100%.

Fig 5 Mappa in rete dei confronti diretti disponibili nei 28 studi che esaminano l’effetto di otto trombolitici (etichettati da A ad H) sulla mortalità a 30-35 giorni in pazienti con infarto miocardico acuto. Ogni nodo (cerchio) rappresenta un trattamento diverso, e la sua dimensione è proporzionale al numero di studi in cui viene direttamente esaminato. La larghezza della linea che unisce due nodi è proporzionale al numero di prove che confrontano direttamente i due rispettivi trattamenti (il numero è anche mostrato accanto alla linea). Se nessuna linea unisce direttamente due nodi (ad esempio, i trattamenti C e D), ciò indica che nessuna prova ha confrontato direttamente i due rispettivi trattamenti. A=streptochinasi; B=alteplasi accelerata; C=alteplasi; D=streptochinasi+alteplasi; E=tenecteplasi; F=reteplasi; G=urochinasi; H=antistreptilasi

Fig 6 Trama forestale estesa che mostra i risultati della meta-analisi della rete per tutti i confronti in cui erano disponibili prove dirette in almeno una prova. Ogni quadrato denota la stima del rapporto di probabilità per quello studio, con la dimensione del quadrato proporzionale al numero di pazienti in quello studio, e la corrispondente linea orizzontale denota l’intervallo di confidenza. Il centro di ogni diamante denota il rapporto delle quote sommarie dalla meta-analisi della rete, e la larghezza del diamante fornisce il suo intervallo di confidenza del 95%. BoS denota l’indebitamento della statistica di forza, che può variare dallo 0% al 100%.
Classifica dei trattamenti
Dopo una meta-analisi di rete è utile classificare i trattamenti in base alla loro efficacia. Questo processo di solito, anche se non sempre,33 richiede l’uso di metodi di simulazione o di ricampionamento. 283134 Tali metodi utilizzano migliaia di campioni della distribuzione (approssimativa) degli effetti del trattamento sommario, per identificare la percentuale di campioni (probabilità) che ogni trattamento ha l’effetto più (o meno) benefico. Il pannello A nella figura 7 mostra la probabilità che ogni trattamento trombolitico sia stato classificato come il più efficace tra tutti i trattamenti, e in modo simile secondo, terzo, e così via fino al meno efficace. Il trattamento G ha la più alta probabilità (51,7%) di essere il più efficace nel ridurre le probabilità di mortalità di 30-35 giorni, seguito dai trattamenti E (21,5%) e B (18,3%).
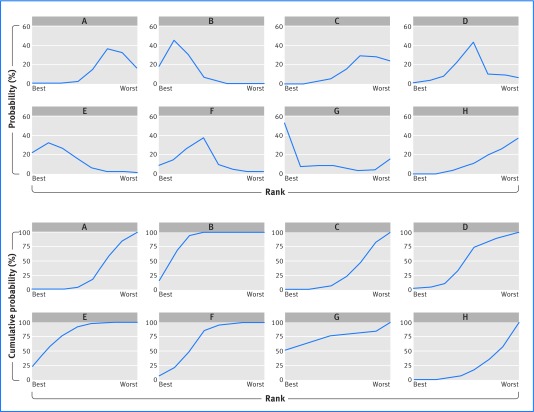
Fig. 7 Grafici della probabilità di classificazione per ogni trattamento considerato nella meta-analisi della rete trombolitica. (pannello superiore) la scala delle probabilità; (pannello inferiore) la scala delle probabilità cumulative
Concentrarsi sulla probabilità di essere classificati al primo posto è potenzialmente fuorviante: un trattamento classificato al primo posto potrebbe anche avere un’alta probabilità di essere classificato all’ultimo posto,35 e il suo beneficio rispetto ad altri trattamenti potrebbe essere di scarso valore clinico. Nel nostro esempio, il trattamento G ha la più alta probabilità di essere più efficace, ma l’effetto di sintesi per G è simile a quello dei trattamenti B ed E, ed è improbabile che la loro differenza sia clinicamente importante. Inoltre, il trattamento G ha anche la quarta maggiore probabilità di essere il meno efficace (14,4%), riflettendo un grande effetto di sintesi con un ampio intervallo di confidenza. Al contrario, i trattamenti B, E e F hanno una bassa probabilità (vicina allo 0%) di essere meno efficaci. Quindi, un trattamento può avere la più alta probabilità di essere classificato al primo posto, quando in realtà non c’è una forte evidenza (oltre il caso) che sia migliore di altri trattamenti disponibili. Per illustrare ulteriormente questo aspetto, aggiungiamo alla rete dei trombolitici un ipotetico nuovo farmaco, chiamato Brexitocin, per il quale non esistono prove dirette o indirette. Data la mancanza di prove, Brexitocin ha essenzialmente il 50% di probabilità di essere il trattamento più efficace, ma anche il 50% di essere il meno efficace.
Per aiutare a risolvere questo problema, sono utili il rango medio e la superficie sotto la curva di RAnking cumulativo (SUCRA). 3637 Il rango medio fornisce la posizione media per ogni trattamento. Il SUCRA è l’area sotto un grafico a linee della probabilità cumulativa sopra i ranghi (dal più efficace al meno efficace) (pannello B in fig 7) ed è solo il rango medio scalato per essere tra 0 e 1. Una misura simile è il punteggio P. 33 Per la rete trombolitica (ora esclusa la Brexitocina), i trattamenti B ed E hanno i migliori ranghi medi (rispettivamente 2.3 e 2.6), seguiti dal trattamento G (3.0). Quindi, anche se il trattamento G aveva la più alta probabilità di essere classificato al primo posto, in base al rango medio è ora al terzo posto.

Fig. 7 Grafici della probabilità di classificazione per ogni trattamento considerato nella meta-analisi della rete trombolitica. (pannello superiore) la scala delle probabilità; (pannello inferiore) la scala delle probabilità cumulative
Quantificare le informazioni ottenute da prove correlate o indirette
Copas et al (comunicazione personale, 2017) propongono che, rispetto ad una meta-analisi multivariata o di rete con la stessa ampiezza tra le eterogeneità dello studio, una meta-analisi standard (univariata) della sola evidenza diretta è simile a buttare via il 100×(1-E)% degli studi disponibili. L’efficienza (E) è definita come il:
dove l’evidenza correlata si riferisce a prove indirette o correlate (o entrambe) e la varianza si riferisce alla scala originale della meta-analisi (quindi tipicamente il rischio relativo log, il log odds ratio, il log hazard ratio o la differenza media). Per esempio, se E=0,9 allora una meta-analisi standard è simile a buttare via il 10% degli studi e dei pazienti (e degli eventi) disponibili.
Definiamo n anche come numero di studi disponibili con evidenza diretta (cioè quelli che contribuirebbero a una meta-analisi standard). Quindi, le informazioni supplementari ottenute verso un particolare risultato di meta-analisi sommaria utilizzando prove indirette o correlate possono essere espresse come se avessero trovato prove dirette da un numero specifico di studi supplementari di dimensioni simili agli n studi (vedi equazione 1 nella figura 8). Per esempio, se ci sono nove studi che forniscono prove dirette di un risultato per una meta-analisi univariata standard ed E=0.9, allora il vantaggio di usare una meta-analisi multivariata è simile a quello di trovare prove dirette per quel risultato da un ulteriore studio (vedi equazione 2 in figura 8 per la derivazione). Si guadagna così il considerevole tempo, sforzo e denaro investito in circa uno studio di ricerca.

Fig. 8 Equazioni utilizzate per produrre figure nel testo
Jackson et al. propongono anche la statistica del prestito di forza (BoS)8 , che può essere calcolata per ogni risultato riassuntivo all’interno di una meta-analisi multivariata o di rete (vedi equazione 3 nella figura 8).
Il BoS fornisce la percentuale di riduzione della varianza di un risultato sintetico che deriva da (è preso in prestito da) evidenze correlate o indirette. Un modo equivalente di interpretare la BoS è la percentuale di peso nella meta-analisi che viene data all’evidenza correlata o indiretta. 8 Per esempio, in una meta-analisi di rete, una BoS dello 0% indica che il risultato sommario è basato solo sull’evidenza diretta, mentre una BoS del 100% indica che si basa interamente sull’evidenza indiretta. Riley et al. mostrano come ricavare i pesi percentuali di studio per i modelli di meta-analisi multiparametrica, comprese le meta-analisi di rete e le meta-analisi multivariate. 38

Fig. 8 Equazioni utilizzate per produrre figure nel testo
Applicazione agli esempi
Nell’esempio del fibrinogeno, l’indice di rischio riassuntivo completamente corretto ha un grande BoS del 53%, indicando che l’evidenza correlata (dai risultati parzialmente corretti) contribuisce per il 53% del peso totale al risultato riassuntivo. L’efficienza (E) è di 0,47, e quindi l’utilizzo delle prove correlate equivale ad aver trovato risultati completamente aggiustati da circa 16 studi aggiuntivi (vedere l’equazione 4 nella figura 8 per la derivazione).
Nell’esempio del progesterone, il BoS è del 33% per la sopravvivenza specifica del cancro, indicando che l’utilizzo dei risultati per la sopravvivenza libera da progressione riduce del 33% la varianza del rapporto di rischio del registro riassuntivo per la sopravvivenza specifica del cancro. Questo corrisponde ad una E di 0,67, e le informazioni ottenute dalla meta-analisi multivariata possono essere considerate simili ad aver trovato risultati di sopravvivenza specifica per il cancro da altri tre studi (vedi equazione 5 nella figura 8 per la derivazione).
Per la meta-analisi dei trombolitici, la BoS è mostrata in figura 6 per ogni confronto di trattamento dove c’erano prove dirette per almeno uno studio. Il valore è spesso grande. Per esempio, il BoS per il trattamento H contro B è del 97,8%, poiché ci sono solo due studi con prove dirette. Questo è simile a trovare prove dirette per il trattamento H contro B da altri 89 studi (vedi l’equazione 6 nella figura 8 per la derivazione) di dimensioni simili a quelle dei due studi esistenti. BoS è dello 0% per il trattamento E contro B, in quanto non c’erano prove indirette per questo confronto (fig. 6). Per i confronti non mostrati in figura 6, come il trattamento C contro B, il BoS è del 100% perché non c’erano prove dirette. Il materiale supplementare 3 mostra il peso percentuale (contributo) di ogni studio.
Sfide e ipotesi di meta-analisi multivariata o di rete
I nostri tre esempi mostrano il valore potenziale della meta-analisi multivariata e della rete e altri vantaggi sono discussi altrove. 152039 Gli approcci hanno tuttavia dei limiti.
I benefici di una meta-analisi multivariata possono essere piccoli
I modelli multivariati e univariati forniscono generalmente stime puntuali simili, anche se i modelli multivariati tendono a fornire stime più precise. Non è chiaro, tuttavia, quanto spesso questa precisione aggiunta cambierà qualitativamente le conclusioni delle revisioni sistematiche
Trikalinos et al 201440
Questa argomentazione, basata su prove empiriche,40 potrebbe essere livellata sull’esempio del fibrinogeno. Anche se c’è stato un notevole guadagno di precisione nell’uso della meta-analisi multivariata (BoS=53%), il fibrinogeno è stato chiaramente identificato come un fattore di rischio per le malattie cardiovascolari sia nelle analisi univariate che multivariate, e quindi le conclusioni non sono cambiate. Una controsintesi è che questo di per sé è utile sapere.
L’importanza potenziale di una meta-analisi multivariata di risultati multipli è maggiore quando BoS ed E sono grandi, il che è più probabile quando:
- la proporzione di studi senza prove dirette di un risultato di interesse è grande
- i risultati per altri risultati sono disponibili negli studi in cui non viene riportato un risultato di interesse
- l’entità della correlazione tra i risultati è grande (ad esempio, >0,5 o < -0,5), sia all’interno degli studi o tra gli studi.
Secondo la nostra esperienza, BoS ed E sono di solito i più grandi in una rete di meta-analisi di trattamenti multipli – cioè, si ottengono più informazioni su trattamenti multipli attraverso l’assunzione di consistenza che non su risultati multipli attraverso la correlazione. Una meta-analisi multivariata di più esiti è meglio riservata ad un insieme di esiti altamente correlati, perché altrimenti BoS ed E sono di solito piccole. Tali risultati dovrebbero essere identificati e specificati prima dell’analisi, ad esempio utilizzando il giudizio clinico e le conoscenze statistiche, in modo da evitare il dragaggio dei dati su diversi gruppi di risultati. Una meta-analisi multivariata di più esiti è anche meglio riservata ad una situazione con esiti mancanti (a livello di studio), in quanto l’evidenza aneddotica suggerisce che la BoS per un esito è approssimativamente delimitata dalla percentuale di dati mancanti per quell’esito. Ad esempio, nell’esempio del fibrinogeno, la percentuale di studi con un risultato completamente corretto mancante è del 55% (=100%×17/31), e quindi l’approccio multivariato è segnalato come utile, poiché la BoS potrebbe essere fino al 55% per il risultato completamente corretto. Come discusso, l’effettivo BoS era del 53% e quindi vicino al 55%, a causa della quasi perfetta correlazione tra effetti parzialmente e completamente aggiustati. Al contrario, in situazioni con dati completi o con una bassa percentuale di risultati mancanti, è improbabile che la BoS (e quindi una meta-analisi multivariata) sia importante. Inoltre, la meta-analisi multivariata non può gestire studi che non riportano nessuno degli esiti di interesse. Pertanto, sebbene la meta-analisi multivariata possa ridurre l’impatto della segnalazione selettiva degli esiti negli studi pubblicati, non può ridurre l’impatto della mancata pubblicazione di interi studi (distorsione della pubblicazione).
Se un confronto formale degli esiti correlati è interessante (ad esempio, per stimare la differenza tra gli effetti del trattamento sulla pressione sanguigna sistolica e diastolica), allora questo dovrebbe sempre essere fatto in un quadro multivariato, indipendentemente dalla quantità di dati mancanti, al fine di tenere conto delle correlazioni tra gli esiti ed evitare così intervalli di confidenza e valori P errati. 41 Allo stesso modo, una meta-analisi in rete di più trattamenti è preferibile anche se tutti gli studi esaminano tutti i trattamenti, poiché è necessario un unico quadro di analisi per stimare e confrontare gli effetti di ogni trattamento.
Le specifiche e le stime del modello non sono banali
Anche quando si prevede che la BoS sarà grande, le sfide potrebbero rimanere. 20 I modelli di meta-analisi multivariata e di rete sono spesso complessi, e il raggiungimento di una convergenza (cioè di stime affidabili dei parametri) può richiedere una semplificazione (ad esempio, comune tra i termini di varianza dello studio per ogni contrasto di trattamento, ipotesi di normalità multivariata), che può essere aperta al dibattito. 204243 Per esempio, in una meta-analisi multivariata di risultati multipli, i problemi di convergenza e di stima aumentano con l’aumentare del numero di risultati (e quindi di parametri sconosciuti), e quindi le applicazioni oltre i due o tre risultati sono rare. In particolare, a meno che non siano disponibili i dati dei singoli partecipanti44 ci possono essere problemi nell’ottenere e stimare le correlazioni tra i risultati4546; le possibili soluzioni includono un framework bayesiano che utilizza distribuzioni precedenti per parametri sconosciuti per portare informazioni esterne. 47
48
49
I benefici derivano da ipotesi
Ma la forza del prestito costruisce la debolezza. Costruisce la debolezza nel mutuatario perché rafforza la dipendenza da fattori esterni per ottenere le cose.
Covey 200850
Questa citazione si riferisce alle qualità necessarie per un leader efficace, ma è pertinente anche in questo caso. I vantaggi di una meta-analisi multivariata e di una meta-analisi di rete dipendono dal fatto che i risultati mancanti dello studio non sono casuali. 51 Partiamo dal presupposto che le relazioni che osserviamo in alcuni studi sono trasferibili ad altri studi dove non sono osservati. Per esempio, in una meta-analisi multivariata di risultati multipli, si suppone che l’associazione lineare osservata (correlazione) degli effetti per coppie di risultati (sia all’interno degli studi che tra gli studi) sia trasferibile ad altri studi in cui è disponibile solo uno dei risultati. Questa correlazione viene utilizzata anche per giustificare i risultati surrogati52 , ma spesso viene criticata e discussa. 53 La mancanza non casuale può essere più appropriata quando mancano i risultati a causa di una segnalazione selettiva degli esiti54 o di una scelta selettiva delle analisi. 55 Un approccio multivariato può comunque ridurre i pregiudizi di segnalazione selettiva in questa situazione39 , anche se non completamente.
In una meta-analisi di rete di confronti di trattamenti multipli, l’ipotesi di missingness è anche nota come transitività5657; essa implica che gli effetti relativi di tre o più trattamenti osservati direttamente in alcuni studi sarebbero gli stessi in altri studi dove non sono osservati. Sulla base di questo, l’ipotesi di coerenza è quindi valida. Quando le prove dirette e indirette non sono d’accordo, questa è nota come incoerenza (incoerenza). Una recente revisione di Veroniki et al. ha rilevato che circa una meta-analisi di rete su otto mostra incoerenza nel suo complesso58 , simile ad una revisione precedente. 29
Come possiamo esaminare l’incoerenza tra prove dirette e indirette?
I modificatori dell’effetto del trattamento si riferiscono alle caratteristiche metodologiche o cliniche degli studi che influenzano l’entità degli effetti del trattamento, e queste possono includere la durata del follow-up, le definizioni degli esiti, la qualità dello studio (rischio di distorsione), gli standard di analisi e di segnalazione (compreso il rischio di segnalazione selettiva) e le caratteristiche a livello del paziente. 29596061 Quando tali modificatori di effetto sono sistematicamente diversi nei sottoinsiemi di studi che forniscono prove dirette e indirette, ciò causa una vera e propria incoerenza. Pertanto, prima di intraprendere una meta-analisi di rete è importante selezionare solo gli studi rilevanti per la popolazione di interesse clinico e quindi identificare eventuali differenze sistematiche in tali studi che forniscano confronti diversi. Ad esempio, nella rete dei trombolitici, gli studi sul trattamento A contro C e sul trattamento A contro H sono sistematicamente diversi dagli studi sul trattamento C contro H in termini di potenziali modificatori di effetto? 62 Se è così, è probabile che ci sia un’incoerenza e quindi è meglio evitare un approccio di meta-analisi della rete.
Può essere difficile valutare il potenziale di incoerenza prima di una meta-analisi. Pertanto, dopo qualsiasi meta-analisi di rete, il potenziale di incoerenza dovrebbe essere esaminato statisticamente, anche se sfortunatamente questo spesso non viene fatto. 63 L’ipotesi di coerenza può essere esaminata per ogni confronto di trattamento dove c’è evidenza diretta e indiretta (vista come un anello chiuso all’interno della trama della rete)586465: qui l’approccio di separare l’evidenza indiretta da quella diretta65 (a volte chiamata scissione del nodo o scissione laterale) comporta la stima dell’evidenza diretta e indiretta e il confronto tra le due. L’ipotesi di coerenza può anche essere esaminata attraverso l’intera rete usando modelli di interazione design-by-treatment,3166 che permettono un test di significatività complessiva per l’incoerenza. Se si trovano prove di incoerenza, si dovrebbero cercare spiegazioni – per esempio, se l’incoerenza deriva da studi particolari con un disegno diverso o da quelli a più alto rischio di distorsione. 56 I modelli di rete potrebbero poi essere estesi per includere adeguate covariate esplicative o ridotti per escludere determinati studi. 62 Se l’incongruenza rimane inspiegabile, i termini di incongruenza possono invece essere modellati come effetti casuali con media zero, consentendo così stime sommarie complessive che consentano di ottenere un’incongruenza inspiegabile. 676869 Sono stati proposti altri approcci per la modellizzazione delle incoerenze64 e prevediamo ulteriori sviluppi in questo settore nei prossimi anni. Spesso, tuttavia, la potenza è troppo bassa per rilevare una vera incoerenza. 70
Nell’esempio dei trombolitici, l’approccio di separazione dell’evidenza indiretta da quella diretta non ha trovato alcuna incoerenza significativa, tranne che per il trattamento H contro B, visibile nella figura 6 come discrepanza tra lo studio 22, studio 23, e tutti gli studi della sottovoce “H v B“. Tuttavia, quando abbiamo applicato il modello di interazione design-by-treatment non c’era alcuna evidenza di incoerenza complessiva. Se gli studi di trattamento H contro B differiscono nella progettazione dagli altri studi, allora potrebbe essere ragionevole escluderli dalla rete, ma altrimenti un modello di incoerenza generale (con termini di incoerenza inclusi come effetti casuali) può fornire i migliori confronti di trattamento.
Nuove estensioni e temi caldi
Incorporazione di più trattamenti e di più esiti
Gli esempi precedenti hanno preso in considerazione sia esiti multipli che trattamenti multipli. Tuttavia, sta crescendo l’interesse ad accogliere entrambi insieme per aiutare a identificare il miglior trattamento attraverso molteplici esiti clinicamente rilevanti. 71727273747576 Ciò è realizzabile, ma è difficile a causa della maggiore complessità dei modelli statistici richiesti. Ad esempio, Efthimiou et al72 hanno eseguito una meta-analisi in rete di 68 studi che mettevano a confronto 13 farmaci anti-maniaci attivi e placebo per la mania acuta. Due risultati primari di interesse sono stati l’efficacia (definita come la percentuale di pazienti con almeno il 50% di riduzione dei sintomi maniacali dalla linea di base alla terza settimana) e l’accettabilità (definita come la percentuale di pazienti con interruzione del trattamento prima delle tre settimane). Questi sono probabilmente correlati negativamente (poiché i pazienti spesso interrompono il trattamento per mancanza di efficacia), così gli autori hanno esteso un quadro di meta-analisi in rete per analizzare congiuntamente questi risultati e tener conto della loro correlazione (stimata a circa -0,5). Ciò è particolarmente importante in quanto 19 dei 68 studi hanno fornito dati solo su uno dei due risultati. Rispetto al considerare ogni risultato separatamente, questo approccio produce intervalli di confidenza più ristretti per gli effetti sintetici del trattamento e ha un impatto sulla classificazione relativa di alcuni dei trattamenti (vedi materiale supplementare 4). In particolare, la carbamazepina si classifica come il trattamento più efficace in termini di risposta quando si considerano gli esiti separatamente, ma scende al quarto posto quando si tiene conto della correlazione.
Contabilità della dose e della classe
La meta-analisi standard della rete non tiene conto delle somiglianze tra i trattamenti. Quando alcuni trattamenti rappresentano dosi diverse dello stesso farmaco, i modelli di meta-analisi in rete possono essere estesi per incorporare relazioni dose-risposta sensate. 77 Allo stesso modo, quando i trattamenti possono essere raggruppati in più classi, i modelli di meta-analisi in rete possono essere estesi per consentire ai trattamenti nella stessa classe di avere effetti più simili rispetto ai trattamenti in classi diverse. 78
Utilizzo dei dati dei singoli partecipanti
La meta-analisi di rete che utilizza dati aggregati (pubblicati) è conveniente, ma a volte i rapporti pubblicati sono inadeguati a questo scopo, ad esempio se le misure di esito sono definite in modo diverso o se l’interesse risiede negli effetti del trattamento all’interno di sottogruppi. In questi casi può essere utile raccogliere i dati dei singoli partecipanti. 79 Di conseguenza, stanno emergendo metodi per la meta-analisi in rete dei dati dei singoli partecipanti. 6080818283838485 Uno dei principali vantaggi è che questi consentono l’inclusione di covariate a livello di partecipante, il che è importante se si tratta di modificatori di effetti che altrimenti causerebbero incoerenze nella rete.
Inclusione di prove del mondo reale
L’interesse sta crescendo nell’utilizzo di prove reali provenienti da studi non randomizzati, al fine di corroborare i risultati di studi randomizzati e di aumentare le prove utilizzate per prendere decisioni. I metodi di meta-analisi in rete vengono così estesi a questo scopo,86 e una recente panoramica è data da Efthimiou et al,87 che sottolineano l’importanza di assicurare la compatibilità dei diversi pezzi di prova per ogni confronto di trattamento.
Meta-analisi cumulativa della rete
Créquit et al88 mostrano che la quantità di prove randomizzate coperte dalle revisioni sistematiche esistenti di trattamenti di seconda linea concorrenti per il cancro polmonare avanzato non a piccole cellule era sempre sostanzialmente incompleta, con il 40% o più dei trattamenti, dei confronti tra i trattamenti e degli studi mancanti. Per affrontare questo problema, essi raccomandano un nuovo paradigma “passando da una serie di meta-analisi standard focalizzate su trattamenti specifici (molti trattamenti non sono considerati) a una singola meta-analisi di rete che copra tutti i trattamenti; e da meta-analisi eseguite in un dato momento e spesso non aggiornate a una meta-analisi di rete cumulativa sistematicamente aggiornata non appena i risultati di un nuovo studio diventano disponibili.”Quest’ultima è definita come una meta-analisi cumulativa di rete in diretta, e i vari passi, vantaggi e sfide di questo approccio meritano un’ulteriore considerazione. 88 Un concetto simile è il Framework for Adaptive MEta-analysis (FAME), che richiede la conoscenza delle prove in corso e suggerisce di programmare gli aggiornamenti della meta-analisi in coincidenza con le nuove pubblicazioni. 89
Valutazione della qualità e reporting
Infine, incoraggiamo la valutazione della qualità della meta-analisi della rete secondo le linee guida di Salanti et al90 e la comunicazione chiara dei risultati utilizzando le linee guida PRISMA-NMA. 91 Quest’ultima può essere arricchita dalla presentazione dei pesi percentuali dello studio secondo le recenti proposte,838 per rivelare il contributo di ogni studio agli effetti sintetici del trattamento.
Conclusioni
I metodi statistici per la meta-analisi multivariata e di rete utilizzano l’evidenza correlata e indiretta accanto all’evidenza diretta, e qui ne abbiamo evidenziato i vantaggi e le sfide. La Tabella 1 riassume la logica, i benefici e le potenziali insidie dei due approcci. Si spera che i set di risultati principali e la condivisione dei dati riducano il problema della mancanza di prove dirette,617992 ma è improbabile che lo risolvano completamente. Pertanto, per combinare l’evidenza indiretta e diretta in un quadro coerente, ci aspettiamo che le applicazioni e la metodologia per la meta-analisi multivariata e di rete continuino a crescere nei prossimi anni. 9
93
| Domanda | Meta-analisi multivariata di risultati multipli | Meta-analisi in rete dei confronti di trattamenti multipli |
|---|---|---|
| Qual è il contesto? | Gli studi di ricerca primaria riportano risultati diversi, e quindi una meta-analisi separata per ogni risultato utilizzerà studi diversi | Gli studi randomizzati valutano diverse serie di trattamenti, e quindi una meta-analisi separata (a coppie) per ogni confronto di trattamento (contrasto) utilizzerà studi diversi |
| Qual è la logica del metodo? | – Permettere che tutti i risultati e gli studi siano sintetizzati congiuntamente in un unico modello di meta-analisi – Rendere conto della correlazione tra i risultati per ottenere maggiori informazioni | – Permettere che tutti i trattamenti e gli studi siano sintetizzati congiuntamente in un unico modello di meta-analisi – Permettere l’incorporazione di prove indirette (ad esempio, sul trattamento A v B dalle prove del trattamento A v C e B v C) |
| Quali sono i vantaggi del metodo? | – La contabilizzazione della correlazione consente al risultato della meta-analisi di ogni risultato di utilizzare i dati per tutti gli esiti – Questo di solito porta a conclusioni più precise (intervalli di confidenza più ristretti) – Può ridurre l’impatto della segnalazione selettiva degli esiti | – Fornisce un quadro coerente di meta-analisi per riassumere e comparare (classificare) gli effetti di tutti i trattamenti contemporaneamente – L’incorporazione di prove indirette spesso porta a risultati riassuntivi sostanzialmente più precisi (intervalli di confidenza più ristretti) per ogni confronto di trattamento |
| Quando si dovrebbe considerare il metodo? | – Quando sono di interesse molteplici risultati correlati, con un’ampia correlazione tra loro (ad esempio, > 0,5 o < -0,5) e un’alta percentuale di studi con esiti mancanti; oppure – Quando è necessario un confronto formale degli effetti su diversi esiti | – Quando è necessario un confronto formale degli effetti di più trattamenti – Quando sono necessarie raccomandazioni sui migliori (o pochi migliori) trattamenti |
| Quali sono le potenziali insidie del metodo? | – Ottenere e stimare le correlazioni all’interno dello studio e tra gli studi è spesso difficile – Le informazioni ottenute utilizzando la correlazione sono spesso piccole e possono non modificare le conclusioni cliniche- Il metodo presuppone che gli esiti siano mancanti a caso, il che potrebbe non essere valido in presenza di una segnalazione selettiva degli esiti – Potrebbe essere necessario semplificare le ipotesi per trattare un gran numero di parametri di varianza sconosciuti | – L’evidenza indiretta nasce da un’ipotesi di coerenza: gli effetti relativi dei trattamenti ≥3 osservati direttamente in alcuni studi sono (in media) gli stessi in altri studi dove non sono osservati. Questa supposizione dovrebbe essere verificata, ma di solito c’è una bassa potenza per rilevare l’incoerenza – La classificazione dei trattamenti può essere fuorviante a causa di risultati sommari imprecisi – un trattamento classificato al primo posto può anche avere un’alta probabilità di essere classificato all’ultimo posto – Può essere necessario semplificare le supposizioni per affrontare un gran numero di parametri di varianza sconosciuti |
References
- J Am Stat Assoc. 2006; 101:447-59. DOI
- World J Surg Oncol. 2015; 13:208. Publisher Full Text | DOI | PubMed
- Lancet. 2014; 383:101-4. Publisher Full Text | DOI | PubMed
- Lancet. 2014; 383:267-76. Publisher Full Text | DOI | PubMed
- Lancet. 2014; 383:257-66. Publisher Full Text | DOI | PubMed
- Stat Med. 1996; 15:2733-49. Publisher Full Text | DOI | PubMed
- Stat Med. 2002; 21:589-624. Publisher Full Text | DOI | PubMed
- 2017 (in-press).
- J Clin Epidemiol. 2017; 82:20-8. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2016; 7:236-63. Publisher Full Text | DOI | PubMed
- BMJ. 2013; 346:f2914. Publisher Full Text | DOI | PubMed
- BMJ. 2011; 342:d549. Publisher Full Text | DOI | PubMed
- BMJ. 2005; 331:897-900. Publisher Full Text | DOI | PubMed
- Stat Med. 2011; 30:2502-3, discussion 2509-10. Publisher Full Text | DOI | PubMed
- Clin Trials. 2009; 6:16-27. Publisher Full Text | DOI | PubMed
- Stat Med. 2005; 24:2241-54. Publisher Full Text | DOI | PubMed
- Stat Med. 2009; 28:1218-37. Publisher Full Text | DOI | PubMed
- J Clin Epidemiol. 2016; 69:40-50. Publisher Full Text | DOI | PubMed
- Stat Med. 2015; 34:2481-96. Publisher Full Text | DOI | PubMed
- Stat Med. 2011; 30:2509-10. Publisher Full Text | DOI
- BMJ. 2013; 346:e8668. Publisher Full Text | DOI | PubMed
- Stata J. 2011; 11:255-70.
- Stat Med. 2012; 31:3821-39. Publisher Full Text | DOI | PubMed
- Stat Med. 2012; 31:3805-20. Publisher Full Text | DOI | PubMed
- Biom J. 2013; 55:231-45. Publisher Full Text | DOI | PubMed
- Biostatistics. 2008; 9:172-86. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2012; 3:80-97. Publisher Full Text | DOI | PubMed
- Stata J. 2015; 15:951-85.
- BMJ. 2011; 343:d4909. Publisher Full Text | DOI | PubMed
- Stat Methods Med Res. 2008; 17:279-301. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2012; 3:111-25. Publisher Full Text | DOI | PubMed
- 2013.
- BMC Med Res Methodol. 2015; 15:58. Publisher Full Text | DOI | PubMed
- Stat Med. 2004; 23:3105-24. Publisher Full Text | DOI | PubMed
- Ann Intern Med. 2016; 164:666-73. Publisher Full Text | DOI | PubMed
- PLoS One. 2013; 8:e76654. Publisher Full Text | DOI | PubMed
- J Clin Epidemiol. 2011; 64:163-71. Publisher Full Text | DOI | PubMed
- Stat Methods Med Res. 2017. DOI
- Stat Med. 2012; 31:2179-95. Publisher Full Text | DOI | PubMed
- Stat Med. 2014; 33:1441-59. Publisher Full Text | DOI | PubMed
- Stat Med. 2007; 26:78-97. Publisher Full Text | DOI | PubMed
- Stat Med. 2015; 34:3842-65. Publisher Full Text | DOI | PubMed
- Stat Methods Med Res. 2013; 22:169-89. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2015; 6:157-74. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2007; 7:3. Publisher Full Text | DOI | PubMed
- Stat Med. 2013; 32:1191-205. Publisher Full Text | DOI | PubMed
- Stat Med. 2013; 32:3926-43. Publisher Full Text | DOI | PubMed
- Stat Med. 2013; 32:2911-34. Publisher Full Text | DOI | PubMed
- Int J Epidemiol. 2012; 41:818-27. Publisher Full Text | DOI | PubMed
- Covey SR. The 7 Habits of Highly Effective People Personal Workbook: Simon & Schuster UK 2008.
- Stat Sci. 2013; 28:257-68. DOI
- BMC Med Res Methodol. 2003; 3:17. Publisher Full Text | DOI | PubMed
- Curr Control Trials Cardiovasc Med. 2000; 1:76-8. Publisher Full Text | DOI | PubMed
- BMJ. 2010; 340:c365. Publisher Full Text | DOI | PubMed
- PLoS Med. 2014; 11:e1001666. Publisher Full Text | DOI | PubMed
- Ann Intern Med. 2013; 159:130-7. Publisher Full Text | DOI | PubMed
- Value Health. 2014; 17:157-73. Publisher Full Text | DOI | PubMed
- Int J Epidemiol. 2013; 42:332-45. Publisher Full Text | DOI | PubMed
- BMC Med. 2013; 11:159. Publisher Full Text | DOI | PubMed
- Stat Med. 2013; 32:914-30. Publisher Full Text | DOI | PubMed
- Stat Methods Med Res. 2016;962280216660741. Publisher Full Text
- J Clin Epidemiol. 2009; 62:857-64. Publisher Full Text | DOI | PubMed
- PLoS One. 2014; 9:e86754. Publisher Full Text | DOI | PubMed
- Med Decis Making. 2013; 33:641-56. Publisher Full Text | DOI | PubMed
- Stat Med. 2010; 29:932-44. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2012; 3:98-110. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2016; 16:87. Publisher Full Text | DOI | PubMed
- Stat Med. 2016; 35:819-39. Publisher Full Text | DOI | PubMed
- Stat Med. 2014; 33:3639-54. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2014; 14:106. Publisher Full Text | DOI | PubMed
- Stat Med. 2014; 33:2275-87. Publisher Full Text | DOI | PubMed
- Biostatistics. 2015; 16:84-97. Publisher Full Text | DOI | PubMed
- Med Decis Making. 2013; 33:702-14. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2016; 7:6-22. Publisher Full Text | DOI | PubMed
- 2017.
- Stat Med. 2013; 32:25-39. Publisher Full Text | DOI | PubMed
- Value Health. 2015; 18:116-26. Publisher Full Text | DOI | PubMed
- BMJ. 2010; 340:c221. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2015; 15:34. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2016; 16:131. Publisher Full Text | DOI | PubMed
- BMC Med Res Methodol. 2014; 14:105. Publisher Full Text | DOI | PubMed
- Res Synth Methods. 2012; 3:177-90. Publisher Full Text | DOI | PubMed
- Stat Med. 2015; 34:2794-819. Publisher Full Text | DOI | PubMed
- Stat Med. 2016; 35:2485-502. Publisher Full Text | DOI | PubMed
- Value Health. 2014; 17:A576. Publisher Full Text | DOI
- Stat Med. 2017; 36:1210-26. Publisher Full Text | DOI | PubMed
- BMC Med. 2016; 14:8. Publisher Full Text | DOI | PubMed
- Lancet Oncol. 2016; 17:243-56. Publisher Full Text | DOI | PubMed
- PLoS One. 2014; 9:e99682. Publisher Full Text | DOI | PubMed
- Ann Intern Med. 2015; 162:777-84. Publisher Full Text | DOI | PubMed
- J Health Serv Res Policy. 2012; 17:1-2. Publisher Full Text | DOI
- J Clin Epidemiol. 2014; 67:138-43. Publisher Full Text | DOI | PubMed
Fonte
Riley RD, Jackson D, Salanti G, Burke DL, Price M, et al. (2017) Multivariate and network meta-analysis of multiple outcomes and multiple treatments: rationale, concepts, and examples. The BMJ 358j3932. https://doi.org/10.1136/bmj.j3932





