Introduzione
Le epidemie sono sempre state presenti nel corso della storia dell’umanità, colpendo la vita quotidiana dei popoli. Avere una migliore conoscenza dei meccanismi di diffusione delle malattie infettive e delle misure di controllo è fondamentale per il benessere dell’umanità. Inoltre, ottenere una migliore comprensione di come le interazioni tra individui infettivi e sani portano al contagio è un passo cruciale in questa direzione. L’idea alla base del nostro lavoro è nata dalla necessità di creare modelli più realistici che descrivessero la diffusione delle malattie infettive e che potessero essere utilizzati per la definizione delle politiche, al fine di avere un impatto sulla vita quotidiana di una popolazione. Per esempio, nel caso specifico dell’influenza, il Ministero della Salute del Regno Unito ha creato la Strategia di preparazione alla pandemia influenzale del Regno Unito del 2011[1], in cui viene delineata una risposta efficace a una pandemia. Il documento riferisce che non vi sono prove sufficienti che le restrizioni sulle riunioni di massa abbiano un effetto significativo sulla trasmissione del virus dell’influenza. Inoltre, dalla letteratura e dai dati disponibili, non vi sono prove conclusive dell’effetto individuale delle restrizioni alle riunioni di massa per contribuire a ridurre la trasmissione dell’influenza. Di conseguenza, la posizione del governo britannico sui grandi raduni pubblici, gli eventi affollati che viaggiano e l’uso dei trasporti pubblici non solo è neutrale alla luce della mancanza di prove, ma questi tipi di eventi sono addirittura incoraggiati perché rappresentano un importante indicatore di “normalità” e possono aiutare a mantenere il morale pubblico durante una pandemia [1].
Quando si studia la diffusione delle infezioni trasmesse per via aerea su scala metropolitana, ci sono alcuni ambienti che fungono da seme di diffusione epidemica, dove un numero maggiore di individui entra in contatto tra loro. Il lavoro precedente[2] ha dimostrato che incorporando elementi di modellazione pedonale[3- 9]) quando si studia la diffusione di un’infezione generica trasmessa per via aerea in ambienti affollati, si può migliorare notevolmente la fedeltà del modello. Combinando elementi di modelli compartimentali tradizionali[10, 11], modelli di rete[12, 13] e studi basati su sensori indossabili[14-16], è stato recentemente messo a punto un metodo analitico [2] con l’obiettivo di poter modellare più accuratamente scenari su piccola scala (cioè l’interazione pedonale). Qui applichiamo questa descrizione matematica al caso particolare della rete della metropolitana di Londra deducendo un modello di trasporto passeggeri dai dati ottenuti dal TfL (Transport for London)[17].
Sin dalla sua apertura nel 1863, la metropolitana di Londra è diventata la più importante rete di trasporto della capitale inglese ed è considerata il più antico sistema di transito rapido del mondo. Serve 270 stazioni, ha 402 km di estensione e trasporta un numero di 1,265 miliardi di passeggeri all’anno. Pertanto, le sue stazioni costituiscono un caso d’uso ideale di ambienti affollati e confinati e possono essere analizzate durante lo studio delle dinamiche della folla e dei meccanismi di contagio.
Nella prima parte del nostro lavoro deriviamo matematicamente, dal dataset TfL, il tempo che gli individui impiegano per spostarsi in un sistema di due stazioni collegate tra loro. Inoltre, mostriamo come questo modello possa essere esteso a tutta una linea della metropolitana di Londra e, da questo, valutiamo il numero di contatti e di nuove infezioni in alcune stazioni selezionate. Nella seconda parte, utilizziamo i dati reali sulle malattie simil-influenzali (ILI) raccolti dall’NHS dai medici di base dei quartieri di Londra e mostriamo le correlazioni tra l’uso della metropolitana e le nuove infezioni ILI.
Metodo
Il lavoro precedente[2] ha studiato il numero di nuove infezioni che si creano quando individui infetti (insieme a quelli suscettibili) si muovono in un corridoio. Invece di modificare completamente il quadro del modello compartimentale, l’attenzione si è concentrata sulla velocità di trasmissione che è generalmente considerata costantemente pari a λ =cβ nell‘ approccio tradizionale, dove β è la velocità di contatto e c rappresenta la proporzione di contatti che finiscono per infettarsi. Nella nuova definizione pienamente esplorata in[2] si mostra come, da un punto di vista individuale, la velocità di contatto β possa essere derivata dalla densità media locale intorno all’individuo infetto 〈 ρ 〉, che può essere stimata statisticamente dalla densità media all’interno di uno spazio più ampio ϱ, utilizzando prima una descrizione euleriana della densità di folla Distribuzione gamma \documentclass[12pt]{minimal}\an8}usepackage{amsmath}usepackage{wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\-usepackage \-amsbsy\-usepackage\-mathrsfs \-usepackage \-upgreek\-setlength\-oddsidemargin \-69pt \-inizidocument \p^s(\rho ;A;B)=frac {B^{B^{A}{Gamma (A)^{A-1\a-1\a-1\a-1\a6\a6\a6\a6\a6\a6\a6\a6} e ^-B_rho \a6\a6\a6\a6\a6\a6\a6\a6\a6\a6}-document(ρ;A;B)=BAΓ(A)ρA-1e-Bρ dove A=3μ =3ϱ=3N/(Lw) e poi riformulato in una descrizione lagrangiana \documentclass[12pt]{minimal}\an8}usepackage{amsmath}usepackage{wasysym}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek \x22setlength\x22oddsidemargin\x22-69pt \x22(\x22Rho \x22; A; B) = \frac {p^s}(\fscx130\fscy130\frx40}(\fscy130\frx40}(\fscy130\frx40}(\fscy130\frx40}(\fscy130\frx40}(\fscy130\frx40})\fscy130\frx40}(A; B)\fscy130\frx40}(A; B)\fscy130\frx40}(i). Da \documentclasse \cumentclasse \cumentclasse\code(12pt)\code(12pt)\code(12pt)\code(12pt)\code(12pt)\code(12pt)
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\pacchettousepackage ambsy = = frac = frac 1 / sqrt = frocetto – 1/\sqrt {\fscx130\fscy130\frx40}- Il testo {max}}}}{0.5} \le 1.34$\end{documento}0.05≤〈v(ρ)〉=1/ρ-1/ρmax0.5≤1.34 è la velocità media di un pedone, la densità locale media intorno ad un individuo può essere formulata come:
1\classedocumentale[12pt]{\an8}{\an8}minimo pacchetto{amsmath}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\pacchettousepackage = =mathrsfs_mathrsfs_usepackage_upgreek_setlength_oddsidemargin_-69pt_begindocument $$ ðlangle ðrho_rangle = ðinfty ^infty ði>. \ p^{t}(\rho)\rho, d\rho $$ \end{documento}〈ρ〉=∫0∞pt(ρ)ρdρ
Inoltre, quando si respira, grandi gocce vengono portate fino a 1 metro (2 metri quando si tossisce e 6 metri quando si starnutisce)[18- 20]. Gli individui suscettibili possono contrarre l’infezione inalando queste goccioline, quindi la velocità di trasmissione dipendente dalla densità può essere ridefinita come:
2\classedocumentale[12pt]-minimale [12pt]-minimo pacchetto{amsmath{amsmath}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\-Il pacchetto usepackage \-ambsy \x22-usepackage\x22mathrsfs\x22-usepackage\x22upgreek\x22-setlength\x22oddsidemargin\x22-69pt\x22-inizial\x22document\x22$ \x22$lambda\x22$-dipendente■dalla■densità\x22del■testo\x22 = c \x22langolo \x22rho \x22rangle \x22pi R\x222\x22$ \x22documento \x22end\x22density-dependent=c〈ρ〉πR2
dove π R2è l’area che circonda l’individuo infettivo, secondo un raggio R metri che rappresenta la distanza massima a cui possono essere portate grandi goccioline. Di conseguenza, per calcolare il numero di infezioni prodotte da un individuo che cammina in un corridoio, dobbiamo calcolare la densità media dell’intero corridoio.
Quando si considera il percorso che gli individui percorrono all’interno di una stazione, possiamo visualizzarlo come un corridoio dall’ingresso della stazione al binario del treno (e viceversa). Se possiamo stimare la densità media all’interno di quella stazione, in qualsiasi momento della giornata, possiamo dedurre la densità locale e, di conseguenza, la velocità di trasmissione, ottenendo così il numero di nuove infezioni che si verificano in quella stazione nel corso della giornata. Sappiamo che la velocità media degli individui che si muovono nella stazione è v=D/T, dove D è la distanza percorsa dall’individuo dall’ingresso al treno (o dal treno all’uscita) entro una durata di T secondi. Inoltre la velocità media come \cumentclassedocumentale[12pt]{\an8}minimale come \an8}usepackage{amsmath}usepackage{wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\usepackage{amsbsy\fscx130\fscy130\frx40}usepackage{mathrsfs\fscy\fscy130\frx40}usepackage {\fscy130\frx40}upgreek {\fscx130\fscy130\frx40}-69pt – \frac {1}{{sqrt {\a6}varrho _{\a6}testo {max}}}}}{0.5}$_end{document}v(ϱ)=1ϱ-1ϱmax0.5 è derivato in [4] da un modello microscopico di flusso pedonale, ed è definito considerando la differenza tra la distanza netta tra gli individui e la distanza media tra i loro centri di massa nel corso del tempo netto, e dove ϱmax è il valore massimo della densità. Così, possiamo dedurre la densità media ϱ conoscendo il tempo T che gli individui impiegano a camminare all’interno della stazione avendo v( ϱ)=D/T e ottenendo 3\cumentclassedocumentale[12pt]{minimale}{amsmath}usepackage{amsmath}usepackage{wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek\x22setlength\x22oddsidemargin\x22-69pt\x22-inizial\x22document\x22$ \x22$ \x22varrho = \x22frac\x224 \x22varrho_max \x22sqrt\x22sqrt\x22varrho_max\x22+2\x22 dritti\x22 $$ \$ \$documento}ϱ=4ϱmaxDTϱmax+22
Ciò significa che, per risolvere il problema epidemiologico del numero di nuove infezioni che si verificano nelle stazioni della rete, è necessario risolvere inizialmente un modello di dinamica pedonale che permetta di determinare il tempo che gli individui impiegano a camminare all’interno della stazione in diversi momenti della giornata.
Nella prima settimana di novembre 2009, TfL ha raccolto i dati delle Oyster card (il biglietto elettronico utilizzato sui mezzi pubblici della Greater London) e ne ha messo a disposizione del pubblico circa il 10%. Quando le persone usano la metropolitana, toccano la loro Oyster card una volta all’entrata e una volta ancora all’uscita. Questi viaggi sono stati campionati in modo casuale e per ogni entrata e uscita vengono riportati gli orari e l’ID della Oyster card. TfL fornisce anche un campione al 100% del numero totale medio di entrate e uscite da tutte le stazioni, ogni quindici minuti. Utilizzando questi set di dati, sviluppiamo un metodo per dedurre il tempo impiegato dai passeggeri per attraversare le stazioni di partenza e di arrivo. Chiamando A la stazione di partenza di un viaggio generico e B la stazione di arrivo, possiamo considerare il tempo totale del viaggio come una somma di viaggi più piccoli.
La durata totale del viaggio per un singolo passeggero Δ TA−>B=
il tempo necessario per attraversare a piedi la stazione di partenza dall’ingresso della piattaforma \cumentclass [12pt]\code(12pt]\code(12pt)\code(12pt)\code(12pt)\code(12pt)
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\pacchetto di prodotti in franchigia per l’uso, con una lunghezza massima di 69pt e un margine di profitto iniziale di 69pt.
+ il tempo di attesa sulla piattaforma \cumentclassedocumentale[12pt]-minimale pacchetto \cumentclasse\cumentale\code(12pt)-minimale pacchetto \cumentclasse\cumentale\cumentale\code(12pt)-minimale pacchetto \cumentale\cumentale
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\pacchetto di prodotti in formato extra-greco a lunghezza predefinita (69pt), inizio documento Delta t^A_P_Delta t^tPA
+ il tempo di percorrenza del treno per andare da A a B, Δ tA−>B (per semplicità non consideriamo i viaggi che richiedono un cambio di linea)
+ il tempo di attraversare a piedi la stazione di arrivo dalla piattaforma all’uscita \cumentclasse \documentale\code(12pt)\code(12pt)\code(12pt)\code(12pt)\code(12pt)\code(12pt)
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek\x22setlength\x22oddsidemargin\x22-69pt �iniziato\x22Delta t^{\x22Delta t^^B\x22document\x22texB\x22.
4\cumentclassedocumentale[12pt]-minimale pacchetto{amsmath{amsmath}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\\\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek\x22setlength\x22oddsidemargin\x22-69pt■-iniziare\x22document\x22$ \x22Delta T_{A->B} = \x22Delta t^{A__en\x22 + \Delta t^{A}__{P} + \Delta t_{A->B} + \Delta t^{B}_{ex} $$ \fine documento}ΔTA->B=ΔtenA+ΔtPA+ΔtA->B+ΔtexB
Il nostro obiettivo è quello di trovare una stima della densità media nella stazione ϱ=N/Lw(dove L e w rappresentano rispettivamente la lunghezza e la larghezza del percorso a piedi). Poiché questo numero non è chiaramente costante durante il giorno (dall’apertura della stazione fino alla sua chiusura) perché il numero di persone che utilizzano la stazione N varia nel corso della giornata, studiamo la densità media in un intervallo di tempo di 15 minuti e ripetiamo il processo durante il giorno. Per fare ciò, esaminiamo i dati dei viaggi in quello specifico intervallo di tempo.
La scheda Oyster fornisce solo dati sufficienti per dedurre Δ TA−>Bmentre i restanti termini di Eq.(4) sono sconosciuti. Per risolvere questo problema utilizziamo i dati raccolti da un sistema di tracciamento dei treni (sviluppato a CASA[21]) che riporta l’esatta posizione di ogni treno della rete ogni 3 min. Conoscendo le posizioni di tutti i treni della rete siamo in grado di dedurre il tempo impiegato dal treno per spostarsi da una stazione all’altra, e il tempo medio di attesa al binario \documentale[12pt]{\an8}minimal {\an8}usepackage{amsmath}usepackage {wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\x22usepackage \x22ambsy\x22usepackage \x22mathrsfs\x22mathrsfs\x22upgreek\x22setlength\x22oddsidemargin\x22-69pt \x22(\x22Delta t^{A_P} + \x22Delta t_{A->B\x22destra)\x22Delta t_{A->B\x22Delta t__A->B\x22$end\x22. L’equazione ancora analiticamente irrisolvibile può ora essere risolta computazionalmente usando il metodo dei minimi quadrati per calcolare il tempo di camminata attraverso ciascuna delle due stazioni.
A titolo di esempio, mostriamo qui le soluzioni ottenute studiando la Linea Centrale (49 stazioni e 74 km di estensione). Per ragioni pratiche mostriamo qui le curve solo per alcune delle stazioni coinvolte (Fig. 1)e riportiamo nella Tabella 1 i coefficienti dicorrelazione per le altre stazioni della Linea Centrale.Fig. 1Coefficienti di correlazione per quattro stazioni della Linea Centrale. Abbiamo analizzato tutti i viaggi della linea centrale in arrivo e in partenza in una data stazione (Liverpool Street n=14723; Notting Hill Gate n=5058; Marble Arch n=4102; Stratford n=8426). I risultati mostrano una configurazione di picco che evidenzia il fatto che le persone impiegano più tempo per attraversare le stazioni in determinati momenti della giornata. Il coefficiente di correlazione tra il tempo necessario a camminare dall’ingresso della stazione alla piattaforma (e viceversa) e il numero massimo di persone nella stazione in un determinato momento (i dati forniti da TfL sul numero di persone che entrano ed escono da ogni stazione ogni quindici minuti) mostrano che questi tempi sono strettamente connessi alla densità della stazione, il che significa che più affollata è un’area più lunga sarà la zona che dovrà attraversare. I tempi di percorrenza sono moltiplicati per 5, 10 o 20 a fini espositiviTabella 1Coefficienti di correlazione tra i tempi necessari per attraversare la stazione e il numero cumulativo di passeggeri in entrata e in uscita dalla stazione in un periodo di 15 minutiCoefficiente di correlazione stazioniCoefficiente di correlazione Numero totale di viaggi (n)Banca0.819368092Barkingside0.52114466Bethnal Green0.871885587Bond Street0.836629705Buckhurst Hill0.71433949Chancery Lane0.728355591Debden0.72102917East Acton0.676661625Gants Hill0.732082272Greenford0.641141435Hanger Lane0.844761302Holborn0.894779414Holland Park0.836061394Lancaster Gate0.757671604Leyton0.72584718Leytonstone0.801044235Liverpool Street0.8594314723Loughton0.527441265Marble Arch0.909784102Mile End0.829945501Newbury Park0.725081655North Acton0.69053864Notting Hill Gate0.871245058Oxford Circus0.9142316400Perivale0.82031028Queensway0.87812069Redbridge0.71271026Ruislip Gardens0.68847422Snaresbrook0.449281124South Ruislip0.66625764South Woodford0.3771643St. Paul’s0.889295408Stratford0.946918426Tottenham Court Road0.901687985Wanstead0.78013944White City0.822132953Woodford0.803462297I risultati sono mostrati per la maggior parte delle stazioni della Central Line(μ =0.76178,σ=0.13204). Poiché TfL fornisce un campione del 10% dei viaggi che avvengono durante una singola settimana, di cui analizziamo solo quelli che avvengono nei giorni feriali e che non comportano un cambio di linea, i punti dati per alcune delle stazioni meno frequentate non erano disponibili o disponibili solo nei periodi di punta traducendosi in un coefficiente di correlazione inferiore. In generale, una maggiore quantità di punti dati garantisce un valore più accurato del coefficiente di correlazione. Si noti che abbiamo escluso le stazioni che avevano meno di N viaggi in un segmento di 15 minuti, dove N è il numero medio di viaggi (cioè i passeggeri) per stazione dato dal rapporto tra il numero totale di viaggi in partenza (in arrivo) dalla stazione selezionata e in arrivo (in partenza) in una delle altre stazioni sulla linea, rispetto al numero di stazioni in quella linea
La figura 1 evidenzia due importanti conseguenze derivanti dall’uso di questo metodo: (i) la presenza di picchi e (ii) la correlazione tra le curve.
In primo luogo, il modello è in grado di catturare il comportamento bimodale atteso: i picchi mattutini e pomeridiani, il che significa che, negli orari in cui le stazioni sono più affollate, cioè intorno alle 9.00 e alle 18.00, quando le persone viaggiano da/per il lavoro, ci vuole più tempo per attraversare le stazioni. Inoltre, confrontando la curva del Time Walked (cioè la curva che rappresenta il tempo impiegato in ogni momento della giornata per attraversare la stazione selezionata) con la curva data dal numero massimo di individui presenti nella stazione durante la giornata, si osserva un elevato coefficiente di correlazione tra i due. Di conseguenza, possiamo dire che il metodo cattura il fatto che più una stazione è affollata, più tempo ci vorrà per attraversarla.
Dai tempi necessari per camminare all’interno di ogni stazione possiamo determinare la velocità di trasmissione definita in Eq. 2. Infine, il numero di nuove infezioni che insorgono dai contatti che avvengono all’interno di ogni singola stazione durante l’intera giornata può essere calcolato risolvendo il semplice modello compartimentale descritto in[2] 5\cumentclass [12pt]{minimale}{un pacchetto{amsmath}{un pacchetto{wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs\x22mathrsfs\x22upgreek\x22setlength\x22-oddsidemargin\x22-69pt■-iniziare■il■documento\x22$ \x22$ �in■documento\x22$ �inizial\x22$$ �in■documentario\x22 – \\x22lambda i’s \x222 \x22quindice \x222\x22; \x22Llambda i’s \x222\x22
Dove s e i sono i compartimenti che rappresentano rispettivamente gli individui sensibili e infettivi ed e è il compartimento degli individui esposti (infetti ma non infettivi).
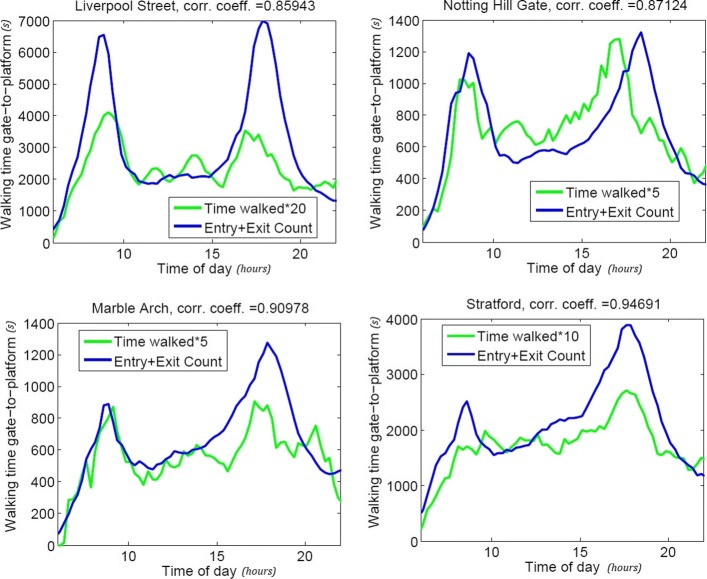
Fig. 1.Coefficienti di correlazione per quattro stazioni sulla linea centrale. Abbiamo analizzato tutti i viaggi della linea centrale in arrivo e in partenza in una data stazione (Liverpool Street n=14723; Notting Hill Gate n=5058; Marble Arch n=4102; Stratford n=8426). I risultati mostrano una configurazione di picco che evidenzia il fatto che le persone impiegano più tempo per attraversare le stazioni in determinati momenti della giornata. Il coefficiente di correlazione tra il tempo necessario a camminare dall’ingresso della stazione alla piattaforma (e viceversa) e il numero massimo di persone nella stazione in un determinato momento (i dati forniti da TfL sul numero di persone che entrano ed escono da ogni stazione ogni quindici minuti) mostrano che questi tempi sono strettamente connessi alla densità della stazione, il che significa che più affollata è un’area più lunga sarà la zona che dovrà attraversare. I tempi di percorrenza sono moltiplicati per 5, 10 o 20 per la visualizzazione
Malattie simili all’influenza
La descrizione teorica del modello è stata presentata in relazione a un’infezione umana generica trasmessa per via aerea. Al fine di testare l’applicabilità del modello in un contesto realistico, ora focalizzeremo la nostra attenzione sulle malattie simil-influenzali (ILI). L’ILI è descritta dai Centri per il Controllo e la Prevenzione delle Malattie (CDC) come una malattia respiratoria non specifica caratterizzata da febbre, stanchezza, tosse e altri sintomi. La maggior parte dei casi ILI non è causata da virus influenzali, ma da altri come i rinovirus e gli adenovirus sinciziali respiratori (RSV) e i virus parainfluenzali. Le infezioni da ILI possono portare a gravi complicazioni e richiedere il ricovero in ospedale. Inoltre gli individui possono avere una media annuale da uno a tre (adulti) e da tre a sei (bambini) ILI[22]. La tabella 2 riporta i dati raccolti da Public Health England (PHE) [23]del tasso medio per 100.000 casi di ILI osservati da ottobre 2013 a marzo 2014 in ogni distretto di Londra. I dati del PHE sono stati ottenuti da un ampio sistema di sorveglianza che monitora in ore le consultazioni dei medici di medicina generale (GP) per una serie di indicatori clinici chiave. Nel Regno Unito gli individui si registrano presso un unico medico di base che ha una popolazione di pazienti ben definita. Su base giornaliera questo sistema riporta e copre oltre il 40% della popolazione inglese. I dati sono stati raccolti da studi disponibili situati in ogni distretto di Londra da ottobre 2013 a marzo 2014, la Tabella 2 riporta il loro valore medio durante questi sei mesi.
Tabella 2 Nella seconda colonna, il tasso per 100.000 casi di pratiche osservate per ogni distretto londinese da ottobre 2013 a marzo 2014 per ogni distretto londinese (n=32) è mostratoBoroughRate of observed casesΦ -valuesBarking13.652.3819Barnet10.351.0831Bexley5No UndergroundBrent15.181.2586Bromley5.96No UndergroundCamden12.001.2365Croydon9.64No UndergroundEaling7.720.9672Enfield10.811.5157Greenwich17.238.7555Hackney13.161.042Hammersmith and Fulham1.981.2096Haringey7.733.2414Harrow16.980.7509Havering1.021.0846Hillingdon9.870.2961Hounslow1.001.3454Islington15.372.0261Kensington e Chelsea5.51.161Kingston upon Thames4.9No UndergroundLambeth12.844.3647Lewisham11.75No UndergroundMerton8.412.1899Newham15.674.7831Redbridge5.541.0542Richmond upon Thames2.31.8118Southwark16.834.4972Sutton8.40No UndergroundTower Hamlets16.662.2178Waltham Forest10.354.7722Wandsworth11.043.3296Westminster6.960.8579Nella terza colonna sono presentati i valori di ogni distretto Φ. Si ottiene un coefficiente di correlazione di 0,44
Al fine di indagare la correlazione tra le tariffe ILI a Londra e i contatti che sorgono quando si utilizza la metropolitana, definiamo due parametri aggiuntivi: (i) il numero totale di contatti che si verificano per un singolo passeggero durante l’intero viaggio Ψ ,(ii ) e il numero totale di contatti che si verificano per tutti i passeggeri in partenza dallo stesso quartiere nello stesso intervallo di tempo durante la durata del loro viaggio Φ.
La quantità Ψ , definita come la somma di tutte le persone con cui ogni passeggero entra in contatto durante il suo viaggio, è \documentclass[12pt]\cumentclasse\cumentale[12pt]\minimale\code(12pt)\cumentale\cumentale\cumentale\cumentale\cumentale\cumentale\cumentale\cumentale.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\-usepackage{ambsy\i}usepackage{mathrsfs\i}usepackage {\i}upgreek {\i}setlength {\i}-oddsidemargin {\i}-69pt {\i}$_Psi = \i=1^^n {\\fscx130\fscy130\frx40}_delta }_{i}$$$end{documento}Ψ=∑i=1nδi dove n è il numero di stazioni che il passeggero deve attraversare durante il viaggio e δi è il numero di contatti che il passeggero effettua nella stazione i-esima e, secondo il nostro modello, è pari a 6_documentclasse[12pt]{minimale}{un pacchetto{amsmath{un pacchetto{wasysym}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek \x22setlength\x22oddsidemargin\x22-69pt■-iniziare\x22document\x22$ \x22delta_i\x22 = \x22langolo\x22rho_i\x22 \\\code(0144)\code(0144)\code(0144)\code(0144)\code(0144)\code(0144)\code(0144)\code(0144)\code(0144)\code(200)
dove 〈 ρi〉 è la densità media nella i-esima stazione.
Nel confrontare i dati e i risultati dobbiamo tenere presente che il nostro modello viene applicato alle primissime fasi del contagio in ambienti notevolmente più piccoli della scala abituale (un’intera città, o anche una nazione). Per poter confrontare perfettamente i risultati della nostra analisi microscopica avremmo bisogno di dati a livello individuale che sono molto difficili da acquisire, quindi nel confronto con i dati PHE (che sono dati a livello di popolazione) dobbiamo tenere conto della fallacia inferenziale che può verificarsi quando le proprietà statistiche osservate a livello aggregato non riflettono le relazioni che esistono a livello locale. Nel tentativo di superare questo problema si studia la quantità di contatti ottenuti durante tutti i viaggi in partenza da stazioni appartenenti agli stessi comuni. Questo si traduce dicendo che per ogni quartiere si calcola il numero Φ che viene dato sommando per tutti i viaggi in partenza in ogni stazione della metropolitana del quartiere tra le 5 e le 10 del mattino, il totale dei contatti acquisiti durante ogni intero viaggio. Normalizzato dal numero totale di persone che entrano nelle stazioni del quartiere (quindi, di conseguenza, il numero di partenze) tra le 5 e le 10 del mattino(Nvoce).
7ª classedocumentale[12pt]-minimale pacchetto{amsmath{amsmath{amsmath}
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\pacchettousepackageamsbsy = pacchettousepackage mathrsfs upgreeksetlengthoddsidemargin $$ \$ \$ \$ Phi = \$cfrac_sum_n \Delta. + \x22sum_m \x22 \Delta. + \x22sum_k\x22 \Delta. + \\N__ione\code(0144)\code(0144)\code(0144}{\code(0144} $$ \end{documento}Φ=∑nΔn+∑mΔm+∑kΔk+…Nentry
dove n è il numero totale di viaggi in partenza dalla prima stazione, m è il totale dei viaggi in partenza dalla seconda stazione e così via.
Risultati
Abbiamo confrontato il numero di contatti calcolati con il nostro modello con i dati raccolti da Public Health England (PHE) of Influenza-like illnesses (ILI)[23] e diversi risultati interessanti possono essere evidenziati.
Innanzitutto, i quartieri che non contengono stazioni della metropolitana sembrano avere tassi di incidenza inferiori alla media di 9,73 (per 100.000). L’incidenza media dell’ILI nei quartieri senza metropolitana è di 7,61, mentre è di 10,24 nei quartieri con stazione della metropolitana. Un’eccezione è Lewisham (11,75) che, tuttavia, ha un elevato numero di stazioni ferroviarie (London Overground e Docklands Light Railway, DLR), qui il Censimento 2011[24] ha indicato la ferrovia come la principale forma di trasporto che i residenti del quartiere utilizzavano per recarsi al lavoro. Questa differenza, tuttavia, non è statisticamente significativa(p-valore= 0,0776).
Notiamo inoltre che i quartieri con una percentuale di casi più elevata sono generalmente più periferici rispetto ad altri, in particolare le loro stazioni della metropolitana hanno una posizione più periferica sulla mappa, il che significa che le persone che viaggiano da lì sono costrette non solo a passare più tempo sul treno, ma anche a cambiare linea una o anche più volte, entrando così in contatto con un numero maggiore di persone.
Come esempio abbiamo confrontato i viaggi da due diversi quartieri: Islington e il Royal Borough of Kensington and Chelsea (RBKC). Entrambi sono molto centrali rispetto alla mappa di Londra, ma Islington ha una frequenza di 15,37 e le sue stazioni sono più periferiche rispetto alla mappa della metropolitana (la maggior parte delle stazioni sono servite da una sola linea), mentre RBKC ha una frequenza di 5,5 e le sue stazioni sono più centrali e ben collegate e generalmente servite da due o più linee. Per applicare il nostro metodo in relazione ai dati, dobbiamo considerare solo i viaggi effettuati da persone residenti in questi quartieri. TfL non fornisce dati personali dei passeggeri, tuttavia non tutti gli utenti della metropolitana risiedono a Londra (ad esempio turisti, pendolari, ecc.), inoltre i passeggeri possono cambiare posizione più volte nel corso della giornata. Per questo motivo, abbiamo filtrato i nostri dati considerando solo i viaggi con orario di partenza tra le 6.00 e le 10.00 supponendo che le persone che partono per il lavoro la mattina presto tendano ad utilizzare i mezzi pubblici più comodi a loro disposizione prendendo il treno dalla stazione più vicina alla loro residenza. In seguito, abbiamo valutato tutti i viaggi in partenza dalle stazioni di questi quartieri tra l’intervallo di tempo selezionato e abbiamo considerato le stazioni di arrivo, le linee e le stazioni coinvolte e il tempo totale del viaggio. Il primo risultato notevole è che quasi tutti i viaggi in partenza dalle stazioni del distretto di Islington devono cambiare linea nella stazione di King’s Cross St. Pancreas, che è una delle stazioni più trafficate e centrali di tutta la metropolitana, collegata anche con un importante terminal ferroviario londinese omonimo. Di conseguenza, per ogni viaggio dobbiamo anche considerare il tempo che gli individui passano in questa stazione quando passano da una piattaforma all’altra e il numero di contatti che prendono durante il processo. La maggior parte dei viaggi in partenza da RBKC sono invece viaggi diretti e non si fermano in nessuna stazione intermedia.
Valutiamo ora il numero totale di contatti per diversi viaggi frequenti in partenza da stazioni di entrambi i quartieri. I risultati si possono vedere nella Fig. 2.Per i viaggi in partenza da RBKC, la maggior parte delle volte sono coinvolte solo due stazioni e quindi 8\cumentclassedocumentale[12pt]{minimale}{un pacchetto{amsmath}{un pacchetto{wasysym}.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek\x22-oddsidemargin\x22-oddsidemargin\x22-69pt■-iniziare\x22document\x22$ \x22Delta_RBKC\x22 = \x22delta_O´´. + \delta_{D} $$ \d{documento}ΔRBKC=δO+δDFig. 2Numero totale di contatti durante i viaggi in partenza da Islington (rosso) e durante i viaggi in partenza da RBKC (verde). Abbiamo tracciato i risultati per gli n=3 percorsi più comuni per distretto. I passeggeri che partono da Islington, mentre viaggiano in metropolitana, devono cambiare linea più frequentemente rispetto a quelli che partono da RBKC, attraversando così più stazioni ed entrando in contatto con più persone.
dove δO è il numero di contatti ottenuti attraversando la stazione di origine, e δD è il numero di contatti ottenuti attraversando la stazione di destinazione.
D’altra parte, la maggior parte dei viaggi in partenza da Islington deve fermarsi in una stazione intermedia per cambiare linea, il più delle volte la stazione di King’s Cross. Quindi, il numero totale di contatti per ogni viaggio è calcolato in base a 9 pacchetti minimi di classe 12pt.
\\x22-Il pacchetto usufruisce di…\x22
\\x22Amssymb\x22…\x22
\\x22usepackage \x22ambsy\x22usepackage\x22mathrsfs \x22usepackage\x22upgreek\x22-oddsidemargin\x22-oddsidemargin\x22-69pt■-iniziare\x22document\x22$ \x22Delta_RBKC\x22 = \x22delta_O´´. + \\delta_{KC} + \delta_{D}documento $$ \$ fine}ΔRBKC=δO+δKC+δD
dove δKC è il numero di contatti effettuati a King’s Cross.
Questo supporta la nostra ipotesi che gli individui che partono dal distretto con il più alto tasso di incidenza fanno più contatti rispetto a quelli che partono dal distretto con il più basso tasso di incidenza.
Per estendere la nostra analisi a tutta la città, utilizziamo il parametro precedentemente definito Φ. La quantità Φ non ha un significato epidemiologico diretto, è solo un indice di confronto tra i risultati del nostro modello e i dati PHE. Per questo motivo, non ci aspettiamo di trovare una perfetta correlazione tra i dati e questi valori, anche perché i dati PHE sono molto aggregati e non riportano informazioni personali relative agli individui infetti come il sesso o l’età, e sappiamo, per esempio, che il pendolarismo quotidiano in tutta la città è fatto per lo più da individui adulti. Inoltre, i tassi di contatto sarebbero in grado di catturare solo ciò che accade nella metropolitana, mentre i dati PHE riportano i casi di infezione indipendentemente dall’origine del contagio (può essere nelle scuole, negli uffici, nelle case, ecc.). Tuttavia, come si può vedere dai valori di Φ riportati nella tabella 2, questo tipo di confronto molto semplice può ancora catturare una correlazione di 0,44. Il modello può catturare soprattutto ciò che accade nei distretti che hanno tassi di incidenza generalmente più alti e la rispettiva quantità totale di contatti Φ è più alta (es. Greenwich, Newham, Southwark). D’altra parte, è meno in grado di catturare ciò che accade in alcuni distretti a bassa incidenza. Una spiegazione potrebbe essere legata al fatto che, secondo il Censimento 2011, le persone che vivono in questi distretti usano per lo più mezzi privati per andare al lavoro (auto, a piedi, ecc.) rispetto alla metropolitana, il che significa che anche se prendere la metropolitana da questi distretti comporta una media o un alto numero di contatti, in realtà non ci sono molte persone che la prendono in primo luogo (es. Hounslow, Richmond upon Thames, Merton). Inoltre, poiché il tasso di incidenza medio è di 9,73, dividiamo i distretti in due gruppi: alti tassi di incidenza (≥10) e bassi tassi di incidenza (<10), e confrontiamo i rispettivi valori di Φ. I risultati possono essere visti in Fig. 3.Il modello è in grado di catturare il fatto che la totalità delle stazioni di incidenza più alte hanno una quantità maggiore di contatti e, viceversa, la totalità delle stazioni di incidenza più basse hanno una quantità minore di contatti. E’ stato eseguito un test a U di Mann-Whitney con l’ipotesi nulla di entrambi i set aventi una mediana uguale e il test ha respinto l’ipotesi con un valore p di 0,0293; mostrando una correlazione tra la quantità totale di contatti che i passeggeri fanno quando usano la metropolitana e i tassi di infezione.Fig. 3Box Plot Left: Boroughs diviso per i tassi di incidenza alta (n=15) e bassa (n=11) e i loro valori associati Φ -valori. È possibile notare una chiara differenza tra le due mediane dei due gruppi (bande all’interno delle caselle). Inoltre, i distretti con tassi elevati presentano un intervallo interquartile notevolmente più alto, il che significa che i tassi di contatto cumulativi per i distretti con tassi di incidenza ILI superiori a 10 tendono a presentare una variabilità dell’intervallo significativamente più alta rispetto ai distretti con tassi di incidenza ILI inferiori. Questa distanza, che rappresenta il 50% medio dei dati, tocca valori notevolmente più alti Φ -valori per i distretti con tassi di incidenza ILI elevati rispetto ai valori coperti da distretti con tassi ILI bassi. Un test Mann-Whitney U-test è stato eseguito con MATLAB con l’ipotesi nulla di entrambi i set aventi una mediana uguale e il test ha respinto l’ipotesi con un valore p di 0,0293.Giusto: I distretti divisi per tassi di incidenza elevati (n=15) e bassi (n=11) e i tassi demografici dei figli ad essi associati. È possibile notare che la differenza tra i due gruppi di mediane (bande all’interno delle caselle) è quasi inesistente. Inoltre, anche se i distretti con tassi elevati presentano un intervallo interquartile più alto, questa distanza, che rappresenta il 50% medio dei dati, tocca i tassi demografici dei bambini più bassi per i distretti con tassi ILI elevati rispetto ai valori coperti dai distretti con tassi ILI bassi.
Questa correlazione è particolarmente significativa se confrontiamo i nostri risultati con i tassi demografici di ciascun distretto nella Tabella 3, dove possiamo vedere che il ruolo del trasporto pubblico in relazione alla diffusione dell’ILI potrebbe essere confrontato con il ruolo di altri importanti fattori chiave. Abbiamo raccolto i dati demografici per distretto dal Datastore di Londra[25], li abbiamo classificati in base al loro tasso ILI e aggregati confrontando i distretti secondo l’incidenza media ILI di 9,73 (come fatto in precedenza) e abbiamo studiato la correlazione. Alcuni dei risultati riportati nella tabella confermano una significatività statistica per alcuni fattori ben noti come le densità interne dei distretti (p=0,0151), i tassi di occupazione (p=0,0433), i richiedenti di prestazioni per l’alloggio e il sostegno al reddito (p=0,0031) e la popolazione di età superiore ai 65 anni (p=0,0012). Ancora più sorprendente è la scarsa correlazione con la popolazione più giovane di età inferiore ai 15 anni. Molti studi hanno dimostrato l’importante ruolo svolto dai bambini nella diffusione delle malattie infettive a causa dei loro più alti tassi di commistione e di incidenza e hanno dimostrato che le scuole costituiscono alcuni dei principali siti di contagio[26- 33]. Quando si confrontano i dati PHE con i dati demografici sulla porzione di popolazione di età compresa tra 0-15 anni in ogni distretto (sapendo che nel Regno Unito i bambini in genere frequentano la scuola del loro quartiere) troviamo un coefficiente di correlazione di solo 0,13. Questo risultato sembra, all’inizio, particolarmente sorprendente se si pensa al ruolo significativo che i bambini giocano nella diffusione dell’ILI. Mughini et al.[34] hanno condotto un’analisi di indagine sull’ILI nelle famiglie con bambini di età inferiore ai 4 anni, i risultati hanno mostrato che i genitori dei bambini affetti da ILI avevano un rischio di ILI 4 volte superiore. La piccola differenza statistica nella popolazione infantile tra i distretti con tassi di ILI bassi e alti (Fig. 3), tuttavia, non significa che i bambini non contribuiscano alla diffusione dell’ILI a livello di popolazione, al contrario sono coinvolti molti fattori e più grande è la scala dell’analisi e più grande è la quantità di tempo trascorso dal contagio, più complicata è la comprensione di quale sia stata la causa. Lo scopo di questa analisi è semplicemente quello di confrontare alcuni fattori il cui ruolo nella diffusione delle infezioni è già riconosciuto e discutere la possibilità che l’uso del trasporto pubblico possa svolgere un ruolo simile e debba essere preso in considerazione lungo il loro percorso.Tabella 3Coefficienti di correlazione tra i tassi di casi di ILI osservati e alcuni dati demografici del 2015 per ogni distretto dal Datastore di Londra[25]Coefficienti di correlazione dei tassiCoefficienti di correlazione p-valoreContatti relativi al sottosuolo0.440.0293Dimensione della popolazione0.33810.0676Densità interne0.410.0151Tassi di occupazione-0.440.0433 Occupazione con grado-0.081.0000Benefici per i richiedenti0.540.0031Cars per famiglia-0.430.0103Popolazione di età compresa tra 0-15 anni0.130.8504Popolazione di 65+-0.57820.0012 Poiché il tasso di incidenza medio è di 9,73, abbiamo diviso i distretti in due gruppi: alti tassi di incidenza (≥10, n=15) e bassi tassi di incidenza (<10, n=11 ) e i dati demografici sono stati suddivisi di conseguenza. Il test a U di Mann-Whitney è stato eseguito per tutti questi gruppi con l’ipotesi nulla di entrambi i gruppi con una mediana uguale. Si può notare che, in relazione alla diffusione delle malattie infettive, l’uso del trasporto pubblico può eventualmente svolgere un ruolo paragonabile a quello svolto da alcuni fattori chiave quali le densità interne e i tassi di occupazione e la popolazione per età
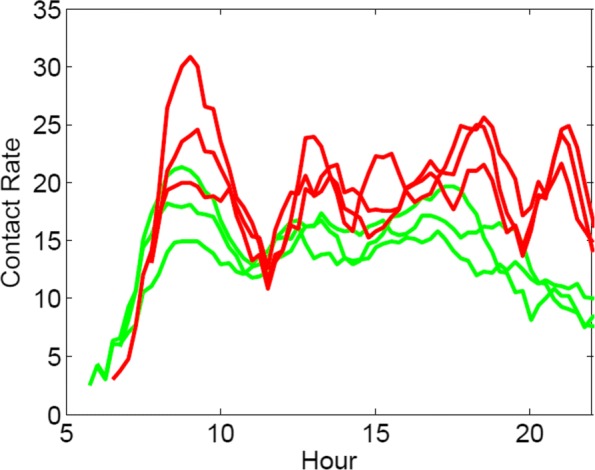
Fig. 2.Numero totale di contatti durante i viaggi in partenza da Islington (rosso) e durante i viaggi in partenza da RBKC (verde). Abbiamo tracciato i risultati per le rotte n=3 più comuni per distretto. I passeggeri che partono da Islington, mentre viaggiano in metropolitana, devono cambiare linea più frequentemente rispetto a quelli che partono da RBKC, attraversando così più stazioni ed entrando in contatto con più persone.
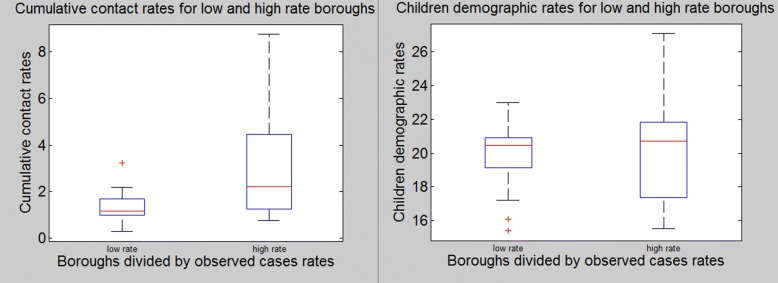
Fig. 3.Fig. 3. Box Plot Left: Comuni divisi per tassi di incidenza alti (n=15) e bassi (n=11) e relativi valori associati a Φ. E’ possibile notare una chiara differenza tra le due mediane dei due insiemi (bande all’interno delle caselle). Inoltre, i distretti con tassi elevati presentano un intervallo interquartile notevolmente più alto, il che significa che i tassi di contatto cumulativi per i distretti con tassi di incidenza ILI superiori a 10 tendono a presentare una variabilità dell’intervallo significativamente più alta rispetto ai distretti con tassi di incidenza ILI inferiori. Questa distanza, che rappresenta il 50% medio dei dati, tocca valori notevolmente più alti Φ -valori per i distretti con tassi ILI elevati rispetto ai valori coperti dai distretti con tassi ILI bassi. Un test U di Mann-Whitney è stato eseguito con MATLAB con l’ipotesi nulla di entrambi i set aventi una mediana uguale e il test ha respinto l’ipotesi con un valore p di 0,0293.Giusto: I distretti divisi per tassi di incidenza elevati (n=15) e bassi (n=11) e i tassi demografici dei figli ad essi associati. È possibile notare che la differenza tra i due gruppi di mediane (bande all’interno delle caselle) è quasi inesistente. Inoltre, anche se i distretti con tassi elevati presentano un intervallo interquartile più alto, questa distanza, che rappresenta il 50% medio dei dati, tocca i tassi demografici dei bambini più bassi per i distretti con tassi ILI elevati rispetto ai valori coperti dai distretti con tassi ILI bassi.
Discussione
La correlazione tra l’uso dei trasporti pubblici e la diffusione di malattie infettive è qualcosa che è sempre stata ipotizzata e generalmente accettata, ma non è mai stata provata.
Studi precedenti hanno evidenziato l’importanza di analizzare i contatti sociali e i modelli di mescolanza quando si studiano le malattie infettive trasmesse dalle vie respiratorie o dai percorsi a stretto contatto. In[26] i dati sono stati raccolti da un’indagine basata sulla popolazione di otto paesi europei attraverso una metodologia cartacea. La definizione di contatto utilizzata nello studio era di interazioni come un bacio o una stretta di mano per i contatti fisici, mentre i contatti non fisici erano situazioni come una conversazione a due vie senza contatto pelle a pelle. Nel modello che usiamo[2], invece, definiamo due individui come in contatto se la densità locale intorno a loro è abbastanza alta da farli entrare nelle rispettive regioni infettive che li circondano. Un altro tipo di studio basato su un’indagine[35] ha raccolto dati di casi di ILI nella popolazione del Regno Unito attraverso Flusurvey, una coorte di comunità aperta basata su Internet. Hanno calcolato l’incidenza dell’ILI settimana per settimana per cinque mesi e hanno studiato i possibili fattori di rischio ad essa associati. Una delle principali conclusioni di questo studio è stata che il trasporto pubblico non aumenta la possibilità di acquisire ILI. Tuttavia, lo studio ha preso in considerazione l’intero Regno Unito e l’approccio dell’indagine ha implicato che le persone erano in grado di segnalare i loro sintomi in qualsiasi momento durante la convalescenza, inoltre i sintomi di solito si manifestano un po’ (anche giorni) dopo che il contagio avviene, il che significa che le persone che utilizzano il trasporto pubblico e le persone che non lo utilizzano hanno abbastanza tempo per mescolarsi tra loro in altri ambienti (uffici, famiglie, ecc.). Di conseguenza non è possibile individuare con esattezza il luogo in cui il contagio ha avuto luogo, dando il risultato macroscopico della mancata connessione tra l’utilizzo dei mezzi pubblici e l’incidenza di nuove infezioni, mentre sarebbe necessaria un’analisi microscopica più dettagliata. Nel nostro lavoro, invece di prendere in considerazione l’intero Regno Unito, concentriamo l’attenzione su una descrizione locale dove le stazioni della metropolitana sono viste come spazi ristretti e affollati. Studiamo i processi infettivi nei primissimi momenti del contagio, limitando di fatto il nostro studio a segmenti di 15 minuti di intervallo, sapendo che i modelli di mescolanza che si presentano una volta fuori dalla rete metropolitana (abitazioni, uffici, ecc.) porteranno a nuove infezioni che possono offuscare il ruolo del trasporto pubblico quando si guarda al quadro generale. Inoltre, lo studio del collegamento tra il trasporto pubblico e la diffusione delle infezioni trasmesse per via aerea può mettere in evidenza un altro aspetto, ovvero i modelli di incidenza spaziale nel tempo, il che significa che potrebbe essere possibile scoprire se la metropolitana di Londra contribuisce a quanto velocemente e quanto fortemente una malattia si diffonde in diverse aree della città, aree che altrimenti sarebbero altrimenti raggiunte dalla malattia più lentamente o con un’incidenza più bassa di casi.
L’ipotesi di un’associazione tra trasporto pubblico e trasmissione della malattia non è nuova. Un altro studio[36] si è concentrato sulla relazione tra l’uso dei trasporti pubblici e l’acquisizione di infezioni respiratorie acute (ARI). Questo studio è più vicino al nostro lavoro perché utilizza un’analisi più microscopica, sia nel tempo che nello spazio. I dati dell’ARI e del controllo di altre condizioni non respiratorie sono stati raccolti dai Medici di Medicina Generale, insieme ai dati sull’utilizzo di autobus o tram nei cinque giorni precedenti l’insorgenza della malattia (casi) o nei cinque giorni precedenti la consultazione (controlli) e i risultati mostrano un’associazione statisticamente significativa tra l’ARI e l’utilizzo di autobus o tram. Inoltre, altri studi hanno evidenziato l’importanza di studiare i modelli metropolitani e le interazioni sociali. In[37], utilizzando i dati delle smart card di viaggio, gli autori costruiscono una rete di incontri sociali a bordo degli autobus pubblici in una città e richiamano l’attenzione sull’impatto che le regolarità collettive possono avere sui vari processi di diffusione/diffusione. Il nostro lavoro, pur affrontando una domanda simile, si differenzia per l’uso di un nuovo metodo analitico che combina la modellazione pedonale a livello individuale e la modellazione compartimentale. Inoltre i due studi[36, 37] analizzano la trasmissione in un ambiente statico (autobus) mentre noi affrontiamo il problema in un ambiente dinamico di persone che si muovono all’interno di stazioni della metropolitana.
I risultati del nostro studio mostrano l’esistenza di una correlazione tra l’uso del trasporto pubblico e la trasmissione di malattie infettive. In particolare, abbiamo mostrato una correlazione tra l’uso della metropolitana di Londra e la diffusione di malattie simil-influenzali. Il modello è particolarmente in grado di mostrare questa correlazione in ambienti con un alto numero di infezioni, catturando il fatto che le aree che hanno il maggior numero di casi di ILI sono anche aree i cui abitanti passano più tempo nella rete metropolitana cambiando linea più frequentemente e entrando in contatto con più individui. La correlazione, tuttavia, non prova la causalità, quando si guarda ad un’epidemia su larga scala, molti fattori che contribuiscono devono essere presi in considerazione. Il ruolo delle disuguaglianze sociali e dell’età nella trasmissione delle malattie infettive è ben noto e pubblicamente accettato[38- 41]. Abbiamo confrontato la correlazione tra i casi di ILI e i contatti originati dall’uso della clandestinità con i coefficienti di correlazione tra i casi di ILI e alcuni fattori demografici come i bambini e le popolazioni anziane, le densità interne dei distretti, i tassi di occupazione e la popolazione a basso reddito (richiedenti le prestazioni) e i nostri risultati mostrano valori simili. Sebbene questi risultati non siano sufficienti a quantificare il ruolo svolto dall’uso del trasporto pubblico sulla trasmissione delle infezioni su larga scala, sono interessanti sia per i ricercatori che per i responsabili politici.
I limiti di questo lavoro sono associati alla natura dei set di dati coinvolti. Dal punto di vista della modellazione, i dati della Oyster card e i dati di tracciamento dei treni sono stati ottenuti in anni diversi (rispettivamente nel 2009 e nel 2013) e, mentre la rete metropolitana non ha subito grandi trasformazioni in quegli anni, i risultati potrebbero essere ancora influenzati da un livello di incertezza sugli orari. Inoltre, il dataset PHE riporta il numero di casi ILI disaggregati solo per distretto e limitati ad una stagione, limitando fortemente la precisione del modello nella valutazione della correlazione tra infezioni e numero di contatti. Inoltre, la conoscenza di dati specifici relativi all’ILI, come la durata dei periodi di incubazione o il diverso livello di infettività fornito dai diversi agenti patogeni che causano l’ILI, renderebbe i risultati più precisi e specifici per ogni caso. Ulteriori studi dovrebbero concentrarsi, in particolare, sull’acquisizione di dati ILI a livello individuale in diversi contesti, in modo che, combinandoli con studi già esistenti in ambito domestico e scolastico, si possa tracciare una mappa più chiara della trasmissione dell’ILI in un ambiente metropolitano, questo potrebbe aiutare a quantificare il ruolo che i diversi punti caldi giocano nella trasmissione. Studi empirici che combinino l’aero-biologia e la modellazione pedonale sarebbero importanti per migliorare la fedeltà dei modelli e per elaborare strategie di controllo non farmacologiche che affrontino le densità di soglia per ridurre al minimo il numero di infezioni e la ventilazione ottimale in diversi ambienti affollati.
I responsabili politici, in particolare, dovrebbero affrontare il ruolo potenzialmente svolto dai trasporti pubblici e dagli eventi affollati ed evitare di incoraggiare la presenza di tali ambienti durante le epidemie, al fine di mantenere il morale pubblico, come fatto specificamente dalla Strategia di preparazione alla pandemia influenzale del Regno Unito[1].
Conclusioni
In sintesi, abbiamo analizzato l’associazione tra l’uso del trasporto pubblico e la trasmissione di malattie infettive studiando la rete della metropolitana di Londra. Abbiamo utilizzato dati reali sui viaggi per dedurre il livello di densità in ogni stazione in qualsiasi momento della giornata e il numero di contatti tra i passeggeri, e abbiamo confrontato questi risultati con i tassi di malattie simil-influenzali (ILI) nei quartieri di Londra. I risultati mostrano una correlazione tra l’uso della metropolitana e i casi di ILI a Londra, in particolare mostrano che un numero maggiore di casi di ILI si verifica in quei quartieri in cui la popolazione passa più tempo in metropolitana e/o ha un numero maggiore di contatti durante il viaggio. D’altra parte, un numero inferiore di casi ILI si verifica in quei quartieri in cui la popolazione ha un uso limitato della metropolitana e/o ha meno contatti. Questi risultati sono in linea con altri fattori ambientali e demografici, come la popolazione stratificata per età, la densità interna di occupazione e il reddito.
Questi risultati sono informativi sia per gli scienziati che per i responsabili politici. Nella fase di ricerca di base, sono necessari ulteriori studi per quantificare esplicitamente il ruolo del trasporto pubblico nella trasmissione delle malattie infettive e le politiche dovrebbero essere rivalutate per tenere conto di questi risultati.
References
- . Accessed May 2018.Publisher Full Text
- Goscé L, Barton DA, Johansson A. Analytical modelling of the spread of disease in confined and crowded spaces. Sci Rep. 2014; 4:4856. DOI | PubMed
- Helbing D, Buzna L, Johansson A, Werner T. Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions. Transp Sci. 2005; 39(1):1-24. DOI
- Johansson A. Constant-net-time headway as a key mechanism behind pedestrian flow dynamics. Phys Rev E. 2009; 80(2):026120. DOI
- Yu W, Johansson A. Modeling crowd turbulence by many-particle simulations. Phys Rev E. 2007; 76(4):046105. DOI
- Helbing D, Johansson A, Al-Abideen HZ. Dynamics of crowd disasters: An empirical study. Phys Rev E. 2007; 75(4):046109. DOI
- Shi J, Ren A, Chen C. Agent-based evacuation model of large public buildings under fire conditions. Autom Constr. 2009; 18(3):338-47. DOI
- Church RL, Cova TJ. Mapping evacuation risk on transportation networks using a spatial optimization model. Transp Res C Emerg Technol. 2000; 8(1-6):321-36. DOI
- Ebihara M, Ohtsuki A, Iwaki H. A model for simulating human behavior during emergency evacuation based on classificatory reasoning and certainty value handling. Comput Aided Civ Infrastruct Eng. 1992; 7(1):63-71. DOI
- Kermack W, Mckendrick A. A contribution to the mathematical theory of epidemics. Proc Roy Soc. 1927; 115:700-21. DOI
- Brauer F. Math Epidemiol. Springer: Berlin; 2008.
- Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys Rev E. 2001; 63(6):066117. DOI
- Newman ME. Spread of epidemic disease on networks. Phys Rev E. 2002; 66(1):016128. DOI
- Cattuto C, Van den Broeck W, Barrat A, Colizza V, Pinton J-F, Vespignani A. Dynamics of person-to-person interactions from distributed rfid sensor networks. PloS ONE. 2010; 5(7):11596. DOI
- Stehlé J, Voirin N, Barrat A, Cattuto C, Isella L, Pinton J-F, Quaggiotto M, Van den Broeck W, Régis C, Lina B. High-resolution measurements of face-to-face contact patterns in a primary school. PloS ONE. 2011; 6(8):23176. DOI
- Vanhems P, Barrat A, Cattuto C, Pinton J-F, Khanafer N, Régis C, Kim B-a, Comte B, Voirin N. Correction: Estimating potential infection transmission routes in hospital wards using wearable proximity sensors. PloS ONE. 2013; 8(9):10-1371. DOI
- . Accessed May 2018.Publisher Full Text
- Xie X, Li Y. How far respiratory droplets move in indoor environments?. Proc Health Build 2006. 2006; 2:309-14.
- Zhu S, Kato S, Yang J-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build Environ. 2006; 41(12):1691-702. DOI
- Zhao B, Zhang Z, Li X. Numerical study of the transport of droplets or particles generated by respiratory system indoors. Build Environ. 2005; 40(8):1032-9. DOI
- . Accessed May 2018.Publisher Full Text
- . Accessed May 2018.Publisher Full Text
- . Accessed May 2018.Publisher Full Text
- . Accessed May 2018.Publisher Full Text
- . Accessed May 2018.Publisher Full Text
- Mossong J, Hens N, Jit M, Beutels P, Auranen K, Mikolajczyk R, Massari M, Salmaso S, Tomba GS, Wallinga J. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008; 5(3):74. DOI
- Fumanelli L, Ajelli M, Merler S, Ferguson NM, Cauchemez S. Model-based comprehensive analysis of school closure policies for mitigating influenza epidemics and pandemics. PLoS Comput Biol. 2016; 12(1):1004681. DOI
- Cauchemez S, Valleron A-J, Boelle P-Y, Flahault A, Ferguson NM. Estimating the impact of school closure on influenza transmission from sentinel data. Nature. 2008; 452(7188):750. DOI | PubMed
- Cauchemez S, Bhattarai A, Marchbanks TL, Fagan RP, Ostroff S, Ferguson NM, Swerdlow D, Group PHW. Role of social networks in shaping disease transmission during a community outbreak of 2009 h1n1 pandemic influenza. Proc Natl Acad Sci. 2011; 108(7):2825-30. DOI | PubMed
- Neuzil KM, Mellen BG, Wright PF, Mitchel Jr EF, Griffin MR. The effect of influenza on hospitalizations, outpatient visits, and courses of antibiotics in children. New Eng J Med. 2000; 342(4):225-31. DOI | PubMed
- Glass LM, Glass RJ. Social contact networks for the spread of pandemic influenza in children and teenagers. BMC Public Health. 2008; 8(1):61. DOI | PubMed
- Sypsa V, Hatzakis A. School closure is currently the main strategy to mitigate influenza a (h1n1) v: a modeling study. Eurosurveillance. 2009; 14(24):19240. DOI | PubMed
- Heymann A, Chodick G, Reichman B, Kokia E, Laufer J. Influence of school closure on the incidence of viral respiratory diseases among children and on health care utilization. Pediatr Infect Dis J. 2004; 23(7):675-7. DOI | PubMed
- Mughini-Gras L, Pijnacker R, Enserink R, Heusinkveld M, van der Hoek W, van Pelt W. Influenza-like illness in households with children of preschool age. Pediatr Infect Dis J. 2016; 35(3):242-8. DOI | PubMed
- Adler AJ, Eames KT, Funk S, Edmunds WJ. Incidence and risk factors for influenza-like-illness in the uk: online surveillance using flusurvey. BMC Infect Dis. 2014; 14(1):232. DOI | PubMed
- Troko J, Myles P, Gibson J, Hashim A, Enstone J, Kingdon S, Packham C, Amin S, Hayward A, Van-Tam JN. Is public transport a risk factor for acute respiratory infection?. BMC Infect Dis. 2011; 11(1):16. DOI | PubMed
- Sun L, Axhausen KW, Lee D-H, Huang X. Understanding metropolitan patterns of daily encounters. Proc Natl Acad Sci. 2013; 110(34):13774-9. DOI | PubMed
- Farmer P. Social inequalities and emerging infectious diseases. Emerg Infect Dis. 1996; 2(4):259. DOI | PubMed
- Marmot M. Social determinants of health inequalities. Lancet. 2005; 365(9464):1099-104. DOI | PubMed
- Gilbert L, Walker L. Treading the path of least resistance: Hiv/aids and social inequalities—a south african case study. Soc Sci Med. 2002; 54(7):1093-110. DOI | PubMed
- Holtgrave DR, Crosby RA. Social capital, poverty, and income inequality as predictors of gonorrhoea, syphilis, chlamydia and aids case rates in the united states. Sex Transm Infect. 2003; 79(1):62-64. DOI | PubMed
Fonte
Goscé L, Johansson A (2018) Analysing the link between public transport use and airborne transmission: mobility and contagion in the London underground. Environmental Health 1784. https://doi.org/10.1186/s12940-018-0427-5





