Calibrazione: il tallone d’Achille dell’analisi predittiva

Background

L’analisi predittiva medica ha guadagnato popolarità negli ultimi anni, con numerose pubblicazioni che si concentrano su modelli che stimano il rischio di una malattia o di uno stato di salute futuro dei pazienti (l'”evento”) basato su algoritmi di regressione classici o su moderni algoritmi flessibili di machine learning o di intelligenza artificiale [1- 3]. Queste previsioni possono supportare il processo decisionale clinico e informare meglio i pazienti. Gli algoritmi (o modelli di previsione del rischio) dovrebbero fornire stime di rischio più elevate per i pazienti con l’evento rispetto ai pazienti senza l’evento (“discriminazione”). Tipicamente, la discriminazione viene quantificata utilizzando l’area sotto la curva caratteristica operativa del ricevitore (AUROC o AUC), nota anche come statistica di concordanza o c-statistica. Inoltre, può essere auspicabile presentare le prestazioni di classificazione a una o più soglie di rischio, come la sensibilità, la specificità e i rapporti di probabilità (specifici dello strato). Qui ci concentriamo sulla calibrazione, un altro aspetto chiave delle prestazioni che viene spesso trascurato. Definiamo la calibrazione, descriviamo il motivo per cui è importante, indichiamo le cause della cattiva calibrazione e riassumiamo come la calibrazione può essere valutata.

Testo principale

La discriminazione è importante, ma le stime dei rischi sono affidabili?

Spesso si dimentica che i rischi stimati possono essere inaffidabili anche quando gli algoritmi hanno una buona discriminazione. Ad esempio, le stime dei rischi possono essere sistematicamente troppo elevate per tutti i pazienti, indipendentemente dal fatto che abbiano sperimentato l’evento o meno. L’accuratezza delle stime di rischio, relativa all’accordo tra il numero stimato e quello osservato di eventi, è chiamata “calibrazione” [4]. Le revisioni sistematiche hanno rilevato che la taratura viene valutata molto meno spesso della discriminazione[2, 3, 5- 7], il che è problematico in quanto una cattiva taratura può rendere le previsioni fuorvianti [8]. Il lavoro precedente ha evidenziato che l’uso di diversi tipi di algoritmi, che variano dalla regressione ad approcci flessibili di machine learning, può portare a modelli che soffrono molto a causa di una cattiva taratura[9, 10]. La calibrazione è stata quindi etichettata come il “tallone d’Achille” dell’analisi predittiva [11]. Il reporting sulle prestazioni di calibrazione è raccomandato dalle linee guida TRIPOD (Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis) per gli studi di modellazione predittiva[12]. La calibrazione è particolarmente importante quando l’obiettivo è quello di sostenere il processo decisionale, anche quando la discriminazione è moderata come per i modelli di previsione del cancro al seno[13]. In questo articolo spieghiamo la rilevanza della calibrazione e suggeriamo soluzioni per prevenire o correggere una calibrazione inadeguata e quindi rendere gli algoritmi predittivi più rilevanti dal punto di vista clinico.

Come possono essere fuorvianti previsioni di rischio inaccurate?

Se l’algoritmo viene utilizzato per informare i pazienti, stime di rischio mal calibrate portano a false aspettative con i pazienti e gli operatori sanitari. I pazienti possono prendere decisioni personali in previsione di un evento, o della sua assenza, che in realtà sono state fuorvianti. Prendiamo, ad esempio, un modello di previsione che prevede la possibilità che il trattamento di fecondazione in vitro (FIVET) porti ad un parto vivo[14]. Indipendentemente da quanto i modelli possano discriminare tra i trattamenti che terminano con un parto vivo e quelli che non lo fanno, è chiaro che una forte sovrastima o sottovalutazione della possibilità di un parto vivo rende gli algoritmi clinicamente inaccettabili. Per esempio, una forte sopravvalutazione della possibilità di un parto vivo dopo la FIVET darebbe false speranze alle coppie che vivono un’esperienza già stressante ed emotiva. Il trattamento di una coppia che, in realtà, ha una prognosi favorevole espone inutilmente la donna a possibili effetti collaterali dannosi, come la sindrome da iperstimolazione ovarica.

Infatti, una cattiva calibrazione può rendere un algoritmo meno utile dal punto di vista clinico di un algoritmo concorrente che ha un AUC inferiore ma è ben calibrato[8]. A titolo di esempio, si consideri il modello QRISK2-2011 e il modello NICE Framingham per prevedere il rischio decennale di malattie cardiovascolari. Uno studio di validazione esterno di questi modelli su 2 milioni di pazienti del Regno Unito ha indicato che QRISK2-2011 era ben calibrato e aveva un AUC di 0,771, mentre NICE Framingham sovrastimava il rischio, con un AUC di 0,776 [15]. Quando si utilizza la tradizionale soglia di rischio del 20% per identificare i pazienti ad alto rischio per l’intervento, QRISK2-2011 selezionerebbe 110 su 1000 uomini di età compresa tra i 35 e i 74 anni. D’altra parte, NICE Framingham ne selezionerebbe quasi il doppio (206 su 1000 uomini) perché un rischio previsto del 20% sulla base di questo modello corrispondeva in realtà a un tasso di eventi più basso. Questo esempio illustra che la sopravvalutazione del rischio porta ad un eccesso di trattamento. Al contrario, la sottovalutazione porta ad un sottotrattamento.

Perché un algoritmo può dare previsioni di rischio mal calibrate?

Molte possibili fonti possono distorcere la calibrazione delle previsioni di rischio. Una prima serie di cause si riferisce a variabili e caratteristiche non correlate allo sviluppo dell’algoritmo. Spesso, le caratteristiche del paziente e i tassi di incidenza o prevalenza della malattia variano notevolmente tra i centri sanitari, le regioni e i paesi[16]. Quando un algoritmo viene sviluppato in un ambiente con un’alta incidenza di malattia, può sistematicamente fornire stime di rischio sovrastimate quando viene utilizzato in un ambiente in cui l’incidenza è più bassa[17]. Per esempio, gli ospedali universitari possono trattare più pazienti con l’evento di interesse rispetto agli ospedali regionali; tale eterogeneità tra i setting può influenzare le stime di rischio e la loro calibrazione[18]. I predittori nell’algoritmo possono spiegare una parte dell’eterogeneità, ma spesso le differenze tra i predittori non spiegano tutte le differenze tra le impostazioni[19]. Anche le popolazioni di pazienti tendono a cambiare nel tempo, ad esempio, a causa di cambiamenti nei modelli di riferimento, nella politica sanitaria o nelle politiche di trattamento[20, 21]. Ad esempio, negli ultimi 10 anni, c’è stata una spinta in Europa per ridurre il numero di embrioni trasferiti in FIV e i miglioramenti nella tecnologia di crioconservazione della FIV hanno portato ad un aumento del congelamento e della conservazione degli embrioni per il successivo trasferimento [22]; tali evoluzioni possono modificare la calibrazione degli algoritmi che prevedono il successo della FIV [23].

Una seconda serie di cause riguarda problemi metodologici relativi all’algoritmo stesso. L’overfitting statistico è comune. È causato da una strategia di modellazione troppo complessa per la quantità di dati a disposizione (ad esempio, troppi predittori candidati, selezione dei predittori basata sulla significatività statistica, uso di un algoritmo molto flessibile come una rete neurale)[24]. Predizioni sovradimensionate catturano troppo rumore casuale nei dati di sviluppo. Così, quando viene convalidato su nuovi dati, ci si aspetta che un algoritmo sovradimensionato mostri prestazioni di discriminazione inferiori e rischi previsti troppo estremi – i pazienti ad alto rischio dell’evento tendono a ottenere previsioni di rischio sovrastimate, mentre i pazienti a basso rischio dell’evento tendono a ottenere previsioni di rischio sottovalutate. A parte l’overfitting statistico, i dati medici di solito contengono errori di misurazione, ad esempio, le espressioni dei biomarcatori variano con i kit di analisi e la misurazione a ultrasuoni della vascolarizzazione tumorale ha una variabilità inter- e intra-osservatore[25, 26]. Se l’errore di misurazione differisce sistematicamente tra le impostazioni (ad esempio, le misurazioni di un predittore sono sistematicamente più polarizzate verso l’alto in un’impostazione diversa), ciò influisce sui rischi previsti e quindi sulla calibrazione di un algoritmo[27].

Come valutare la taratura?

I concetti spiegati in questa sezione sono illustrati nel file aggiuntivo 1, conla validazione dell’algoritmo di rischio di malignità ovarica (ROMA) per la diagnosi di malignità ovarica in donne con un tumore ovarico selezionato per la rimozione chirurgica [28];ulteriori dettagli possono essere trovati altrove [1, 4, 29].

Secondo quattro livelli di calibrazione sempre più rigorosi, i modelli possono essere calibrati in senso medio, debole, moderato o forte[4]. In primo luogo, per valutare la “calibrazione media” (o “calibrazione in grande”), il rischio medio previsto viene confrontato con il tasso di evento complessivo. Quando il rischio medio previsto è superiore al tasso di evento complessivo, l’algoritmo sovrastima il rischio in generale. Al contrario, la sottostima si verifica quando il tasso di evento osservato è superiore al rischio medio previsto.

In secondo luogo, “calibrazione debole” significa che, in media, il modello non sovrastima o sottostima il rischio e non fornisce stime di rischio eccessivamente estreme (troppo vicine a 0 e 1) o modeste (troppo vicine alla prevalenza o all’incidenza della malattia). Una calibrazione debole può essere valutata attraverso l’intercettazione della calibrazione e la pendenza di calibrazione. La pendenza di calibrazione valuta la diffusione dei rischi stimati e ha un valore target di 1. Una pendenza “1” suggerisce che i rischi stimati sono troppo estremi, cioè troppo alti per i pazienti ad alto rischio e troppo bassi per i pazienti a basso rischio. Una pendenza>>1 suggerisce il contrario, cioè che le stime di rischio sono troppo moderate. L’intercettazione della calibrazione, che è una valutazione della calibrazione in grande, ha un valore target di 0; valori negativi suggeriscono una sovrastima, mentre valori positivi suggeriscono una sottostima.

In terzo luogo, una calibrazione moderata implica che i rischi stimati corrispondono alle proporzioni osservate, ad esempio, tra i pazienti con un rischio stimato del 10%, 10 su 100 hanno o sviluppano l’evento. Questo viene valutato con una curva di calibrazione flessibile per mostrare la relazione tra il rischio stimato (sull’asse delle x) e la proporzione osservata degli eventi (asse delle y), ad esempio, utilizzando le funzioni loess o spline. Una curva vicina alla diagonale indica che i rischi previsti corrispondono bene alle proporzioni osservate. In Fig. 1a,b mostriamo alcune curve teoriche, ognuna delle quali corrisponde a diverse intercettazioni di calibrazione e pendenze. Si noti che un’intercetta di taratura vicina a 0 e una pendenza di taratura vicina a 1 non garantiscono che la curva di taratura flessibile sia vicina alla diagonale (vedere il file aggiuntivo 1 per un esempio). Per ottenere una curva di calibrazione precisa, è necessaria una dimensione del campione sufficientemente grande; è stato suggerito un minimo di 200 pazienti con e 200 pazienti senza l’evento[4], sebbene siano necessarie ulteriori ricerche per indagare come fattori come la prevalenza o l’incidenza della malattia influenzino la dimensione del campione richiesta[12]. In piccoli insiemi di dati, è difendibile valutare solo una calibrazione debole calcolando l’intercettazione della calibrazione e la pendenza.Fig. 1Illustrazioni di diversi tipi di errata calibrazione. Le illustrazioni si basano su un risultato con un tasso di evento del 25% ed un modello con un’area sotto la curva ROC (AUC o c-statistica) di 0,71. L’intercettazione della calibrazione e la pendenza sono indicate per ogni curva illustrativa. a Sovravvalutazione o sottovalutazione generale dei rischi previsti. b Rischi previsti troppo estremi o non abbastanza estremi

Quarto, forte calibrazione significa che il rischio previsto corrisponde alla proporzione osservata per ogni possibile combinazione di valori predittivi; ciò implica che la calibrazione è perfetta ed è un obiettivo utopico[4].

Il test comunemente usato da Hosmer-Lemeshow è spesso presentato come un test di calibrazione, anche se ha molti svantaggi – si basa sul raggruppamento artificiale dei pazienti in strati di rischio, dà un valore P che è disinformativo rispetto al tipo e all’entità dell’errore di calibrazione, e soffre di bassa potenza statistica [1, 4]. Pertanto, si consiglia di non utilizzare il test di Hosmer-Lemeshow per valutare la calibrazione.

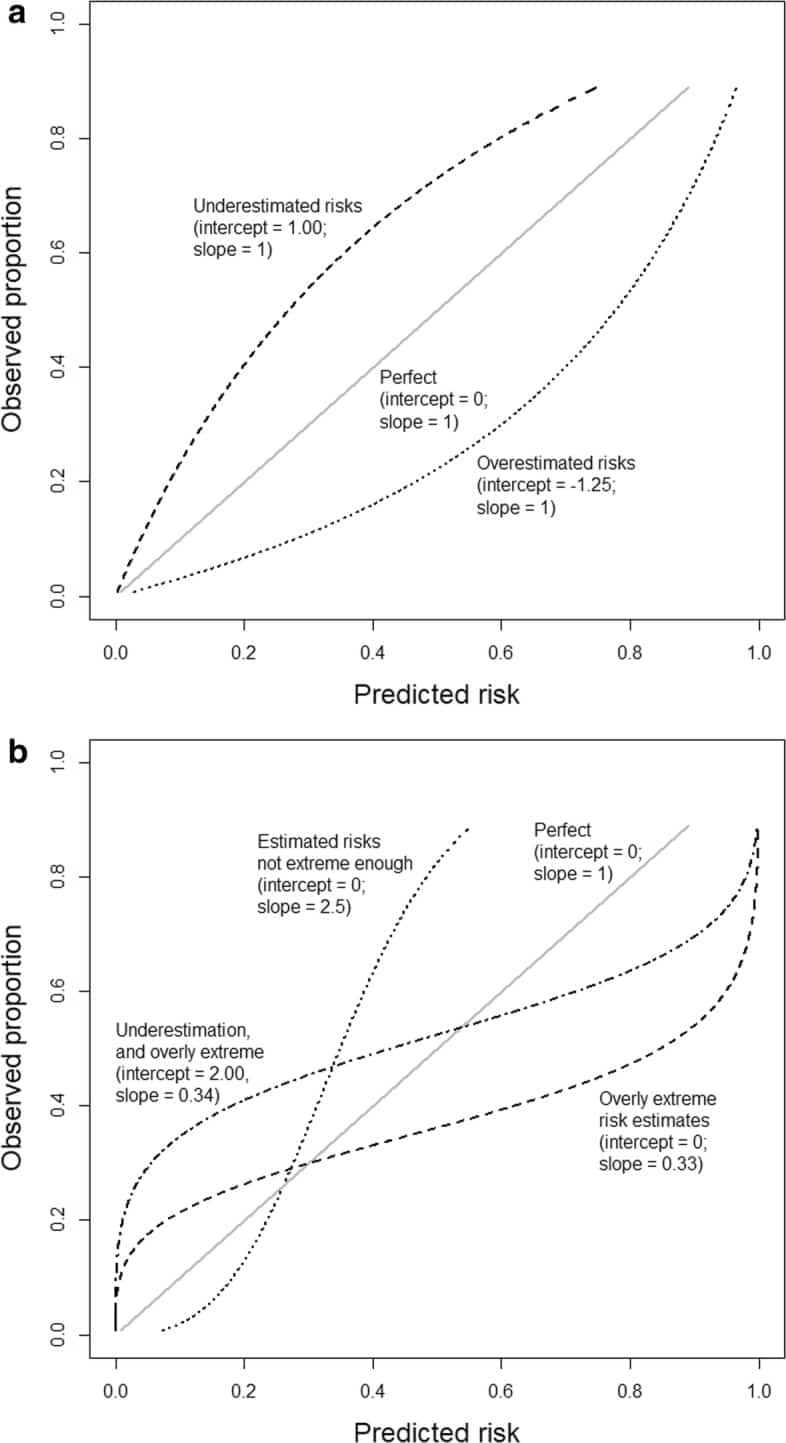
Fig. 1.Illustrazioni di diversi tipi di errore di taratura. Le illustrazioni si basano su un risultato con un tasso di evento del 25% ed un modello con un’area sotto la curva ROC (AUC o c-statistica) di 0,71. L’intercettazione della calibrazione e la pendenza sono indicate per ogni curva illustrativa. a Sovravvalutazione o sottovalutazione generale dei rischi previsti. b Rischi previsti troppo estremi o non abbastanza estremi

Come prevenire o correggere una cattiva taratura?

Quando si sviluppa un algoritmo predittivo, il primo passo consiste nel controllo dell’overfitting statistico. È importante predefinire la strategia di modellazione e garantire che la dimensione del campione sia sufficiente per il numero di predittori considerati[30, 31]. In set di dati più piccoli, dovrebbero essere considerate procedure che mirano a prevenire l’overfitting, ad esempio, utilizzando tecniche di regressione penalizzate come la regressione di Ridge o la regressione del lazo[32] o utilizzando modelli più semplici. I modelli più semplici possono fare riferimento a un minor numero di predittori, omettendo i termini non lineari o di interazione, o utilizzando un algoritmo meno flessibile (ad esempio, regressione logistica invece di foreste casuali o limitando a priori il numero di neuroni nascosti in una rete neurale). Tuttavia, l’uso di modelli troppo semplici può provocare un ritorno di fiamma (file aggiuntivo 1), e la penalizzazione non offre una soluzione miracolosa per l’incertezza in piccoli insiemi di dati [33]. Pertanto, in piccoli dataset di dati, è ragionevole che un modello non venga sviluppato affatto. Inoltre, le procedure di validazione interne possono quantificare la pendenza di calibrazione. In caso di validazione interna, la taratura in grande è irrilevante, poiché la media dei rischi previsti corrisponderà alla velocità dell’evento. Al contrario, la taratura-in-the-large è altamente rilevante nella validazione esterna, dove spesso si nota un disallineamento tra i rischi previsti e quelli osservati.

Quando troviamo previsioni scarsamente calibrate alla validazione, l’aggiornamento dell’algoritmo dovrebbe essere considerato per fornire previsioni più accurate per i nuovi pazienti dall’impostazione di validazione[1, 20]. L’aggiornamento degli algoritmi basati sulla regressione può iniziare con la modifica dell’intercettazione per correggere la calibrazione in grande[34]. Il riadattamento completo dell’algoritmo, come nel caso studio di caso qui sotto, migliorerà la calibrazione se il campione di validazione è relativamente grande[35]. Presentiamo un’illustrazione dettagliata dell’aggiornamento del modello ROMA nel file aggiuntivo 1. Anche le strategie di aggiornamento continuo stanno guadagnando popolarità; tali strategie affrontano dinamicamente i cambiamenti nella popolazione target nel tempo [36].

Pubblicato un caso di studio sulla diagnosi di malattia coronarica ostruttiva

Considerare un modello di regressione logistica per prevedere la malattia coronarica ostruttiva (oCAD) in pazienti con dolore toracico stabile e senza una storia medica di oCAD[37]. Il modello è stato sviluppato su dati di 5677 pazienti reclutati in 18 centri europei e americani, di cui il 31% aveva l’oCAD. L’algoritmo è stato validato esternamente su dati di 4888 pazienti di Innsbruck, Austria, di cui il 44% aveva l’oCAD[38]. L’algoritmo aveva un AUC di 0,69. La calibrazione ha suggerito una combinazione di previsioni di rischio sovrastimate (intercetta – 1.04) ed eccessivamente estreme (pendenza 0.63) (Fig. 2a). La calibrazione è stata migliorata riadattando il modello, cioè rivalutando i coefficienti del predittore (Fig. 2b).Fig. 2Curve di calibrazione durante la validazione di un modello per la malattia coronarica ostruttiva prima e dopo l’aggiornamento. a Curva di calibrazione prima dell’aggiornamento. b Curva di calibrazione dopo l’aggiornamento, rivalutando i coefficienti del modello. La curva flessibile con intervalli di confidenza puntuali (area grigia) si basava sulla regressione locale (loess). Nella parte inferiore dei grafici, gli istogrammi dei rischi previsti sono mostrati per i pazienti con (1) e per i pazienti senza (0) malattia coronarica. Figura adattata da Edlinger et al.[38], che è stato pubblicato sotto la licenza Creative Commons Attribution-Noncommercial (CC BY-NC 4.0)

Fig. 2.Curve di calibrazione durante la validazione di un modello per la malattia coronarica ostruttiva prima e dopo l’aggiornamento. a Curva di calibrazione prima dell’aggiornamento. b Curva di calibrazione dopo l’aggiornamento mediante una nuova stima dei coefficienti del modello. La curva flessibile con intervalli di confidenza puntuali (area grigia) si basava sulla regressione locale (loess). Nella parte inferiore dei grafici, gli istogrammi dei rischi previsti sono mostrati per i pazienti con (1) e per i pazienti senza (0) malattia coronarica. Figura adattata da Edlinger et al.[38], che è stato pubblicato sotto la licenza Creative Commons Attribution-Noncommercial (CC BY-NC 4.0)

Conclusioni

Gli argomenti chiave di questo documento sono riassunti nella Tabella 1. Algoritmi predittivi mal calibrati possono essere fuorvianti, il che può portare a decisioni cliniche errate e potenzialmente dannose. Pertanto, abbiamo bisogno di strategie di modellazione prespecificate che siano ragionevoli rispetto alla dimensione del campione disponibile. Quando si convalidano gli algoritmi è imperativo valutare la calibrazione usando misure e visualizzazioni appropriate – questo ci aiuta a capire come l’algoritmo si comporta in una particolare impostazione, dove le previsioni possono andare male, e se l’algoritmo può trarre beneficio dall’aggiornamento. A causa dei sistemi sanitari locali e dei modelli di riferimento, sono previste differenze di popolazione tra i centri e le regioni; è probabile che i modelli di previsione non includano tutti i predittori necessari ad accogliere queste differenze. Insieme al fenomeno delle derive di popolazione, i modelli richiedono idealmente un monitoraggio continuo in contesti locali per massimizzare i benefici nel tempo. Questo argomento diventerà ancora più vitale con la crescente popolarità di algoritmi altamente flessibili. L’obiettivo finale è quello di ottimizzare l’utilità dell’analisi predittiva per il processo decisionale condiviso e la consulenza al paziente.
Tabella 1Punti principali sulla calibraturaPerché la calibratura è importante- Le decisioni sono spesso basate sul rischio, quindi i rischi previsti dovrebbero essere affidabili- Una cattiva calibratura può rendere un modello di previsione clinicamente inutile o addirittura dannosoCausa di una cattiva calibratura- Sovrapposizione statistica ed errore di misura- Eterogeneità nelle popolazioni in termini di caratteristiche del paziente, incidenza o prevalenza della malattia, gestione del paziente e politiche di trattamentoLa valutazione della calibratura nella pratica- La perfetta calibratura, dove i rischi previsti sono corretti per ogni modello covariato, è utopica; non dovremmo puntare a questo- Nello sviluppo del modello, concentrarci sugli effetti non lineari e sui termini di interazione solo se è disponibile un campione di dimensioni sufficientemente grandi; dimensioni ridotte del campione richiedono strategie di modellazione più semplici o che non venga sviluppato alcun modello- Evitare l’Hosmer-Lemeshow test per valutare o provare la calibratura- Alla validazione interna, concentrarsi sulla pendenza di calibrazione come parte della valutazione dell’overfitting statistico- Alla validazione esterna, concentrarsi sulla curva di calibrazione, l’intercettazione e la pendenza- L’aggiornamento del modello dovrebbe essere considerato in caso di scarsa calibrazione; la rivalutazione del modello richiede interamente dati sufficienti

Informazioni supplementari

File aggiuntivo 1. Illustrazione dettagliata della valutazione della calibrazione e dell’aggiornamento del modello: il modello di regressione logistica ROMA.

References

1. Steyerberg EW. Clinical prediction models. Springer: New York; 2009.
2. Wessler BS, Paulus J, Lundquist CM. Tufts PACE clinical predictive model registry: update 1990 through 2015. Diagn Progn Res. 2017; 1:10. DOI | PubMed
3. Kleinrouweler CE, Cheong-See FM, Collins GS. Prognostic models in obstetrics: available, but far from applicable. Am J Obstet Gynecol. 2016; 214:79-90. DOI | PubMed
4. Van Calster B, Nieboer D, Vergouwe Y, De Cock B, Pencina MJ, Steyerberg EW. A calibration hierarchy for risk models was defined: from utopia to empirical data. J Clin Epidemiol. 2016; 74:167-176. DOI | PubMed
5. Collins GS, de Groot JA, Dutton S. External validation of multivariable prediction models: a systematic review of methodological conduct and reporting. BMC Med Res Methodol. 2014; 14:40. DOI | PubMed
6. Christodoulou E, Ma J, Collins GS, Steyerberg EW, Verbakel JY, Van Calster B. A systematic review shows no performance benefit of machine learning over logistic regression for clinical prediction models. J Clin Epidemiol. 2019; 110:12-22. DOI | PubMed
7. Bouwmeester W, Zuithoff NPA, Mallett S. Reporting and methods in clinical prediction research: a systematic review. PLoS Med. 2012; 9:1-12. DOI
8. Van Calster B, Vickers AJ. Calibration of risk prediction models: impact on decision-analytic performance. Med Decis Mak. 2015; 35:162-169. DOI
9. Van Hoorde K, Van Huffel S, Timmerman D, Bourne T, Van Calster B. A spline-based tool to assess and visualize the calibration of multiclass risk predictions. J Biomed Inform. 2015; 54:283-293. DOI | PubMed
10. Van der Ploeg T, Nieboer D, Steyerberg EW. Modern modeling techniques had limited external validity in predicting mortality from traumatic brain injury. J Clin Epidemiol. 2016; 78:83-89. DOI | PubMed
11. Shah ND, Steyerberg EW, Kent DM. Big data and predictive analytics: recalibrating expectations. JAMA.. 2018; 320:27-28. DOI | PubMed
12. Moons KG, Altman DG, Reitsma JB. Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med. 2015; 162:W1-W73. DOI | PubMed
13. Yala A, Lehman C, Schuster T, Portnoi T, Barzilay R. A deep learning mammography-based model for improved breast cancer risk prediction. Radiology.. 2019; 292:60-66. DOI | PubMed
14. Dhillon RK, McLernon DJ, Smith PP. Predicting the chance of live birth for women undergoing IVF: a novel pretreatment counselling tool. Hum Reprod. 2016; 31:84-92. DOI | PubMed
15. Collins GS, Altman DG. Predicting the 10 year risk of cardiovascular disease in the United Kingdom: independent and external validation of an updated version of QRISK2. BMJ.. 2012; 344:e4181. DOI | PubMed
16. Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin. 2018; 68:394-424. DOI | PubMed
17. Testa A, Kaijser J, Wynants L. Strategies to diagnose ovarian cancer: new evidence from phase 3 of the multicentre international IOTA study. Br J Cancer. 2014; 111:680-688. DOI | PubMed
18. Riley RD, Ensor J, Snell KI. External validation of clinical prediction models using big datasets from e-health records or IPD meta-analysis: opportunities and challenges. BMJ.. 2016; 353:i3140. DOI | PubMed
19. Steyerberg EW, Roobol MJ, Kattan MW, van der Kwast TH, de Koning HJ, Schröder FH. Prediction of indolent prostate cancer: validation and updating of a prognostic nomogram. J Urol. 2007; 177:107-112. DOI | PubMed
20. Davis SE, Lasko TA, Chen G, Siew ED, Matheny ME. Calibration drift in regression and machine learning models for acute kidney injury. J Am Med Inform Assoc. 2017; 24:1052-1061. DOI | PubMed
21. Thai TN, Ebell MH. Prospective validation of the good outcome following attempted resuscitation (GO-FAR) score for in-hospital cardiac arrest prognosis. Resuscitation.. 2019; 140:2-8. DOI | PubMed
22. Leijdekkers JA, Eijkemans MJC, van Tilborg TC. Predicting the cumulative chance of live birth over multiple complete cycles of in vitro fertilization: an external validation study. Hum Reprod. 2018; 33:1684-1695. DOI | PubMed
23. te Velde ER, Nieboer D, Lintsen AM. Comparison of two models predicting IVF success; the effect of time trends on model performance. Hum Reprod. 2014; 29:57-64. DOI | PubMed
24. Steyerberg EW, Uno H, Ioannidis JPA, Van Calster B. Poor performance of clinical prediction models: the harm of commonly applied methods. J Clin Epidemiol. 2018; 98:133-143. DOI | PubMed
25. Murthy V, Rishi A, Gupta S. Clinical impact of prostate specific antigen (PSA) inter-assay variability on management of prostate cancer. Clin Biochem. 2016; 49:79-84. DOI | PubMed
26. Wynants L, Timmerman D, Bourne T, Van Huffel S, Van Calster B. Screening for data clustering in multicenter studies: the residual intraclass correlation. BMC Med Res Methodol. 2013; 13:128. DOI | PubMed
27. Luijken K, Groenwold RHH, Van Calster B, Steyerberg EW, van Smeden M. Impact of predictor measurement heterogeneity across settings on performance of prediction models: a measurement error perspective. Stat Med. 2019; 38:3444-3459. PubMed
28. Moore RG, McMeekin DS, Brown AK. A novel multiple marker bioassay utilizing HE4 and CA125 for the prediction of ovarian cancer in patients with a pelvic mass. Gynecol Oncol. 2009; 112:40-46. DOI | PubMed
29. Austin PC, Steyerberg EW. Graphical assessment of internal and external calibration of logistic regression models by using loess smoothers. Stat Med. 2014; 33:517-535. DOI | PubMed
30. van Smeden M, Moons KGM, de Groot JA. Sample size for binary logistic prediction models: beyond events per variable criteria. Stat Meth Med Res.. 2019; 28:2455-2474. DOI
31. Riley RD, Snell KIE, Ensor J. Minimum sample size for developing a multivariable prediction model: PART II – binary and time-to-event outcomes. Stat Med. 2019; 38:1276-1296. DOI | PubMed
32. Moons KGM, Donders AR, Steyerberg EW, Harrell FE. Penalized maximum likelihood estimation to directly adjust diagnostic and prognostic prediction models for overoptimism: a clinical example. J Clin Epidemiol. 2004; 57:1262-1270. DOI | PubMed
33. . Accessed 10 Oct 2019.Publisher Full Text
34. Steyerberg EW, Borsboom GJJM, van Houwelingen HC, Eijkemans MJC, Habbema JDF. Validation and updating of predictive logistic regression models: a study on sample size and shrinkage. Stat Med. 2004; 23:2567-2586. DOI | PubMed
35. Su TL, Jaki T, Hickey GL, Buchan I, Sperrin M. A review of statistical updating methods for clinical prediction models. Stat Meth Med Res. 2018; 27:185-197. DOI
36. Hickey GL, Grant SW, Caiado C. Dynamic prediction modeling approaches for cardiac surgery. Circ Cardiovasc Qual Outcomes. 2013; 6:649-658. DOI | PubMed
37. Genders TSS, Steyerberg EW, Hunink MG. Prediction model to estimate presence of coronary artery disease: retrospective pooled analysis of existing cohorts. BMJ.. 2012; 344:e3485. DOI | PubMed
38. Edlinger M, Wanitschek M, Dörler J, Ulmer H, Alber HF, Steyerberg EW. External validation and extension of a diagnostic model for obstructive coronary artery disease: a cross-sectional predictive evaluation in 4888 patients of the Austrian Coronary Artery disease Risk Determination In Innsbruck by diaGnostic ANgiography (CARDIIGAN) cohort. BMJ Open. 2017; 7:e014467. DOI