Abstract
Introduzione
La neuroimmagine e soprattutto la risonanza magnetica funzionale (fMRI) ha fatto molta strada dai primi esperimenti all’inizio degli anni ’90. Questi impressionanti risultati sono curiosi alla luce dei limiti della fMRI. La risposta sangue-ossigeno dipendente dal livello di ossigeno (BOLD) misurata dalla fMRI è una misura rumorosa e indiretta dell’attività neurale (Logothetis,2002, 2008; O‘Herron et al.,2016) da cui i ricercatori cercano di dedurre la funzione neurale.
La risposta di BOLD scia l’attività neurale di 2 s, raggiunge picchi da 5 a 6 s, e ritorna alla linea di base intorno a 10 s, mentre l’attività neurale si verifica sull’ordine dei millisecondi e può essere breve(Huettel et al., In termini di risoluzione spaziale, la risposta di BOLD può allontanarsi di oltre millimetri dall’attività neurale a causa dei contributi dei segnali venosi (Turner,2002). Allo stesso modo, le differenze nella risposta di BOLD possono derivare da differenze accidentali nelle proprietà vascolari delle regioni cerebrali (Ances et al.,2009). Tali fonti di rumore possono potenzialmente implicare differenze nell’attività neurale in regioni dove non ci dovrebbero essere.
Lo stesso processo di acquisizione dei dati pone dei limiti alla misurazione della fMRI. Gli artefatti del movimento (ad esempio, i movimenti della testa da parte di soggetti umani) e la non uniformità del campo magnetico riducono la qualità dei dati. Nelle analisi, le immagini tridimensionali sono costruite a partire da fette acquisite in tempi leggermente diversi. Una volta raccolti, i dati fMRI sono tipicamente levigati durante le analisi (Carp,2012). Tutti questi fattori pongono limiti a ciò che fMRI può misurare.
Nonostante queste debolezze, la fMRI si è rivelata uno strumento incredibilmente utile. Ad esempio, ora sappiamo che i processi cognitivi di base coinvolti nel linguaggio (Binderet al., 1997) e nella memoria di lavoro (Pessoaet al., 2002) sono distribuiti in tutta la corteccia. Questi risultati hanno messo in discussione la nozione che le facoltà cognitive sono in una corrispondenza uno a uno con le regioni cerebrali.
I progressi nell’analisi dei dati hanno aumentato ciò che può essere dedotto dalla fMRI(De Martino et al., 2008). Uno di questi progressi è l’analisi multivariata dei modelli (MVPA), che decodifica un modello di attività neurale al fine di valutare le informazioni contenute all’interno (Coxe Savoia, 2003). Piuttosto che calcolare i contrasti statistici univariati, come il confronto dell’attività complessiva di BOLD per una regione quando viene mostrato un volto o uno stimolo della casa, MVPA prende in considerazione i modelli voxel.
Utilizzando l’MVPA, si può effettuare la cosiddetta ‘lettura della mente’ – specifici stati cerebrali possono essere decodificati data l’attività fMRI (Norman et al., 2006), rivelando la rappresentazione corticale e l’organizzazione in dettaglio impressionante. Ad esempio, utilizzando queste tecniche di analisi in coppia con fMRI possiamo sapere se un partecipante è ingannevole in un gioco (Davatzikos et al.,2005), e possiamo determinare se un partecipante sta leggendo una frase ambigua e dedurre la categoria semantica di una parola che sta leggendo(Mitchell et al., 2004).
L’analisi della somiglianza rappresentazionale (RSA), un’altra tecnica multivariata, è particolarmente adatta per esaminare la struttura rappresentazionale(Kriegeskorte et al., 2008; Kriegeskorte, 2009). Ci concentreremo sulla RSA più avanti in questo contributo, quindi considereremo questa tecnica in qualche dettaglio. La RSA confronta direttamente la somiglianza (ad es, Ad esempio, l’attività neurale derivante dalla visione di un pettirosso e di un passero può essere più simile tra loro che tra un pettirosso e un pinguino.
Queste somiglianze neurali a coppie possono essere confrontate con quelle previste da un particolare modello teorico per determinare le corrispondenze. Ad esempio, Mack et al. (2013) hanno identificato regioni cerebrali in cui la struttura di somiglianza neurale corrispondeva a quella di un modello cognitivo di categorizzazione umana, che è stato utile per dedurre la funzione di varie regioni cerebrali. Le somiglianze neurali stesse possono essere visualizzate applicando la scala multidimensionale per comprendere ulteriormente le proprietà dello spazio (Daviset al., RSA è stato utile in una serie di altri sforzi, come la comprensione del ruolo di varie aree cerebrali nel ripristinare le esperienze passate (Tomparyet al., 2016; Mack e Preston, 2016).
Dati i limiti della fMRI nella misurazione dell’attività neurale, ci si potrebbe chiedere come sia possibile che metodi come la RSA abbiano successo. La risposta di BOLD è temporalmente e spazialmente imprecisa, eppure sembra che i ricercatori possano dedurre proprietà generali delle rappresentazioni neurali che si collegano in modo sensato allo stimolo e al comportamento.Il codice neurale deve avere determinate proprietà perché questo stato di cose possa avere successo. Quali tipi di modelli o calcoli sono coerenti con il successo della fMRI? Se il cervello è un dispositivo di calcolo, dovrebbe essere di un tipo particolare perché la fMRI sia utile, dati i suoi limiti nella misurazione dell’attività neurale.
La fluidità e il codice neurale
Affinché la fMRI possa recuperare gli spazi di somiglianza neurale, il codice neurale deve mostrare determinate proprietà. In primo luogo, il codice neurale non può essere così a grana così fine che i limiti di risoluzione temporale e spaziale della fMRI rendono impossibile risolvere le differenze di rappresentazione. In secondo luogo, deve essere parzialmente soddisfatta anche una nozione di fluidità funzionale, che introdurremo e definiremo.
La disomogeneità di Voxel nello spazio e nel tempo
La risposta di BOLD riassume l’attività neurale nello spazio e nel tempo, il che pone dei limiti a ciò che la fMRI può misurare. Per fare un’analogia, 3+5 e 6+2 sono entrambi pari a 8 attraverso percorsi diversi. Se i diversi ‘percorsi’ dell’attività neurale sono consequenziali al codice neurale e sono sommati nella risposta in BOLD, allora la fMRI sarà cieca alle differenze di rappresentazione.
Per catturare le differenze di rappresentazione, la risposta voxel deve essere disomogenea sia tra i voxel che all’interno di un voxel nel tempo. Si considerino gli analoghi fMRI mostrati in Figura 1; parallelizzando i neuroni con i pixel e i voxel con i quadrati sulla griglia sovrapposta. L’immagine in alto a sinistra rappresenta l’attività neurale che varia in modo uniforme in modo tale che le transizioni dal rosso al giallo avvengano in incrementi progressivi. Riassumendo all’interno di un quadrato, cioè di un voxel, non si altererà drasticamente la vista ad alto livello di una transizione graduale dal rosso al giallo (immagine in basso a sinistra). La risposta del voxel è disomogenea, il che permetterebbe la decodifica tramite fMRI (cfr. Kamitanie Tong,2005; Alink etal., 2013). Alterare la dimensione della griglia (cioè il voxel) non avrà un impatto drammatico sui risultati finché il quadrato non diventerà così grande da sottrarre la maggior parte dei pixel (cioè, Questo risultato è in linea con i concetti di base della teoria dell’informazione, come il teorema di campionamento Nyquist-Shannon. La chiave è che i pixel/neuroni rossi e gialli sono topologicamente organizzati: la loro relazione tra loro è a tutti gli effetti invariata rispetto alla granularità dei quadrati/voxel (per maggiori dettagli vedere: Chaimow et al., 2011; Freeman et al., 2011; Swisher et al., 2010).10.7554/eLife.21397.003Figure 1.L’attività dei neuroni nel pannello in alto a sinistra cambia gradualmente da sinistra a destra, mentre i cambiamenti sono più bruschi nei pannelli in alto a destra e in alto a destra. Per il modello più fluido dell’attività neurale, la sommatoria di ogni voxel (in basso a sinistra) cattura il gradiente di cambiamento da sinistra a destra raffigurato in alto a sinistra, mentre per la rappresentazione meno liscia nel pannello centrale tutti i voxel sommano allo stesso valore arancione (in basso al centro). Quindi, le differenze nell’attivazione dei neuroni gialli vs. rossi sono rilevabili usando la fMRI per il caso liscio, ma non per il caso meno liscio perché la risposta dei voxel è omogenea. Il miglioramento della risoluzione spaziale (pannelli di destra) riducendo le dimensioni dei voxel supera questi limiti di campionamento, con conseguente disomogeneità dei voxel (pannello in basso a destra).DOI:http://dx.doi.org/10.7554/eLife.21397.003
Al contrario, l’immagine in alto al centro della figura 1 comporta drammatici cambiamenti di rappresentazione all’interno di voxel. Ogni voxel (quadrato nella griglia), in questo caso, produrrà un colore arancione omogeneo quando il suo contenuto viene sommato. Così, sommando il contenuto di un voxel in questo caso si cancella il contenuto rappresentativo: rosso e giallo; restituendo invece quadrati/voxel che sono tutti dello stesso colore uniforme: arancione. Questo insuccesso è dovuto a limiti di campionamento che potrebbero essere affrontati da voxel più piccoli (vedi colonna più a destra). Purtroppo, i voxel arbitrariamente piccoli con alte frequenze di campionamento non sono un lusso che si può concedere alla fMRI.
Il successo della fMRI, dati i suoi limiti di campionamento, è coerente con gli schemi di codifica neurale proposti, come la codifica della popolazione(Averbeck et al., 2006; Panzeri et al., 2015; Pouget et al., 2000) nei casi in cui i neuroni con sintonie simili si raggruppano spazialmente (ad es, Nella codifica della popolazione , i neuroni contribuiscono congiuntamente a rappresentare uno stimolo in modo molto simile a quanto i pixel contribuivano a rappresentare colori diversi nella colonna più a sinistra della Figura 1. Quando questa disomogeneità si rompe, le strutture di somiglianza dovrebbero essere difficili da recuperare usando la fMRI. Infatti, un recente studio con le scimmie macacche che ha preso in considerazione sia le misure monocellulari che quelle fMRI supporta questo punto di vista – gli aspetti di stimolo che erano scarsamente raggruppati spazialmente in termini di selettività delle singole cellule erano più difficili da decodificare dalla risposta di BOLD (Duboiset al., 2015).
Gli stessi principi si estendono dal dominio spaziale a quello temporale. La risposta di BOLD sarà cieca alle differenze tra le rappresentazioni nella misura in cui il cervello si basa sulla precisa tempistica dell’attività neurale per codificare le informazioni. Per esempio, nella codifica di burstiness, le rappresentazioni neurali si distinguono l’una dall’altra non per il loro tasso di scatto medio, ma per la varianza della loro attività(Fano, 1947; Katz, 1996). Secondo questo schema di codifica, i valori di stimolo più intensi sono rappresentati da unità di burstier, non da unità che sparano più in generale. La somiglianza neurale non è recuperabile dalla fMRI in uno schema di codifica di burstiness. Poiché il segnale di BOLD si somma approssimativamente nel tempo (Boyntonet al., 1996), gli eventi di sparo si sommano allo stesso numero indipendentemente dalla loro burstiness.
Allo stesso modo, l’attività di BOLD può essere un insieme di attività sincronizzate a più frequenze. Sebbene il potenziale del campo locale in banda gamma sia maggiormente associato alla risposta di BOLD, anche le oscillazioni in altre bande di frequenza possono contribuire alla risposta di BOLD(Magri et al., 2012; Scheeringaet al., 2011). Se così fosse, l’fMRI non riuscirebbe a distinguere tra gli stati rappresentazionali che si differenziano per l’equilibrio dei contributi tra le bande, proprio come l’esempio aritmetico all’inizio di questa sottosezione in cui diversi addendi danno la stessa somma. Come in precedenza, i concetti di base della teoria dell’informazione, come il teorema di campionamento Nyquist-Shannon, implicano che gli schemi di codifica temporalmente impegnativi saranno invisibili alla fMRI (cfr. Nevado et al., 2004).
Il successo della fMRI non implica che il cervello non utilizzi informazioni temporali precise, ma significa che tali schemi di codifica temporalmente impegnativi non possono essere la storia completa dati i successi della fMRI nel rivelare rappresentazioni neurali. Invece, il codice neurale deve includere nella sua miscela almeno alcuni schemi di codifica che sono coerenti con i successi della fMRI. Ad esempio, la codifica del tasso(Adrian e Zotterman, 1926) in cui la frequenza con cui i neuroni sparano è una funzione dell’intensità di uno stimolo è coerente con il successo della fMRI perché i cambiamenti nel tasso di sparamento per una popolazione di cellule dovrebbero essere recuperabili dalla fMRI come più flussi di sangue alle cellule più attive(O’Herron et al., 2016).
Questi esempi chiariscono che il codice neurale deve essere in qualche modo spazialmente e temporalmente liscio rispetto all’attività neurale (che è diversi ordini di grandezza più piccoli dei voxel) perché la fMRI abbia successo. Qualunque cosa stia accadendo nei circa un milione di neuroni all’interno di un voxel (Huettelet al., 2009) attraverso il tempo viene parzialmente riflessa dalla somma di BOLD, che non sarebbe il caso se ogni neurone stesse calcolando qualcosa di drammaticamente diverso per una discussione approfondita, vedi:(Kriegeskorte et al., 2010).
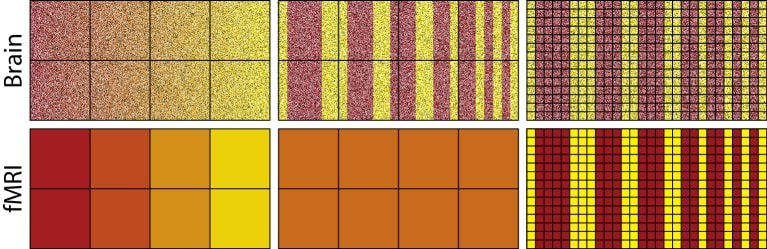
Figura 1.L’attività dei neuroni nel pannello in alto a sinistra cambia gradualmente da sinistra a destra, mentre i cambiamenti sono più bruschi nei pannelli in alto a destra e in alto a destra.Ogni quadrato nella griglia rappresenta un voxel che riassume l’attività all’interno della sua cornice, come mostrato nei pannelli in basso. Per il modello più fluido dell’attività neurale, la sommatoria di ogni voxel (in basso a sinistra) cattura il gradiente di cambiamento da sinistra a destra raffigurato in alto a sinistra, mentre per la rappresentazione meno liscia nel pannello centrale tutti i voxel sommano allo stesso valore arancione (in basso al centro). Quindi, le differenze nell’attivazione dei neuroni gialli vs. rossi sono rilevabili usando la fMRI per il caso liscio, ma non per il caso meno liscio perché la risposta dei voxel è omogenea. Il miglioramento della risoluzione spaziale (pannelli di destra) riducendo le dimensioni dei voxel supera questi limiti di campionamento, con conseguente disomogeneità dei voxel (pannello in basso a destra).DOI:
http://dx.doi.org/10.7554/eLife.21397.003
Fluidità funzionale
Una conclusione generale è che aspetti importanti del codice neurale sono spazialmente e temporalmente lisci. In un certo senso, questa nozione di fluidità è banale in quanto implica semplicemente che i cambiamenti nell’attività neurale devono essere visibili nella risposta di BOLD (cioè, disomogeneità a voce trasversale) perché la fMRI abbia successo. In questa sezione, ci concentriamo su un senso più sottile di fluidità che deve anche essere soddisfatto, cioè la fluidità funzionale.
I voxel vicini contengono prevalentemente rappresentazioni simili (Norman et al., 2006), cioè sono topologicamente organizzati come nella Figura 1. Tuttavia, la scorrevolezza super-voxel non è né necessaria né sufficiente perché la fMRI riesca a recuperare la struttura di somiglianza. Al contrario, deve essere soddisfatta una nozione più generale di fluidità funzionale, in cui gli stimoli simili corrispondono a rappresentazioni interne simili. Sebbene il super-voxel e la scorrevolezza funzionale siano entrambi specificati a livello di super-voxel, questi concetti distinti non devono essere confusi. Una funzione f che mappi da qualche ingresso x all’uscita y è funzionalmente scorrevole se e solo se(1)sim(x1,x2)∝sim(y1,y2),
dove f(x1)=y1 e f(x2)=y2. Ad esempio, x e y potrebbero essere le stime beta per i voxel in due regioni cerebrali e sim potrebbe essere la correlazione di Pearson. Per misurare la scorrevolezza funzionale, il grado di proporzionalità tra tutte le possibili coppie di somiglianza sim(x1,x2) e sim(y1,y2) potrebbe anche essere valutato dalla correlazione di Pearson (cioè, la somiglianza tra una coppia y1 e y2 aumenta all’aumentare della somiglianza tra la coppia corrispondente x1 e x2). Per definizione, la fluidità funzionale deve essere preservata nel codice neurale affinché la fMRI recuperi le corrispondenze di somiglianza (come nella RSA), sia che queste corrispondenze siano tra stimoli (ad esempio, xs) e attività neurale (ad esempio, ys), regioni cerebrali multiple (ad esempio, xs e ys), o misura modello (ad esempio, xs) e qualche regione cerebrale (ad esempio, ys).
Da questa definizione, dovrebbe essere chiaro che la scorrevolezza funzionale è distinta dalla scorrevolezza super-voxel. Ad esempio, un’area cerebrale che mostrasse modelli di attività liscia attraverso voxel per ogni singolo stimolo del viso, ma la cui attività non riflettesse la struttura di somiglianza degli stimoli, sarebbe super-voxel liscia, ma non funzionalmente liscia rispetto allo stimolo impostato. Al contrario, una sezione successiva di questo contributo discute come le reti neurali con pesi casuali sono funzionalmente ma non super-voxel lisce.
Per contribuire ad introdurre il concetto di fluidità funzionale, consideriamo due schemi di codifica utilizzati nelle applicazioni di ingegneria, la codifica fattoriale e la codifica hash, che sono entrambi incoerenti con il successo della fMRI perché non preservano la fluidità funzionale. Nella sezione successiva, consideriamo schemi di codifica, come le reti di apprendimento profondo, che sono funzionalmente lisci in varia misura e sono coerenti con il successo della fMRI.
Codifica del design fattoriale
Il design fattoriale è strettamente legato alla nozione di gerarchia. Ad esempio, gli approcci gerarchici al riconoscimento degli oggetti umani (Serree Poggio, 2010) propongono di combinare elementi visivi semplici (ad esempio, una linea orizzontale o verticale) per formare elementi più complessi (ad esempio, una croce). Da una prospettiva fattoriale, gli elementi semplici possono essere considerati come effetti principali e gli elementi complessi, che riflettono la combinazione di elementi semplici, come interazioni.
Nella Tabella 1, un disegno fattoriale completo a due livelli è mostrato con tre fattori A, B, C, tre interazioni a due vie AB, AC, BC, e un’interazione a tre vie ABC, così come un termine di intercettazione. Tutte le colonne della matrice del disegno sono ortogonali a coppie.10.7554/eLife.21397.004Tabella 1.Matrice del disegno per un disegno fattoriale completo.DOI:http://dx.doi.org/10.7554/eLife.21397.004IABCABACBCABC1-1-1-1111-111-1-1-1-1111-11-1-11-11111-11-1-1-11-1-111-1-1111-11-11-1-11-111-1-11-111111111
Applicare il concetto di disegno fattoriale alla modellazione del codice neurale significa trattare ogni riga della Tabella 1 come una rappresentazione. Per esempio, ogni voce in una riga potrebbe corrispondere al livello di attività di un voxel. È interessante notare che, se una qualsiasi regione del cervello avesse una tale distribuzione di voxel, la somiglianza neurale sarebbe impossibile da recuperare con la fMRI. La ragione di ciò è che ogni rappresentazione (cioè riga nella Tabella 1) è ortogonale ad ogni altra riga, il che significa che la somiglianza neurale è la stessa per qualsiasi coppia di elementi. Quindi, questo schema di codifica non può scoprire che le basse distorsioni sono più simili ad un prototipo di categoria che le alte distorsioni.
Piuttosto che dimostrarlo con una simulazione, possiamo fornire una semplice prova per fare questo caso usando l’algebra lineare di base. Dividendo ogni elemento nella matrice di disegno n×n (cioè, Tabella 1) per n, si rende ogni colonna ortogonale, cioè ogni colonna rappresenterà un vettore unitario e sarà ortogonale alle altre colonne. Questa condizione significa che la matrice di disegno è ortogonale. Per una matrice ortogonale, Q, come la nostra matrice di disegno, vale la seguente proprietà: Q×QT=QT×Q=I; dove QT è la trasposizione di Q (una matrice ottenuta scambiando colonne e righe), e I è la matrice di identità. Questa proprietà delle matrici ortogonali implica che le righe e le colonne della matrice fattoriale di disegno sono intercambiabili, e che sia le righe che le colonne sono ortogonali.
Le rappresentazioni interne create con una matrice fattoriale non si raggruppano in modo da riflettere in modo significativo la struttura categoriale degli input. Dato che ogni rappresentazione è creata in modo tale da essere ortogonale ad ogni altra, non ci può essere modo di far emergere informazioni, correlazioni all’interno e tra le categorie. Due input che variano in una sola dimensione (ad esempio, pixel) avrebbero una somiglianza zero; questo non è intrinsecamente fluido dal punto di vista funzionale. In termini di Equazione 1 e Tabella 1, una x sarebbe un vettore tridimensionale costituito dai valori di A, B e C, mentre la sua y sarebbe l’intera riga corrispondente della tabella. Tralasciando il caso degenerato dell’autosimilarità, non esiste una relazione proporzionale tra le coppie di somiglianza perché tutte le coppie y hanno somiglianza zero. Se il codice neurale di una regione utilizzasse una tecnica simile al disegno fattoriale, gli studi di neuroimaging non scoprirebbero mai le strutture di somiglianza osservando i modelli di attività dei voxel in quella regione.
Hash funzione di codifica
Le funzioni Hash assegnano uscite univoche arbitrarie agli ingressi univoci, il che è potenzialmente utile per qualsiasi sistema di memoria, sia esso digitale o biologico. Tuttavia, un tale schema di codifica non è funzionalmente regolare dal punto di vista del design. Gli ingressi hash consentono una memoria, un archivio dati noto come tabella di hash, che è content-addressable (Hanlon, 1966; Knott , 1975) – anche una proprietà di alcuni tipi di reti neurali artificiali (Hopfield,1982; Kohonen et al., 1987). L’uso di una funzione hash crittografica significa che la posizione arbitraria in memoria di un ingresso è una funzione dell’ingresso stesso.
Abbiamo impiegato (usando la procedura sotto riportata) l’algoritmo crittografico sicuro di hash 1 (SHA-1), una funzione hash spesso usata, e l’abbiamo applicata ad ogni valore del vettore di input(National Institute of Standards and Technology, 2015). Due input molto simili (per esempio, membri della stessa categoria) sono estremamente improbabili che producano hash SHA-1 simili. Pertanto, essi saranno immagazzinati distalmente l’uno rispetto all’altro, e non sorgerà alcuna significativa correlazione all’interno della categoria (cioè, la fluidità funzionale è violata). In effetti, nelle applicazioni di crittografia tali similitudini potrebbero essere sfruttate per fare previsioni sull’input.
Se il codice neurale in un’area cerebrale fosse sostenuto da un comportamento simile a quello di una funzione hash, l’imaging non sarebbe in grado di rilevare le correlazioni con l’input. Ciò è dovuto al fatto che le funzioni hash sono ingegnerizzate in modo tale da distruggere qualsiasi correlazione, pur consentendo la memorizzazione dell’input in tabelle di hash.
Sebbene le tabelle di hash non sembrino ben assortite alle esigenze dei sistemi cognitivi che generalizzano gli input, esse si rivelerebbero utili in funzioni mentali di livello superiore come il monitoraggio della memoria di origine. Infatti, per prefigurare un risultato in basso, gli strati avanzati di reti neurali artificiali molto profonde approssimano una funzione di hash crittografica, il che rende di conseguenza difficile il recupero della struttura di somiglianza in quegli strati.
Modello
In questa sezione, consideriamo se le reti neurali con pesi casuali sono coerenti con il successo della fMRI, visti i suoi limiti nella misurazione dell’attività neurale. Le simulazioni della prossima sezione rivisitano questi aspetti attraverso l’obiettivo di un modello di apprendimento profondo addestrato a classificare fotografie di categorie del mondo reale, come ciclomotori, tigri, chitarre, pettirossi, ecc.
Ogni simulazione è analoga all’esecuzione di fMRI sul codice neurale candidato. Queste semplici simulazioni rispondono alla domanda se in linea di principio la somiglianza neurale può essere recuperata dai dati fMRI presi da certi schemi di codifica neurale. Gli stimoli sono presentati ad un modello mentre le sue rappresentazioni interne sono misurate da uno scanner fMRI simulato.
I metodi sono stati i seguenti. Gli stimoli sono costituiti da vettori 100-dimensionali che erano distorsioni di un prototipo sottostante. Poiché il rumore viene aggiunto al prototipo e il livello di distorsione aumenta, la somiglianza neurale (misurata usando il coefficiente di correlazione ρ di Pearson) tra il prototipo e il suo membro dovrebbe diminuire. La questione è se possiamo recuperare questo cambiamento nella somiglianza neurale nel nostro scanner fMRI simulato.
In primo luogo, ogni rete completamente collegata è stata inizializzata a pesi casuali disegnati da una distribuzione gaussiana (μ=0,σ=1). Poi, un prototipo è stato creato da 100 disegni da una distribuzione gaussiana (μ=0,σ=1).Diciannove distorsioni del prototipo sono state create aggiungendo livelli di rumore gaussiano con deviazione standard crescente (σ=σprev+0.05) al prototipo. Infine, ogni elemento è stato rinormalizzato e centrato mediamente, in modo che μ=0 e σ=1 indipendentemente dal livello di distorsione. Questa procedura è stata ripetuta per 100 reti casuali. Nelle simulazioni che seguono, i modelli considerati hanno coinvolto una parte della rete a 8 strati inizializzata in modo casuale (8×1002 pesi).
Gli schemi di codifica che seguono sono componenti importanti nei modelli di reti neurali artificiali. L’ordine di presentazione va dai componenti più elementari alle configurazioni più complesse delle reti. Per prefigurare i risultati mostrati nella Figura 2, la fMRI può recuperare la struttura di somiglianza per tutti questi modelli in varia misura, con i modelli più semplici che vanno molto meglio dei modelli più complessi.10.7554/eLife.21397.005Cifra 2.Man mano che i modelli diventano più complessi con l’aggiunta di strati, la struttura di somiglianza diventa più difficile da recuperare, il che potrebbe funzionare in parallelo lungo il flusso ventrale. (A)Per gli schemi di codifica delle reti neurali artificiali, la somiglianza con il prototipo cade con una distorsione crescente (ad es, I modelli, numerati 1-11, sono (1) codifica dello spazio vettoriale, (2) codifica del controllo del guadagno, (3) codifica della moltiplicazione della matrice, (4), codifica delpercotrone, (5) rete a 2 strati, (6) rete a 3 strati, (7) rete a 4 strati, (8) rete a 5 strati, (9) rete a 6 strati, (10) rete a 7 strati, e (11) rete a 8 strati.Più un modello è scuro, più il modello è semplice e più il modello conserva la struttura di somiglianza sotto fMRI. (B) Una rete neurale artificiale profonda e il flusso ventrale possono essere considerati come calcoli correlati. Come nei risultati della nostra simulazione, la somiglianza neurale dovrebbe essere più difficile da recuperare negli strati più avanzati.DOI:http://dx.doi.org/10.7554/eLife.21397.005
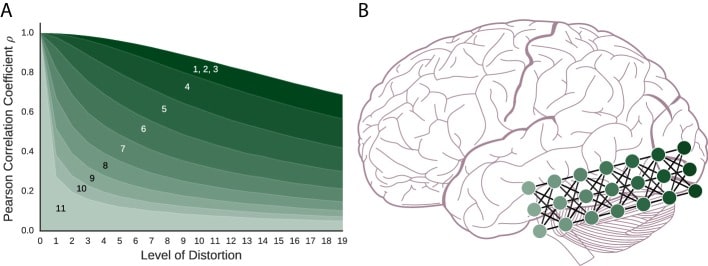
Figura 2.Man mano che i modelli diventano più complessi con l’aggiunta di strati, la struttura di somiglianza diventa più difficile da recuperare, che potrebbe funzionare in parallelo lungo il flusso ventrale.(A) Per gli schemi di codifica delle reti neurali artificiali, la somiglianza con il prototipo cade con una distorsione crescente (cioè I modelli, numerati 1-11, sono (1) codifica dello spazio vettoriale, (2) codifica del controllo del guadagno, (3) codifica della moltiplicazione della matrice, (4), codifica delpercotrone, (5) rete a 2 strati, (6) rete a 3 strati, (7) rete a 4 strati, (8) rete a 5 strati, (9) rete a 6 strati, (10) rete a 7 strati, e (11) rete a 8 strati.Più un modello è scuro, più il modello è semplice e più il modello conserva la struttura di somiglianza sotto fMRI. (B) Una rete neurale artificiale profonda e il flusso ventrale possono essere considerati come calcoli correlati. Come nei risultati della nostra simulazione, la somiglianza neurale dovrebbe essere più difficile da recuperare negli strati più avanzati.DOI:
http://dx.doi.org/10.7554/eLife.21397.005
Codifica spaziale vettoriale
Il primo di questa linea di modelli considerati è la codifica spaziale vettoriale (ℝn), in cui gli stimoli sono rappresentati come un vettore di caratteristiche reali. La rappresentazione di concetti in spazi multidimensionali ha una lunga storia di successo in psicologia (Shepard,1987). Ad esempio, in un grande spazio, i leoni e le tigri dovrebbero essere più vicini l’uno all’altro rispetto a leoni e pettirossi, perché sono più simili. I tipi di operazioni che vengono fatte naturalmente negli spazi vettoriali (ad esempio, aggiunte e moltiplicazioni) sono particolarmente adatti alla risposta BOLD. Ad esempio, la risposta emodinamica agli stimoli individuali si riassume approssimativamente attraverso una serie di condizioni (Dale e Buckner, 1997) e questa linearità sembra estendersi a modelli di rappresentazione (Reddy et al.,2009).
In questo schema di codifica neurale, ogni elemento (ad esempio, un cane) è rappresentato come l’insieme dei valori nel suo vettore di input (cioè, un insieme di numeri con intervallo [-1,1]). Ciò significa che per un dato stimolo, la rappresentazione che questo modello produce è identica all’input. In questo senso, la codifica dello spazio vettoriale è funzionalmente liscia in senso banale in quanto la funzione è identità. Come mostrato in Figura 2, la somiglianza neurale cade gradualmente con una distorsione aggiunta (cioè Pertanto, questo schema di codifica molto semplice crea spazi di rappresentazione che verrebbero rilevati con successo dalla fMRI.
Codifica del controllo del guadagno
Basato sul modello di base dello spazio vettoriale, questo schema codifica ogni vettore di input facendolo passare attraverso una funzione monotona non lineare, la funzione tangente iperbolica (tanh), che è funzionalmente liscia. Questo fa sì che ogni elemento vettore venga trasformato, o schiacciato, in valori compresi tra [-1,1].Tali funzioni sono richieste dalle reti neurali artificiali (e forse dal cervello) per il controllo del guadagno (Priebee Ferster, 2002). L’effetto pratico di questo modello è quello di spingere i valori nella rappresentazione interna del modello verso -1 o 1. Come si può vedere nella Figura 2, la somiglianza neurale è ben catturata dal modello di codifica neurale del controllo del guadagno.
Codifica della moltiplicazione della matrice
Questo modello esegue calcoli più sofisticati sugli stimoli in ingresso. In linea con il connessionismo precoce e la modellazione Rescorla-Wagner del condizionamento, questo modello riceve un vettore di ingresso ed esegue la moltiplicazione a matrice su di esso, cioè, calcola le somme ponderate degli input da trasmettere allo strato di uscita(Knapp e Anderson, 1984; Rescorla e Wagner, 1972). Queste semplici reti neurali monostrato possono essere sorprendentemente potenti e rappresentare una serie di risultati comportamentali complessi (Ramscaret al., 2013). Come vedremo nelle prossime sottosezioni, quando viene aggiunta una non linearità (ad esempio, tanh), le reti monostrato possono essere impilate l’una sull’altra per costruire reti profonde.
Questo schema di codifica neurale prende uno stimolo di input (ad esempio, l’immagine di un cane) e lo moltiplica per una matrice di peso per creare una rappresentazione interna, come mostrato in Figura 3. È interessante notare che, come mostrato nella Figura 3, la rappresentazione interna di questo schema di codifica è completamente priva di senso per l’occhio umano e non è super-voxel liscia, eppure conserva con successo la struttura di somiglianza (vedi Figura 2). La moltiplicazione della matrice mappa gli ingressi simili a rappresentazioni interne simili. In altre parole, il risultato non è super-voxel liscio, ma è funzionalmente liscio che congetturaamo sia fondamentale per il successo della fMRI.10.7554/eLife.21397.006Figure 3.The effect of matrix multiplication followed by the tanh function on the input stimulus. L’uscita di questa rete monostrato è mostrato, così come il risultato dell’applicazione di una non linearità all’uscita della moltiplicazione della matrice. In questo esempio, la scorrevolezza funzionale è preservata, mentre la scorrevolezza super-voxel non lo è. Il risultato dell’applicazione di questa non linearità può servire come input al livello successivo di una rete multistrato.DOI:http://dx.doi.org/10.7554/eLife.21397.006

Figura 3.L’effetto della moltiplicazione della matrice seguita dalla funzione tanh sullo stimolo di ingresso.Viene mostrato l’output di questa rete monostrato, così come il risultato dell’applicazione di una non linearità all’output della moltiplicazione della matrice. In questo esempio, la scorrevolezza funzionale è preservata, mentre la scorrevolezza super-voxel non lo è. Il risultato dell’applicazione di questa non linearità può servire come input al livello successivo di una rete multistrato.DOI:
http://dx.doi.org/10.7554/eLife.21397.006
Codifica Perceptron
Lo schema di codifica precedente era una rete neurale a singolo strato. Per creare reti multistrato, potenzialmente più potenti di una rete equivalente a singolo strato, è necessario aggiungere una non linearità (come il tanh) ad ogni strato di rete post-sinaptica.Qui, consideriamo una rete a singolo strato con la non-linearità tanh inclusa (vedi Figura 3). Come per la moltiplicazione a matrice in precedenza, questo schema di codifica neurale ha successo (vedi Figura 2) con “ingressi simili portano ad uscite simili” (Rummelhart et al.,1995, p. 31).
Codifica di rete neurale multistrato
La rete di base considerata nella sezione precedente può essere combinata con altre reti, creando una rete multistrato potenzialmente più potente. Questi modelli multistrato possono essere utilizzati per catturare un flusso di elaborazione come si pensa che avvenga per l’input visivo al flusso ventrale, mostrato in Figura 2B (DiCarloe Cox ,2007; Riesenhuber e Poggio, 1999, 2000; Quiroga et al., 2005; Yamins e DiCarlo, 2016).
In questa sezione si valuta se le proprietà di conservazione della somiglianza delle reti a singolo strato si estendono a reti più profonde, ma non ancora addestrate. Le simulazioni considerano reti da 2 a 8 strati. I modelli operano in modo identico al modello di codifica neurale del percetronio considerato nella sezione precedente.I percotroni sono impilati in modo tale che l’output di uno strato serve come input per lo strato successivo. Eseguiamo fMRI simulate solo sullo strato finale di ogni modello. Queste simulazioni considerano se le rappresentazioni che emergono in reti multistrato sono plausibili dato il successo della fMRI nello scoprire spazi di somiglianza vedi anche: (Cox et al.,2015; Cowell et al., 2009; Edelman et al., 1998; Goldrick, 2008; Laakso e Cottrell, 2000). Tali rappresentazioni, come si trovano nelle architetture di reti neurali artificiali profonde, vengono scoperte aggiungendo strati per scoprire aspetti comuni sempre più astratti tra gli input (Graves et al.,2013; Hinton et al., 2006; Hinton , 2007; Hinton et al., 2015; LeCun et al., 2015 ).
Come mostrato in Figura 2, più profonda è la rete, meno chiara diventa la struttura di somiglianza. Tuttavia, anche la rete più profonda conserva un certo livello di struttura di somiglianza. In effetti, man mano che si aggiungono gli strati, la fluidità funzionale diminuisce in modo tale che piccole perturbazioni all’input iniziale si traducono in rappresentazioni a strato finale che tendono a trovarsi in angoli arbitrari dello spazio rappresentazionale, in quanto l’output assume valori che sono +1 o -1 a causa del tanh.Con l’aggiunta di strati, la rete diventa potenzialmente più potente, ma meno liscia dal punto di vista funzionale, il che la rende meno adatta all’analisi tramite fMRI perché lo spazio di somiglianza si rompe. In altre parole, due stimoli simili possono generare quasi ortogonali (ad es, dissimili) rappresentazioni agli strati più avanzati di queste reti. Abbiamo misurato la fluidità funzionale per un ampio insieme di vettori di ingresso casuali utilizzando l’equazione 1 con la correlazione di Pearson che serve sia come misura di somiglianza che come misura di proporzionalità. Coerentemente con i risultati della Figura 2, allo strato 1 (equivalente al modello di codifica del percotrone) la scorrevolezza funzionale è stata di 0,86, ma è scesa a 0,22 dall’ottavo strato della rete. Questi valori sono stati calcolati utilizzando tutte le coppie di item che consistono di un prototipo e di una delle sue distorsioni. Nella sezione Discussione, consideriamo il significato teorico di questi risultati in tandem con i risultati della rete di apprendimento profondo (sezione successiva).
Reti di apprendimento profondo
Le reti di apprendimento profondo (DLN) hanno portato ad una rivoluzione nel machine learning e nell’intelligenza artificiale(Krizhevsky et al., 2012; LeCun et al., 1998; Serre et al., 2007; Szegedy et al., 2015a). Le DLN superano gli approcci esistenti sui compiti di riconoscimento degli oggetti formando complesse reti multistrato con milioni di parametri (ad es, Recentemente, i neuroscienziati si sono interessati a come i calcoli e le rappresentazioni di questi modelli si riferiscono al flusso ventrale nelle scimmie e negli esseri umani (Cadieu et al.,2014; Dubois et al. , 2015; Guclu e van Gerven, 2015; Hong et al., 2016; Khaligh-Razavi e Kriegeskorte, 2014; Yamins et al., 2014; Yamins e DiCarlo, 2016). Per questi motivi, abbiamo scelto di esaminare questi modelli, che consentono anche la RSA a più livelli di rappresentazione.
In questo contributo, una questione chiave è se la scorrevolezza funzionale si disgreghi a livelli più avanzati nei DLN come ha fatto nelle reti neurali casuali non addestrate considerate nella sezione precedente. Affrontiamo questa domanda presentando stimoli di immagini naturali (cioè fotografie inedite) a un DLN addestrato, in particolare Inception-v3 GoogLeNet(Szegedy et al., 2015b), e applicando la RSA per valutare se la struttura di somiglianza degli elementi sarebbe recuperabile utilizzando la fMRI.
Architettura
La DLN che consideriamo, Inception-v3 GoogLeNet, è una rete neurale convoluzionale (CNN), che è un tipo di DLN particolarmente abile nella classificazione e nel riconoscimento degli ingressi visivi. Le CNN eccellono nella visione artificiale, imparando da enormi quantità di dati. Per esempio, l’accuratezza simile a quella umana sui set di test è stata raggiunta da: LeNet, una CNN pionieristica che identifica le cifre scritte a mano (LeCun etal., 1998); HMAX, addestrata a rilevare oggetti, ad esempio volti, in ambienti disordinati (Serre et al.,2007); e AlexNet, che classifica le fotografie in 1000 categorie (Krizhevsky et al.,2012).
L’architettura di alto livello delle CNN è costituita da molti strati(Szegedy et al., 2015a), sovrapposti l’uno sull’altro, più o meno come i percotroni multilivello impilati descritti in precedenza. Una differenza fondamentale è che le CNN hanno una maggiore varietà soprattutto nell’ampiezza (numero di unità) tra gli strati.
In molte CNN, alcuni degli strati della rete sono convoluzionali, che contengono componenti che non ricevono input dall’intero strato precedente, ma da un piccolo sottoinsieme di esso (Szegedyet al., 2015b). Molti componenti convoluzionali sono necessari per processare l’intero strato precedente creando una sovrapposizione di piccoli patch. Spesso gli strati convoluzionali sono interleaved con strati di max-pooling (Lecun et al., Questo tipo di elaborazione e di architettura è sia empiricamente guidato da ciò che funziona meglio, sia ispirato dal flusso visivo ventrale, in particolare dai campi ricettivi (Fukushima, 1980; Hubel e Wiesel, 1959, 1968; Serre et al., 2007).
Gli strati voluzionali e di max-pooling forniscono una struttura che è intrinsecamente gerarchica. Gli strati più bassi eseguono calcoli su piccole patch localizzate dell’input, mentre gli strati più profondi eseguono calcoli su aree sempre più grandi, più globali, degli stimoli. Dopo tale elaborazione localizzata, è tipico includere strati che sono completamente connessi, cioè, sono più classicamente connessionisti. E infine, uno strato con la struttura di output richiesta, ad esempio, unità che rappresentano classi o una risposta sì/no, a seconda dei casi.
Inception-v3 GoogLeNet utilizza una disposizione specifica di questi strati, collegati sia in serie che in parallelo(Szegedy et al., 2015b, 2015a, 2016). In totale ha 26 strati e 25 milioni di parametri, inclusi i pesi di connessione (Szegedyet al., Lo strato finale è uno strato softmax che viene addestrato ad attivare una singola unità per classe. Queste unità corrispondono alle etichette che sono state applicate a set di fotografie dall’uomo, ad esempio, ‘space shuttle’, ‘gelato’, ‘calza’, all’interno del database ImageNet (Russakovsky et al.,2015).
Inception-v3 GoogLeNet è stato addestrato su milioni di fotografie a marchio umano provenienti da 1.000 set fotografici di ImageNet (set di fotografie). L’output di 1.000 unità prodotte dalla rete quando viene presentato con una fotografia rappresenta le probabilità dell’input appartenente a ciascuna di queste classi.Per esempio, se alla rete viene data una fotografia di un ciclomotore può anche attivare l’unità di uscita che corrisponde alla bicicletta con attivazione 0.03. Questo viene interpretato come la rete che esprime la convinzione che ci sia una probabilità del 3% che l’etichetta appropriata per l’ingresso sia “bicicletta”.Inoltre, questa interpretazione è utile perché consente la coesistenza di più classi all’interno di un singolo ingresso: ad esempio, una foto con una ghigliottina e una parrucca all’interno di essa farà sì che si attivino entrambe le unità di uscita corrispondenti.Così si ritiene che la rete abbia imparato una distribuzione di etichette appropriate che riflettono gli elementi più salienti di una scena. Inception-v3 GoogLeNet, raggiunge livelli umani di accuratezza sui set di prova, producendo l’etichetta corretta nelle sue cinque ipotesi più probabili circa il 95% del tempo (Szegedy etal., 2015b).
Simulazione di rete di apprendimento profondo
Valutiamo se la fluidità funzionale diminuisce man mano che gli input vengono elaborati dai livelli più avanzati di Inception-v3 GoogLeNet. Se così fosse, la fMRI dovrebbe avere meno successo nelle regioni cerebrali che istanziano calcoli analoghi ai livelli più avanzati di tali reti. A differenza delle precedenti simulazioni, noi presentiamo a queste reti nuove fotografie di categorie naturali. La domanda chiave è se gli elementi di categorie correlate (ad esempio, banjo e chitarre) saranno simili a vari strati di rete. Le 40 fotografie (cioè gli stimoli) sono suddivise in parti uguali in 8 categorie subordinate: banjo, chitarre, ciclomotori, auto sportive, leoni, tigri, pettirossi e pernici, che a loro volta si aggregano in 4 categorie di livello base: strumenti musicali, veicoli, mammiferi e uccelli; che a loro volta si aggregano in 2 categorie sovraordinate: animati e inanimati.
Consideriamo quanto siano simili le rappresentazioni interne della rete per le coppie di stimoli, confrontando l’attività di rete risultante, che è analoga al confronto dell’attività neurale sui voxel nella RSA. Le correlazioni per tutti i possibili accoppiamenti dei 40 stimoli sono state calcolate sia per uno strato di rete medio che per uno strato successivo (vedi Figura 4).10.7554/eLife.21397.007Figure 4.Similarity structure diventa più difficile da recuperare negli strati più avanzati del DLN.(A) La struttura di similarità in uno strato intermedio di un DLN, Inception-v3 GoogLeNet. I mammiferi (leoni e tigri) e gli uccelli (pettirossi e pernici) si correlano formando un dominio di alto livello, rendendo il quadrante superiore sinistro una tonalità più scura di rosso. Mentre i veicoli (auto sportive e ciclomotori) e gli strumenti musicali (chitarre e banjo) formano due categorie di alto livello. (B) Al contrario, in uno strato successivo di questa rete, lo spazio di somiglianza mostra elevate correlazioni all’interno delle categorie e correlazioni indebolite tra le categorie. Mentre una certa struttura tra le categorie è preservata, i ciclomotori non sono più simili alle auto sportive di quanto lo siano ai pettirossi.DOI:http://dx.doi.org/10.7554/eLife.21397.007
Lo strato intermedio(Figura 4A) rivela una somiglianza di categoria incrociata sia a livello di base che di sovraordinata. Ad esempio, i leoni sono più simili ai pettirossi che alle chitarre, ma nel livello successivo (Figura 4B) la struttura di somiglianza si è scomposta in modo tale che la somiglianza di categoria subordinata domina (cioè, Un leone è come un altro leone, ma non tanto come una tigre). È interessante notare che il declino della scorrevolezza funzionale non è una conseguenza della scarsità nello strato successivo come il coefficiente di Gini, una misura della scarsità (Gini,1909), è 0,947 per lo strato intermedio precedente (Figura 4A) e 0,579 per lo strato avanzato successivo (Figura 4B), indicando che le rappresentazioni di rete sono distribuite in generale e ancora di più nello strato successivo. Pertanto, il declino della fluidità funzionale negli strati successivi non sembra essere una semplice conseguenza dell’addestramento di queste reti per classificare gli stimoli, anche se sarebbe interessante fare un confronto con approcci non supervisionati che possono funzionare a livelli di precisione equivalenti (attualmente non esiste una rete di questo tipo).
Questi risultati DLN sono direttamente analoghi a quelli di reti casuali non addestrate (vedi Figura 2). In queste simulazioni, modelli di input simili mappati a rappresentazioni interne ortogonali (cioè dissimili) in strati successivi. Allo stesso modo, il DLN addestrato in strati successivi può catturare la struttura di somiglianza solo all’interno di categorie subordinate (ad esempio, il DLN addestrato in strati successivi può catturare la struttura di somiglianza solo all’interno di categorie subordinate, una tigre è come un’altra tigre) che la rete è stata addestrata a classificare. L’effetto dell’addestramento della rete è stato quello di creare classi di equivalenza basate sull’etichetta di addestramento (ad es, Violando la fluidità funzionale, tutte le altre strutture di somiglianza vengono scartate in modo tale che una tigre non sia più simile a un leone che a un banjo dal punto di vista della rete. Se le regioni cerebrali dovessero operare in modo simile, la fMRI non riuscirebbe a recuperare la struttura di somiglianza. Nella Discussione, consideriamo le implicazioni di questi risultati sulla nostra comprensione del flusso ventrale e le prospettive per la fMRI.
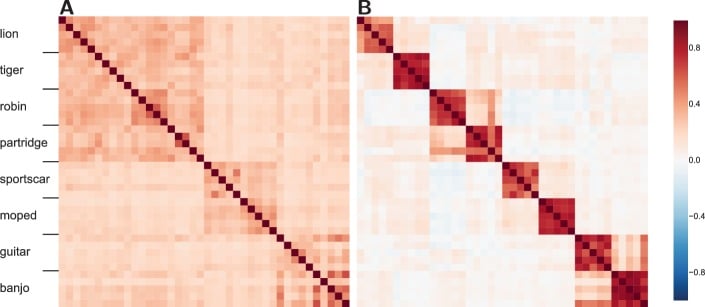
Figura 4.La struttura di somiglianza diventa più difficile da recuperare negli strati più avanzati del DLN.(A) La struttura di somiglianza in uno strato intermedio di un DLN, Inception-v3 GoogLeNet. I mammiferi (leoni e tigri) e gli uccelli (pettirossi e pernici) si correlano formando un dominio di alto livello, rendendo il quadrante superiore sinistro una tonalità più scura di rosso. Mentre i veicoli (auto sportive e ciclomotori) e gli strumenti musicali (chitarre e banjo) formano due categorie di alto livello. (B) Al contrario, in uno strato successivo di questa rete, lo spazio di somiglianza mostra elevate correlazioni all’interno delle categorie e correlazioni indebolite tra le categorie. Mentre una certa struttura tra le categorie è preservata, i ciclomotori non sono più simili alle auto sportive di quanto lo siano ai pettirossi.DOI:
http://dx.doi.org/10.7554/eLife.21397.007
Discussione
I neuroscienziati preferirebbero giustamente un metodo che avesse sia un’eccellente risoluzione spaziale che temporale per misurare l’attività cerebrale. Tuttavia, come dimostriamo in questo articolo, il fatto che la fMRI si sia dimostrata utile nell’esame delle rappresentazioni neurali, nonostante i limiti della sua risoluzione sia temporale che spaziale, dice qualcosa sulla natura del codice neurale. Una conclusione generale è che il codice neurale deve essere liscio, sia a livello voxel (tale che le risposte voxel sono disomogenee nel tempo e nello spazio) che funzionale.
Quest’ultima nozione di fluidità è spesso trascurata o confusa con quella di super-voxel, ma è necessaria affinché la fMRI recuperi gli spazi di somiglianza nel cervello. Gli schemi di codifica, come la codifica fattoriale e l’hash, sono utili in numerose applicazioni del mondo reale e hanno una funzione inversa (cioè, si può andare indietro dalla rappresentazione interna per recuperare l’input di stimolo unico). Tuttavia, questi schemi sono incompatibili con il successo della fMRI perché non sono funzionalmente lisci. Per esempio, se il cervello utilizzasse esclusivamente tali schemi di codifica, la rappresentazione neurale di un pettirosso non sarebbe più simile a quella di un passero che a quella di un’automobile. Il fatto che tali somiglianze neurali siano recuperabili dalla fMRI suggerisce che il codice neurale differisce da questi schemi in molti casi.
Al contrario, abbiamo scoperto che i tipi di rappresentazioni usate e generate dalle reti neurali artificiali, incluse le reti di apprendimento profondo, sono ampiamente compatibili con il successo della fMRI nella valutazione delle rappresentazioni neurali. Questi schemi di codifica sono funzionalmente lisci in quanto input simili tendono verso output simili, il che permette di riflettere la somiglianza degli item nella somiglianza neurale (misurata dalla fMRI). Tuttavia, abbiamo scoperto che la fluidità funzionale si interrompe quando vengono aggiunti ulteriori strati di rete. In particolare, abbiamo dimostrato che le reti multistrato alla fine convergono verso qualcosa di simile a una funzione hash, in quanto le posizioni arbitrarie nella memoria corrispondono a categorie di ingressi.
Questi risultati assumono un significato aggiuntivo dato il recente interesse per le reti neurali artificiali profonde come conti computazionali del flusso ventrale. Una visione emergente è che più avanzati sono gli strati di questi modelli, più gli strati corrispondono a regioni più avanzate lungo il flusso ventrale (Cadieuet al., 2014-12; Dubois et al., 2015; Guclu e van Gerven, 2015; Hong et al., 2016; Khaligh-Razavi e Kriegeskorte, 2014; Yamins et al., 2014; Yamins e DiCarlo, 2016).
Se questo punto di vista è corretto, i nostri risultati indicano che le rappresentazioni neurali dovrebbero progressivamente diventare meno lisce dal punto di vista funzionale e più astratte man mano che ci si muove lungo il flusso ventrale (si veda la Figura 2). Infatti, le rappresentazioni neurali sembrano diventare più astratte, codificando interi concetti o categorie, in funzione di quanto lontano lungo il flusso ventrale si trovano (Braccie Op de Beeck, 2016; DiCarlo e Cox, 2007; Riesenhuber e Poggio, 1999, 2000; Yamins e DiCarlo, 2016).Ad esempio, nelle prime fasi dell’elaborazione visiva, il cervello può estrarre le cosiddette caratteristiche di base, come ad esempio nelle colonne di orientamento ampiamente sintonizzate (Hubele Wiesel, 1959, 1968). Al contrario, più tardi nell’elaborazione, le cellule possono rispondere selettivamente a particolari classi di stimoli individuali, ad esempio, Jennifer Aniston, nonna, concetto, o cellule gnostiche(Gross, 2002; Konorski, 1967; Quiroga et al., 2005), indipendentemente dall’orientamento, ecc.
Allo stesso modo, abbiamo scoperto che le rappresentazioni di Inception-v3 GoogLeNet sono diventate simili a simboli a livelli di rete avanzati, in modo tale che gli oggetti che condividono un’etichetta di categoria (ad es, Le nostre simulazioni di reti casuali hanno anche trovato una ridotta fluidità funzionale a livelli di rete avanzati, suggerendo una proprietà geometrica di base delle reti multistrato. L’effetto dell’addestramento sembra limitato alla creazione di stati di rete in cui gli stimoli che condividono la stessa etichetta (es, punti di vista multipli di Jennifer Aniston) diventano simili e gli elementi di tutte le altre categorie (anche se concettualmente correlati) diventano ortogonali. In tal caso, le aree più lontane lungo il flusso ventrale dovrebbero risultare meno favorevoli all’imaging (si veda la Figura 2). Infatti, un recente studio sul riconoscimento degli oggetti ha scoperto che il soffitto sui valori di correlazione osservabili diventa più basso man mano che ci si muove lungo il flusso ventrale (Bracci eOp de Beeck, 2016).
Qui, ci siamo concentrati sull’uso della fMRI per recuperare gli spazi di somiglianza non degenerativi (cioè dove ci sono somiglianze al di là delle autosimiltà). Tuttavia, la fluidità funzionale è importante anche per altri approcci di analisi. Ad esempio, i decodificatori MVPA addestrati a classificare gli oggetti (ad esempio, viene mostrata una casa o un volto?) sulla base dell’attività della fMRI si generalizzeranno a nuovi stimoli solo quando la fluidità funzionale regge. Allo stesso modo, i cluster univariati (ad esempio, una casa o un’area del volto) saranno probabilmente trovati e generalizzati a nuovi stimoli quando la fluidità funzionale regge, perché la fluidità funzionale implica profili di attivazione simili per stimoli simili. La scorrevolezza funzionale dovrebbe essere un fattore importante per determinare le prestazioni dei classificatori e la solidità statistica dei cluster univariati di voxel.
Nella scienza cognitiva, la ricerca è spesso divisa in livelli di analisi. Nei livelli di Marr, il livello superiore è la descrizione del problema, il livello intermedio cattura come il problema viene risolto, e il livello inferiore riguarda come la soluzione viene implementata nel cervello (Marr,1982). Dato che il “come” e il “dove” della cognizione sembrano fondersi, alcuni hanno messo in dubbio l’utilità di questa divisione tripartita (Love, 2015).
I nostri risultati suggeriscono un’altra inadeguatezza di questi tre livelli di descrizione, vale a dire che il livello di implementazione stesso dovrebbe essere ulteriormente suddiviso. Ciò che viene misurato dalla fMRI è su una scala molto più astratta di ciò che può essere misurato nel cervello.Per esempio, gli sforzi maggiori, come il progetto europeo Human Brain Project e il progetto Machine Intelligence from Cortical Networks (Underwood,2016), riguardano principalmente gli aspetti del cervello a grana fine che sono al di fuori della portata della fMRI (Chi,2016; Frégnac e Laurent, 2014). Allo stesso modo, i modelli di neuroni a picco, ad esempio,(Wong e Wang, 2006) sono a un livello di analisi inferiore a quello in cui si applica la fMRI.
Tuttavia, la fMRI si è dimostrata utile per comprendere le rappresentazioni neurali che sono conseguenti al comportamento. Forse questo successo suggerisce che il livello appropriato per mettere in relazione il cervello con il comportamento è vicino a ciò che la fMRI misura. Questo non significa che gli sforzi di livello inferiore non abbiano utilità quando i dettagli sono di interesse.Tuttavia, il successo della fMRI potrebbe significare che quando si è interessati alla natura dei calcoli effettuati dal cervello, si può preferire il livello di analisi in cui si applica la fMRI. Per fare un’analogia, si potrebbe costruire una teoria della macroeconomia basata sulla fisica quantistica, ma sarebbe incredibilmente macchinosa e non più predittiva né esplicativa di una teoria che contenesse concetti astratti come il denaro e l’offerta. Il riduzionismo, pur essendo seducente, non è sempre la strada migliore da seguire.
References
- Adrian ED. The impulses produced by sensory nerve endings: Part I. The Journal of Physiology. 1926; 61:49-72. DOI | PubMed
- Alink A, Krugliak A, Walther A, Kriegeskorte N. fMRI orientation decoding in V1 does not require global maps or globally coherent orientation stimuli. Frontiers in Psychology. 2013; 4DOI | PubMed
- Ances BM, Liang CL, Leontiev O, Perthen JE, Fleisher AS, Lansing AE, Buxton RB. Effects of aging on cerebral blood flow, oxygen metabolism, and blood oxygenation level dependent responses to visual stimulation. Human Brain Mapping. 2009; 30:1120-1132. DOI | PubMed
- Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nature Reviews Neuroscience. 2006; 7:358-366. DOI | PubMed
- Binder JR, Frost JA, Hammeke TA, Cox RW, Rao SM, Prieto T. Human brain language areas identified by functional magnetic resonance imaging. Journal of Neuroscience. 1997; 17:353-362. PubMed
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. Journal of Neuroscience. 1996; 16:4207-4221. PubMed
- Bracci S, Op de Beeck H. Dissociations and associations between shape and category representations in the two visual pathways. Journal of Neuroscience. 2016; 36:432-444. DOI | PubMed
- Cadieu CF, Hong H, Yamins DL, Pinto N, Ardila D, Solomon EA, Majaj NJ, DiCarlo JJ. Deep neural networks rival the representation of primate IT cortex for core visual object recognition. PLoS Computational Biology. 2014; 10DOI | PubMed
- Carp J. The secret lives of experiments: methods reporting in the fMRI literature. NeuroImage. 2012; 63:289-300. DOI | PubMed
- Chaimow D, Yacoub E, Ugurbil K, Shmuel A. Modeling and analysis of mechanisms underlying fMRI-based decoding of information conveyed in cortical columns. NeuroImage. 2011; 56:627-642. DOI | PubMed
- Chi KR. Neural modelling: Abstractions of the mind. Nature. 2016; 531:S16-S17. DOI | PubMed
- Cowell RA, Huber DE, Cottrell GW. Virtual brain reading: A connectionist approach to understanding fMRI. 2009.
- Cox CR, Seidenberg MS, Rogers TT. Connecting functional brain imaging and parallel distributed processing. Language, Cognition and Neuroscience. 2015; 30:380-394. DOI
- Cox DD, Savoy RL. Functional magnetic resonance imaging (fMRI) "brain reading": detecting and classifying distributed patterns of fMRI activity in human visual cortex. NeuroImage. 2003; 19:261-270. DOI | PubMed
- Dale AM, Buckner RL. Selective averaging of rapidly presented individual trials using fMRI. Human Brain Mapping. 1997; 5:329-340. DOI | PubMed
- Davatzikos C, Ruparel K, Fan Y, Shen DG, Acharyya M, Loughead JW, Gur RC, Langleben DD. Classifying spatial patterns of brain activity with machine learning methods: application to lie detection. NeuroImage. 2005; 28:663-668. DOI | PubMed
- Davis T, Xue G, Love BC, Preston AR, Poldrack RA. Global neural pattern similarity as a common basis for categorization and recognition memory. Journal of Neuroscience. 2014; 34:7472-7484. DOI | PubMed
- De Martino F, Valente G, Staeren N, Ashburner J, Goebel R, Formisano E. Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. NeuroImage. 2008; 43:44-58. DOI | PubMed
- DiCarlo JJ, Cox DD. Untangling invariant object recognition. Trends in Cognitive Sciences. 2007; 11:333-341. DOI | PubMed
- Dubois J, de Berker AO, Tsao DY. Single-unit recordings in the macaque face patch system reveal limitations of fMRI MVPA. Journal of Neuroscience. 2015; 35:2791-2802. DOI | PubMed
- Edelman S, Grill-Spector K, Kushnir T, Malach R. Toward direct visualization of the internal shape representation space by fMRI. Psychobiology. 1998; 26:309-321.
- Fano U. Ionization yield of radiations. II. The fluctuations of the number of ions. Physical Review. 1947; 72:26-29. DOI
- Freeman J, Brouwer GJ, Heeger DJ, Merriam EP. Orientation decoding depends on maps, not columns. Journal of Neuroscience. 2011; 31:4792-4804. DOI | PubMed
- Frégnac Y, Laurent G. Neuroscience: Where is the brain in the human brain project?. Nature. 2014; 513:27-29. DOI | PubMed
- Fukushima K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics. 1980; 36:193-202. DOI | PubMed
- Gini C. Il diverso accrescimento delle classi sociali e la concentrazione della ricchezza. Giornale Degli Economisti. 1909; 38:27-83.
- Goldrick M. Does like attract like? Exploring the relationship between errors and representational structure in connectionist networks. Cognitive Neuropsychology. 2008; 25:287-313. DOI | PubMed
- Graves A, Mohamed A, Hinton G. Speech recognition with deep recurrent neural networks. 2013;6645-6649. DOI
- Gross CG. Genealogy of the "grandmother cell". The Neuroscientist. 2002; 8:512-518. DOI | PubMed
- Güçlü U, van Gerven MA. Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream. Journal of Neuroscience. 2015; 35:10005-10014. DOI | PubMed
- Hanlon AG. Content-Addressable and associative memory systems a survey. IEEE Transactions on Electronic Computers. 1966; EC-15:509-521. DOI
- Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network. arXiv. 2015. Publisher Full Text
- Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Computation. 2006; 18:1527-1554. DOI | PubMed
- Hinton GE. Learning multiple layers of representation. Trends in Cognitive Sciences. 2007; 11:428-434. DOI | PubMed
- Hong H, Yamins DL, Majaj NJ, DiCarlo JJ. Explicit information for category-orthogonal object properties increases along the ventral stream. Nature Neuroscience. 2016; 19:613-622. DOI | PubMed
- Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. PNAS. 1982; 79:2554-2558. DOI | PubMed
- Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat’s striate cortex. The Journal of Physiology. 1959; 148:574-591. DOI | PubMed
- Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. The Journal of Physiology. 1968; 195:215-243. DOI | PubMed
- Huettel SA, Song AW, McCarthy G, Huettel SA, Song AW, McCarthy G. Functional Magnetic Resonance Imaging. Sunauer Associates; 2009.
- Kamitani Y, Tong F. Decoding the visual and subjective contents of the human brain. Nature Neuroscience. 2005; 8:679-685. DOI | PubMed
- Katz SM. Distribution of content words and phrases in text and language modelling. Natural Language Engineering. 1996; 2:15-59. DOI
- Khaligh-Razavi SM, Kriegeskorte N. Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Computational Biology. 2014; 10DOI | PubMed
- Knapp AG, Anderson JA. Theory of categorization based on distributed memory storage. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984; 10:616-637. DOI
- Knott GD. Hashing functions. The Computer Journal. 1975; 18:265-278. DOI
- Kohonen T, Huang TS, Schroeder MR. Content-Addressable Memories. Springer-Verlag; 1987. DOI
- Konorski J. Integrative Activity of the Brain. University of Chicago Press; 1967.
- Kriegeskorte N, Cusack R, Bandettini P. How does an fMRI voxel sample the neuronal activity pattern: compact-kernel or complex spatiotemporal filter?. NeuroImage. 2010; 49:1965-1976. DOI | PubMed
- Kriegeskorte N, Mur M, Bandettini P. Representational similarity analysis – connecting the branches of systems neuroscience. Frontiers in Systems Neuroscience. 2008; 2DOI | PubMed
- Kriegeskorte N. Relating population-code representations between man, monkey, and computational models. Frontiers in Neuroscience. 2009; 3:363-373. DOI | PubMed
- Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. 2012;1097-1105.
- Laakso A, Cottrell G. Content and cluster analysis: Assessing representational similarity in neural systems. Philosophical Psychology. 2000; 13:47-76. DOI
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015; 521:436-444. DOI | PubMed
- Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998; 86:2278-2324. DOI
- Logothetis NK. The neural basis of the blood-oxygen-level-dependent functional magnetic resonance imaging signal. Philosophical Transactions of the Royal Society B: Biological Sciences. 2002; 357:1003-1037. DOI
- Logothetis NK. What we can do and what we cannot do with fMRI. Nature. 2008; 453:869-878. DOI | PubMed
- Love BC. The algorithmic level is the bridge between computation and brain. Topics in Cognitive Science. 2015; 7:230-242. DOI | PubMed
- Mack ML, Preston AR, Love BC. Decoding the brain’s algorithm for categorization from its neural implementation. Current Biology. 2013; 23:2023-2027. DOI | PubMed
- Mack ML, Preston AR. Decisions about the past are guided by reinstatement of specific memories in the hippocampus and perirhinal cortex. NeuroImage. 2016; 127:144-157. DOI | PubMed
- Magri C, Schridde U, Murayama Y, Panzeri S, Logothetis NK. The amplitude and timing of the BOLD signal reflects the relationship between local field potential power at different frequencies. Journal of Neuroscience. 2012; 32:1395-1407. DOI | PubMed
- Marr D. Vision: A Computational Investigation Into the Human Representation and Processing of Visual Information. Henry Holt and Co., Inc: New York, USA; 1982.
- Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. Journal of Neurophysiology. 1983; 49:1127-1147. PubMed
- Mitchell TM, Hutchinson R, Niculescu RS, Pereira F, Wang X, Just M, Newman S. Learning to decode cognitive states from brain images. Machine Learning. 2004; 57:145-175. DOI
- National Institute of Standards and Technology. Secure Hash Standard (SHS) (Standard No. 180). FIPS PUB: Gaithersburg, USA; 2015.
- Nevado A, Young MP, Panzeri S. Functional imaging and neural information coding. NeuroImage. 2004; 21:1083-1095. DOI | PubMed
- Norman KA, Polyn SM, Detre GJ, Haxby JV. Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends in Cognitive Sciences. 2006; 10:424-430. DOI | PubMed
- O’Herron P, Chhatbar PY, Levy M, Shen Z, Schramm AE, Lu Z, Kara P. Neural correlates of single-vessel haemodynamic responses in vivo. Nature. 2016; 534:378-382. DOI | PubMed
- Panzeri S, Macke JH, Gross J, Kayser C. Neural population coding: combining insights from microscopic and mass signals. Trends in Cognitive Sciences. 2015; 19:162-172. DOI | PubMed
- Pessoa L, Gutierrez E, Bandettini P, Ungerleider L. Neural correlates of visual working memory: fMRI amplitude predicts task performance. Neuron. 2002; 35:975-987. PubMed
- Pouget A, Dayan P, Zemel R. Information processing with population codes. Nature Reviews. Neuroscience. 2000; 1:125-132. DOI | PubMed
- Priebe NJ, Ferster D. A new mechanism for neuronal gain control (or how the gain in brains has mainly been explained). Neuron. 2002; 35:602-604. DOI | PubMed
- Quiroga RQ, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single neurons in the human brain. Nature. 2005; 435:1102-1107. DOI | PubMed
- Ramscar M, Dye M, Klein J. Children value informativity over logic in word learning. Psychological Science. 2013; 24:1017-1023. DOI | PubMed
- Reddy L, Kanwisher NG, VanRullen R. Attention and biased competition in multi-voxel object representations. PNAS. 2009; 106:21447-21452. DOI | PubMed
- Rescorla RA, Wagner AR. Appleton-Century-Crofts. 1972.
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nature Neuroscience. 1999; 2:1019-1025. DOI | PubMed
- Riesenhuber M, Poggio T. Models of object recognition. Nature Neuroscience. 2000; 3 Suppl:1199-1204. DOI | PubMed
- Rummelhart DE, Durbin R, Golden R, Chauvin Y. Backpropagation: Theory, Architectures, and Applications. Lawrence Erlbaum associates Associates Inc: USA; 1995.
- Russakovsky O, Deng J, Su H, Krause J, Satheesh S, Ma S, Huang Z, Karpathy A, Khosla A, Bernstein M, Berg AC, Fei-Fei L. ImageNet large scale visual recognition challenge. International Journal of Computer Vision. 2015; 115:211-252. DOI
- Scheeringa R, Fries P, Petersson KM, Oostenveld R, Grothe I, Norris DG, Hagoort P, Bastiaansen MC. Neuronal dynamics underlying high- and low-frequency EEG oscillations contribute independently to the human BOLD signal. Neuron. 2011; 69:572-583. DOI | PubMed
- Serre T, Poggio T. A neuromorphic approach to computer vision. Communications of the ACM. 2010; 53:54-61. DOI
- Serre T, Wolf L, Bileschi S, Riesenhuber M, Poggio T. Robust object recognition with Cortex-Like mechanisms. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2007-03; 29:411-426. DOI | PubMed
- Shepard RN. Toward a universal law of generalization for psychological science. Science. 1987; 237:1317-1323. DOI | PubMed
- Swisher JD, Gatenby JC, Gore JC, Wolfe BA, Moon CH, Kim SG, Tong F. Multiscale pattern analysis of orientation-selective activity in the primary visual cortex. Journal of Neuroscience. 2010; 30:325-330. DOI | PubMed
- Szegedy C, Ioffe S, Vanhoucke V. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. abs/1602.07261. 2016.
- Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. 2015a. DOI
- Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z. Rethinking the inception architecture for computer vision. abs/1512.00567. 2015b.
- Tompary A, Duncan K, Davachi L. High-resolution investigation of memory-specific reinstatement in the hippocampus and perirhinal cortex. Hippocampus. 2016; 26:995-1007. DOI | PubMed
- Turner R. How much cortex can a vein drain? Downstream dilution of activation-related cerebral blood oxygenation changes. NeuroImage. 2002; 16:1062-1067. DOI | PubMed
- Underwood E. Barcoding the brain. Science. 2016; 351:799-800. DOI | PubMed
- Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. Journal of Neuroscience. 2006; 26:1314-1328. DOI | PubMed
- Yamins DL, DiCarlo JJ. Using goal-driven deep learning models to understand sensory cortex. Nature Neuroscience. 2016; 19:356-365. DOI | PubMed
- Yamins DL, Hong H, Cadieu CF, Solomon EA, Seibert D, DiCarlo JJ. Performance-optimized hierarchical models predict neural responses in higher visual cortex. PNAS. 2014; 111:8619-8624. DOI | PubMed
Fonte
Guest O, Love BC, Poldrack R () What the success of brain imaging implies about the neural code. eLife 6e21397. https://doi.org/10.7554/eLife.21397





