Abstract
Introduzione
La ricerca sui microbiota incarna oggi la natura ricca di dati della biologia moderna. I progressi nel sequenziamento del DNA ad alto rendimento consentono di effettuare indagini rapide e convenienti su migliaia di taxa batterici in centinaia di campioni(Caporaso et al., 2011). L’esplosiva disponibilità di dati di sequenziamento ha messo in bilico la ricerca sui microbiota per far progredire la nostra comprensione di campi così diversi come l’ecologia, l’evoluzione, la medicina e l’agricoltura(Waldor et al., 2015). Un notevole sforzo si concentra ora sull’interrogatorio di insiemi di dati sui microbioti per identificare le relazioni tra i taxa batterici, così come tra i microbi e il loro ambiente.
È sempre più apprezzato che la natura relativa dei dati sull’abbondanza microbica negli studi sui microbioti possa portare ad analisi statistiche spurie(Jackson, 1997; Friedman e Alm, 2012; Aitchison, 1986; Lovell et al., 2011; Gloor et al., 2016a; Britanova et al., 2014; Li, 2015; Tsilimigras e Fodor, 2016). Con il sequenziamento di prossima generazione, il numero di letture per campione può variare indipendentemente dalla carica microbica(Lovell et al., 2011; Tsilimigras e Fodor, 2016). Al fine di rendere le misurazioni comparabili tra i campioni, la maggior parte degli studi analizza quindi l’abbondanza relativa dei taxa batterici. Le analisi non vengono quindi effettuate sulle abbondanze assolute dei membri della comunità(Figura 1A), ma piuttosto su dati relativi che occupano uno spazio geometrico limitato e sono rappresentati in un sistema di coordinate non cartesiano(Figura 1B). Tali insiemi di dati di abbondanza relativa sono spesso definiti composizionali. L’uso della maggior parte degli strumenti statistici standard( ad esempio, correlazione, regressione o classificazione) all’interno di uno spazio composizionale porta a risultati spuri(Pawlowsky-Glahn et al., 2015). Ad esempio, tre quarti delle interazioni batteriche significative dedotte dalla correlazione di Pearson su un set di dati composizionali di microbiota umani erano probabilmente false(Friedman e Alm, 2012), e più di due terzi dei taxa abbondanti e differenziati dedotti da un test t su un set di dati composizionali di microbiota umani simulati erano spuri(Mandal et al., 2015). Per tenere conto degli effetti composizionali nei set di dati microbici, gli sforzi bioinformatici hanno ri-derivato i metodi statistici comuni, comprese le statistiche di correlazione(Friedman e Alm, 2012; Fang et al., 2015), i test di ipotesi (La Rosa et al., 2012) e la selezione variabile(Chen e Li, 2013; Lin et al., 2014).10.7554/eLife.21887.002Figure 1.PhILR utilizza un albero evolutivo per trasformare i dati dei microbioti in un sistema di coordinate senza vincoli.(A) Due ipotetiche comunità batteriche condividono un numero assoluto identico di Lactobacillus, e di batteri Ruminococcus; si differenziano solo per l’abbondanza assoluta di Bacteroides che è maggiore nella comunità A (cerchio rosso) rispetto alla comunità B (diamante blu).(B) Un diagramma ternario rappresenta i dati proporzionali tipicamente analizzati in un’indagine microbiota basata sul sequenziamento. Si noti che visto in termini di proporzioni lo spazio è limitato e gli assi non sono cartesiani. Di conseguenza, tutti e tre i generi sono cambiati in abbondanza relativa tra le due comunità.(C) Schema della trasformazione PhILR basata su una partizione binaria filogenetica sequenziale. Le coordinate PhILR possono essere viste come “equilibri” tra i pesi (abbondanze relative) dei due sottocladi di un dato nodo interno. Nella comunità B, la maggiore abbondanza di Bacteroides punta l’equilibrio y1* a destra.(D) La trasformazione PhILR può essere vista come un nuovo sistema di coordinate (linee tratteggiate grigie) nello spazio dati proporzionale.(E) I dati trasformati nello spazio PhILR. Si noti che, a differenza dei dati proporzionali grezzi(B), lo spazio PhILR mostra solo una variazione della variabile associata a Bacteroides.DOI:http://dx.doi.org/10.7554/eLife.21887.002
Un approccio alternativo è quello di trasformare i dati microbiota composizionali in uno spazio in cui i metodi statistici esistenti possono essere applicati senza introdurre conclusioni spurie. Questo approccio è interessante per la sua efficienza: la vasta gamma di strumenti dei modelli statistici esistenti può essere applicata senza dover ricorrere a una nuova derivazione. Sono stati proposti metodi di normalizzazione, ad esempio, per modificare i dati di conteggio supponendo che le letture seguano determinate distribuzioni statistiche(ad esempio, il binomio negativo)(Paulson et al., 2013; Anders e Huber, 2010). In alternativa, il campo dell’Analisi dei Dati Composizionali (CoDA) si è concentrato sulla formalizzazione di metodi per trasformare i dati composizionali in una geometria più semplice senza dover assumere che i dati aderiscano a un modello di distribuzione(Bacon-Shone, 2011). Le precedenti analisi dei microbioti hanno già fatto leva sulla teoria del CoDA e hanno utilizzato la trasformazione del rapporto di log centrato per ricostruire le reti e le interazioni delle associazioni microbiche(Kurtz et al., 2015; Lee et al., 2014) e per analizzare le abbondanze differenziali(Fernandes et al., 2014; Gloor et al., 2016b). Tuttavia, la trasformazione del rapporto di log centrato ha un limite cruciale: produce un sistema di coordinate con una matrice di covarianza singolare ed è quindi inadatta a molti modelli statistici comuni(Pawlowsky-Glahn et al., 2015). Questo inconveniente può essere evitato utilizzando un’altra trasformazione CoDA, nota come trasformazione del rapporto isometrico logico (ILR)(Egozcue et al., 2003). La trasformazione ILR può essere costruita a partire da una partizione binaria sequenziale dello spazio variabile originale(Figura 1C), creando un nuovo sistema di coordinate con base ortogonale(Figura 1D ed E)(Egozcue e Pawlowsky-Glahn, 2005). Tuttavia, un ostacolo noto all’utilizzo della trasformazione ILR è la scelta della partizione in modo che le coordinate risultanti siano significative(Pawlowsky-Glahn et al., 2015). Ad oggi, gli studi sui microbioti hanno scelto le coordinate ILR utilizzando partizioni binarie sequenziali ad hoc di gruppi batterici non facilmente interpretabili(Finucane et al., 2014; Lê Cao et al., 2016). In alternativa, sono state utilizzate covariate esterne per selezionare gruppi di taxa batterici da contrastare(Morton et al., 2017).
Qui, introduciamo l’albero filogenetico batterico come una partizione binaria sequenziale naturale e informativa quando si applica la trasformazione ILR a microbiota dataset(Figura 1C). L’utilizzo delle filogenie per costruire la trasformazione ILR si traduce in un sistema di coordinate ILR che cattura le relazioni evolutive tra gruppi batterici vicini (clades). Le analisi dei cladi vicini offrono l’opportunità di una comprensione biologica: le analisi dei cladi hanno collegato la differenziazione genetica all’adattamento ecologico(Hunt et al., 2008) e i livelli relativi dei generi batterici fratelli differenziano le coorti umane in base alla dieta, alla geografia e alla cultura(De Filippo et al., 2010; Wu et al., 2011; Yatsunenko et al., 2012). I set di dati analizzati da una trasformazione ILR filogeneticamente consapevole potrebbero quindi rivelare fattori ecologici ed evolutivi che danno forma alle comunità microbiche associate all’ospite.
Chiamiamo il nostro approccio la trasformazione ILR filogenetica(PhILR). Usando come parametri di riferimento i set di dati ambientali e umani 16S rRNA associati all’uomo, abbiamo scoperto che le semplici distanze euclidee calcolate sui dati della trasformazione PhILR forniscono un’alternativa compositivamente robusta alle misure di distanza/dissimilarità come Bray-Curtis, Jaccard e Unifrac. Inoltre, abbiamo osservato che l’accuratezza dei metodi di classificazione supervisionati sui nostri set di dati di riferimento è stata abbinata o migliorata con i dati trasformati PhILR rispetto all’applicazione degli stessi modelli su dati di abbondanza relativa non trasformati (grezzi) o trasformati in log. La scomposizione delle distanze tra i campioni lungo le coordinate PhILR ha identificato le placche batteriche che possono essersi differenziate per adattarsi a siti corporei distinti. Una decomposizione simile della varianza lungo le coordinate PhILR ha mostrato che, in tutti i siti del corpo umano studiati, il grado di covaria delle placche batteriche vicine tende ad aumentare con la correlazione filogenetica tra le placche. Insieme, questi risultati dimostrano che la trasformazione PhILR può essere utilizzata per migliorare le condotte esistenti di analisi dei microbioti, oltre a consentire nuove analisi filogenetiche degli ecosistemi microbici.
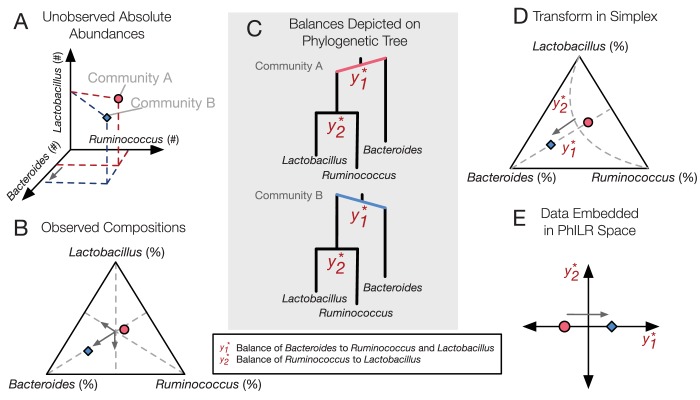
Figura 1.PhILR utilizza un albero evolutivo per trasformare i dati dei microbiota in un sistema di coordinate senza vincoli.(A) Due ipotetiche comunità batteriche condividono lo stesso numero assoluto di Lactobacillus, e di batteri Ruminococcus; si differenziano solo per l’abbondanza assoluta di Bacteroides che è più alta nella comunità A (cerchio rosso) rispetto alla comunità B (diamante blu).(B) Un diagramma ternario rappresenta i dati proporzionali tipicamente analizzati in un’indagine microbiota basata sul sequenziamento. Si noti che visto in termini di proporzioni lo spazio è limitato e gli assi non sono cartesiani. Di conseguenza, tutti e tre i generi sono cambiati in abbondanza relativa tra le due comunità.(C) Schema della trasformazione PhILR basata su una partizione binaria filogenetica sequenziale. Le coordinate PhILR possono essere viste come “equilibri” tra i pesi (abbondanze relative) dei due sottocladi di un dato nodo interno. Nella comunità B, la maggiore abbondanza di Bacteroides punta l’equilibrio y1* a destra.(D) La trasformazione PhILR può essere vista come un nuovo sistema di coordinate (linee tratteggiate grigie) nello spazio dati proporzionale.(E) I dati trasformati nello spazio PhILR. Si noti che, a differenza dei dati proporzionali grezzi(B), lo spazio PhILR mostra solo una variazione della variabile associata a Bacteroides.DOI:
http://dx.doi.org/10.7554/eLife.21887.002
Risultati
Costruire la trasformazione PhILR
La trasformazione PhILR ha due obiettivi. Il primo obiettivo è quello di trasformare i dati microbiota in ingresso in uno spazio non vincolato con una base ortogonale, conservando tutte le informazioni contenute nella composizione originale. Il secondo obiettivo è quello di condurre questa trasformazione utilizzando le informazioni filogenetiche. Per raggiungere questi due obiettivi su un dato set di N campioni costituiti da misure relative di D taxa(Figura 1B), trasformiamo i dati in un nuovo spazio di N campioni e (D-1) coordinate denominate ‘bilance’ (Figura 1C-E) (Egozcue et al.,2003; Egozcue e Pawlowsky-Glahn , 2005). Ogni bilancia yi* è associata ad un singolo nodo interno i di un albero filogenetico con il taxa D come foglie (l’asterisco indica una quantità rappresentata nello spazio PhILR). Il bilancio rappresenta il log-ratio dell’abbondanza relativa media geometrica dei due cladi di taxa che discendono da i (Materiali e metodi). Anche se le singole bilance possono condividere insiemi di foglie sovrapposti e quindi mostrare un comportamento dipendente, l’ILR trasforma le bilance e combina le foglie per formare un sistema di coordinate i cui vettori di base sono ortogonali e le coordinate corrispondenti sono cartesiane(Egozcue et al., 2003; Egozcue e Pawlowsky-Glahn, 2005). L’ortogonalità dei vettori di base permette di utilizzare gli strumenti statistici convenzionali senza artefatti compositivi. La lunghezza unitaria dei vettori di base rende statisticamente comparabili gli equilibri sull’albero anche quando hanno un numero diverso di punte discendenti o esistono a diverse profondità nell’albero(Pawlowsky-Glahn et al., 2015). Inoltre, la lunghezza unitaria assicura che la varianza delle bilance PhILR abbia una scala coerente, a differenza della varianza dei rapporti dei tronchi proposta originariamente da Aitchison(Aitchison, 1986) come misura di associazione, in cui può non essere chiaro cosa costituisca una grande o piccola varianza(Friedman e Alm, 2012).
Mentre la descrizione di cui sopra rappresenta il nucleo della trasformata PhILR, abbiamo anche dotato la trasformata PhILR di due serie di pesi che possono: (1) affrontare la moltitudine di conteggi di zero e quasi zero presenti nei dati dei microbioti; e, (2) incorporare le lunghezze dei rami filogenetici nello spazio trasformato. Poiché i conteggi a zero causano problemi quando si calcolano i log o si esegue la divisione, gli zeri sono spesso sostituiti nelle analisi dei microbiota con piccoli conteggi non a zero. Tuttavia, per evitare la sostituzione degli zeri in eccesso che può di per sé introdurre distorsioni, vengono spesso utilizzate soglie di filtraggio rigide(ad esempio, rimuovendo tutti i taxa che non si vedono con almeno un numero minimo di conteggi in un sottoinsieme di campioni). Tuttavia, le soglie di filtraggio rigido possono rimuovere una frazione sostanziale dei taxa osservati e non tengono conto della bassa precisione (o dell’alta variabilità) dei conteggi vicini allo zero (Glooret al., 2016a; Good, 1956; McMurdie e Holmes, 2014). Abbiamo quindi sviluppato uno schema di “ponderazione dei taxa” che agisce come una sorta di “soft-thresholding”, integrando i metodi di sostituzione dello zero con una forma generalizzata della trasformazione ILR che permette di applicare i pesi ai singoli taxa (Egozcuee Pawlowsky-Glahn, 2016). I pesi sono scelti con un euristico progettato per ridurre l’influenza dei taxa con molti conteggi a zero o quasi zero (Materiali e metodi).
Il nostro secondo schema di ponderazione è chiamato ponderazione della lunghezza del ramo. Alcune analisi possono trarre beneficio dall’incorporazione di informazioni sulle distanze evolutive tra i taxa(Lozupone e Knight, 2005; Fukuyama et al., 2012; Purdom, 2011). Ad esempio, poiché i batteri correlati possono avere più probabilità di condividere tratti simili(Martiny et al., 2015), può essere auspicabile considerare le comunità che si differenziano solo per l’abbondanza di microbi strettamente correlati come più simili rispetto alle comunità che si differenziano solo per l’abbondanza di microbi correlati alla distanza. A causa della corrispondenza uno-a-uno tra gli equilibri PhILR e i nodi interni dell’albero filogenetico, le informazioni evolutive possono essere incorporate nella trasformazione PhILR trasformando gli equilibri filogenetici utilizzando la distanza filogenetica tra i loro discendenti diretti (Materiali e metodi). Notiamo che utilizziamo sia la ponderazione della lunghezza del ramo che la ponderazione del taxon in tutte le nostre analisi successive, tranne dove indicato; tuttavia, questi pesi devono essere considerati come aggiunte facoltative alla trasformazione PhILR del nucleo.
Benchmarking delle analisi a livello di comunità nel sistema di coordinate PhILR
Per illustrare come la trasformazione PhILR può essere utilizzata per eseguire analisi standard a livello di comunità di insiemi di dati microbiota, abbiamo prima esaminato le misure di dissimiglianza della comunità. Le analisi dei microbiota calcolano comunemente la dissimilarità o la distanza tra coppie di campioni e utilizzano queste distanze calcolate a coppie come input per una varietà di strumenti statistici. Abbiamo studiato come le distanze euclidee calcolate su PhILR trasformano i dati rispetto alle comuni misure ecologiche della distanza o della dissimilarità dei microbioti (UniFrac, Bray-Curtis e Jaccard), così come la distanza euclidea applicata ai dati grezzi di abbondanza relativa nelle analisi standard basate sulla distanza. Abbiamo scelto tre diverse indagini sui microbiota come set di dati di riferimento: Costello Skin Sites (CSS), un set di dati di 357 campioni da 12 siti di pelle umana(Costello et al., 2009; Knights et al., 2011); Human Microbiome Project (HMP), un set di dati di 4743 campioni da 18 siti del corpo umano (ades, pelle, vaginale, orale e feci)(Human Microbiome Project Consortium, 2012); e, Global Patterns (GP), un dataset di 26 campioni da nove siti umani o ambientali(Caporaso et al., 2011)(File supplementare 1 e Figura 2-figuresupplement 1).
Le analisi basate sulla distanza, che utilizzano le distanze euclidee calcolate su dati trasformati da PhILR, hanno mostrato prestazioni che rivaleggiano con le comuni misure di distanza ecologica o di difformità. Le principali analisi delle coordinate (PCoA) hanno dimostrato qualitativamente la separazione dei siti corporei utilizzando sia distanze euclidee su dati trasformati in PhILR(Figura 2A) sia con diverse misure di distanza standard calcolate su dati grezzi di abbondanza relativa(Figura 2-figure supplement 2). Per confrontare quantitativamente le misure di distanza, abbiamo testato in che modo le informazioni sull’habitat spiegano la variabilità tra le matrici di distanza misurata dalla statistica R2 di PERMANOVA(Chen et al., 2012). Con questa metrica, la distanza euclidea nel sistema di coordinate PhILR ha superato significativamente le cinque metriche di distanza concorrenti in tutti i casi tranne uno (rispetto a Weighted UniFrac quando applicato al set di dati HMP; Figura 2B).10.7554/eLife.21887.003Figure 2.Performance dei modelli statistici standard sui dati microbiota trasformati PhILR.I benchmark sono stati eseguiti utilizzando tre set di dati: Costello Skin Sites (CSS), Global Patterns (GP), Human Microbiome Project (HMP) (un riassunto di questi dataset dopo la pre-elaborazione è mostrato nel file supplementare 1 e nella Figura 2-figure supplement 1).(A) Distanza campione visualizzata utilizzando l’analisi delle coordinate principali (PCoA) delle distanze euclidee calcolate nel sistema di coordinate PhILR. Un confronto con le PCoA calcolate con altre misure di distanza è mostrato nella Figura 2-figure supplement 2.(B) La distanza del campione (o la difformità) è stata calcolata da una serie di statistiche. I valori di PERMANOVA R2, che rappresentano quanto bene l’identità del campione spiegava la variabilità delle distanze a coppie del campione, sono stati utilizzati come metrica delle prestazioni. Le distanze nello spazio trasformato PhILR sono state calcolate utilizzando la distanza euclidea. Le distanze tra i campioni sui dati grezzi di abbondanza relativa sono state calcolate utilizzando UniFrac pesato e non pesato (WUnifrac e Unifrac, rispettivamente), Bray-Curtis, Binary Jaccard e distanza euclidea. Le barre di errore rappresentano misure di errore standard da 100 repliche di bootstrap e (*) denota un valore p di ≤0,01 dopo la correzione FDR dei test a coppie contro PhILR.(C) Accuratezza dei metodi di classificazione supervisionati testati su set di dati di riferimento. Le barre di errore rappresentano misure standard di errore da 10 test/divisioni del treno e (*) denota un valore p di ≤0,01 dopo la correzione FDR di tutti i test a coppie.DOI:http://dx.doi.org/10.7554/eLife.21887.00310.7554/eLife.21887.004Figuredati a 2 fonti 1.Dati fonte per la Figura 2b e c così come i valori p corretti FDR dei test.DOI:http://dx.doi.org/10.7554/eLife.21887.00410.7554/eLife.21887.005Figuresupplemento a 2 cifre 1.Lo schema di ponderazione dei taxa tende ad assegnare pesi più piccoli ai taxa con più conteggi zero e quasi zero. Il peso di un dato taxon è calcolato come la media geometrica dei suoi conteggi su tutti i campioni per volte la norma euclidea della sua abbondanza relativa su tutti i campioni nel set di dati (Materiali e metodi). I dati sono tracciati su una scala di registro con uno pseudoconteggio di 1 aggiunto per facilitare la visualizzazione.DOI:http://dx.doi.org/10.7554/eLife.21887.00510.7554/eLife.21887.006FigureSupplemento a 2 cifre 2.Principali analisi delle coordinate utilizzando diverse misure di distanza comunitaria o di difformità.DOI:http://dx.doi.org/10.7554/eLife.21887.006
Successivamente, abbiamo testato le prestazioni dei modelli statistici predittivi nel sistema di coordinate PhILR. Abbiamo esaminato quattro tecniche di classificazione standard supervisionate: regressione logistica (LR), macchine vettoriali di supporto (SVM), vicini di k-nearest (kNN) e foreste casuali (RF)(Knights et al., 2011). Abbiamo applicato questi metodi agli stessi tre set di dati di riferimento utilizzati per il confronto delle metriche di distanza. Come linea di base, i metodi di apprendimento automatico sono stati applicati agli insiemi di dati sull’abbondanza relativa grezza e ai dati sull’abbondanza relativa grezza che erano stati trasformati in tronchi.
La trasformazione PhILR ha migliorato significativamente l’accuratezza della classificazione supervisionata in 7 dei 12 compiti di riferimento rispetto alle abbondanze relative grezze(Figura 2C). L’accuratezza è migliorata di oltre il 90% in due benchmark (SVM su HMP e GP), rispetto ai risultati sui dati grezzi. Anche la trasformazione dei log dei dati ha migliorato significativamente l’accuratezza del classificatore su 6 dei 12 parametri di riferimento, ma anche significativamente sottoperformato su un parametro di riferimento rispetto alle abbondanze relative grezze. Inoltre, la trasformazione del PhILR ha migliorato significativamente l’accuratezza della classificazione in 5 dei 12 parametri di riferimento rispetto alla trasformazione del log. Nel complesso, la trasformazione PhILR ha spesso superato le abbondanze relative grezze e le abbondanze relative trasformate in tronchi rispetto all’accuratezza della classificazione e non è mai stata significativamente peggiore.
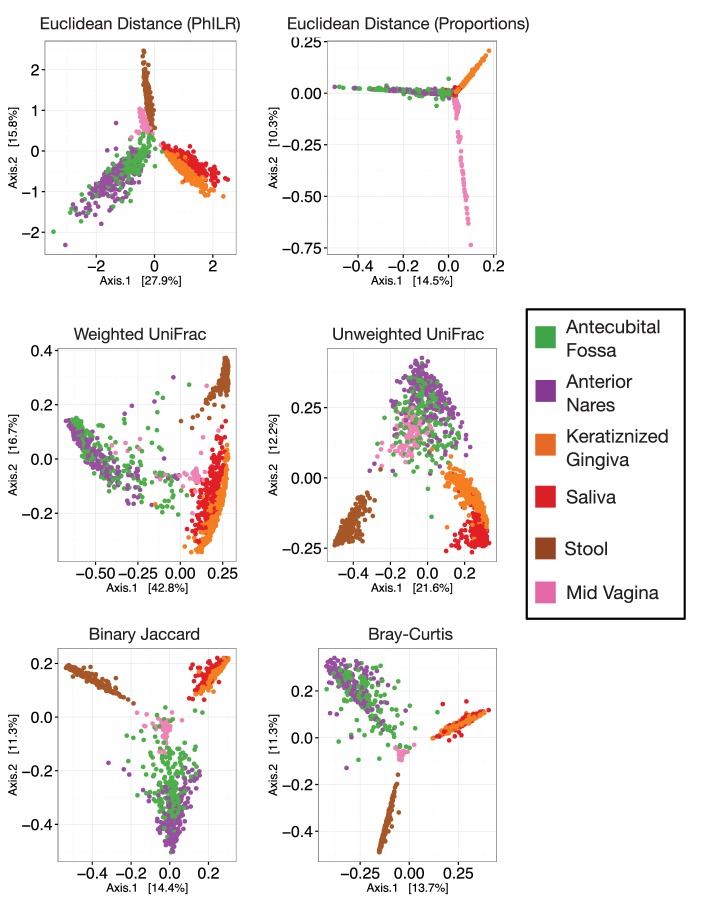
Figura 2-figure supplement 2.Le prestazioni dei modelli statistici standard sui dati dei microbioti trasformati PhILR.dati di partenza per le Figure 2b e c e i valori p corretti FDR dai test.dati di partenza per le Figure 2b e c e i valori p corretti FDR dai test.lo schema di ponderazione dei taxa tende ad assegnare pesi più piccoli ai taxa con più conteggi zero e quasi zero.analisi delle coordinate principali utilizzando diverse misure di distanza comunitaria o di difformità.I benchmark sono stati eseguiti utilizzando tre set di dati: Costello Skin Sites (CSS), Global Patterns (GP), Human Microbiome Project (HMP) (un riassunto di questi dataset dopo la pre-elaborazione è mostrato nel file supplementare 1 e nella figura 2-figure supplement 1).(A) Distanza campione visualizzata utilizzando l’analisi delle coordinate principali (PCoA) delle distanze euclidee calcolate nel sistema di coordinate PhILR. Un confronto con le PCoA calcolate con altre misure di distanza è mostrato nella Figura 2-figure supplement 2.(B) La distanza del campione (o la difformità) è stata calcolata da una serie di statistiche. I valori di PERMANOVA R2, che rappresentano quanto bene l’identità del campione spiegava la variabilità delle distanze a coppie del campione, sono stati utilizzati come metrica delle prestazioni. Le distanze nello spazio trasformato PhILR sono state calcolate utilizzando la distanza euclidea. Le distanze tra i campioni sui dati grezzi di abbondanza relativa sono state calcolate utilizzando UniFrac pesato e non pesato (WUnifrac e Unifrac, rispettivamente), Bray-Curtis, Binary Jaccard e distanza euclidea. Le barre di errore rappresentano misure di errore standard da 100 repliche di bootstrap e (*) denota un valore p di ≤0,01 dopo la correzione FDR dei test a coppie contro PhILR.(C) Accuratezza dei metodi di classificazione supervisionati testati su set di dati di riferimento. Le barre di errore rappresentano misure standard di errore da 10 test/divisioni del treno e (*) denota un valore p di ≤0,01 dopo la correzione FDR di tutti i test a coppie.DOI:
http://dx.doi.org/10.7554/eLife.21887.00310.7554/eLife.21887.004Cifra dati a 2 fonti 1.Dati fonte per la Figura 2b e c così come i valori p corretti FDR dai test.DOI:http://dx.doi.org/10.7554/eLife.21887.004DOI:
http://dx.doi.org/10.7554/eLife.21887.004DOI:
http://dx.doi.org/10.7554/eLife.21887.004Il peso di un dato taxon è calcolato come la media geometrica dei suoi conteggi su tutti i campioni per la norma euclidea della sua abbondanza relativa su tutti i campioni del dataset (Materiali e metodi). I dati sono tracciati su una scala di registro con uno pseudoconteggio di 1 aggiunto per facilitare la visualizzazione.DOI:
http://dx.doi.org/10.7554/eLife.21887.005DOI:
http://dx.doi.org/10.7554/eLife.21887.006

Figura 2-figure supplement 1.Lo schema di ponderazione dei taxa tende ad assegnare pesi più piccoli ai taxa con più conteggi zero e quasi zero.Il peso di un dato taxon è calcolato come la media geometrica dei suoi conteggi su tutti i campioni per volte la norma euclidea della sua abbondanza relativa su tutti i campioni nel set di dati (Materiali e metodi). I dati sono tracciati su una scala di registro con uno pseudoconteggio di 1 aggiunto per facilitare la visualizzazione.DOI:
http://dx.doi.org/10.7554/eLife.21887.005

Figura 2-figure supplement 2.Principali analisi delle coordinate utilizzando diverse misure della distanza della comunità o della dissimiglianza.DOI:
http://dx.doi.org/10.7554/eLife.21887.006
Identificare i clades vicini che differiscono per la preferenza del sito del corpo
Mentre i nostri esperimenti di benchmarking hanno dimostrato come il PhILR ha trasformato i dati ottenuti nelle analisi a livello di comunità, abbiamo anche voluto esplorare le potenziali intuizioni biologiche offerte dal sistema di coordinate PhILR. Abbiamo quindi indagato come le distanze si sono decomposte lungo i bilanci PhILR utilizzando un modello di regressione logistica rado per esaminare quali bilanci distinguono i microbioti del sito del corpo umano nel set di dati HMP. Tali bilance potrebbero essere utilizzate per identificare le placche batteriche vicine le cui abbondanze relative catturano le differenze a livello di comunità tra i microbioti del sito del corpo umano. La differenziazione genetica microbica può essere associata alla specializzazione a nuove risorse o preferenze di stile di vita(Hunt et al., 2008), il che significa che gli equilibri di distinzione vicino alle punte dell’albero batterico possono corrispondere a clade che si adattano agli ambienti del sito del corpo umano.
Abbiamo identificato decine di equilibri altamente discriminatori, che sono stati distribuiti nella filogenesi batterica(Figura 3A e Figura 3-figure supplement 1). Alcuni equilibri discriminatori sono stati trovati in profondità nell’albero. Le abbondanze di Firmicutes, Batteroidetes e Proteobacteria rispetto agli Actinobacteria, Fusobacteria e membri di altri phyla, hanno separato i siti del corpo della pelle dai siti orali e feci(Figura 3B). I livelli del genere Bacteroides relativi al genere Prevotella differenziano i microbioti delle feci da altre comunità del corpo(Figura 3C). In particolare, i valori di equilibri selezionati al di sotto del livello del genere variano anche in base al sito del corpo. I livelli relativi delle specie sorelle di Corynebacterium hanno separato i siti della pelle umana dai siti gengivali(Figura 3D). I livelli di specie a livello di specie bilanciano anche siti differenziati in habitat vicini; i livelli delle specie sorelle di Streptococco o delle specie sorelle di Actinomyces variano a seconda dei siti orali specifici(Figura 3E e F). Questi risultati mostrano che la decomposizione delle distanze tra gruppi di campioni lungo gli equilibri PhILR può essere utilizzata per evidenziare gli equilibri ancestrali che distinguono i microbioti dei siti corporei, così come per identificare equilibri più recenti che possono separare specie che si sono adattate ad abitare siti corporei diversi.10.7554/eLife.21887.007Cifra 3.Equilibri che distinguono i microbioti umani in base al sito corporeo.La regressione logistica ridotta è stata utilizzata per identificare gli equilibri che meglio separano i diversi siti di campionamento (l’elenco completo degli equilibri è fornito nella Figura 3-figure supplement 1).(A) Ogni bilancia è rappresentata sull’albero come una barra grigia rotta. La porzione sinistra della barra identifica il clade nel denominatore del log-ratio, e la porzione destra identifica il clade nel numeratore del log-ratio. Il ramo che porta dai Firmicutes ai Bacteroidetes è stato ridimensionato per facilitare la visualizzazione.(B-F) La distribuzione dei valori di equilibrio tra i siti del corpo. Le linee verticali indicano i valori mediani, le caselle rappresentano gli intervalli interquartile (IQR) e i baffi si estendono a 1,5 IQR su entrambi i lati della mediana. Equilibri tra:(B) i phyla Actinobacteria e Fusobacteria contro i phyla Bacteroidetes, Firmicutes e Proteobacteria distinguono le feci e i siti orali dai siti cutanei;(C) Prevotella s pp. e Bacteroides spp. distinguono le feci dai siti orali; (D) Corynebacterium spp. distinguono i siti cutanei e orali; (E) Streptococcus spp. distinguono i siti orali; (F) Actinomyces spp. distinguono le placche orali dagli altri siti orali. (†) Comprende i Batteroideti, i Firmicuti, gli Alfa, i Beta e i Gamma-proteobatteri. (‡) Include Actinobatteri, Fusobatteri, Epsilon-proteobatteri, Spirochete e Verrucomicrobia.DOI:http://dx.doi.org/10.7554/eLife.21887.00710.7554/eLife.21887.008FigureSupplemento a 3 cifre 1.Saldi trovati per distinguere i siti del corpo umano da una regressione logistica rada.Taxa sono elencati in formato numeratore/denominatore dei saldi.DOI:http://dx.doi.org/10.7554/eLife.21887.008

Figura 3-figure supplement 1.Equilibri che distinguono i microbioti umani in base al sito del corpo. equilibri trovati per distinguere i siti del corpo umano da una regressione logistica rada.La regressione logistica rada è stata utilizzata per identificare gli equilibri che meglio separano i diversi siti di campionamento (l’elenco completo degli equilibri è fornito nella Figura 3-figure supplement 1).(A) Ogni bilancia è rappresentata sull’albero come una barra grigia rotta. La porzione sinistra della barra identifica il clade nel denominatore del log-ratio, e la porzione destra identifica il clade nel numeratore del log-ratio. Il ramo che porta dai Firmicutes ai Bacteroidetes è stato ridimensionato per facilitare la visualizzazione.(B-F) La distribuzione dei valori di equilibrio tra i siti del corpo. Le linee verticali indicano i valori mediani, le caselle rappresentano gli intervalli interquartile (IQR) e i baffi si estendono a 1,5 IQR su entrambi i lati della mediana. Equilibri tra:(B) i phyla Actinobacteria e Fusobacteria contro i phyla Bacteroidetes, Firmicutes e Proteobacteria distinguono le feci e i siti orali dai siti cutanei;(C) Prevotella s pp. e Bacteroides spp. distinguono le feci dai siti orali; (D) Corynebacterium spp. distinguono i siti cutanei e orali; (E) Streptococcus spp. distinguono i siti orali; (F) Actinomyces spp. distinguono le placche orali dagli altri siti orali. (†) Comprende i Batteroideti, i Firmicuti, gli Alfa, i Beta e i Gamma-proteobatteri. (‡) Include Actinobatteri, Fusobatteri, Epsilon-proteobatteri, Spirochete e Verrucomicrobia.DOI:
http://dx.doi.org/10.7554/eLife.21887.007I taxa sono elencati in formato numeratore/denominatore di bilancio.DOI:
http://dx.doi.org/10.7554/eLife.21887.008

Figura 3-figure supplement 1.Bilanci trovati per distinguere i siti del corpo umano da una regressione logistica rada.I taxa sono elencati in formato numeratore/denominatore di equilibri.DOI:
http://dx.doi.org/10.7554/eLife.21887.008
Varianza di equilibrio e montaggio dei microbioti
Come naturale estensione della nostra analisi di come la distanza si decompone lungo le bilance PhILR, abbiamo poi indagato come la varianza delle bilance si decompone nel sistema di coordinate PhILR. La varianza dell’equilibrio è una misura dell’associazione tra le placche batteriche vicine. Quando la varianza di un equilibrio tra due clade si avvicina a zero, l’abbondanza media di taxa in ciascuna delle due clade sarà linearmente correlata e quindi covaria attraverso gli habitat microbici(Lovell et al., 2015). Al contrario, quando un equilibrio presenta un’elevata varianza, le clade batteriche correlate presentano modelli non collegati o escludenti tra i campioni. A differenza delle misure standard di associazione(ad esempio, la correlazione Pearson), la varianza dell’equilibrio è robusta rispetto agli effetti compositivi(Pawlowsky-Glahn et al., 2015).
La nostra indagine preliminare ha dimostrato un modello sorprendente in cui la varianza di equilibrio è diminuita per gli equilibri più vicini alle punte della filogenesi ed è aumentata per gli equilibri più vicini alla radice. Per determinare se questo modello osservato non fosse il risultato di un artefatto tecnico, abbiamo fatto i seguenti tre passi. In primo luogo, abbiamo omesso i pesi della lunghezza dei rami dalla trasformazione, in quanto abbiamo anticipato che la lunghezza dei rami può variare in modo non casuale in funzione della profondità nella filogenesi. In secondo luogo, abbiamo anticipato che gli equilibri vicino alle punte della filogenesi sarebbero stati associati a un minor numero di conteggi di lettura e quindi sarebbero stati più influenzati dalla nostra euristica scelta per la ponderazione del taxon e la sostituzione zero. Abbiamo quindi omesso la ponderazione del taxon, abbiamo impiegato soglie di filtraggio più rigorose e condizionato il nostro calcolo della varianza delle bilance sui conteggi non zero piuttosto che utilizzare la sostituzione zero (Materiali e metodi). In terzo luogo, abbiamo combinato la regressione e uno schema di permutazione per testare l’ipotesi nulla che il grado di covaria dei clades vicini sia indipendente dalla distanza filogenetica tra loro (Materiali e metodi). Permutando le etichette delle punte sull’albero, il nostro test genera un sottoinsieme ristretto di partizioni binarie sequenziali casuali che mantiene ancora la variabilità di conteggio (e potenziali distorsioni dovute ai nostri metodi di manipolazione zero) dei dati osservati.
Con la nostra analisi PhILR modificata, abbiamo osservato una significativa diminuzione delle variazioni di equilibrio vicino alle punte dell’albero filogenetico per tutti i siti del corpo nel set di dati HMP (p<0,01, test di permutazione con correzione FDR; Figura 4A-F e Figura 4-figure supplements 1- 2). In prossimità delle foglie dell’albero predominano i bilanci a bassa varianza. Esempi di tali equilibri hanno coinvolto specie di B. fragilis nelle feci(Figura 4H), specie di Rothia mucilaginosa nella mucosa buccale(Figura 4J), e specie di Lactobacillus nella media vagina(Figura 4L). Al contrario, gli equilibri di varianza più elevati tendevano ad essere più basali sull’albero. Tre esempi di equilibri di varianza elevati corrispondono a livelli di clade nell’ordine(Figura 4G), famiglia(Figura 4I) e genere (Figura4K). Abbiamo anche osservato che la relazione tra la varianza dell’equilibrio e la profondità filogenetica variava a diverse scale tassonomiche. La regressione LOESS ha rivelato che le tendenze tra la varianza e la profondità filogenetica erano più forti al di sopra del livello della specie che al di sotto di esso (Materiali e metodi; Figura 4D-F e figura 4-figure supplement 2). Nel complesso, il modello osservato di variazione decrescente dell’equilibrio vicino alle punte dell’albero filogenetico ha suggerito che i batteri strettamente correlati tendono a covarsi nei siti del corpo umano.10.7554/eLife.21887.009Figure 4.Neighbighboring clades covary meno con l’aumento della profondità filogenetica.La varianza dei valori di equilibrio cattura il grado in cui i clades vicini covano, con variazioni di equilibrio più piccole che rappresentano clades sorella che covano più fortemente(Figura 4-figure supplement 1).(A-C) Le variazioni di equilibrio sono state calcolate tra i campioni di feci (A), mucosa buccale (B), e la metà della vagina (C). I rami rossi indicano una piccola variazione di equilibrio e i rami blu indicano una variazione di equilibrio elevata. Gli equilibri 1-6 sono tracciati individualmente in pannelli (D-L).(D-F) Le variazioni di equilibrio all’interno di ogni sito corporeo aumentano linearmente con l’aumento della profondità filogenetica su una scala log (linea blu; p<0,01, test di permutazione con correzione FDR; Metodi ). Tendenze significative si osservano in tutti gli altri siti del corpo(Figura 4-figure supplementi 2 e 3). La regressione non parametrica LOESS (linea verde e corrispondente intervallo di confidenza del 95%) rivela un punto di inflessione nella relazione tra la profondità filogenetica e la varianza dell’equilibrio. Questo punto di inflessione appare al di sotto del livello di specie stimato (‘s’ linea tratteggiata; la profondità mediana oltre la quale gli equilibri non implicano più la condivisione della stessa assegnazione di specie da parte delle foglie; Materiali e metodi).(G-L) Esempi di equilibri con alta e bassa varianza da pannelli (A-F). Le variazioni basse degli equilibri(H, J, L) riflettono una relazione lineare tra i mezzi geometrici delle abbondanze delle placche sorelle. Variazioni di equilibrio elevate(G, I, K) riflettono dinamiche non collegate o dinamiche di esclusione tra i mezzi geometrici delle abbondanze dei clades sorelle.DOI:http://dx.doi.org/10.7554/eLife.21887.00910.7554/eLife.21887.010Figure4.Codice sorgente 1.Codice sorgente per la figura 4 e i supplementi associati.DOI:http://dx.doi.org/10.7554/eLife.21887.01010.7554/eLife.21887.011Figure4—dati fonte 1.FDR corretti p-valori corretti dai test di permutazione.DOI:http://dx.doi.org/10.7554/eLife.21887.01110.7554/eLife.21887.012FigureSupplemento a 4 cifre 1.Bilanci con varianza alta e bassa. Sono mostrati i 10 bilanci con varianza più alta e i 10 bilanci con varianza più bassa per il sito del corpo delle feci nel set di dati HMP. Pannelli 1-10: Le variazioni di scostamento basse riflettono una relazione lineare (attraverso l’origine) tra i livelli dei due clades che discendono da un dato equilibrio. Pannelli 11-20: Le variazioni degli equilibri elevati mancano di questa relazione lineare.DOI:http://dx.doi.org/10.7554/eLife.21887.01210.7554/eLife.21887.013FigureSupplemento a 4 cifre 2.I clades vicini si covano meno con l’aumento della profondità filogenetica. Le linee tratteggiate indicano i confini delle specie mediane (vedi Materiali e metodi).DOI:http://dx.doi.org/10.7554/eLife.21887.01310.7554/eLife.21887.014Figuresupplemento a 4 cifre 3.La distribuzione nulla per β.β è la pendenza nella regressione lineare tra la varianza dell’equilibrio e la profondità filogenetica nello spazio del tronco (regressioni mostrate in figura supplemento a 4 cifre 2). Per formare distribuzioni nulle per β, le etichette delle punte sulla filogenesi sono state rimescolate (n = 20.000) e i valori di equilibrio sono stati ricalcolati. Le distribuzioni per β sono simmetriche circa 0 per ogni sito del corpo, suggerendo.DOI:http://dx.doi.org/10.7554/eLife.21887.014
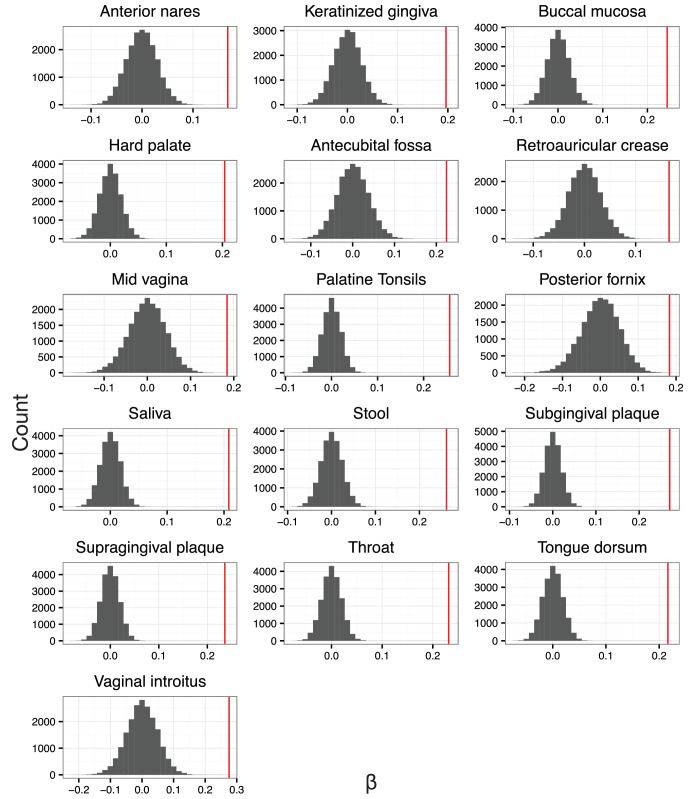
Figura 4-figure supplement 3.Figura 4—integratore figura 3. Clades vicine meno covari con l’aumento della profondità filogenetica.codice sorgente per la figura 4 e relativi integratori.FDR corretto p-valori p da test di permutazione.codice sorgente per la figura 4 e relativi integratori.FDR corretto p-valori p da test di permutazione.saldi con alta e bassa varianza.clades vicine meno covari con l’aumento della profondità filogenetica.la distribuzione nulla per la β.La varianza dei valori di equilibrio cattura il grado di covarianza dei clades vicini, con variazioni di equilibrio più piccole che rappresentano clades fratelli che covariano più fortemente(Figura 4-figure supplement 1).(A-C) Le variazioni di equilibrio sono stati calcolati tra i campioni di feci (A), mucosa buccale (B), e la metà della vagina (C). I rami rossi indicano una piccola variazione di equilibrio e i rami blu indicano una variazione di equilibrio elevata. Gli equilibri 1-6 sono tracciati individualmente in pannelli (D-L).(D-F) Le variazioni di equilibrio all’interno di ogni sito corporeo aumentano linearmente con l’aumento della profondità filogenetica su una scala log (linea blu; p<0,01, test di permutazione con correzione FDR; Metodi ). Tendenze significative si osservano in tutti gli altri siti del corpo(Figura 4-figure supplementi 2 e 3). La regressione non parametrica LOESS (linea verde e corrispondente intervallo di confidenza del 95%) rivela un punto di inflessione nella relazione tra la profondità filogenetica e la varianza dell’equilibrio. Questo punto di inflessione appare al di sotto del livello di specie stimato (‘s’ linea tratteggiata; la profondità mediana oltre la quale gli equilibri non implicano più la condivisione della stessa assegnazione di specie da parte delle foglie; Materiali e metodi).(G-L) Esempi di equilibri con alta e bassa varianza da pannelli (A-F). Le variazioni basse degli equilibri(H, J, L) riflettono una relazione lineare tra i mezzi geometrici delle abbondanze delle placche sorelle. Variazioni di equilibrio elevate(G, I, K) riflettono dinamiche non collegate o dinamiche di esclusione tra i mezzi geometrici delle abbondanze dei clades sorelle.DOI:
http://dx.doi.org/10.7554/eLife.21887.00910.7554/eLife.21887.010Codice sorgente a 4 cifre 1.Codice sorgente per la figura 4 e relativi supplementi.DOI:http://dx.doi.org/10.7554/eLife.21887.010DOI:
http://dx.doi.org/10.7554/eLife.21887.01010.7554/eLife.21887.011Cifra dati a 4 fonti 1.FDR corretti p-valori p da test di permutazione.DOI:http://dx.doi.org/10.7554/eLife.21887.011DOI:
http://dx.doi.org/10.7554/eLife.21887.011DOI:
http://dx.doi.org/10.7554/eLife.21887.010DOI:
http://dx.doi.org/10.7554/eLife.21887.011Sono mostrati i 10 bilanci di varianza più alti e i 10 bilanci di varianza più bassi per il sito del corpo dello sgabello nel set di dati HMP. Pannelli 1-10: Le basse varianze di bilanciamento riflettono una relazione lineare (attraverso l’origine) tra i livelli delle due placche che discendono da un dato bilanciamento. Pannelli 11-20: Le variazioni degli equilibri elevati mancano di questa relazione lineare.DOI:
http://dx.doi.org/10.7554/eLife.21887.012Qui sono mostrati tutti i siti di corpi di HMP. Le linee tratteggiate indicano i confini delle specie mediane (vedi Materiali e metodi).DOI:
http://dx.doi.org/10.7554/eLife.21887.013β è la pendenza nella regressione lineare tra la varianza dell’equilibrio e la profondità filogenetica nello spazio del tronco (regressioni mostrate in Figura 4-figure supplement 2). Per formare distribuzioni nulle per β, le etichette delle punte sulla filogenesi sono state rimescolate (n = 20.000) e i valori di equilibrio sono stati ricalcolati. Le distribuzioni per β sono simmetriche circa 0 per ogni sito del corpo, suggerendo.DOI:
http://dx.doi.org/10.7554/eLife.21887.014
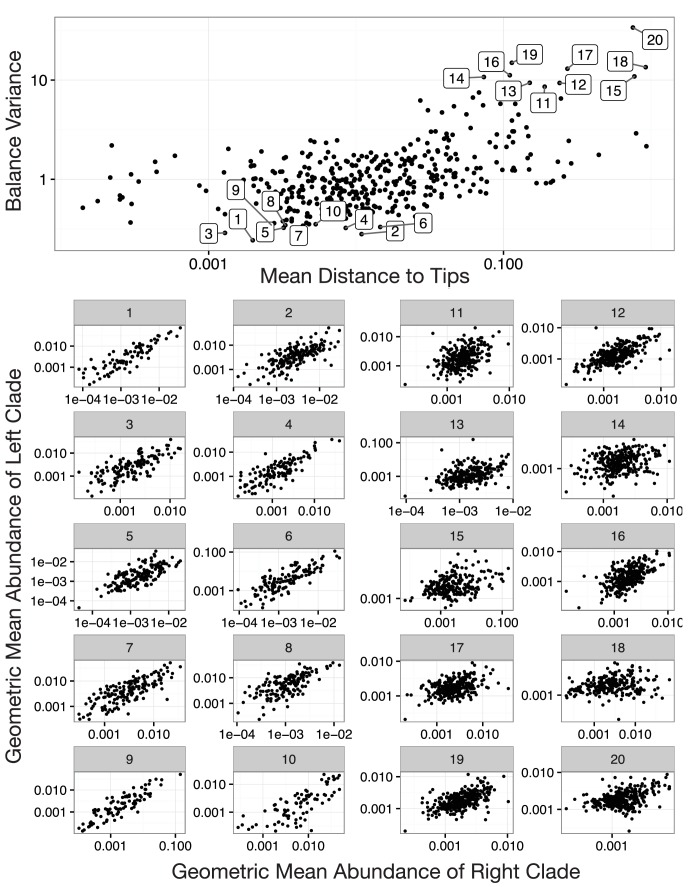
Figura 4-figure supplement 1.Saldi con alta e bassa varianza.Sono mostrati i 10 bilanci con la varianza più alta e i 10 bilanci con la varianza più bassa per il sito del corpo dello sgabello nel set di dati HMP. Pannelli 1-10: Le variazioni di scostamento basse riflettono una relazione lineare (attraverso l’origine) tra i livelli delle due placche che discendono da un dato equilibrio. Pannelli 11-20: Le variazioni degli equilibri elevati mancano di questa relazione lineare.DOI:
http://dx.doi.org/10.7554/eLife.21887.012
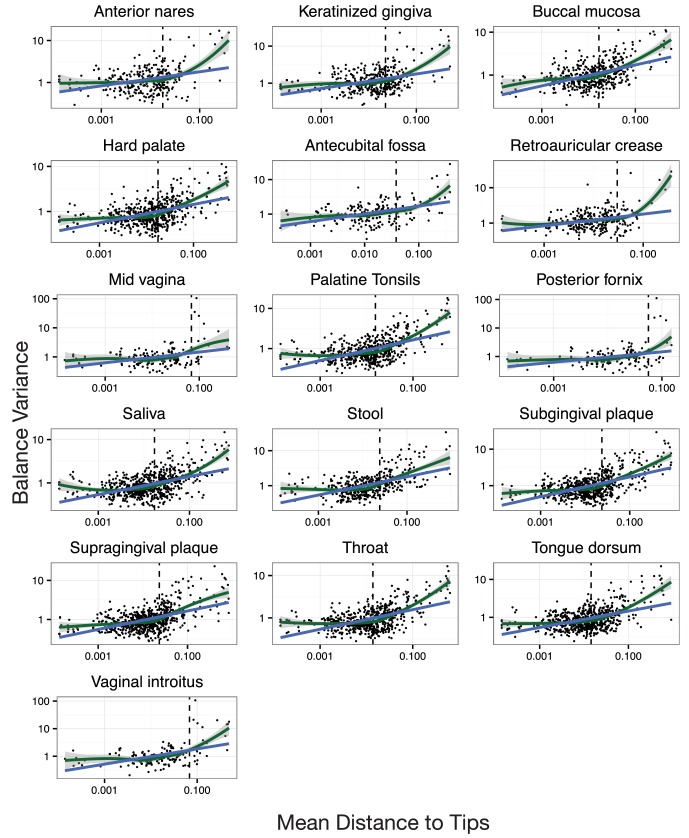
Figura 4-figure supplement 2.I clades vicini si covano meno con l’aumento della profondità filogenetica.Qui sono mostrati tutti i siti del corpo HMP. Le linee tratteggiate indicano i confini delle specie mediane (vedi Materiali e metodi).DOI:
http://dx.doi.org/10.7554/eLife.21887.013

Figura 4-figure supplement 3.La distribuzione nulla per β.β è la pendenza nella regressione lineare tra la varianza dell’equilibrio e la profondità filogenetica nello spazio del tronco (regressioni mostrate in Figura 4-figure supplement 2). Per formare distribuzioni nulle per β, le etichette delle punte sulla filogenesi sono state rimescolate (n = 20.000) e i valori di equilibrio sono stati ricalcolati. Le distribuzioni per β sono simmetriche circa 0 per ogni sito del corpo, suggerendo.DOI:
http://dx.doi.org/10.7554/eLife.21887.014
Discussione
Esiste una simbiosi tra la nostra comprensione dell’evoluzione batterica e l’ecologia delle comunità microbiche associate all’ospite(Matsen, 2015). Studi sui microbi hanno dimostrato che i mammiferi e i batteri si sono specializzati in milioni di anni(Moeller et al., 2016; Ley et al., 2008), e i microbi dell’intestino umano hanno rivelato le forze che guidano il trasferimento orizzontale dei geni tra i batteri(Smillie et al., 2011). Strumenti e teorie evolutive sono stati utilizzati per spiegare come la cooperazione sia vantaggiosa per i membri delle comunità microbiche intestinali(Rakoff-Nahoum et al., 2016), e sollevano la preoccupazione che l’aumento dei tassi di malattie croniche sia legato al disturbo dei microbioti(Blaser e Falkow, 2009). In questo caso, abbiamo cercato di continuare a costruire legami tra l’evoluzione dei microbioti e l’ecologia, progettando una trasformazione dei dati che utilizzi modelli filogenetici per superare le sfide associate ai dati compositivi, consentendo al tempo stesso nuove analisi evolutive.
Abbiamo scoperto che il sistema di coordinate PhILR risultante, almeno per quanto riguarda le metriche di performance scelte, ha portato a un significativo miglioramento delle prestazioni per una varietà di analisi a livello comunitario ora utilizzate nell’analisi dei microbiota. Mentre questi risultati aggiungono credibilità al nostro approccio proposto, sottolineiamo che non riteniamo essenziale che PhILR dimostri prestazioni di riferimento superiori per motivare il suo utilizzo nell’analisi dei microbiota. Riteniamo che la necessità di strumenti compositivamente robusti sia già stata ben stabilita(Jackson, 1997; Friedman e Alm, 2012; Aitchison, 1986; Lovell et al., 2011; Gloor et al., 2016a; Li, 2015; Tsilimigras e Fodor, 2016) e abbiamo voluto che questi benchmark dimostrassero la flessibilità e l’utilità di lavorare con i dati trasformati di PhILR. Notiamo inoltre che per alcune analisi, una trasformazione ILR basata sulla filogenesi non supererà una trasformazione ILR costruita a partire da un’altra partizione binaria sequenziale. Infatti, in assenza di pesi di lunghezza delle diramazioni, qualsiasi partizione ILR casuale produrrebbe risultati equivalenti sui nostri compiti di benchmark. Invece, ciò che distingue la trasformata PhILR dalle altre trasformazioni ILR è l’interpretabilità delle coordinate trasformate. Gli equilibri nello spazio PhILR corrispondono ad eventi di speciazione, che possono essere una fonte per la comprensione biologica.
Ad esempio, l’esecuzione della regressione sui dati trasformati del PhILR ci ha permesso di decomporre la distanza tra le comunità batteriche su singoli punti della filogenesi, evidenziando gli equilibri in prossimità delle punte dell’albero che contraddistinguono i siti del corpo umano. Questi equilibri possono riflettere la specializzazione funzionale, poiché la compartimentazione ecologica tra le placche batteriche recentemente differenziate potrebbe essere causata dall’adattamento genetico a nuovi ambienti o stili di vita(Hunt et al., 2008). Infatti, tra i siti del corpo orale, abbiamo osservato una consistente specificità del sito di clade batteriche vicine all’interno dei generi Actinomyces(Figura 3F) e Streptococcus(Figura 3E). In precedenza sono state osservate specie all’interno dei generi Actinomyces per la suddivisione per siti orali(Aas et al., 2005; Mager et al., 2003). Ancora più eterogeneità è stata osservata all’interno del genere Streptococcus, dove sono state identificate specie che distinguono denti, placca, mucosa, lingua, saliva e altre sedi orali(Aas et al., 2005; Mager et al., 2003). Questa suddivisione riflette probabilmente la variazione dell’anatomia e della disponibilità di risorse tra le regioni della bocca(Aas et al., 2005), così come i tipi di superfici a cui possono aderire i ceppi batterici(Mager et al., 2003).
Abbiamo anche osservato prove di potenziale adattamento all’interno del gene a siti corporei che non sono state precedentemente segnalate. All’interno del genere Corynebacterium, abbiamo trovato rapporti di taxa variabili tra placche orali e siti cutanei selezionati(Figura 3D). Sebbene il genere sia ora apprezzato per favorire gli ambienti cutanei umidi, il ruolo svolto dai singoli Corynebatteri all’interno dei microbioti cutanei rimane incompleto(Grice e Segre, 2011). Il collegamento preciso di singole specie di Corynebacterium o ceppi di Corynebacterium ai siti del corpo è al di là dell’ambito di questo studio a causa della limitata risoluzione tassonomica dei set di dati 16S rRNA(Janda e Abbott, 2007; Větrovský e Baldrian, 2013). Tuttavia, riteniamo che il sistema di coordinate PhILR possa essere utilizzato in futuro per identificare gruppi di taxa batterici correlati che hanno subito un recente adattamento funzionale.
Un altro esempio di come la trasformazione PhILR possa fornire intuizioni biologiche è emerso dalla nostra analisi di come la varianza dei microbioti umani si decompone lungo gli equilibri individuali. Abbiamo osservato che gli equilibri tra i taxa più filogeneticamente correlati erano significativamente più probabili di covarsi di quanto ci si aspettasse per caso. Questo modello potrebbe riflettere le forze evolutive ed ecologiche che strutturano le comunità microbiche nel corpo umano. Si è ipotizzato che i taxa batterici correlati abbiano caratteristiche di stile di vita simili(Martiny et al., 2015; Zaneveld et al., 2010), e potrebbero quindi covarsi in siti del corpo umano che favoriscono i loro tratti comuni(Levy e Borenstein, 2013; Faust et al., 2012). Una spiegazione alternativa per i modelli di variazione del bilancio che abbiamo osservato è che gli errori di sequenziamento e gli artefatti di clustering di lettura sono suscettibili di produrre OTU (Unità tassonomiche operative) con sequenze di riferimento e distribuzioni simili tra i campioni. Anche se non possiamo escludere definitivamente questa ipotesi alternativa, notiamo che non spiegherebbe perché il segnale per la co-variazione dei taxa è più debole per gli equilibri a livelli tassonomici più alti e appare a plateau per gli equilibri vicini o inferiori al livello della specie. Una spiegazione biologica per il segnale di plateauing sarebbe che le caratteristiche dello stile di vita che permettono ai batteri di persistere nei siti del corpo umano sono conservate tra i ceppi più o meno corrispondenti alla stessa specie. Sono necessari studi di follow-up per capire in modo più definitivo come i modelli di variazione degli equilibri tra le filogenie possono essere interpretati dal punto di vista evolutivo.
Sebbene i metodi qui presentati forniscano un quadro geometrico coerente per l’esecuzione di analisi dei microbioti libere da artefatti compositivi, sono possibili futuri perfezionamenti. In particolare, si evidenziano le questioni relative alla scelta dei pesi, alla gestione dei valori zero e alla perdita di informazioni durante la normalizzazione del conteggio. Sia i pesi dei taxa che i pesi delle lunghezze dei rami che introduciamo qui possono essere considerati come euristiche preliminari; il lavoro futuro produrrà probabilmente ulteriori schemi di ponderazione, così come la conoscenza di quando un dato schema di ponderazione dovrebbe essere abbinato a un compito di analisi. Nel caso di un apprendimento macchina supervisionato, la selezione dei pesi potrebbe essere ottimizzata come parte del processo di formazione. Inoltre, se è importante che i dati trasformati abbiano coordinate numeriche significative, in modo tale che si desideri interpretare l’esatto valore numerico di una data bilancia in un campione, suggeriamo di non utilizzare né pesi di lunghezza del ramo né pesi di taxa, poiché questi pesi possono complicare questo tipo di interpretazione. Per quanto riguarda la nostra gestione dei valori zero, questa scelta progettuale del modello affronta una sfida eccezionale per l’analisi dei microbiota e dei dati compositivi(Tsilimigras e Fodor, 2016; Martın-Fernandez et al., 2011). Parte della difficoltà di questa sfida è rappresentata dal fatto che un valore zero rappresenti un valore al di sotto del limite di rilevazione (zero arrotondato) o un taxon realmente assente (zero essenziale). In questo caso, impieghiamo la sostituzione zero, il che implica l’ipotesi che tutti i valori zero rappresentino degli zeri arrotondati. Nuovi modelli di miscela che permettono esplicitamente sia gli zeri essenziali che quelli arrotondati(Bear e Billheimer, 2016), così come metodi più avanzati di sostituzione dello zero(Martın-Fernandez et al., 2011; Martin-Fernandez et al., 2015), possono permetterci di gestire gli zeri in modo più sofisticato. Infine, per quanto riguarda la perdita di informazioni causata dalla normalizzazione, è noto che il numero di conteggi misurati per un dato taxon influenza la precisione con cui possiamo stimare la sua abbondanza relativa in un campione(Gloor et al., 2016a; Good, 1956; McMurdie e Holmes, 2014). Mentre i nostri pesi dei taxa sono destinati ad affrontare questa idea, un modello completamente probabilistico dei conteggi fornirebbe probabilmente dei limiti di errore più accurati per l’inferenza. Noi crediamo che sarebbe possibile costruire un tale modello in un quadro bayesiano, osservando i conteggi osservati come tratti multinazionali da un punto dello spazio trasformato dal PhILR, come è stato fatto per altri spazi basati su log-ratio(Billheimer et al., 2001).
Oltre a perfezionare la trasformazione PhILR, lo sforzo futuro può anche essere diretto verso l’interpretazione dei risultati della trasformazione a livello di singolo taxon. Gli studi sui microbiota si concentrano spesso sui singoli taxa per compiti come l’identificazione di specifici batteri che sono causali o biomarcatori di malattia. Gli approcci log-ratio possono fornire un approccio compositivamente robusto per l’identificazione di biomarcatori basati sui cambiamenti nella relativa abbondanza dei singoli taxa. Grazie alla corrispondenza uno-a-uno tra le coordinate CLR e i taxa individuali, la trasformazione CLR è stata utilizzata in precedenza per costruire modelli compositivamente robusti in termini di taxa individuali(Mandal et al., 2015; Kurtz et al., 2015; Fernandes et al., 2014). Tuttavia, i dati trasformati CLR soffrono dell’inconveniente di una matrice di covarianza singolare, che può rendere difficile lo sviluppo di nuovi modelli basati sulla trasformazione CLR(Pawlowsky-Glahn et al., 2015). I dati trasformati ILR non soffrono di questo inconveniente(Pawlowsky-Glahn et al., 2015) e, inoltre, possono essere analizzati a livello di singolo taxon. Per fare ciò, la trasformazione ILR inversa può essere applicata ai risultati del modello generati in un sistema di coordinate ILR, producendo analisi in termini di variazioni dell’abbondanza relativa dei singoli taxa(Pawlowsky-Glahn et al., 2015). L’uso della trasformazione ILR inversa in questo modo è ben stabilito(Pawlowsky-Glahn et al., 2015; van den Boogaart e Tolosana-Delgado, 2013; Pawlowsky-Glahne Buccianti, 2011) e la trasformazione inversa è fornita nei Metodi (Egozcue ePawlowsky-Glahn, 2016).
Nonostante questi percorsi di miglioramento, modifica o estensione, riteniamo che la trasformazione PhILR permetta già oggi di applicare i metodi statistici esistenti ai set di dati metagenomici, liberi da artefatti compositivi e inquadrati secondo una prospettiva evolutiva. Prevediamo che la trasformazione PhILR venga utilizzata come trasformazione predefinita prima di molte analisi di microbiota, soprattutto se si desidera una prospettiva filogenetica. Ad esempio, la trasformazione PhILR potrebbe essere utilizzata al posto della trasformazione convenzionale del log, che spesso è la scelta di default nell’analisi dei microbioti, ma non è robusta rispetto agli effetti compositivi. La sostituzione del PhILR nelle pipeline bioinformatiche esistenti dovrebbe essere spesso senza soluzione di continuità e sottolineiamo che tutti gli strumenti statistici applicati ai dati trasformati PhILR in questo studio sono stati utilizzati “off-the-shelf” e senza modifiche. È importante sottolineare che tale sostituzione contrasta con l’approccio alternativo per la contabilizzazione dei dati sui microbiota composizionali, che consiste nel modificare le tecniche statistiche esistenti. Tale modifica è spesso impegnativa perché molte statistiche sono state derivate assumendo uno spazio non vincolato con una base ortogonale, non uno spazio compositivo vincolato e sovradeterminato. Pertanto, mentre le tecniche selezionate sono già state adattate(ad esempio le misure di distanza che incorporano informazioni filogenetiche(Lozupone e Knight, 2005) e i metodi di selezione che gestiscono l’input compositivo(Chen e Li, 2013; Lin et al., 2014)), è probabile che alcuni obiettivi statistici, come la previsione non lineare della comunità o la modellazione del sistema di controllo, possano rivelarsi troppo complessi per adattarsi alla natura compositiva dei set di dati dei microbiota. Infine, oltre alle indagini sui microbiota, riconosciamo anche che i set di dati metagenomici composizionali sono generati quando si studia l’ecologia delle comunità virali(Culley et al., 2006) o la struttura della popolazione clonale nel cancro(Britanova et al., 2014; Yuan et al., 2015; Roth et al., 2014). Ci aspettiamo che il PhILR si trasformi per aiutare altre aree di ricerca biologica dove le variabili sono misurate dall’abbondanza relativa e collegate da un albero evolutivo.
Materiali e metodi
La trasformazione ILR
Un tipico campione microbico è costituito da conteggi misurati cj per taxa j∈{1, …, D}. Un’operazione standard è quella di prendere i dati di conteggio e trasformarli in abbondanze relative. Questa operazione viene chiamata chiusura nell’analisi dei dati composizionali(Aitchison, 1986) e viene data dax= C[(c1,⋯,cD)]=(c1∑jcj,…,cD∑jcj)
dove x rappresenta un vettore di abbondanze relative per il taxa D nel campione. Possiamo rappresentare un albero filogenetico binario del taxa D utilizzando una matrice di segni Θ introdotta da Pawlowsky-Glahn e Egozcue (Pawlowsky-Glahne Egozcue, 2011) e mostrata nella Figura 5. Ogni riga della matrice dei segni indicizza un nodo interno i dell’albero e ogni colonna indicizza una punta dell’albero. Un dato elemento nella matrice dei segni è ±1 a seconda di quale dei due clade discendenti da i quella punta è una parte di e 0 se quella punta non è una discendente di i. L’assegnazione di +1 contro -1 determina quale clade è rappresentato nel numeratore contro il denominatore del corrispondente log-ratio (come descritto di seguito). Scambiando questa assegnazione con una data bilancia si cambia quale clade è rappresentato nel numeratore contro il denominatore del rapporto log. Seguendo Egozcue e Pawlowsky-Glahn(Egozcue e Pawlowsky-Glahn, 2016), rappresentiamo la coordinata ILR (saldo) associata al nodo i in termini di composizione spostata y=x/p=(x1/p1,…,xD/pD) come(1)yi∗=ni+ni+ni-ni+++ni-loggp(yi+)gp(yi-) .10.7554/eLife.21887.015Figure 5.Sign matrix representation of a phylogenetic tree.A binary tree(Left) può essere rappresentato da una matrice di segni(Right) denota Θ.DOI:http://dx.doi.org/10.7554/eLife.21887.015
Qui, gp(yi+) e gp(yi-) rappresentano la media geometrica ponderata delle componenti di y che rappresentano le punte nel clade +1 o -1 discendente dal nodo i rispettivamente. Questa media geometrica ponderata è data da(2)gp(yi±)=exp(∑(θij=±1)pjlog yj∑(θij=±1)pj)
dove pj è il peso assegnato a taxa j. Il termine ni+ni-/ni++ni+ni- nell’equazione 1 è il termine di scala che assicura che l’elemento base ILR abbia lunghezza unitaria e i termini ni± sono dati da(3)ni±=∑θij=±1pj.
Si noti che quando p=(1,…,1), y=x, Equazione 1 rappresentano la trasformazione ILR come originariamente pubblicata (Egozcue etal., 2003), l’equazione 2 rappresenta la formula standard per la media geometrica di un vettore y, e l ‘equazione 3 rappresenta il numero di punte che discendono dal discendente del clade +1 o -1 del nodo i. Tuttavia, quando p≠(1,…,1), queste tre equazioni rappresentano una forma più generalizzata della trasformazione ILR che permette di assegnare pesi ai taxa nello spazio trasformato (Egozcuee Pawlowsky-Glahn, 2016).
Dopo Egozcue e Pawlowsky-Glahn(Egozcue e Pawlowsky-Glahn, 2016), notiamo anche che la forma della trasformazione ILR generalizzata (che indicheremo ilrp) può essere riscritta in termini di una trasformazione CLR generalizzata (che indicheremo clrp). Questa formulazione in termini di trasformazione CLR generalizzata può essere più efficiente da calcolare e permette di descrivere facilmente l’inverso della trasformazione. Possiamo definire la trasformazione CLR generalizzata asclrp(y)=(logy1gp(y), ⋯, logyDgp(y)).
La trasformazione ILR generalizzata può quindi essere scritta asy∗=ilrp(y)=clrp(y) diag(p)ΨT
con l’elemento ijth della matrice Ψ dato daψij={+1ni+ni+ni+ni+ni-ni++ni-if θij=+1-1ni-ni+ni+ni-ni++ni-if θij=-10if θij=0 .
Con questi componenti definiti l’inverso della trasformazione ILR generalizzata può essere scritto come 𝒞[y]=ilrp-1(y∗)=𝒞[exp(y∗Ψ)] e x= 𝒞[ilrp-1(y∗)p].

Figura 5.Figura 5. Rappresentazione a matrice di segni di un albero filogenetico.Un albero binario(a sinistra) può essere rappresentato da una matrice di segni(a destra) indicata con Θ.DOI:
http://dx.doi.org/10.7554/eLife.21887.015
Trebbiatura morbida attraverso la ponderazione del taxa
Facciamo uso di questo ILR generalizzato trasformando a peso ridotto l’influenza dei taxa con molti conteggi a zero e quasi zero in quanto questi sono meno affidabili e quindi più variabili(Good, 1956). La nostra scelta dei pesi dei taxa è un euristico che combina moltiplicativamente due termini: una misura della tendenza centrale dei conteggi, come la media o la mediana dei conteggi grezzi per un taxon attraverso gli N campioni in un dataset; e, la norma del vettore delle abbondanze relative di un taxon attraverso gli N campioni in un dataset. Aggiungiamo questo termine della norma del vettore per pesare i taxa in base alla loro specificità del sito. Studi preliminari hanno dimostrato che la media geometrica dei conteggi (con uno pseudoconteggio aggiunto per evitare l’asimmetria rispetto ai valori zero) superava sia la media aritmetica che la mediana come misura della tendenza centrale dei conteggi (dati non mostrati). Inoltre, mentre sia la norma euclidea che la norma Aitchison hanno migliorato le prestazioni preliminari del benchmark rispetto all’uso della sola media geometrica, in un caso (classificazione con macchina vettoriale di supporto sul set di dati dei pattern globali), la norma euclidea ha ampiamente superato la norma Aitchison(file supplementare 1). Pertanto, il nostro schema di ponderazione taxa scelto utilizza la media geometrica per i tempi della norma euclidea:pj=(cj1+1)⋅…⋅(cjN+1)N⋅‖xj‖.
Si noti che aggiungiamo il pedice j alla destra dell’equazione di cui sopra per sottolineare che questo è calcolato rispetto ad un singolo taxon attraverso i campioni N in un set di dati. Come previsto, questo schema tendeva ad assegnare pesi più piccoli ai taxa nei nostri benchmark con più conteggi di zero e quasi zero(Figura 2-figure supplement 1). Nonostante la loro natura euristica, abbiamo scoperto che i nostri pesi scelti forniscono miglioramenti delle prestazioni rispetto ai pesi alternativi (o alla loro mancanza) misurati dai nostri compiti di benchmark(file supplementare 1).
Il nostro schema di ponderazione dei taxa integra l’uso di pseudo-conti e rappresenta una soglia morbida sui taxa a bassa abbondanza. Più in generale, queste ponderazioni dei taxa rappresentano una forma di informazione preventiva sull’importanza di ogni taxa. Notiamo che se le informazioni biologiche precedenti suggeriscono di permettere a specifici taxa di influenzare più (o meno) fortemente la trasformazione del PhILR, tale ponderazione potrebbe essere ottenuta per il taxon j aumentando (o diminuendo) il pj.
Incorporare le lunghezze dei rami
Oltre a utilizzare la connettività dell’albero filogenetico per dettare lo schema di suddivisione dei bilanci ILR, le informazioni sulla lunghezza dei rami possono essere incorporate nello spazio trasformato scalando linearmente i bilanci ILR (yi*) in base alla distanza tra i clades vicini. Chiamiamo questa scalatura in base alla distanza filogenetica “ponderazione della lunghezza dei rami”. In particolare, per ogni coordinata yi*, corrispondente al nodo i utilizziamo la transformyi*,blw=yi*∙f(di+,di-)
dove di± rappresentano le lunghezze dei rami dei due figli diretti del nodo i. Quando f(di+,di-)=1, le coordinate non sono ponderate per le lunghezze dei rami. La forma di questa trasformazione è stata scelta in modo che i pesi di±, influenzino solo la coordinata corrispondente (yi*,blw).
Abbiamo anche studiato l’effetto dell’utilizzo di f(di+,di-)=1, f(di+,di-)=di+++di-, e sulla base dei risultati di Chen et al. (2012), f(di+,di-)=di+++di- sulla performance del benchmark. Quando accoppiata con i pesi taxa specificati sopra, la radice quadrata delle distanze sommate aveva il rango più alto in 9 dei 12 compiti di classificazione supervisionati e 2 dei tre compiti basati sulla distanza(file supplementare 1). Sulla base di questi risultati, ad eccezione della nostra analisi della varianza dell’equilibrio rispetto alla profondità filogenetica (vedi sotto), la radice quadrata delle distanze sommate è stata utilizzata in tutte le nostre analisi.
Implementazione
La trasformazione PhILR, così come l’incorporazione della lunghezza delle filiali e della ponderazione dei taxa è stata implementata nel linguaggio di programmazione R come pacchetto philr disponibile all’indirizzo https://bioconductor.org/packages/philr/.
Set di dati e preelaborazione
Tutti i pretrattamenti dei dati sono stati effettuati nel linguaggio di programmazione R utilizzando il pacchetto phyloseq per l’analisi dei dati del censimento dei microbiomi(McMurdie e Holmes, 2013) e i pacchetti ape (Paradis et al., 2004) e phangorn(Schliep, 2011) per l’analisi degli alberi filogenetici.
Acquisizione dei dati
Abbiamo scelto di utilizzare le tabelle OTU pubblicate in precedenza, le classificazioni tassonomiche e le filogenesi come punto di partenza per le nostre analisi. Il set di dati del Progetto sui Microbiomi Umani (HMP) è stato ottenuto dal QIIME Community Profiling Pipeline applicato alle letture di alta qualità della regione v3-5, disponibile all’indirizzo http://hmpdacc.org/HMQCP/. Il dataset Global Patterns è stato originariamente pubblicato su Caporaso, et al.(Caporaso et al., 2011) e viene fornito con il pacchetto phyloseq R(McMurdie e Holmes, 2013). Il dataset Costello Skin Sites (CSS) è un sottoinsieme del dataset raccolto da Costello et al.(Costello et al., 2009) con i soli campioni provenienti da siti cutanei. Questo sottoinsieme di pelle è stato introdotto come punto di riferimento per il machine learning supervisionato da Knights et al.(Knights et al., 2011) e può essere ottenuto dahttp://www.knightslab.org/data.
Tabella OTU pre-elaborazione
In accordo con la prassi generale, abbiamo eseguito un livello minimo di filtraggio delle tabelle OTU per tutti i set di dati utilizzati nei benchmark e nelle analisi. A causa delle differenze nella profondità di sequenziamento, nella metodologia di sequenziamento e nel numero e nella diversità dei campioni tra i dataset, le soglie di filtraggio sono state impostate in modo indipendente per ogni dataset. Per il dataset HMP, abbiamo inizialmente rimosso i campioni con meno di 1000 conteggi per imitare le analisi precedenti(Human Microbiome Project Consortium, 2012). Abbiamo inoltre rimosso le OTU che non sono state viste con più di tre conteggi in almeno l’1% dei campioni. Il pretrattamento della tabella delle OTU Global Patterns ha seguito i metodi descritti in McMurdie and Holmes(McMurdie and Holmes, 2013). In particolare, sono state rimosse le OTU che non sono state viste con più di tre conteggi in almeno il 20% dei campioni, la profondità di sequenziamento di ogni campione è stata standardizzata in base all’abbondanza della profondità di campionamento mediana, e infine sono state rimosse le OTU con un coefficiente di variazione ≤3,0. Il set di dati CSS aveva una profondità di sequenziamento inferiore rispetto agli altri due set di dati; abbiamo scelto di filtrare le OTU che non sono state viste con più di 10 conteggi tra i campioni di pelle. La trasformazione PhILR, e più in generale i nostri risultati di benchmarking nella Figura 2b e C, sono stati robusti per variare le nostre strategie di filtraggio(file supplementare 2).
Filogenesi di pretrattamento
Per ogni set di dati, la filogenesi è stata potata in modo da includere solo i taxa rimasti dopo il pretrattamento della tabella OTU. Ad eccezione del dataset Global Patterns, che era già radicato, abbiamo scelto di radicare le filogenie specificando manualmente un outgroup. Per il dataset HMP è stato scelto come outgroup il phylum Euryarchaeota. Per il dataset CSS, l’albero è stato radicato con OTU 12871 (dal phylum Plantomycetes) come outgroup. Per tutte e tre le filogenie, le eventuali multichotomie sono state risolte con la funzione multi2di del pacchetto ape che sostituisce le multichotomie con una serie di dicotomie con uno (o più) rami di lunghezza zero.
Sostituzione e normalizzazione dello zero
Prima della trasformazione di PhILR è stato aggiunto uno pseudoconteggio di 1 per evitare di prendere i log-rati con conteggi a zero. Abbiamo trovato che i nostri risultati di benchmarking erano solidi per modificare il valore di questo pseudoconteggio da 1 a 2, 3 o 10(file supplementare 1).
Raggruppamento dei siti di campionamento
Per semplificare le analisi successive, i campioni HMP della piega retroauricolare destra e sinistra e i campioni della fossa antecubitale destra e sinistra sono stati raggruppati, rispettivamente, come l’analisi preliminare PERMANOVA ha suggerito che questi siti erano indistinguibili (dati non mostrati).
Benchmarking
Analisi basata sulla distanza/dissimilarità
La distanza tra i campioni nello spazio trasformato in PhILR è stata calcolata utilizzando la distanza euclidea. Tutte le altre misure di distanza sono state calcolate utilizzando phyloseq sui dati preprocessati senza aggiungere uno pseudoconteggio. L’analisi delle coordinate di principio è stata eseguita per la visualizzazione utilizzando phyloseq. PERMANOVA è stata eseguita utilizzando la funzione adonis del pacchetto R vegan (v2.3.4). Il valore R2 del modello montato è stato preso come metrica delle prestazioni. Gli errori standard sono stati calcolati utilizzando il ricampionamento bootstrap con 100 campioni ciascuno. Le differenze tra le prestazioni della distanza euclidea nello spazio trasformato di PhILR e quella di ogni altra misura di distanza o di difformità su un determinato compito sono state testate usando test t su due lati e sono state prese in considerazione le prove di ipotesi multiple usando la correzione FDR.
Classificazione supervisionata
Le prestazioni, misurate in base all’accuratezza della classificazione, dei dati trasformati di PhILR sono state confrontate con i dati preprocessati utilizzando una delle due strategie standard per la normalizzazione della profondità di sequenziamento: i dati preprocessati sono stati trasformati in abbondanze relative(ad esempio, ogni campione è stato normalizzato ad una somma costante di 1; grezzo); oppure, è stato aggiunto uno pseudoconteggio di 1, i dati sono stati trasformati in abbondanze relative e, infine, le abbondanze relative sono state trasformate in log-transformate(log).
Tutto l’apprendimento supervisionato è stato implementato in Python utilizzando le seguenti librerie: Scikit-learn (v0.17.1), numpy (v1.11.0) e panda (v0.17.1). Sono stati utilizzati quattro classificatori: regressione logistica penalizzata, classificazione vettoriale di supporto con kernel RBF, classificazione forestale casuale e classificazione k-nearest-neighbors. Ogni compito di classificazione è stato valutato utilizzando la media e la varianza dell’accuratezza del test su 10 split di test/treno randomizzati (30/70) che hanno preservato la percentuale di campioni di ogni classe ad ogni split. Per ogni classificatore, per ogni split, sono stati impostati i seguenti parametri utilizzando la convalida incrociata sul set di training. Regressione logistica e classificazione vettoriale di supporto: il parametro ‘C’ è stato permesso di variare da 10-3 a 103 e la classificazione multi-classe è stata gestita con una perdita di una Vs. Inoltre, per la regressione logistica, la sanzione poteva essere l1 o l2. Classificazione K-nearest-neighbors: l’argomento “pesi” è stato impostato su “distanza”. Classificazione casuale delle foreste: ogni foresta conteneva 30 alberi e l’argomento ‘max_caratteristiche’ poteva variare tra 0.1 e 1. Tutti gli altri parametri erano impostati su valori predefiniti. A causa delle piccole dimensioni del set di dati Global Patterns, il compito di classificazione supervisionato è stato semplificato per distinguere i campioni umani da quelli non umani. Le differenze tra l’accuratezza di ciascun metodo in ogni compito sono state testate utilizzando test a t su due lati e sono state prese in considerazione le prove di ipotesi multiple utilizzando la correzione FDR.
Identificazione delle bilance che distinguono i siti
Per identificare un insieme sparso di saldi che distinguono i siti di campionamento, mentre si tiene conto delle dipendenze tra i saldi annidati, si adatta un modello di regressione multinomiale con una penalità l1 raggruppata utilizzando il pacchetto R glmnet(v2.0.5). Il termine di penalizzazione lambda è stato impostato ispezionando visivamente le uscite del modello per una chiara separazione del sito del corpo (lambda = 0,1198). Ciò ha portato a 35 bilanci con coefficienti di regressione non zero. La visualizzazione dell’albero filogenetico è stata effettuata utilizzando il pacchetto R ggtree(Yu et al., 2017).
Varianza e profondità
Per ridurre la probabilità che la nostra analisi della varianza dell’equilibrio e della profondità filogenetica fosse influenzata da artefatti statistici, abbiamo modificato la nostra trasformazione del PhILR in diversi modi. In primo luogo, abbiamo omesso i pesi della lunghezza dei rami( cioè abbiamo impostato f(di+,di-)=1) in quanto questi possono variare in modo non casuale in funzione della profondità filogenetica. In secondo luogo, abbiamo anche previsto che qualsiasi metodo di sostituzione dello zero avrebbe probabilmente portato a misure di varianza più basse, che potrebbero avere maggiori effetti sulle bilance più vicine alle punte dell’albero. Abbiamo quindi omesso i pesi dei taxa e la sostituzione dello zero; abbiamo invece utilizzato soglie di filtraggio più severe e abbiamo calcolato i valori delle bilance in base a conteggi diversi dallo zero. In pratica, abbiamo utilizzato le seguenti soglie di filtraggio per ogni sito del corpo, i taxa presenti in meno del 20% dei campioni di quel sito sono stati esclusi e successivamente sono stati esclusi i campioni che avevano meno di 50 conteggi totali. Per calcolare i valori di bilancio basati su conteggi non zero abbiamo mantenuto i bilanci che soddisfacevano i seguenti criteri: il termine gp(yi+)/gp(yi-) aveva conteggi non zero da alcuni taxa all’interno della sottocomposizione yi+ (formata dai taxa che discendono dal clade +1 del nodo i) e da alcuni altri taxa all’interno della sottocomposizione yi- (formata dai taxa che discendono dal clade -1 del nodo i) in almeno 40 campioni provenienti da quel sito corporeo. Riteniamo che queste due modifiche al PhILR abbiano portato ad un’analisi più conservativa della varianza dell’equilibrio rispetto alla profondità filogenetica, ma probabilmente non sono ottimali in altre situazioni.
Per indagare la relazione complessiva tra la varianza dell’equilibrio e la profondità filogenetica abbiamo utilizzato la regressione lineare. La profondità di un equilibrio nell’albero è stata calcolata come distanza filogenetica media tra le punte discendenti (d). Per un dato sito corporeo il seguente modello era adatto:logvar(y∗) =βlogd+ α
dove d rappresenta la distanza media da una bilancia alle punte discendenti. Ci siamo quindi proposti di testare l’ipotesi nulla che β=0, o che la varianza del rapporto log-rapporto tra due clades fosse invariante alla distanza dei due clades dal loro antenato comune più recente. Per ogni sito è stata costruita una distribuzione nulla per β mediante permutazioni delle etichette di punta dell’albero filogenetico. Per ogni permutazione delle etichette, l’albero risultante è stato utilizzato per trasformare i dati ed è stato stimato il β. Abbiamo scelto questo schema di permutazione per garantire che la varianza crescente che abbiamo visto con la crescente vicinanza di un equilibrio alla radice non fosse dovuta al fatto che gli equilibri più profondi avevano più punte discendenti, un artefatto di scalatura della varianza con abbondanza media, o a distorsioni introdotte a causa della nostra manipolazione degli zeri. Inoltre, per ogni sito del corpo, abbiamo trovato che la distribuzione nulla per β era simmetrica circa β=0, il che supporta ulteriormente che la varianza dell’equilibrio dipende dalla profondità filogenetica attraverso un meccanismo biologico e non attraverso un artefatto statistico (Figura 4-figuresupplement 3). Due valori p coda sono stati calcolati per β sulla base di 20000 campioni da ogni sito di distribuzione nullo rispettivo di ogni sito. La correzione FDR è stata applicata per tener conto dei test di ipotesi multiple tra i siti del corpo.
Per visualizzare le tendenze locali nel rapporto tra la varianza di equilibrio e la profondità filogenetica, una regressione LOESS è stata adattata indipendentemente per ogni sito del corpo. Ciò è stato fatto utilizzando la funzione geom_smooth del pacchetto R ggplot2 (v2.1.0) con parametri predefiniti.
I dati e il codice necessari per riprodurre la nostra analisi della varianza dell’equilibrio rispetto alla profondità filogenetica sono forniti nella Figura 4 dati 1 e nella Figura 4 codice 1 rispettivamente.
Integrazione delle informazioni tassonomiche
La tassonomia è stata assegnata alle OTU nel set di dati HMP usando lo script assign_taxonomy.py di Qiime (v1.9.1) per chiamare uclust (v1.2.22) con parametri di default usando le sequenze rappresentative delle OTU ottenute come descritto sopra. Gli identificatori tassonomici sono stati assegnati ai due clades discendenti di una data bilancia separatamente usando un semplice schema di voto e combinati in un unico nome per quella bilancia. Lo schema di voto avviene come segue: (1) per un determinato clade, l’intera tabella tassonomica è stata sottoinsieme per contenere solo le UTU presenti in quel clade (2) a partire dal rango tassonomico più alto, la tabella tassonomica del sottoinsieme è stata controllata per vedere se un qualsiasi identificatore di specie rappresentava ≥95% delle voci della tabella in quel rango tassonomico, se così è stato preso quell’identificatore come etichetta tassonomica per il clade (3) se non è stato trovato un identificatore di consenso, la tabella è stata controllata al rango tassonomico successivo più specifico.
Le profondità filogenetiche mediane per ogni rango tassonomico sono state stimate decorando prima un albero filogenetico con informazioni tassonomiche utilizzando tax2tree (v1.0)(McDonald et al., 2012). Per un dato rango tassonomico è stata calcolata la distanza media delle punte per ogni nodo interno in possesso di un’etichetta che terminava in quel rango. La mediana di queste distanze è stata utilizzata per visualizzare una stima della profondità filogenetica di quel determinato rango. Questo calcolo della profondità filogenetica mediana dei diversi ranghi tassonomici è stato fatto separatamente per ogni sito corporeo.
I dati e il codice necessari per riprodurre l’assegnazione tassonomica e la stima della profondità filogenetica mediana per ogni rango tassonomico sono inclusi rispettivamente nella Figura 4 dati fonte 1 e nella Figura 4 codice fonte 1.
References
- Aas JA, Paster BJ, Stokes LN, Olsen I, Dewhirst FE. Defining the normal bacterial flora of the oral cavity. Journal of Clinical Microbiology. 2005; 43:5721-5732. DOI | PubMed
- Aitchison J. The Statistical Analysis of Compositional Data. Chapman and Hall: London; New York; 1986.
- Anders S, Huber W. Differential expression analysis for sequence count data. Genome Biology. 2010; 11DOI | PubMed
- Bacon-Shone J. Compositional Data Analysis. John Wiley & Sons, Ltd: Hoboken, NJ; 2011.
- Bear J, Billheimer D. A logistic normal mixture model for compositional data allowing essential zeros. Austrian Journal of Statistics. 2016; 45:3-23. DOI
- Billheimer D, Guttorp P, Fagan WF. Statistical interpretation of species composition. Journal of the American Statistical Association. 2001; 96:1205-1214. DOI
- Blaser MJ, Falkow S. What are the consequences of the disappearing human Microbiota?. Nature Reviews Microbiology. 2009; 7:887-894. DOI | PubMed
- Britanova OV, Putintseva EV, Shugay M, Merzlyak EM, Turchaninova MA, Staroverov DB, Bolotin DA, Lukyanov S, Bogdanova EA, Mamedov IZ, Lebedev YB, Chudakov DM. Age-related decrease in TCR repertoire diversity measured with deep and normalized sequence profiling. The Journal of Immunology. 2014; 192:2689-2698. DOI | PubMed
- Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Lozupone CA, Turnbaugh PJ, Fierer N, Knight R. Global patterns of 16S rRNA diversity at a depth of millions of sequences per sample. PNAS. 2011; 108 Suppl 1:4516-4522. DOI | PubMed
- Chen J, Bittinger K, Charlson ES, Hoffmann C, Lewis J, Wu GD, Collman RG, Bushman FD, Li H. Associating microbiome composition with environmental covariates using generalized UniFrac distances. Bioinformatics. 2012; 28:2106-2113. DOI | PubMed
- Chen J, Li H. Variable selection for sparse Dirichlet-multinomial regression with an application to microbiome data analysis. The Annals of Applied Statistics. 2013; 7:418-442. DOI | PubMed
- Costello EK, Lauber CL, Hamady M, Fierer N, Gordon JI, Knight R. Bacterial community variation in human body habitats across space and time. Science. 2009; 326:1694-1697. DOI | PubMed
- Culley AI, Lang AS, Suttle CA. Metagenomic analysis of coastal RNA virus communities. Science. 2006; 312:1795-1798. DOI | PubMed
- De Filippo C, Cavalieri D, Di Paola M, Ramazzotti M, Poullet JB, Massart S, Collini S, Pieraccini G, Lionetti P. Impact of diet in shaping gut Microbiota revealed by a comparative study in children from Europe and rural Africa. PNAS. 2010; 107:14691-14696. DOI | PubMed
- Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barcelo-Vidal C. Isometric logratio transformations for compositional data analysis. Mathematical Geology. 2003; 35:279-300. DOI
- Egozcue JJ, Pawlowsky-Glahn V. Groups of parts and their balances in compositional data analysis. Mathematical Geology. 2005; 37:795-828. DOI
- Egozcue JJ, Pawlowsky-Glahn V. Changing the reference measure in the simplex and its weighting effects. Austrian Journal of Statistics. 2016; 45:25-44. DOI
- Fang H, Huang C, Zhao H, Deng M. CCLasso: correlation inference for compositional data through lasso. Bioinformatics. 2015; 31:3172-3180. DOI | PubMed
- Faust K, Sathirapongsasuti JF, Izard J, Segata N, Gevers D, Raes J, Huttenhower C. Microbial co-occurrence relationships in the human microbiome. PLoS Computational Biology. 2012; 8:e1002606. DOI | PubMed
- Fernandes AD, Reid JN, Macklaim JM, McMurrough TA, Edgell DR, Gloor GB. Unifying the analysis of high-throughput sequencing datasets: characterizing RNA-seq, 16S rRNA gene sequencing and selective growth experiments by compositional data analysis. Microbiome. 2014; 2:15. DOI | PubMed
- Finucane MM, Sharpton TJ, Laurent TJ, Pollard KS. A taxonomic signature of obesity in the microbiome? getting to the guts of the matter. PLoS One. 2014; 9DOI | PubMed
- Friedman J, Alm EJ. Inferring correlation networks from genomic survey data. PLoS Computational Biology. 2012; 8DOI | PubMed
- Fukuyama J, McMurdie PJ, Dethlefsen L, Relman DA, Holmes S. Pacific Symposium on Biocomputing. NIH Public Access; 2012.
- Gloor GB, Macklaim JM, Vu M, Fernandes AD. Compositional uncertainty should not be ignored in high-throughput sequencing data analysis. Austrian Journal of Statistics. 2016a; 45DOI
- Gloor GB, Wu JR, Pawlowsky-Glahn V, Egozcue JJ. It’s all relative: analyzing microbiome data as compositions. Annals of Epidemiology. 2016b; 26:322-329. DOI | PubMed
- Good IJ. On the estimation of small frequencies in Contingency-Tables. Journal of the Royal Statistical Society Series B-Statistical Methodology. 1956; 18:113-124.
- Grice EA, Segre JA. The skin microbiome. Nature Reviews Microbiology. 2011; 9:244-253. DOI | PubMed
- Human Microbiome Project Consortium. Structure, function and diversity of the healthy human microbiome. Nature. 2012; 486:207-214. DOI | PubMed
- Hunt DE, David LA, Gevers D, Preheim SP, Alm EJ, Polz MF. Resource partitioning and sympatric differentiation among closely related bacterioplankton. Science. 2008; 320:1081-1085. DOI | PubMed
- Jackson DA. Compositional data in community ecology: the paradigm or peril of proportions?. Ecology. 1997; 78:929-940. DOI
- Janda JM, Abbott SL. 16s rRNA gene sequencing for bacterial identification in the diagnostic laboratory: pluses, perils, and pitfalls. Journal of Clinical Microbiology. 2007; 45:2761-2764. DOI | PubMed
- Knights D, Costello EK, Knight R. Supervised classification of human Microbiota. FEMS Microbiology Reviews. 2011; 35:343-359. DOI | PubMed
- Kurtz ZD, Müller CL, Miraldi ER, Littman DR, Blaser MJ, Bonneau RA. Sparse and compositionally robust inference of microbial ecological networks. PLOS Computational Biology. 2015; 11DOI | PubMed
- La Rosa PS, Brooks JP, Deych E, Boone EL, Edwards DJ, Wang Q, Sodergren E, Weinstock G, Shannon WD. Hypothesis testing and power calculations for taxonomic-based human microbiome data. PLoS ONE. 2012; 7DOI | PubMed
- Lee SC, Tang MS, Lim YA, Choy SH, Kurtz ZD, Cox LM, Gundra UM, Cho I, Bonneau R, Blaser MJ, Chua KH, Loke P. Helminth colonization is associated with increased diversity of the gut Microbiota. PLoS Neglected Tropical Diseases. 2014; 8DOI | PubMed
- Levy R, Borenstein E. Metabolic modeling of species interaction in the human microbiome elucidates community-level assembly rules. PNAS. 2013; 110:12804-12809. DOI | PubMed
- Ley RE, Hamady M, Lozupone C, Turnbaugh PJ, Ramey RR, Bircher JS, Schlegel ML, Tucker TA, Schrenzel MD, Knight R, Gordon JI. Evolution of mammals and their gut microbes. Science. 2008; 320:1647-1651. DOI | PubMed
- Lê Cao KA, Costello ME, Lakis VA, Bartolo F, Chua XY, Brazeilles R, Rondeau P. MixMC: a multivariate statistical framework to gain insight into microbial communities. PLoS One. 2016; 11DOI | PubMed
- Li H. Microbiome, metagenomics, and high-dimensional compositional data analysis. Annual Review of Statistics and Its Application. 2015; 2:73-94. DOI
- Lin W, Shi P, Feng R, Li H. Variable selection in regression with compositional covariates. Biometrika. 2014; 101:785-797. DOI
- Lovell D, Müller W, Taylor J, Zwart A, Helliwell C. Compositional Data Analysis: Theory and Applications. John Wiley & Sons, Ltd: Hoboken, NJ; 2011.
- Lovell D, Pawlowsky-Glahn V, Egozcue JJ, Marguerat S, Bähler J. Proportionality: a valid alternative to correlation for relative data. PLOS Computational Biology. 2015; 11DOI | PubMed
- Lozupone C, Knight R. UniFrac: a new phylogenetic method for comparing microbial communities. Applied and Environmental Microbiology. 2005; 71:8228-8235. DOI | PubMed
- Mager DL, Ximenez-Fyvie LA, Haffajee AD, Socransky SS. Distribution of selected bacterial species on intraoral surfaces. Journal of Clinical Periodontology. 2003; 30:644-654. DOI | PubMed
- Mandal S, Van Treuren W, White RA, Eggesbø M, Knight R, Peddada SD. Analysis of composition of microbiomes: a novel method for studying microbial composition. Microbial Ecology in Health & Disease. 2015; 26:27663. DOI | PubMed
- Martın-Fernandez JA, Palarea-Albaladejo J, Olea RA. Compositional Data Analysis: Theory and Applications. John Wiley & Sons, Ltd: Hoboken, NJ; 2011.
- Martin-Fernandez J-A, Hron K, Templ M, Filzmoser P, Palarea-Albaladejo J. Bayesian-multiplicative treatment of count zeros in compositional data sets. Statistical Modelling. 2015; 15:134-158. DOI
- Martiny JB, Jones SE, Lennon JT, Martiny AC. Microbiomes in light of traits: a phylogenetic perspective. Science. 2015; 350DOI | PubMed
- Matsen FA. Phylogenetics and the human microbiome. Systematic Biology. 2015; 64:e26-e41. DOI | PubMed
- McDonald D, Price MN, Goodrich J, Nawrocki EP, DeSantis TZ, Probst A, Andersen GL, Knight R, Hugenholtz P. An improved greengenes taxonomy with explicit ranks for ecological and evolutionary analyses of Bacteria and archaea. The ISME Journal. 2012; 6:610-618. DOI | PubMed
- McMurdie PJ, Holmes S. Phyloseq: an R package for reproducible interactive analysis and graphics of microbiome census data. PLoS One. 2013; 8DOI | PubMed
- McMurdie PJ, Holmes S. Waste not, want not: why rarefying microbiome data is inadmissible. PLoS Computational Biology. 2014; 10DOI | PubMed
- Moeller AH, Caro-Quintero A, Mjungu D, Georgiev AV, Lonsdorf EV, Muller MN, Pusey AE, Peeters M, Hahn BH, Ochman H. Cospeciation of gut microbiota with hominids. Science. 2016; 353:380-382. DOI | PubMed
- Morton JT, Sanders J, Quinn RA, McDonald D, Gonzalez A, Vázquez-Baeza Y, Navas-Molina JA, Song SJ, Metcalf JL, Hyde ER, Lladser M, Dorrestein PC, Knight R. Balance trees reveal microbial niche differentiation. mSystems. 2017; 2:e00162-16. DOI | PubMed
- Paradis E, Claude J, Strimmer K. APE: analyses of phylogenetics and evolution in R language. Bioinformatics. 2004; 20:289-290. DOI | PubMed
- Paulson JN, Stine OC, Bravo HC, Pop M. Differential abundance analysis for microbial marker-gene surveys. Nature Methods. 2013; 10:1200-1202. DOI | PubMed
- Pawlowsky-Glahn V, Buccianti A. Compositional Data Analysis: Theory and Applications. John Wiley & Sons, Ltd: Hoboken, NJ; 2011.
- Pawlowsky-Glahn V, Egozcue JJ, Tolosana-Delgado R. Modeling and Analysis of Compositional Data. John Wiley & Sons, Ltd: Hoboken, NJ; 2015.
- Pawlowsky-Glahn V, Egozcue JJ. Exploring compositional data with the CoDa-Dendogram. Austrian Journal of Statistics. 2011; 40:103-113.
- Purdom E. Analysis of a data matrix and a graph: metagenomic data and the phylogenetic tree. The Annals of Applied Statistics. 2011; 5:2326-2358. DOI
- Rakoff-Nahoum S, Foster KR, Comstock LE. The evolution of cooperation within the gut microbiota. Nature. 2016; 533:255-259. DOI | PubMed
- Roth A, Khattra J, Yap D, Wan A, Laks E, Biele J, Ha G, Aparicio S, Bouchard-Côté A, Shah SP. PyClone: statistical inference of clonal population structure in Cancer. Nature Methods. 2014; 11:396-398. DOI | PubMed
- Schliep KP. Phangorn: phylogenetic analysis in R. Bioinformatics. 2011; 27:592-593. DOI | PubMed
- Smillie CS, Smith MB, Friedman J, Cordero OX, David LA, Alm EJ. Ecology drives a global network of gene exchange connecting the human microbiome. Nature. 2011; 480:241-244. DOI | PubMed
- Tsilimigras MC, Fodor AA. Compositional data analysis of the microbiome: fundamentals, tools, and challenges. Annals of Epidemiology. 2016; 26:330-335. DOI | PubMed
- van den Boogaart KG, Tolosana-Delgado R. Analyzing Compositional Data with R. Springer: New York; 2013.
- Větrovský T, Baldrian P. The variability of the 16S rRNA gene in bacterial genomes and its consequences for bacterial community analyses. PLoS One. 2013; 8DOI | PubMed
- Waldor MK, Tyson G, Borenstein E, Ochman H, Moeller A, Finlay BB, Kong HH, Gordon JI, Nelson KE, Dabbagh K, Smith H. Where next for microbiome research?. PLOS Biology. 2015; 13DOI | PubMed
- Wu GD, Chen J, Hoffmann C, Bittinger K, Chen YY, Keilbaugh SA, Bewtra M, Knights D, Walters WA, Knight R, Sinha R, Gilroy E, Gupta K, Baldassano R, Nessel L, Li H, Bushman FD, Lewis JD, Gd W. Linking long-term dietary patterns with gut microbial enterotypes. Science. 2011; 334:105-108. DOI | PubMed
- Yatsunenko T, Rey FE, Manary MJ, Trehan I, Dominguez-Bello MG, Contreras M, Magris M, Hidalgo G, Baldassano RN, Anokhin AP, Heath AC, Warner B, Reeder J, Kuczynski J, Caporaso JG, Lozupone CA, Lauber C, Clemente JC, Knights D, Knight R, Gordon JI. Human gut microbiome viewed across age and geography. Nature. 2012; 486:222-227. DOI | PubMed
- Yu G, Smith DK, Zhu H, Guan Y, Lam TT-Y. Ggtree : an r package for visualization and annotation of phylogenetic trees with their covariates and other associated data. Methods in Ecology and Evolution. 2017; 8:28-36. DOI
- Yuan K, Sakoparnig T, Markowetz F, Beerenwinkel N. BitPhylogeny: a probabilistic framework for reconstructing intra-tumor phylogenies. Genome Biology. 2015; 16DOI | PubMed
- Zaneveld JR, Lozupone C, Gordon JI, Knight R. Ribosomal RNA diversity predicts genome diversity in gut bacteria and their relatives. Nucleic Acids Research. 2010; 38:3869-3879. DOI | PubMed
Fonte
Silverman JD, Washburne AD, Mukherjee S, David LA, Fodor A, et al. () A phylogenetic transform enhances analysis of compositional microbiota data. eLife 6e21887. https://doi.org/10.7554/eLife.21887





