Abstract
Introduzione
La gamma di stimoli naturali che una persona o un animale incontra in un solo giorno è in costante evoluzione. Un esempio comune è quello di uscire da un cinema buio ed entrare in un atrio illuminato. Anche se l’illuminamento della luce può cambiare di tre ordini di grandezza tra queste due stanze, in pochi secondi siamo in grado di vedere chiaramente. Questa capacità può essere spiegata dal comportamento dei neuroni che codificano le informazioni sull’intensità della luce. I neuroni nella corteccia visiva primaria e nella retina codificano l’intensità della luce con le loro velocità di accensione(Kuffler, 1953; Hubel e Wiesel, 1962). Queste relazioni di sintonizzazione seguono tipicamente curve monotoniche tra le velocità di sparo di zero e le velocità di sparo massime dei neuroni (cioè la gamma dinamica dei neuroni). La risoluzione nella relazione è determinata dal numero di passi nel rateo di accensione che si possono distinguere. La risoluzione è una metrica di informazione ed è una funzione sia della pendenza della curva che della quantità di rumore nel rateo di cottura. Quando il livello di intensità della luce cambia dal teatro buio all’atrio luminoso, le curve di sintonia neurale si spostano e regolano le loro pendenze per fornire la risoluzione nella nuova gamma di intensità della luce(Shapley e Enroth-Cugell, 1984; Ohzawa et al., 1985; Smirnakis et al., 1997; Ohzawa et al., 1982; Harris et al., 2000). Questo fenomeno è comunemente chiamato adattamento della gamma dinamica. Oltre a questo esempio nel sistema visivo, l’adattamento della gamma dinamica è stato documentato anche in altre aree sensoriali, compresi i sistemi uditivi(Kvale e Schreiner, 2004; Ulanovsky et al., 2004; Dean et al., 2005; Nagel e Doupe, 2006; Rabinowitz et al., 2011) e somatosensoriali(Maravall et al., 2007; Katz et al., 2006). Questo fenomeno è stato descritto come l’ottimizzazione della trasmissione di informazioni sugli stimoli in ingresso entro i limitati intervalli di sintonia dei neuroni(Brenner et al., 2000; Fairhall et al., 2001; Wark et al., 2007; Atick, 2011).
Nei sistemi sensoriali, le variabili di input significative possono essere descritte concretamente. Nei sistemi motori, i parametri controllati sono ancora in discussione. La forza è stata una delle prime variabili di uscita descritte, e molti studi hanno dimostrato che i tassi di sparo dei neuroni nella corteccia motoria primaria (M1) modulano con i livelli di forza di uscita nelle relazioni monotoniche(Evarts, 1966, 1968; Humphrey et al., 1970; Hepp-Reymond et al., 1978; Georgopoulos et al., 1992). Humphrey et al. hanno brevemente notato nel loro lavoro che il valore dei coefficienti di regressione che mettono in relazione l’attività motoneuronale con la forza in scala con la gamma delle forze nel loro compito(Humphrey et al., 1970). Questo risultato potrebbe essere spiegato dall’adattamento della gamma dinamica. Come la gamma di stimoli (forze di uscita) cambia, la pendenza della curva di sintonia cambia per codificare la gamma delle forze all’interno di una gamma limitata di velocità di sparo. Hepp-Reymond et al. hanno successivamente esplorato questo fenomeno in modo più dettagliato(Hepp-Reymond et al., 1999). Essi hanno dimostrato che i neuroni corticali motori che codificano la forza durante un compito di pizzicamento isometrico subiscono un adattamento della gamma dinamica con cambiamenti nel contesto del compito e delle aspettative del contesto del compito.
In lavori successivi, la direzione del movimento del braccio ha ricevuto l’attenzione come variabile controllata(Georgopoulos et al., 1982, 1988; Schwartz et al., 1988). Questi studi hanno dimostrato una relazione di cosine-tuning tra la direzione del movimento e i tassi di tiro neuronale. Ogni unità è stata descritta come avente una direzione preferenziale in cui la velocità di sparo era massima per i movimenti in quella direzione e minima per i movimenti in direzione opposta. In questo modello classico, le velocità di sparo modulano linearmente tra la velocità minima e massima con il coseno dell’angolo tra la direzione di movimento e la direzione preferita. Questo modello di sintonia è stato dimostrato per i movimenti sia nel braccio bidimensionale che in quello tridimensionale. In particolare, il modello prevede un intervallo inferiore nei ratei di tiro per i movimenti 2D rispetto ai movimenti 3D quando la direzione preferita non è complanare con lo spazio di movimento 2D. Ciò solleva la questione unica di sapere se il cambiamento delle statistiche dei movimenti in uscita da movimenti 3D a movimenti puramente 2D porterebbe ad un adattamento della gamma dinamica.
È difficile studiare queste differenze con i movimenti reali del braccio. Indipendentemente dal contesto 2D o 3D, i movimenti del braccio sono ancora all’interno di un ambiente dinamico soggetto a molti fattori esterni tra cui la gravità, l’inerzia e la cinematica del braccio a cui i neuroni possono modulare. Nel tentativo di imporre una relazione diretta tra la velocità di sparo e la direzione del movimento, abbiamo studiato questa questione utilizzando un’interfaccia cervello-computer (BCI). Essenzialmente, il compito della BCI ci ha permesso di annullare questi fattori esterni e di indagare puramente le differenze di sintonia tra i movimenti 3D e 2D. Abbiamo addestrato le scimmie a muovere un cursore sullo schermo di un computer 3D sotto il controllo del cervello, utilizzando un algoritmo vettoriale di popolazione (PVA) o un decodificatore di stimolazione lineare ottimale (OLE) (Chaseet al., 2009). Le scimmie controllavano il cursore modulando le velocità di fuoco dei neuroni registrati nella corteccia motoria mentre eseguivano un classico compito di centratura sia in ambiente 2D che 3D. Abbiamo scoperto che i neuroni all’interno di M1 subiscono un cambiamento nella sintonia tra il contesto 2D e 3D. Abbiamo quindi sfruttato la simultaneità delle registrazioni per testare diverse ipotesi sui meccanismi di questi cambiamenti basati sulla popolazione. Abbiamo scoperto che i risultati sono coerenti con l’adattamento della gamma dinamica.
Risultati
Due macachi Rhesus di sesso maschile impiantati con array dello Utah sono stati addestrati per eseguire compiti di centratura 2D e 3D in realtà virtuale, sotto controllo cerebrale(Figura 1A,B). Per mappare l’attività neurale in base al movimento del cursore, si è supposto che l’attività di ogni unità seguisse un modello di sintonizzazione del coseno in 3D. Con i modelli di attività neurale montati, il movimento del cursore è stato aggiornato online ogni 33 ms con le uscite dei decodificatori come descritto più dettagliatamente nella sezione Materiali e metodi. Per il compito 2D, il componente z del movimento decodificato è stato azzerato per limitare il movimento al piano xy. C’erano 26 obiettivi nel contesto 3D e 16 obiettivi nel contesto 2D. I due set di target includevano otto target comuni, permettendo un confronto diretto della sintonizzazione tra i due contesti dei task(Figura 1C,D). Abbiamo analizzato 18 sessioni da Monkey A e 11 da Monkey C. La nostra analisi si è concentrata sulle unità che hanno contribuito al movimento del cursore per entrambi i contesti. La dimensione media di questa popolazione sovrapposta è stata di 26,4 unità per la Scimmia A (min: 13; max: 32) e 37,2 unità per la Scimmia C (min: 30; max: 45). Per cinque sessioni di registrazione della Scimmia A e 4 della Scimmia C, l’intera popolazione di unità che controllava il movimento del cursore era identica tra i due contesti. La dimensione media della popolazione per queste sessioni era di 28,6 unità per la Scimmia A (min: 26; max: 32) e 39,5 unità per la Scimmia C (min: 33; max: 45). Sei unità che sembravano perdere il segnale durante la sessione di registrazione sono state rimosse da queste analisi(Figura 2-figure supplement 1).10.7554/eLife.21409.003Figure 1.Experimental setup.(A) La scimmia controllava il cursore di un computer su un monitor stereoscopico visto attraverso uno specchio, utilizzando segnali neurali.(B) Ogni sessione di registrazione è iniziata con una breve sessione di calibrazione per costruire il decodificatore. Il decodificatore è stato usato per un blocco di prove 3D (tra 9 e 13 prove per bersaglio), seguito da un blocco di prove 2D (tra 15 e 27 prove per bersaglio). In alcune sessioni, un ulteriore blocco di trial 2D procederà ai blocchi di trial 3D e 2D, oppure un ulteriore blocco di trails 3D seguirà i blocchi di trial 3D e 2D. Abbiamo concentrato le nostre analisi sul primo blocco di prove 3D e sul blocco di prove 2D immediatamente successivo (le caselle grigie). Nei materiali supplementari dimostriamo che i nostri risultati sono invarianti rispetto all’ordine dei blocchi di prova.(C) Posizioni dei 26 obiettivi nel contesto 3D.(D) Posizioni dei 16 obiettivi nel contesto 2D. Gli otto obiettivi comuni al contesto 2D e 3D sono mostrati in rosa. I cerchi rosso, giallo e azzurro rappresentano rispettivamente il piano xy, il piano xz e il piano yz. I dati delle posizioni dei target sono disponibili nella figura 1-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.00310.7554/eLife.21409.004Figure1-source data 1.Target location dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.004
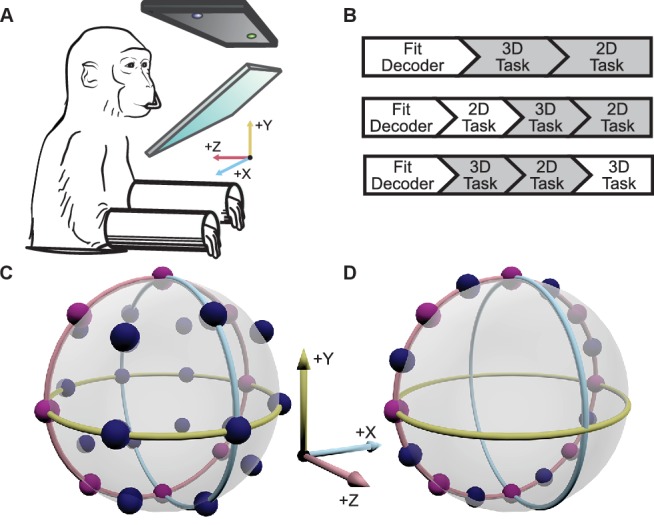
Figura 1 – Dati sorgente 1.1. Impostazione sperimentale;set di dati della posizione del bersaglio;set di dati della posizione del bersaglio.(A) La scimmia controllava il cursore di un computer su un monitor stereoscopico visto attraverso uno specchio, usando segnali neurali.(B) Ogni sessione di registrazione iniziava con una breve sessione di calibrazione per costruire il decodificatore. Il decodificatore è stato usato per un blocco di prove 3D (tra 9 e 13 prove per bersaglio), seguito da un blocco di prove 2D (tra 15 e 27 prove per bersaglio). In alcune sessioni, un ulteriore blocco di trial 2D procederà ai blocchi di trial 3D e 2D, oppure un ulteriore blocco di trails 3D seguirà i blocchi di trial 3D e 2D. Abbiamo concentrato le nostre analisi sul primo blocco di prove 3D e sul blocco di prove 2D immediatamente successivo (le caselle grigie). Nei materiali supplementari dimostriamo che i nostri risultati sono invarianti rispetto all’ordine dei blocchi di prova.(C) Posizioni dei 26 obiettivi nel contesto 3D.(D) Posizioni dei 16 obiettivi nel contesto 2D. Gli otto obiettivi comuni al contesto 2D e 3D sono mostrati in rosa. I cerchi rosso, giallo e azzurro rappresentano rispettivamente il piano xy, il piano xz e il piano yz. I dati delle posizioni dei target sono disponibili nella Figura 1 – dati sorgente 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.00310.7554/eLife.21409.004Figure 1-source data set di dati 1.Target location.DOI:http://dx.doi.org/10.7554/eLife.21409.004DOI:
http://dx.doi.org/10.7554/eLife.21409.004DOI:
http://dx.doi.org/10.7554/eLife.21409.004
I tassi di cottura cambiano in base al contesto
La nostra prima constatazione è che la velocità di sparo durante le corse virtuali dipende dal fatto che il contesto del compito sia 2D o 3D. I tassi di cottura per ogni prova riuscita sono stati calcolati in finestre temporali dalla presentazione dell’obiettivo fino all’acquisizione dell’obiettivo. I tassi sono stati calcolati in media attraverso prove ripetute per ogni obiettivo, per calcolare i tassi di cottura medi di prova. Per l’insieme di obiettivi comuni tra i contesti, abbiamo calcolato le percentuali medie di tiro separatamente per ogni contesto. Nella Figura 2AB, tracciamo i tassi di cottura medi per i target che si trovano nel piano xy per entrambi i contesti. Le linee blu mostrano i tassi di sparo medi di prova dei neuroni a tutti i bersagli del contesto 2D, tracciate in funzione della direzione del bersaglio (azimut). Le linee rosa mostrano la velocità di fuoco media di prova dei neuroni per gli otto bersagli nel piano xy durante il contesto 3D, sempre in funzione dell’azimut. Le linee orizzontali tratteggiate mostrano la media di tiro minima e massima della media di prova tra l’intero set di 26 bersagli nel contesto 3D. Come previsto, le direzioni azimutali preferite sono quasi le stesse tra i due contesti(Figura 2C). I cambiamenti nelle direzioni azimutali preferite sono insignificanti nel test di Moore di campioni accoppiati di angoli per entrambe le scimmie(Moore, 1980; Zar, 2010). Tuttavia, gli intervalli nelle curve di sintonia non sono identici tra i due contesti. Invece, l’intervallo dei tassi di sparo per tutti i 16 bersagli durante il contesto 2D si avvicina, e occasionalmente supera, l’intervallo osservato per tutti i 26 bersagli durante il contesto 3D. Questo risultato è ancora più sorprendente se si considerano i ratei di tiro per l’insieme di otto bersagli che erano identici tra i due contesti. Le unità mostrano una maggiore velocità di fuoco massima e una velocità di fuoco minima inferiore nel contesto 2D rispetto al contesto 3D per il task BCI.10.7554/eLife.21409.005Figure 2.Tuning differences between the 2D and 3D contexts.(A, B) Selected tuning curves for the targets in the xy-plane during the 3D (pink) and 2D (dark blue) contexts from Monkey A (panel A)and Monkey C (panel B). Le velocità di fuoco mostrano la media ± SE per ogni bersaglio. Ci sono state 10 prove per bersaglio nel task 3D per tutte le unità mostrate, ad eccezione dell’ultima unità in(B) dove ci sono state 12 prove per bersaglio. Ci sono state 15 prove per bersaglio nel task 2D per tutte le unità mostrate ad eccezione delle prime due unità in (pannello A) dove ci sono state 27 prove per bersaglio. Le linee orizzontali tratteggiate mostrano la media minima e massima della media di tiro per tutti i 26 bersagli nel contesto 3D.(C) Cambiamenti nella direzione azimutale preferita per Monkey A (in alto) e Monkey C (in basso). I ratei di tiro sono stati usati per adattare i modelli di sintonizzazione log-lineare in modo indipendente per i contesti 2D e 3D per calcolare le direzioni preferite delle unità. La direzione preferita dal contesto 2D è stata confrontata con le componenti x e y della direzione preferita dal contesto 3D per calcolare la variazione della direzione preferita azimutale. I cambiamenti sono insignificanti nel test di Moore di campioni di angoli accoppiati sia per la Scimmia A (R′=0.817, n=471, P>0.1) che per la Scimmia C (R′=0.887, n=409, P>0.05).(D) Istogrammi delle differenze nelle gamme di sintonia per l’insieme di otto obiettivi identici tra i contesti 2D e 3D per Monkey A (in alto) e Monkey C (in basso). Per entrambi i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. In entrambi i soggetti, la gamma dinamica planare 2D era più grande della gamma dinamica planare 3D (Monkey A: ***P≪10-20, test Wilcoxon signed-rank, W=88059, ◊◊◊P<10-18, test del segno, S=334, n=471 unità; Monkey C: **P=0,0032, W=48975, ◊P=0,0134, S=230, n=409 unità).(E) Istogrammi delle differenze nelle gamme di sintonia per l’insieme completo dei bersagli tra il contesto 2D e 3D per Monkey A (in alto) e Monkey C (in basso). L’intervallo di sintonizzazione completo era maggiore nel contesto 2D per la Scimmia A (**P=0,0081, W=63402, ◊P=0,0426, S=258, n=471) e nel contesto 3D per la Scimmia C (***P<10-5, W=31208, ◊P=0,0011, S=171, n=409). I dati per ricreare le curve di sintonia e gli istogrammi sono disponibili in Figura 2 dati fonte 1.DOI:http://dx.doi.org/10.7554/eLife.21409.00510.7554/eLife.21409.006Figure2 dati fonte 1.Esempio di curve di sintonia, direzioni preferite e set di dati dei campi di sintonia.DOI:http://dx.doi.org/10.7554/eLife.21409.00610.7554/eLife.21409.007Figuresupplemento a 2 cifre 1.Unità rimosse dall’analisi a causa della perdita di segnale.(A-E) Cinque unità da Monkey A. (F) Un’unità da Monkey C. Le curve di sintonia dal primo, secondo e terzo blocco di prove sono mostrate come curve da scuro ad arancione chiaro. I ratei di cottura sono disegnati come la media ± SE attraverso le prove nel blocco. I blocchi dal contesto 3D sono disegnati come linee tratteggiate e quelli dal contesto 2D sono disegnati come linee continue. I dati per ricreare questi grafici sono disponibili nella Figura 2-figure supplement 1-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.00710.7554/eLife.21409.008Figure2-figure supplement 1-source data 1.Tuning curves of neurons removed from analysis dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.00810.7554/eLife.21409.009FigureSupplemento a 2 cifre 2.Invarianza delle variazioni dell’intervallo di sintonizzazione.(A) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di target identici nel contesto 2D e 3D quando blocchi di prove 2D precedono blocchi di prove 3D (sinistra) e quando blocchi di prove 3D precedono blocchi di prove 2D (destra). Wl = 178635, ***P<≪10-38, Sl = 477, ◊◊◊P<10-26, nl = 671, Wr = 273191, ***P<10-25, Sr = 564, ◊◊◊P<10-16, nr = 880. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate.(B) Istogrammi che confrontano gli intervalli di sintonia per l’insieme di obiettivi identici in contesti 2D e 3D per tutte le sessioni di registrazione di entrambe le scimmie che hanno usato il decoder PVA (a sinistra) e quelle che hanno usato il decoder OLE (a destra). WPVA = 144603, ***P<10-15, SPVA = 404, ◊◊◊P<10-9, nPVA = 649, WOLE = 20273, ***P<10-10, SOLE = 160, ◊◊◊P<10-8, nOLE = 231.(C) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di obiettivi identici nei contesti 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui la popolazione utilizzata per il controllo BCI era identica tra i due contesti (a sinistra) e quelli in cui la popolazione è cambiata (a destra). Wl = 34298, ***P<10-14, Sl = 212, ◊◊◊P<10-11, nl = 300, Wr = 114164, ***P<10-12, Sr = 352, ◊◊◊P<10-6, nr = 580.(D) Istogrammi che confrontano gli intervalli di sintonia per entrambe le scimmie per l’insieme di obiettivi identici nel contesto 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui il decoder è stato riadattato tra il contesto 3D e 2D (a sinistra) e quelli in cui il decoder era identico alla dimensione z azzerata nel contesto 2D (a destra). Wl = 58688, ***P<10-6, Sl = 251, ◊◊◊P<10-3, nl = 425, Wr = 78290, ***P<10-20, Sr=313, ◊◊◊◊P<10-14, nr = 455. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 2-figure 2 source data data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.00910.7554/eLife.21409.010Figure2-figure supplement 2-figure data 2-fsource data 1.Context order, tipo di decoder, popolazione modificata, e riadattato decoder tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.01010.7554/eLife.21409.011FigureSupplemento a 2 cifre 3.Cambiamenti dell’intervallo di sintonizzazione per Monkey A per una sessione di registrazione.I grafici mostrano le curve di sintonizzazione per i target che giacciono sul piano xy-plane nei contesti 2D (blu scuro) e 3D (rosa). I ratei di sparo sono mostrati come media ± SE (n2D=24; n3D=10). Le velocità medie minime e massime di tiro tra l’insieme di tutti i 26 bersagli del contesto 3D sono disegnate come linee orizzontali tratteggiate. I titoli sopra ogni trama mostrano l’angolo di elevazione, ϕ, che il vettore di direzione preferito dell’unità stimato dai dati 3D fa con il xy-plane . Le unità che hanno mostrato un intervallo di sintonia maggiore tra l’insieme di obiettivi identici nel contesto 2D rispetto al contesto 3D sono contrassegnate con un asterisco rosso nell’angolo in alto a sinistra del grafico. I dati per ricreare questi diagrammi sono disponibili nella Figura 2-figure supplement 3-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.01110.7554/eLife.21409.012Figure2-figure supplement 3-source data 1.Single session tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.01210.7554/eLife.21409.013Figure 2-figure supplement 4.Difference in tuning range in single sessions.(A,B) I grafici mostrano gli istogrammi per gli intervalli di sintonizzazione della differenza per l’insieme di otto target identici tra i contesti 2D e 3D per Monkey A (pannello A) eMonkey C (pannello B) per la singola sessione di registrazione corrispondente ai dati mostrati in Figura 2-figure supplement 3 e una simile singola sessione di registrazione da Monkey C. Per entrambi i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. WA = 333, **P=0,0031, SA = 22, ◊P=0,0037, nA = 28, WC = 731, **P=0,0018, SC = 31, ◊P = 0,0054, nC = 43. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 4-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.01310.7554/eLife.21409.014Figure2-figure supplement 4-source data 1.Single session tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.01410.7554/eLife.21409.015Figuresupplemento a 2 cifre 5.Cambiamenti minimi con contesti ripetuti.(A) I grafici mostrano gli istogrammi della differenza del tuning range tra le ripetizioni del contesto 2D per Monkey A (sinistra) e Monkey C (destra).(B) Le trame mostrano gli istogrammi della differenza di intervallo di sintonia tra le ripetizioni del contesto 3D per la Scimmia A (sinistra) e la Scimmia C (destra). In tutti i grafici, la differenza è calcolata dove i valori positivi rappresentano incrementi del tuning range per il contesto ripetuto rispetto al set di prove iniziale. Per Monkey A, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 2D (contesto 2D: *P=0.0047, W=2233, n.s.P=0.0904, S=47, n=113 unità; contesto 3D: n.s.P=0.1189, W=3829, n.s.P=0.6396, S=60, n=114 unità). Per Monkey C, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 3D (contesto 2D: n.s.P=0,2525, W=3946, n.s.P=0,0829, S=56, n=176 unità; ***P<10-12, W=10952, ◊◊◊P<10-10, S=88, n=291 unità). In particolare, per tutti i casi in cui c’è una differenza significativa tra la ripetizione dello stesso contesto, i mezzi si trovano a sinistra di zero. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi diagrammi sono disponibili in Figura 2-figure supplement 5-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.01510.7554/eLife.21409.016Figure2-figure supplement 5-source data 1.Repeat context tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.016
Per quantificare questo cambiamento, abbiamo calcolato i campi di sintonia planare come la differenza tra il tasso medio di tiro minimo e massimo tra l’insieme di otto obiettivi identici per i due contesti. Abbiamo trovato che 334 di 471 unità su 471 in Monkey A e 230 su 409 unità in Monkey C mostravano un aumento del range di sintonia planare nel contesto 2D rispetto al contesto 3D. L’aumento medio ± errore standard (SE) nel campo di sintonia era di 4,02 ± 0,33 Hz per la Scimmia A e 0,81 ± 0,25 Hz per la Scimmia C (Figura 2D). Il range in frequenza di cottura per un insieme di stimoli identici cambia con il contesto del compito. Ai fini del confronto, le differenze nei range di sintonia per l’insieme di tutti gli obiettivi tra ogni contesto sono mostrate nella Figura 2E.
Nella nostra indagine, abbiamo variato le condizioni sperimentali per analizzare la stabilità dei cambiamenti di sintonia. Mentre la Figura 2D mostra la differenza di sintonia quando il contesto 2D segue il contesto 3D, abbiamo scoperto che simili cambiamenti di sintonia si verificano quando l’ordine è invertito(Figura 2-figure supplement 2A). Abbiamo anche esplorato l’effetto che una scelta diversa nel decoder potrebbe avere sul risultato. Questo è importante, perché il PVA normalizza esplicitamente ogni neurone con la sua profondità di modulazione, mentre l’OLE non lo fa. I risultati sopra riportati sono risultati che comprendono tutte le sessioni di registrazione indipendentemente dai decoder. Quando abbiamo esaminato separatamente le sessioni che utilizzano il decoder PVA o il decoder OLE, abbiamo trovato che i risultati erano individualmente significativi per entrambi i tipi di decoder(Figura 2-figure supplement 2B). Inoltre, in un sottoinsieme delle sessioni di registrazione, l’intera popolazione utilizzata per controllare il movimento del cursore era identica tra i due contesti. Quando abbiamo esaminato la risposta della popolazione da queste sessioni, abbiamo trovato di nuovo cambiamenti simili nel campo di sintonizzazione(Figura 2-figure supplement 2C). Inoltre, per testare gli effetti dell’azzeramento della dimensione z, abbiamo condotto una serie di sessioni di registrazione in cui abbiamo semplicemente riadattato il decoder per il contesto 2D piuttosto che utilizzare il decoder dal contesto 3D con la dimensione z azzerata. Quando abbiamo esaminato separatamente le sessioni che utilizzavano decoder riadattati o identici con la dimensione z azzerata nel contesto 2D, abbiamo trovato che i risultati erano individualmente significativi per entrambi i tipi di sessioni(Figura 2-figure supplement 2D). I cambiamenti negli intervalli di sintonizzazione sono anche evidenti quando si guardano i tassi di cottura da una singola sessione di registrazione da Monkey A(Figura 2-figure supplemento 3). Gli intervalli di sintonizzazione planare 2D e 3D per questa sessione di registrazione e una sessione di registrazione singola simile di Monkey C sono confrontati nella Figura 2-figure supplement 4.
Come mostrato in Figura 1B, c’era un sottoinsieme di sessioni di registrazione in cui un contesto di attività veniva ripetuto dopo il contesto alternativo. Queste sessioni ci hanno permesso di indagare la stabilità degli intervalli di sintonizzazione per contesti identici per tutta la durata di una sessione di registrazione(Figura 2-figure supplement 5). Abbiamo trovato una leggera diminuzione degli intervalli di sintonizzazione per le ripetizioni del contesto 2D per Monkey A e per le ripetizioni del contesto 3D per Monkey C: la seconda presentazione tendeva a diminuire la sintonizzazione rispetto alla prima. Questo può essere dovuto alla stanchezza o alla sazietà. In particolare, questa diminuzione della sintonizzazione sulle presentazioni ripetute è in direzione opposta, come l’aumento della sintonizzazione che osserviamo quando passiamo dal contesto 3D al contesto 2D. Questo suggerisce che i nostri risultati della Figura 2D possono essere una leggera sottostima dell’effettivo aumento della sintonizzazione.
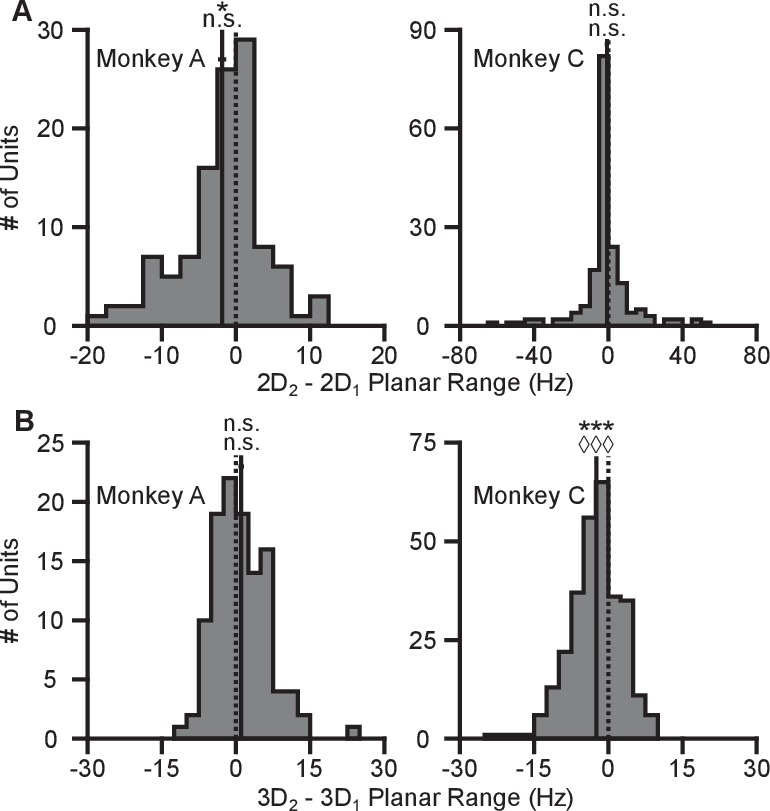
Figura 2-figure supplement 5-source data 1.Esempio di curve di sintonizzazione, direzioni preferite e dataset di intervalli di sintonizzazione.Curve di sintonizzazione, direzioni preferite e dataset di intervalli di sintonizzazione.Unità rimosse dall’analisi a causa della perdita di segnale.Curve di sintonizzazione dei neuroni rimossi dal dataset di analisi.Curve di sintonizzazione dei neuroni rimossi dal dataset di analisi.Invarianza dei cambiamenti dell’intervallo di sintonizzazione.Ordine del contesto, tipo di decodificatore, popolazione modificata e dataset dell’intervallo di sintonizzazione del decodificatore riadattato.Ordine del contesto, tipo di decodificatore, popolazione modificata e dataset dell’intervallo di sintonizzazione del decodificatore riadattato.Ordine del contesto, tipo di decodificatore, popolazione modificata e dataset dell’intervallo di sintonizzazione del decodificatore riadattato.Modifica dell’intervallo di sintonizzazione per la scimmia A per una sessione di registrazione.Modifica dell’intervallo di sintonizzazione per la scimmia A per una sessione di registrazione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.Modifica dell’intervallo di sintonizzazione per una sessione.(A, B) Curve di sintonizzazione selezionate per i target nel xy-plane durante i contesti 3D (rosa) e 2D (blu scuro) da Monkey A (pannello A)e Monkey C (pannello B). Le velocità di fuoco mostrano la media ± SE per ogni bersaglio. Ci sono state 10 prove per bersaglio nel task 3D per tutte le unità mostrate, ad eccezione dell’ultima unità in(B) dove ci sono state 12 prove per bersaglio. Ci sono state 15 prove per bersaglio nel task 2D per tutte le unità mostrate ad eccezione delle prime due unità in (pannello A) dove ci sono state 27 prove per bersaglio. Le linee orizzontali tratteggiate mostrano la media minima e massima della media di tiro per tutti i 26 bersagli nel contesto 3D.(C) Cambiamenti nella direzione azimutale preferita per Monkey A (in alto) e Monkey C (in basso). I ratei di tiro sono stati usati per adattare i modelli di sintonizzazione log-lineare in modo indipendente per i contesti 2D e 3D per calcolare le direzioni preferite delle unità. La direzione preferita dal contesto 2D è stata confrontata con le componenti x e y della direzione preferita dal contesto 3D per calcolare la variazione della direzione preferita azimutale. I cambiamenti sono insignificanti nel test di Moore di campioni di angoli accoppiati sia per la Scimmia A (R′=0.817, n=471, P>0.1) che per la Scimmia C (R′=0.887, n=409, P>0.05).(D) Istogrammi delle differenze nelle gamme di sintonia per l’insieme di otto obiettivi identici tra i contesti 2D e 3D per Monkey A (in alto) e Monkey C (in basso). Per entrambi i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. In entrambi i soggetti, la gamma dinamica planare 2D era più grande della gamma dinamica planare 3D (Monkey A: ***P≪10-20, test Wilcoxon signed-rank, W=88059, ◊◊◊P<10-18, test del segno, S=334, n=471 unità; Monkey C: **P=0,0032, W=48975, ◊P=0,0134, S=230, n=409 unità).(E) Istogrammi delle differenze nelle gamme di sintonia per l’insieme completo dei bersagli tra il contesto 2D e 3D per Monkey A (in alto) e Monkey C (in basso). L’intervallo di sintonizzazione completo era maggiore nel contesto 2D per la Scimmia A (**P=0,0081, W=63402, ◊P=0,0426, S=258, n=471) e nel contesto 3D per la Scimmia C (***P<10-5, W=31208, ◊P=0,0011, S=171, n=409). I dati per ricreare le curve di sintonia e gli istogrammi sono disponibili in Figura 2 dati sorgente 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.00510.7554/eLife.21409.006Cifra dati a 2 fonti 1.Esempio di curve di sintonia, direzioni preferite e set di dati dei campi di sintonia.DOI:http://dx.doi.org/10.7554/eLife.21409.006DOI:
http://dx.doi.org/10.7554/eLife.21409.006DOI:
http://dx.doi.org/10.7554/eLife.21409.006(A-E) Cinque unità da Monkey A. (F) Una unità da Monkey C. Le curve di sintonia dal primo, secondo e terzo blocco di prove sono mostrate come curve da scuro ad arancione chiaro. I ratei di cottura sono disegnati come la media ± SE attraverso le prove nel blocco. I blocchi dal contesto 3D sono disegnati come linee tratteggiate e quelli dal contesto 2D sono disegnati come linee continue. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 1-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.00710.7554/eLife.21409.008Figure 2-figure supplement 1-source data 1.Tuning curves of neurons removed from analysis dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.008DOI:
http://dx.doi.org/10.7554/eLife.21409.008DOI:
http://dx.doi.org/10.7554/eLife.21409.008(A) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di obiettivi identici nei contesti 2D e 3D quando blocchi di prove 2D precedevano blocchi di prove 3D (a sinistra) e quando blocchi di prove 3D precedevano blocchi di prove 2D (a destra). Wl = 178635, ***P<≪10-38, Sl = 477, ◊◊◊P<10-26, nl = 671, Wr = 273191, ***P<10-25, Sr = 564, ◊◊◊P<10-16, nr = 880. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate.(B) Istogrammi che confrontano gli intervalli di sintonia per l’insieme di obiettivi identici in contesti 2D e 3D per tutte le sessioni di registrazione di entrambe le scimmie che hanno usato il decoder PVA (a sinistra) e quelle che hanno usato il decoder OLE (a destra). WPVA = 144603, ***P<10-15, SPVA = 404, ◊◊◊P<10-9, nPVA = 649, WOLE = 20273, ***P<10-10, SOLE = 160, ◊◊◊P<10-8, nOLE = 231.(C) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di obiettivi identici nei contesti 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui la popolazione utilizzata per il controllo BCI era identica tra i due contesti (a sinistra) e quelli in cui la popolazione è cambiata (a destra). Wl = 34298, ***P<10-14, Sl = 212, ◊◊◊P<10-11, nl = 300, Wr = 114164, ***P<10-12, Sr = 352, ◊◊◊P<10-6, nr = 580.(D) Istogrammi che confrontano gli intervalli di sintonia per entrambe le scimmie per l’insieme di obiettivi identici nel contesto 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui il decoder è stato riadattato tra il contesto 3D e 2D (a sinistra) e quelli in cui il decoder era identico alla dimensione z azzerata nel contesto 2D (a destra). Wl = 58688, ***P<10-6, Sl = 251, ◊◊◊P<10-3, nl = 425, Wr = 78290, ***P<10-20, Sr=313, ◊◊◊◊P<10-14, nr = 455. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi diagrammi sono disponibili in Figura 2-figure supplement 2-figure 2 source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.00910.7554/eLife.21409.010Figure 2-figure supplemento 2-figure 2-figure dati sorgente 1.Ordine di contesto, tipo di decodificatore, popolazione cambiata e set di dati del range di sintonia del decodificatore riadattato.DOI:http://dx.doi.org/10.7554/eLife.21409.010DOI:
http://dx.doi.org/10.7554/eLife.21409.010DOI:
http://dx.doi.org/10.7554/eLife.21409.010Le trame mostrano le curve di sintonia per i bersagli che giacciono sul piano xy nei contesti 2D (blu scuro) e 3D (rosa). I ratei di sparo sono indicati come media ± SE (n2D=24; n3D=10). La media minima e massima della velocità di fuoco media tra l’insieme di tutti e 26 i bersagli del contesto 3D sono disegnati come linee orizzontali tratteggiate. I titoli sopra ogni trama mostrano l’angolo di elevazione, ϕ, che il vettore di direzione preferito dell’unità stimato dai dati 3D fa con il xy-plane . Le unità che hanno mostrato un intervallo di sintonia maggiore tra l’insieme di obiettivi identici nel contesto 2D rispetto al contesto 3D sono contrassegnate con un asterisco rosso nell’angolo in alto a sinistra del grafico. I dati per ricreare questi diagrammi sono disponibili nella figura 2-figure supplement 3-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.01110.7554/eLife.21409.012Figure 2-figure supplement 3-source data set di dati 1.Single session tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.012DOI:
http://dx.doi.org/10.7554/eLife.21409.012DOI:
http://dx.doi.org/10.7554/eLife.21409.012(A,B) I grafici mostrano gli istogrammi per gli intervalli di sintonizzazione delle differenze per l’insieme di otto target identici tra i contesti 2D e 3D per Monkey A (pannello A)e Monkey C (pannello B) per la singola sessione di registrazione corrispondente ai dati mostrati in Figura 2-figure supplement 3 e una simile singola sessione di registrazione da Monkey C. Per entrambi i pannelli: linee verticali solide, mezzi di distribuzione; linee orizzontali solide, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due intervalli di sintonia. WA = 333, **P=0,0031, SA = 22, ◊P=0,0037, nA = 28, WC = 731, **P=0,0018, SC = 31, ◊P = 0,0054, nC = 43. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 4-source data 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.01310.7554/eLife.21409.014Figure 2-figure supplement 4-source data set di dati 1.Single session tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.014DOI:
http://dx.doi.org/10.7554/eLife.21409.014DOI:
http://dx.doi.org/10.7554/eLife.21409.014(A) Le trame mostrano gli istogrammi della differenza del campo di sintonia tra le ripetizioni del contesto 2D per Monkey A (sinistra) e Monkey C (destra).(B) Le trame mostrano gli istogrammi della differenza del campo di sintonia tra le ripetizioni del contesto 3D per la Scimmia A (sinistra) e la Scimmia C (destra). In tutti i grafici, la differenza è calcolata dove i valori positivi rappresentano incrementi del tuning range per il contesto ripetuto rispetto alla serie iniziale di prove. Per Monkey A, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 2D (contesto 2D: *P=0.0047, W=2233, n.s.P=0.0904, S=47, n=113 unità; contesto 3D: n.s.P=0.1189, W=3829, n.s.P=0.6396, S=60, n=114 unità). Per Monkey C, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 3D (contesto 2D: n.s.P=0,2525, W=3946, n.s.P=0,0829, S=56, n=176 unità; ***P<10-12, W=10952, ◊◊◊P<10-10, S=88, n=291 unità). In particolare, per tutti i casi in cui c’è una differenza significativa tra la ripetizione dello stesso contesto, i mezzi si trovano a sinistra di zero. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi diagrammi sono disponibili in Figura 2-figure supplement 5-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.01510.7554/eLife.21409.016Figure 2-figure supplement 5-source data set di dati 1.Repeat context tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.016DOI:
http://dx.doi.org/10.7554/eLife.21409.016DOI:
http://dx.doi.org/10.7554/eLife.21409.016
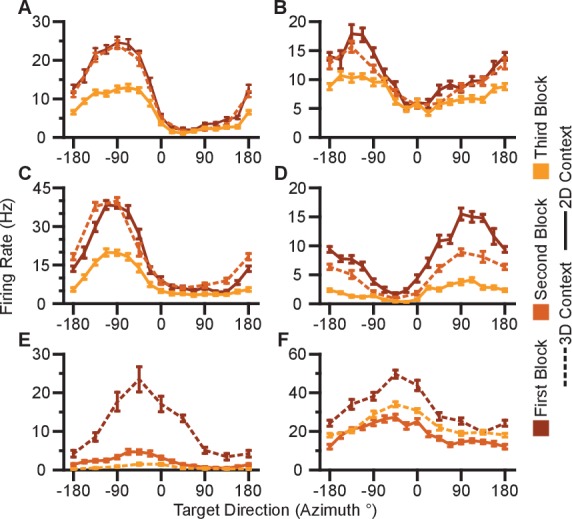
Figura 2-figure supplement 1-source data 1.Unità rimosse dall’analisi a causa della perdita di segnale.curve di sintonia dei neuroni rimossi dall’insieme di dati di analisi.curve di sintonia dei neuroni rimossi dall’insieme di dati di analisi.(A-E) Cinque unità da Monkey A. (F) Una unità da Monkey C. Le curve di sintonia dal primo, secondo e terzo blocco di prove sono mostrate come curve da scuro ad arancione chiaro. I ratei di cottura sono disegnati come la media ± SE attraverso le prove nel blocco. I blocchi dal contesto 3D sono disegnati come linee tratteggiate e quelli dal contesto 2D sono disegnati come linee continue. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 1-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.00710.7554/eLife.21409.008Figure 2-figure supplement 1-source data 1.Tuning curves of neurons removed from analysis dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.008DOI:
http://dx.doi.org/10.7554/eLife.21409.008DOI:
http://dx.doi.org/10.7554/eLife.21409.008
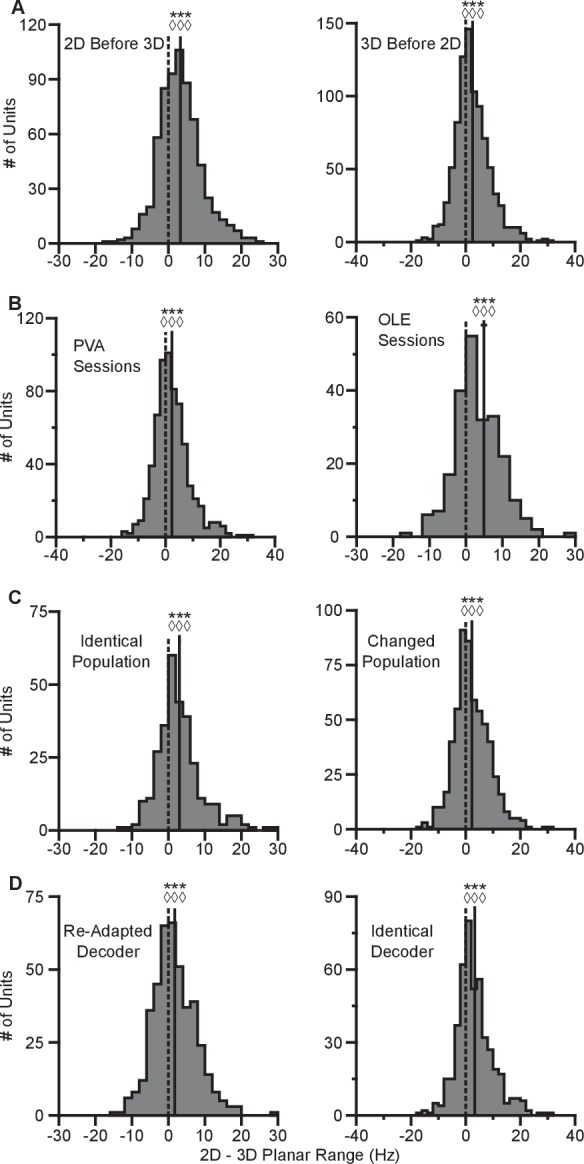
Figura 2-figure supplemento 2-figure dati fonte 1.Ordine di contesto, tipo di decodificatore, popolazione modificata e set di dati dell’intervallo di sintonizzazione del decodificatore riadattati.ordine di contesto, tipo di decodificatore, popolazione modificata e set di dati dell’intervallo di sintonizzazione del decodificatore riadattati.(A) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di obiettivi identici nel contesto 2D e 3D quando blocchi di prove 2D precedono blocchi di prove 3D (sinistra) e quando blocchi di prove 3D precedono blocchi di prove 2D (destra). Wl = 178635, ***P<≪10-38, Sl = 477, ◊◊◊P<10-26, nl = 671, Wr = 273191, ***P<10-25, Sr = 564, ◊◊◊P<10-16, nr = 880. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate.(B) Istogrammi che confrontano gli intervalli di sintonia per l’insieme di obiettivi identici in contesti 2D e 3D per tutte le sessioni di registrazione di entrambe le scimmie che hanno usato il decoder PVA (a sinistra) e quelle che hanno usato il decoder OLE (a destra). WPVA = 144603, ***P<10-15, SPVA = 404, ◊◊◊P<10-9, nPVA = 649, WOLE = 20273, ***P<10-10, SOLE = 160, ◊◊◊P<10-8, nOLE = 231.(C) Istogrammi che confrontano gli intervalli di sintonizzazione di entrambe le scimmie per l’insieme di obiettivi identici nei contesti 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui la popolazione utilizzata per il controllo BCI era identica tra i due contesti (a sinistra) e quelli in cui la popolazione è cambiata (a destra). Wl = 34298, ***P<10-14, Sl = 212, ◊◊◊P<10-11, nl = 300, Wr = 114164, ***P<10-12, Sr = 352, ◊◊◊P<10-6, nr = 580.(D) Istogrammi che confrontano gli intervalli di sintonia per entrambe le scimmie per l’insieme di obiettivi identici nel contesto 2D e 3D per il sottoinsieme delle sessioni di registrazione in cui il decoder è stato riadattato tra il contesto 3D e 2D (a sinistra) e quelli in cui il decoder era identico alla dimensione z azzerata nel contesto 2D (a destra). Wl = 58688, ***P<10-6, Sl = 251, ◊◊◊P<10-3, nl = 425, Wr = 78290, ***P<10-20, Sr=313, ◊◊◊◊P<10-14, nr = 455. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi diagrammi sono disponibili in Figura 2-figure supplement 2-figure 2 source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.00910.7554/eLife.21409.010Figure 2-figure supplemento 2-figure 2-figure dati sorgente 1.Ordine di contesto, tipo di decodificatore, popolazione cambiata e set di dati del range di sintonia del decodificatore riadattato.DOI:http://dx.doi.org/10.7554/eLife.21409.010DOI:
http://dx.doi.org/10.7554/eLife.21409.010DOI:
http://dx.doi.org/10.7554/eLife.21409.010
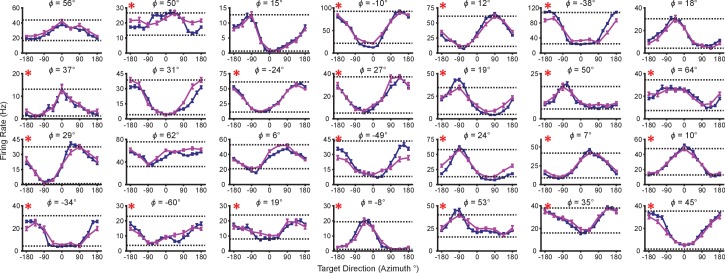
Figura 2-figure supplement 3-source data 1.L’intervallo di sintonizzazione cambia per la scimmia A per una sessione di registrazione.dataset delle curve di sintonia di una singola sessione.dataset delle curve di sintonia di una singola sessione.I grafici mostrano le curve di sintonia per i target che giacciono sul piano xy nei contesti 2D (blu scuro) e 3D (rosa). I tassi di sparo sono mostrati come media ± SE (n2D=24; n3D=10). La media minima e massima della velocità di fuoco media tra l’insieme di tutti e 26 i bersagli del contesto 3D sono disegnati come linee orizzontali tratteggiate. I titoli sopra ogni trama mostrano l’angolo di elevazione, ϕ, che il vettore di direzione preferito dell’unità stimato dai dati 3D fa con il xy-plane . Le unità che hanno mostrato un intervallo di sintonia maggiore tra l’insieme di obiettivi identici nel contesto 2D rispetto al contesto 3D sono contrassegnate con un asterisco rosso nell’angolo in alto a sinistra del grafico. I dati per ricreare questi diagrammi sono disponibili nella figura 2-figure supplement 3-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.01110.7554/eLife.21409.012Figure 2-figure supplement 3-source data set di dati 1.Single session tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.012DOI:
http://dx.doi.org/10.7554/eLife.21409.012DOI:
http://dx.doi.org/10.7554/eLife.21409.012
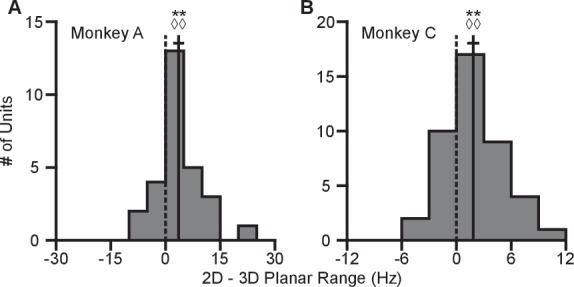
Figura 2-figure supplement 4-source data 1.Differenza negli intervalli di sintonizzazione in singole sessioni.dataset dell’intervallo di sintonizzazione di una singola sessione.dataset dell’intervallo di sintonizzazione di una singola sessione.(A,B) I grafici mostrano gli istogrammi per gli intervalli di sintonizzazione della differenza per l’insieme di otto target identici tra i contesti 2D e 3D per Monkey A (pannello A)e Monkey C (pannello B) per la singola sessione di registrazione corrispondente ai dati mostrati in Figura 2-figure supplement 3 e una sessione di registrazione singola simile da Monkey C. Per entrambi i pannelli: linee verticali solide, mezzi di distribuzione; linee orizzontali solide, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due intervalli di sintonizzazione. WA = 333, **P=0,0031, SA = 22, ◊P=0,0037, nA = 28, WC = 731, **P=0,0018, SC = 31, ◊P = 0,0054, nC = 43. W, Wilcoxon signed-rank test, S, sign test, n, numero di unità analizzate. I dati per ricreare questi grafici sono disponibili in Figura 2-figure supplement 4-source data 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.01310.7554/eLife.21409.014Figure 2-figure supplement 4-source data set di dati 1.Single session tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.014DOI:
http://dx.doi.org/10.7554/eLife.21409.014DOI:
http://dx.doi.org/10.7554/eLife.21409.014

Figura 2-figure supplement 5-source data 1.2. Cambiamenti minimi con contesti ripetuti;Ripetizione dell’insieme di dati dell’intervallo di sintonizzazione del contesto;Ripetizione dell’insieme di dati dell’intervallo di sintonizzazione del contesto.(A) I grafici mostrano gli istogrammi della differenza del tuning range tra le ripetizioni del contesto 2D per Monkey A (sinistra) e Monkey C (destra).(B) Le trame mostrano gli istogrammi della differenza del range di sintonia tra le ripetizioni del contesto 3D per la Scimmia A (sinistra) e la Scimmia C (destra). In tutti i grafici, la differenza è calcolata dove i valori positivi rappresentano incrementi del tuning range per il contesto ripetuto rispetto al set di prove iniziale. Per Monkey A, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 2D (contesto 2D: *P=0.0047, W=2233, n.s.P=0.0904, S=47, n=113 unità; contesto 3D: n.s.P=0.1189, W=3829, n.s.P=0.6396, S=60, n=114 unità). Per Monkey C, c’è una differenza significativa negli intervalli di sintonizzazione tra le ripetizioni del contesto 3D (contesto 2D: n.s.P=0,2525, W=3946, n.s.P=0,0829, S=56, n=176 unità; ***P<10-12, W=10952, ◊◊◊P<10-10, S=88, n=291 unità). In particolare, per tutti i casi in cui c’è una differenza significativa tra la ripetizione dello stesso contesto, i mezzi si trovano a sinistra di zero. Per tutti i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto di uguaglianza tra i due campi di sintonia. I dati per ricreare questi diagrammi sono disponibili in Figura 2-figure supplement 5-source data 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.01510.7554/eLife.21409.016Figure 2-figure supplement 5-source data set di dati 1.Repeat context tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.016DOI:
http://dx.doi.org/10.7554/eLife.21409.016DOI:
http://dx.doi.org/10.7554/eLife.21409.016
Gli aumenti del campo di sintonizzazione sono guidati dall’adattamento del campo dinamico
Abbiamo poi indagato su diversi meccanismi che potrebbero essere alla base delle variazioni del tasso di tiro in funzione del contesto che abbiamo osservato durante il compito della BCI. Abbiamo considerato tre possibili meccanismi: (1) un meccanismo di ri-orientamento, in cui i soggetti mirano a punti diversi dai bersagli(Jarosiewicz et al., 2008; Chase et al., 2010), (2) un meccanismo di guadagno di velocità, in cui i soggetti cambiano la velocità prevista tra i due contesti(Moran e Schwartz, 1999), e (3) un meccanismo di adattamento della gamma dinamica, in cui le unità si adattano per utilizzare la loro gamma dinamica disponibile in entrambi i contesti(Brenner et al., 2000). Queste strategie fanno ciascuna previsioni diverse su come i cambiamenti di sintonia si correleranno tra le popolazioni di cellule registrate simultaneamente. Qui di seguito discutiamo ciascuno di questi meccanismi a turno.
Meccanismo di ri-orientamento
Questo meccanismo si riferisce al processo di puntare a un target virtuale piuttosto che a quello presentato(Jarosiewicz et al., 2008; Chase et al., 2010). Sotto il re-aimpiego, si suppone che le curve di sintonia rimangano fisse, ma i tassi di sparo su obiettivi identici possono cambiare se i loro punti di reimpiego sono diversi nei vari contesti. I processi di ri-puntatura sono stati trovati per spiegare la maggior parte dell’adattamento a breve termine alle rotazioni visuo-motorie sperimentate sotto il controllo di BCI(Chase et al., 2012). Perché il ri-orientamento può avvenire tra il contesto 3D e quello 2D? Nel contesto 3D, il reimpostamento della mira comporterebbe probabilmente un movimento del cursore lontano dal bersaglio, e quindi non sarebbe vantaggioso. Nel contesto 2D, invece, puntare punti in qualsiasi punto della dimensione z che mantengono una proiezione costante nel piano xy comporterebbe un movimento rettilineo. Se le direzioni preferite della popolazione sono distribuite in modo uniforme, non ci sarebbe alcun beneficio in termini di velocità, sia ‘spingendo’ o ‘tirando’ mentalmente il cursore sopra o sotto il piano z durante il compito 2D: l’aumento dei tassi di sparo per la popolazione di neuroni su un lato del piano sarebbe bilanciato da una diminuzione dei tassi di sparo per la popolazione di neuroni sull’altro lato del piano in modo che la velocità rimanga costante. Tuttavia, se ci sono distorsioni nelle distribuzioni delle direzioni preferite in profondità, il ri-orientamento in profondità potrebbe aumentare i ratei di fuoco più di quanto non diminuiscano, permettendo al soggetto di spingere il cursore più velocemente verso il bersaglio visualizzato. Con questo meccanismo, le unità subirebbero un aumento o una diminuzione del campo di sintonia, a seconda dell’elevazione della direzione preferita dell’unità rispetto all’elevazione del punto di mira.
Illustriamo questi cambiamenti dipendenti dalla sintonizzazione per uno scenario di esempio nella Figura 3A. Il colore sulla sfera indica il cambiamento relativo del campo di sintonia per un’unità con una direzione preferita in quel punto. Le direzioni preferite di tre unità di esempio sono mostrate come punti di colore verde chiaro sulla sfera. Sebbene le tre unità abbiano quasi le stesse direzioni azimutali preferite (vicino a 45∘), l’angolo di elevazione dei vettori di direzione preferiti è positivo per le prime due unità e negativo per la terza. Sotto il meccanismo di ri-orientamento, il punto di ri-orientamento per il bersaglio con una direzione azimutale di 45∘ nel contesto 2D sarebbe sopra quel bersaglio, più vicino alle direzioni preferite delle prime due unità e più lontano dalla direzione preferita della terza unità. Il punto di ri-orientamento si troverebbe sopra il piano xy a causa della polarizzazione nella distribuzione delle tre unità. Con questo punto di mira, le prime due unità avrebbero una velocità di fuoco maggiore e la terza unità diminuirebbe la sua velocità di fuoco nel contesto 2D fino al bersaglio con una direzione azimutale di 45∘. L’aumento di tiro delle due unità supererebbe la diminuzione del rateo di tiro della terza unità, spingendo successivamente il cursore verso il bersaglio più velocemente. Le curve di sintonia di queste tre unità per i contesti 3D e 2D sotto il meccanismo di riposizionamento sono disegnate sotto la sfera di riposizionamento. In questo esempio ipotetico, le prime due unità mostrano un campo di sintonia aumentato nel contesto 2D, mentre la terza unità mostra un campo di sintonia diminuito.10.7554/eLife.21409.017Figure 3.Hypotheses for tuning changes.(A) Illustrazione dell’ipotesi di strategia di ri-orientamento.(B) Illustrazione dell’ipotesi di velocità. (C) Illustrazione dell’ipotesi di adattamento della gamma dinamica. Per ogni ipotesi, la prima riga mostra le mappe di calore della variazione relativa del campo di sintonia in funzione della direzione preferita. A scopo illustrativo, la mappa di calore in (pannello A) è mostrata come 2D Range – 3D Planar Range3D Range e scalata nel range [-0.25,0.25]. Le altre mappe di calore sono mostrate come 1-3D Planar Range2D Range e scalate nel range [-1,1]. Le tre righe in basso mostrano i cambiamenti di esempio nelle funzioni di sintonizzazione per tre unità con le direzioni preferite disegnate come punti verdi chiari sulle mappe di calore.DOI:http://dx.doi.org/10.7554/eLife.21409.017
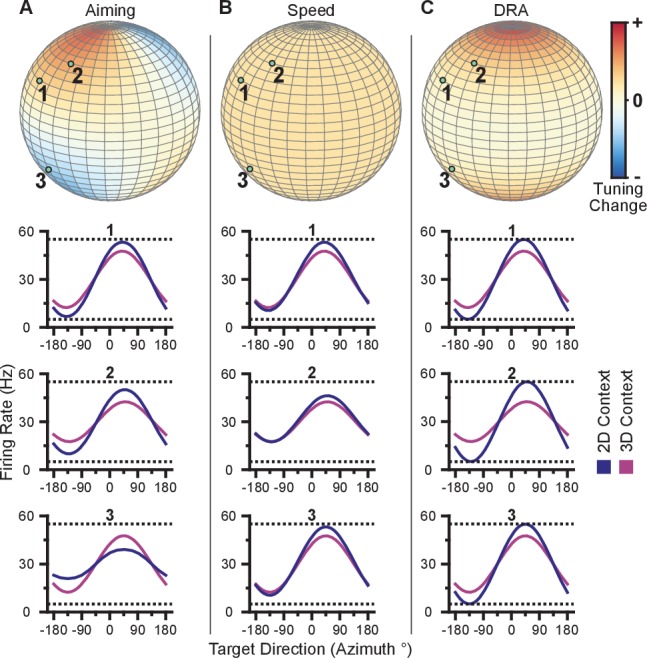
Figura 3.Ipotesi per i cambiamenti di sintonia.(A) Illustrazione dell’ipotesi di strategia di ri-orientamento.(B) Illustrazione dell’ipotesi della velocità. (C) Illustrazione dell’ipotesi di adattamento della gamma dinamica. Per ogni ipotesi, la prima riga mostra le mappe di calore della variazione relativa del campo di sintonia in funzione della direzione preferita. A scopo illustrativo, la mappa di calore in (pannello A) è mostrata come 2D Range – 3D Planar Range3D Range e scalata nel range [-0.25,0.25]. Le altre mappe di calore sono mostrate come 1-3D Planar Range2D Range e scalate nel range [-1,1]. Le tre righe in basso mostrano i cambiamenti di esempio nelle funzioni di sintonizzazione per tre unità con le direzioni preferite disegnate come punti verdi chiari sulle mappe di calore.DOI:
http://dx.doi.org/10.7554/eLife.21409.017
Meccanismo di guadagno della velocità
Questo meccanismo si riferisce al processo di codifica di velocità diverse nelle velocità di cottura tra i due contesti. Moran e Schwartz hanno dimostrato che la velocità di movimento può avere effetti sia additivi che moltiplicativi sulla velocità di cottura dei singoli neuroni(Moran e Schwartz, 1999). Essi hanno modellato la relazione tra la velocità di movimento, 𝐯, e la velocità di sparo neurale, ri, con la seguente equazione:(1)ri=b0,i+|||𝐯||bs,i+mi𝐯⋅𝐩i
dove ||||𝐯|| è la velocità di movimento e bs,i scala l’effetto additivo della velocità. A differenza del tradizionale modello di sintonia lineare(Georgopoulos et al., 1982), la profondità di modulazione, mi, scala non solo gli effetti di sintonia direzionale ma anche l’effetto moltiplicativo della velocità. Gli algoritmi di decodifica utilizzati in questi studi convertono le velocità di scatto della popolazione in velocità del cursore. Una descrizione più dettagliata degli algoritmi di decodifica è fornita nella sezione Materiali e metodi. In breve, tassi di cottura più estremi (cioè tassi di cottura molto bassi e alti rispetto alla linea di base) aumenterebbero la velocità del cursore. Così, l’aumento della velocità prevista del cursore durante il contesto 2D aumenterebbe il campo di sintonia delle unità. Illustriamo la variazione relativa del campo di sintonia in funzione della direzione preferita prevista da una variazione della velocità prevista in Figura 3B. A differenza del meccanismo di ri-orientamento, il cambiamento relativo del campo di sintonizzazione previsto non varia con la direzione preferita. Invece, la variazione relativa del campo di sintonia è identica per tutte le unità. Seguendo l’equazione 1, il campo di sintonia per un’unità, ρi, è la differenza tra il rateo di tiro massimo e minimo, ri, nell’intervallo dei bersagli, 𝐝, nel xy-plane . Poiché l’intervallo di sintonia è la differenza tra i tassi tra i bersagli, l’effetto additivo annulla e solo gli effetti moltiplicativi della velocità rimangono nell’intervallo di sintonia, ρi=2mi||𝐯|||cos(ϕi). Quindi, se la velocità prevista durante il contesto 2D è maggiore del 20% rispetto a quella del contesto 3D, il campo di sintonia 2D sarà maggiore del 20% rispetto al campo di sintonia planare 3D.
Meccanismo di adattamento della gamma dinamica
Questo meccanismo si riferisce al processo delle unità che regolano le loro curve di sintonia per utilizzare il loro campo di sintonia completo nel contesto del compito dato. Questo processo è simile all’adattamento del campo dinamico osservato nelle cortecce sensoriali, dove i neuroni regolano le loro funzioni di sintonizzazione per codificare in modo ottimale il campo degli stimoli in ingresso. Nel contesto 2D, la dimensione z non è più rilevante. Successivamente, la porzione del campo di sintonizzazione 3D assegnata alla codifica della dimensione z può essere utilizzata per codificare i target nel piano xy durante il contesto 2D. Illustriamo il relativo cambiamento del campo di sintonia in funzione della direzione preferita prevista dall’adattamento del campo dinamico in Figura 3C. A differenza di una variazione della velocità prevista, la variazione relativa del campo di sintonia prevista a causa dell’adattamento del campo dinamico varia con l’angolo di elevazione, ϕ, della direzione preferita. Con l’adattamento della gamma dinamica, la gamma di sintonia 2D sarebbe uguale alla gamma di sintonia completa (2mi dall’equazione 1), mentre la gamma di sintonia planare 3D è scalata dal coseno dell’angolo di elevazione, 2micos(ϕi). Ci riferiamo a questo come effetto “dose-risposta”. L’aumento della ‘dose’ dell’angolo di elevazione porta ad un aumento della risposta della variazione del range di sintonia.
Troviamo che i nostri dati siano più coerenti con il meccanismo di adattamento della gamma dinamica. Due prove lo suggeriscono. In primo luogo, i nostri dati mostrano l’effetto dose-risposta previsto solo dall’adattamento della gamma dinamica. In secondo luogo, non troviamo alcuna prova di cambiamenti coordinati e opposti nella gamma dinamica per i neuroni le cui direzioni preferite 3D sono state riflesse attraverso il piano xy, come previsto dal meccanismo di ri-orientamento. Spieghiamo queste analisi per esteso qui di seguito.
Per indagare se i dati mostrano un effetto dose-risposta, abbiamo tracciato il rapporto tra i campi planari 3D e 2D rispetto al valore assoluto dell’angolo di elevazione(Figura 4A,B). Quando abbiamo inserito una regressione lineare ponderata a questi dati, abbiamo trovato pendenze significative e negative, che indicano che i neuroni sintonizzati su angoli di elevazione più grandi mostrano variazioni più ampie della gamma dinamica tra 2D e 3D (Monkey A: P<10-12, F-test; Monkey C, P=0.00125). In particolare, il rapporto dei campi di sintonizzazione dovrebbe seguire una relazione coseno-coseno con l’angolo di elevazione piuttosto che lineare. Tuttavia, quando abbiamo ripetuto questa analisi utilizzando il coseno dell’angolo di elevazione piuttosto che il valore assoluto, i risultati non sono cambiati(Figura 4-figure supplement 1A). Questi risultati sono previsti solo dall’ipotesi di adattamento del campo dinamico: le unità sembrano aumentare il loro campo di modulazione per includere la porzione di campo di sintonia che ha codificato e controllato la dimensione z nel contesto 3D. Così, questo cambia il loro contributo alla codifica e al controllo delle dimensioni x e y rilevanti nel contesto 2D del compito BCI. Quando abbiamo confrontato i campi di sintonizzazione completi del contesto 2D e 3D, abbiamo scoperto che più della metà delle unità (54,8%) aveva un campo di sintonizzazione completo in 2D maggiore rispetto al 3D per la Scimmia A, mentre meno della metà delle unità (41,8%) aveva un campo di sintonizzazione completo in 2D maggiore rispetto al 3D per la Scimmia C(Figura 2E).10.7554/eLife.21409.018Figure 4.Evidence for dynamic range adaptation.(A) Dose-response effects in the tuning changes for Monkey A. (B) Dose-response effects in the tuning changes for Monkey C. The ratio of 3D planar to 2D dynamic ranges are plotted against the absolute value of the elevation angle (ϕ) of the PD vectors. Gli adattamenti lineari ponderati per i punti dei dati sono mostrati in nero. Gli accoppiamenti hanno pendenze negative. bA=-0,0033, FA=53,9, P<10-12, nA=471, bC=-0,0015, FC=10,6, P=0,00125, nC=409. b, pendenza, F, F-test rispetto al modello costante, n, numero di unità analizzate. L’oscurità dei punti corrisponde ai pesi utilizzati per la lineare si adatta alla legenda mostrata a destra. Per fornire il contrasto, la soglia superiore di colormap per i pesi è stata fissata a 40. Le curve di sintonia per i due punti che si trovano significativamente al di fuori della linea di tendenza in(B) sono mostrate in Figura 4-figure supplement 1B.(C,D) Tassi di sparamento dalla Scimmia A per le prime due unità della Figura 2A. Entrambe le unità hanno una PD azimutale vicino a -135∘. Le prime tre barre mostrano i ratei di tiro nel contesto 3D per il bersaglio che giaceva a -135∘ sul xy-plane (rosa) e i due bersagli immediatamente sopra (rosa scuro), e sotto (rosa chiaro) quel bersaglio (E). La velocità di sparo nel contesto 2D al bersaglio a -135∘ è mostrata nella quarta barra (F). L’unità 1 aveva una direzione preferita sotto il piano xy(U1;Z=61, **P=0.001). L’unità 2 aveva una direzione preferita sopra il piano xy(U2;Z=154, ***P<10-3). Nonostante questa differenza, entrambe le unità hanno mostrato un aumento della velocità di fuoco verso il bersaglio planare nel contesto 2D rispetto al contesto 3D (U1;2D,3D=114, **P=0.0098, U2;2D,3D=126, *P=0.0299).(G,H) Insieme simile di velocità di tiro da Monkey C per le prime due unità della Figura 2B. I bersagli corrispondenti sono mostrati in(I e J). Entrambe le unità avevano un PD azimutale vicino a -45∘. L’unità 1 aveva una direzione preferita sotto il xy-plane U1;Z=69, ***P<10-3). L’unità 2 aveva una direzione preferenziale sopra il piano xy(U2;Z=164, **P=0.0028). Nonostante questa differenza, entrambe le unità hanno mostrato un aumento della velocità di fuoco verso il bersaglio planare nel contesto 2D rispetto al contesto 3D (U1;2D,3D=89, *P=0,0165, U2;2D,3D=95, *P=0,0374). Le velocità di sparo sono tracciate come media ± SE (U, prove U di Mann-Whitney, n2D e n3D sono le stesse della Figura 2A,B). I dati per ricreare questi grafici sono disponibili nella Figura 4 dati fonte 1.DOI:http://dx.doi.org/10.7554/eLife.21409.01810.7554/eLife.21409.019Figuredati fonte 1.Cambiamento del range di sintonia rispetto agli angoli di elevazione e al set di dati dei cambiamenti neuronali accoppiati.DOI:http://dx.doi.org/10.7554/eLife.21409.01910.7554/eLife.21409.020Figure4-figure supplement 1.Dose-response effects in sparing rate changes.(A) Gli effetti dose-response nei cambiamenti di tuning sono mostrati per Monkey A (sinistra) e Monkey C (destra). Il rapporto tra le gamme dinamiche 3D planari e 2D viene tracciato contro il coseno dell’angolo di elevazione (ϕ) dei vettori PD. Gli adattamenti lineari ponderati per i punti dei dati sono mostrati in nero. Gli accoppiamenti hanno pendenze positive. bA=0,397, FA=63,6, P<10-13, nA=471, bC=0,152, FC=8,92, P=0,00299, nC=409.b, pendenza, F, F-test rispetto al modello costante, n, numero di unità analizzate. L’oscurità dei punti corrisponde ai pesi utilizzati per la lineare si adatta alla legenda mostrata a destra. Per fornire il contrasto, la soglia superiore di colormap per i pesi è stata fissata a 40.(B) Le curve di sintonia per i due punti che si trovano significativamente al di fuori della linea di tendenza per la Scimmia C. I grafici mostrano le curve di sintonia per i bersagli che giacciono sul piano xy nei contesti 2D (linea continua) e 3D (linea tratteggiata). I ratei di sparo sono indicati come media ± SE. I tassi di tiro medi minimi e massimi tra l’insieme di tutti i 26 bersagli del contesto 3D sono disegnati come linee orizzontali tratteggiate. Le curve di sintonia e le linee minime e massime sono colorate (da scuro ad arancione chiaro) secondo l’ordine di blocco dei dati (dal primo al terzo blocco). Le curve di sintonia mostrano una risposta rumorosa ai target nel piano xy con intervalli stimati ridotti nel contesto 2D. I dati per ricreare questi grafici sono disponibili nella Figura 4-figure supplement 1-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.02010.7554/eLife.21409.021Figure4-figure supplement 1-source data 1.Tuning range change versus elevation angle and outlier neural tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.021
Abbiamo anche cercato prove di cambiamenti coordinati e opposti nella gamma dinamica per scenari come le Unità 1 e 3 illustrate nella Figura 3A, in cui una coppia di unità con direzioni preferenziali 2D quasi identiche aveva direzioni preferenziali 3D che si specchiavano sul piano xy. Come spiegato sopra, la strategia di ri-orientamento prevede che una unità mostrerebbe un aumento del rateo di tiro al bersaglio planare nel contesto 2D rispetto al contesto 3D, mentre l’altra unità mostrerebbe un rateo di tiro ridotto. Nelle ipotesi alternative, entrambe le unità mostrerebbero un aumento della velocità di fuoco al bersaglio planare nel contesto 2D. I risultati di una coppia di unità corrispondenti a questo scenario sono mostrati per Monkey A(Figura 4C,D) e Monkey C(Figura 4G,H). L’attività per queste coppie di unità di esempio non è coerente con la strategia di ri-orientamento. Entrambe le unità dimostrano la massima velocità di tiro al bersaglio planare nel contesto 2D. Per studiare se i risultati erano coerenti con la strategia di mira a livello di popolazione, abbiamo sviluppato un algoritmo per prevedere i punti di mira ottimali per la popolazione nel contesto 2D, basato sui tassi di tiro nel contesto 3D. Questo algoritmo ci permette di prevedere quali neuroni mostrerebbero aumenti della gamma dinamica sotto il meccanismo di ri-orientamento e quali neuroni mostrerebbero diminuzioni della gamma dinamica. Si noti che sia sotto il meccanismo di guadagno di velocità che sotto il meccanismo di adattamento della gamma dinamica, non si prevede che i neuroni mostrino diminuzioni della loro gamma dinamica. Abbiamo applicato questa analisi alle sessioni di registrazione in cui l’intera popolazione era identica tra i due contesti. Per la Scimmia A, delle 87 unità previste per aumentare il range di sintonia, 66 sono state osservate aumentare. Delle 55 unità che si prevedeva diminuissero il range di sintonizzazione, solo otto sono state osservate per farlo. Per la Scimmia C, delle 86 unità che si prevede aumentino il campo di sintonizzazione, 57 sono state osservate aumentare. Delle 72 unità che si prevedeva diminuissero il campo di sintonizzazione, solo 30 sono state osservate in questo senso. In entrambe le scimmie, più della metà dei neuroni che si prevedeva mostrassero diminuzioni della gamma dinamica dal contesto 3D al 2D sotto il meccanismo di ri-orientamento, hanno effettivamente mostrato aumenti della gamma dinamica, come previsto dal meccanismo di adattamento della gamma dinamica.
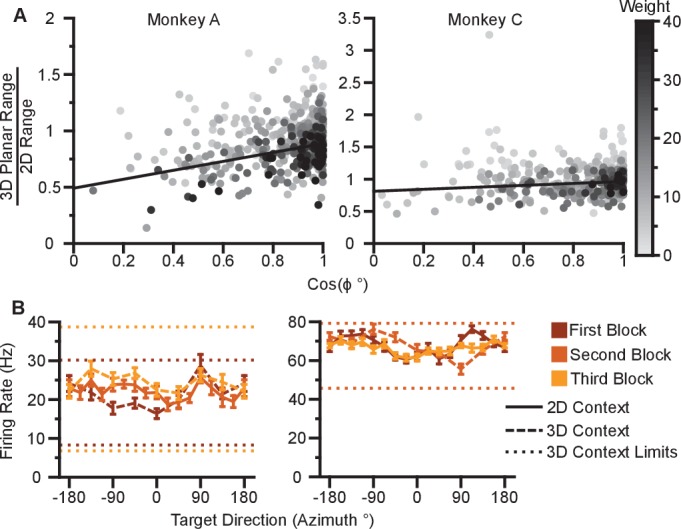
Figura 4-figure supplement 1-source data 1.Figura 4—supplemento alla figura 1—dati sorgente 1. Prove per l’adattamento della gamma dinamica.modifica della gamma di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale accoppiate.modifica della gamma di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale accoppiate.modifica della gamma di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale accoppiate.modifica della gamma di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale accoppiate.dataset di curve di sintonizzazione neurale accoppiate.(A) Effetti dose-risposta nei cambiamenti di sintonia per Monkey A.(B) Effetti dose-risposta nei cambiamenti di sintonia per Monkey C. Il rapporto tra i campi dinamici planari 3D e 2D è tracciato rispetto al valore assoluto dell’angolo di elevazione (ϕ) dei vettori PD. Gli adattamenti lineari ponderati per i punti dei dati sono mostrati in nero. Gli accoppiamenti hanno pendenze negative. bA=-0,0033, FA=53,9, P<10-12, nA=471, bC=-0,0015, FC=10,6, P=0,00125, nC=409. b, pendenza, F, F-test rispetto al modello costante, n, numero di unità analizzate. L’oscurità dei punti corrisponde ai pesi utilizzati per la lineare si adatta alla legenda mostrata a destra. Per fornire il contrasto, la soglia superiore di colormap per i pesi è stata fissata a 40. Le curve di sintonia per i due punti che si trovano significativamente al di fuori della linea di tendenza in(B) sono mostrate in Figura 4-figure supplement 1B.(C,D) Tassi di sparamento dalla Scimmia A per le prime due unità della Figura 2A. Entrambe le unità hanno una PD azimutale vicino a -135∘. Le prime tre barre mostrano i ratei di tiro nel contesto 3D per il bersaglio che giaceva a -135∘ sul xy-plane (rosa) e i due bersagli immediatamente sopra (rosa scuro), e sotto (rosa chiaro) quel bersaglio (E). La velocità di sparo nel contesto 2D al bersaglio a -135∘ è mostrata nella quarta barra (F). L’unità 1 aveva una direzione preferita sotto il piano xy(U1;Z=61, **P=0.001). L’unità 2 aveva una direzione preferita sopra il piano xy(U2;Z=154, ***P<10-3). Nonostante questa differenza, entrambe le unità hanno mostrato un aumento della velocità di fuoco verso il bersaglio planare nel contesto 2D rispetto al contesto 3D (U1;2D,3D=114, **P=0.0098, U2;2D,3D=126, *P=0.0299).(G,H) Insieme simile di velocità di tiro da Monkey C per le prime due unità della Figura 2B. I bersagli corrispondenti sono mostrati in(I e J). Entrambe le unità avevano un PD azimutale vicino a -45∘. L’unità 1 aveva una direzione preferita sotto il xy-plane U1;Z=69, ***P<10-3). L’unità 2 aveva una direzione preferenziale sopra il piano xy(U2;Z=164, **P=0.0028). Nonostante questa differenza, entrambe le unità hanno mostrato un aumento della velocità di fuoco verso il bersaglio planare nel contesto 2D rispetto al contesto 3D (U1;2D,3D=89, *P=0,0165, U2;2D,3D=95, *P=0,0374). Le velocità di sparo sono tracciate come media ± SE (U, prove U di Mann-Whitney, n2D e n3D sono le stesse della Figura 2A,B). I dati per ricreare questi diagrammi sono disponibili in Figura 4 dati fonte 1.DOI:
http://dx.doi.org/10.7554/eLife.21409.01810.7554/eLife.21409.019Cifre dati a 4 fonti 1.Variazione del campo di sintonia rispetto agli angoli di elevazione e al set di dati delle variazioni neuronali accoppiate.DOI:http://dx.doi.org/10.7554/eLife.21409.019DOI:
http://dx.doi.org/10.7554/eLife.21409.019DOI:
http://dx.doi.org/10.7554/eLife.21409.019(A) Gli effetti dose-risposta nelle modifiche di sintonia sono mostrati per Monkey A (sinistra) e Monkey C (destra). Il rapporto tra le gamme dinamiche 3D planari e 2D è tracciato contro il coseno dell’angolo di elevazione (ϕ) dei vettori PD. Gli adattamenti lineari ponderati per i punti dei dati sono mostrati in nero. Gli accoppiamenti hanno pendenze positive. bA=0,397, FA=63,6, P<10-13, nA=471, bC=0,152, FC=8,92, P=0,00299, nC=409.b, pendenza, F, F-test rispetto al modello costante, n, numero di unità analizzate. L’oscurità dei punti corrisponde ai pesi utilizzati per la lineare si adatta alla legenda mostrata a destra. Per fornire il contrasto, la soglia superiore di colormap per i pesi è stata fissata a 40.(B) Le curve di sintonia per i due punti che si trovano significativamente al di fuori della linea di tendenza per la Scimmia C. I grafici mostrano le curve di sintonia per i bersagli che giacciono sul piano xy nei contesti 2D (linea continua) e 3D (linea tratteggiata). I ratei di sparo sono indicati come media ± SE. I tassi di tiro medi minimi e massimi tra l’insieme di tutti i 26 bersagli del contesto 3D sono disegnati come linee orizzontali tratteggiate. Le curve di sintonia e le linee minime e massime sono colorate (da scuro ad arancione chiaro) secondo l’ordine di blocco dei dati (dal primo al terzo blocco). Le curve di sintonia mostrano una risposta rumorosa ai target nel piano xy con intervalli stimati ridotti nel contesto 2D. I dati per ricreare questi grafici sono disponibili nella figura 4-figure supplement 1-source data 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.02010.7554/eLife.21409.021Figure 4-figure supplement 1-source data set di dati 1.Tuning range change versus elevation angle and outlier neural tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.021DOI:
http://dx.doi.org/10.7554/eLife.21409.021DOI:
http://dx.doi.org/10.7554/eLife.21409.021

Figura 4-figure supplement 1-source data 1.Effetti di dose-risposta nelle variazioni di velocità di sparo.variazione dell’intervallo di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale anomala.variazione dell’intervallo di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale anomala.variazione dell’intervallo di sintonizzazione rispetto agli angoli di elevazione e alle curve di sintonizzazione neurale anomala.variazione dell’intervallo di sintonizzazione rispetto all’insieme di dati.(A) Gli effetti dose-risposta nei cambiamenti di sintonia sono mostrati per Monkey A (sinistra) e Monkey C (destra). Il rapporto tra le gamme dinamiche 3D planari e 2D è tracciato contro il coseno dell’angolo di elevazione (ϕ) dei vettori PD. Gli adattamenti lineari ponderati per i punti dei dati sono mostrati in nero. Gli accoppiamenti hanno pendenze positive. bA=0,397, FA=63,6, P<10-13, nA=471, bC=0,152, FC=8,92, P=0,00299, nC=409.b, pendenza, F, F-test rispetto al modello costante, n, numero di unità analizzate. L’oscurità dei punti corrisponde ai pesi utilizzati per la lineare si adatta alla legenda mostrata a destra. Per fornire il contrasto, la soglia superiore di colormap per i pesi è stata fissata a 40.(B) Le curve di sintonia per i due punti che si trovano significativamente al di fuori della linea di tendenza per la Scimmia C. I grafici mostrano le curve di sintonia per i bersagli che giacciono sul piano xy nei contesti 2D (linea continua) e 3D (linea tratteggiata). I ratei di sparo sono indicati come media ± SE. I tassi di tiro medi minimi e massimi tra l’insieme di tutti i 26 bersagli del contesto 3D sono disegnati come linee orizzontali tratteggiate. Le curve di sintonia e le linee minime e massime sono colorate (da scuro ad arancione chiaro) secondo l’ordine di blocco dei dati (dal primo al terzo blocco). Le curve di sintonia mostrano una risposta rumorosa ai target nel piano xy con intervalli stimati ridotti nel contesto 2D. I dati per ricreare questi grafici sono disponibili nella figura 4-figure supplement 1-source data 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.02010.7554/eLife.21409.021Figure 4-figure supplement 1-source data set di dati 1.Tuning range change versus elevation angle and outlier neural tuning curves dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.021DOI:
http://dx.doi.org/10.7554/eLife.21409.021DOI:
http://dx.doi.org/10.7554/eLife.21409.021
Altre proprietà di questo effetto
Il processo di adattamento sembrava avvenire rapidamente con il passaggio dal contesto 3D a quello 2D. Al fine di indagare il percorso temporale di questo processo, abbiamo ideato un metodo per stimare le variazioni del campo dinamico in base a prove di prova (vedi Materiali e metodi). In breve, abbiamo adattato i modelli di regolazione del coseno da prove in entrambi i contesti 2D e 3D. Questi modelli rappresentano una previsione della risposta della popolazione prevista per ogni contesto che può essere valutata prova per prova. Indagando l’errore di adattamento di ogni modello quando il soggetto sperimenta una transizione tra il 3D e il 2D, possiamo valutare quanto velocemente la popolazione passa dalla risposta prevista in 3D alla risposta prevista in 2D. Per mitigare il rumore, abbiamo normalizzato l’errore atteso per ogni neurone con l’errore residuo medio per i contesti 2D e 3D, e abbiamo fatto una media tra tutti i neuroni e tra le molteplici sessioni di registrazione per ogni scimmia. Si noti che tutti gli errori sono stati convalidati in modo incrociato: abbiamo inserito modelli separati per le prove pari e dispari, e li abbiamo utilizzati per prevedere i risultati rispettivamente sulle prove pari e dispari. Abbiamo stimato l’errore per le prime 120 prove nel contesto 2D e per le ultime 60 prove planari del precedente contesto 3D. Questi errori normalizzati e mediati sono mostrati nella Figura 5. Le trame mostrano uno spostamento molto rapido nella sintonizzazione della popolazione man mano che il contesto passa dal 3D al 2D. Immediatamente dopo il passaggio dal 3D al 2D (nella prova 1), l’errore del modello 3D cresce considerevolmente. Presumibilmente, la mancanza di movimento nella dimensione z indica che il soggetto cambia il contesto. L’errore del modello 2D si riduce quindi. Abbiamo adattato i modelli esponenziali alla riduzione dell’errore del modello 2D per ogni scimmia, e abbiamo trovato coefficienti di decadimento esponenziale (con limiti di confidenza del 95%) di 5,3 (3,2, 16,7) prove per le scimmie A e 4,6 (3,2, 10,5) prove per le scimmie C. Poiché ogni prova richiede circa 1 s per essere eseguita, l’effetto di riaccordatura si avvicina al completamento in pochi secondi. L’errore del modello 2D è immediatamente inferiore all’errore del modello 3D del primo trial 2D e si riduce rapidamente allo stato di base entro i primi trial.10.7554/eLife.21409.022Figure 5.Time course of adaptation.I due pannelli mostrano i corsi temporali dell’adattamento per Monkey A(A) e Monkey B(B). Gli assi ordinati nelle trame mostrano l’errore standardizzato tra i tassi di tiro nella popolazione e la risposta prevista dagli adattamenti di sintonizzazione. Ogni grafico mostra due diversi errori: l’errore basato sui modelli di sintonizzazione dal contesto 2D (blu scuro) e dal contesto 3D (rosa). Questi errori standardizzati sono mediati in più sessioni di registrazione per Monkey A (18) e Monkey C (11). Le ascisse nelle trame mostrano il numero di prova prima e dopo il passaggio dal contesto 3D al contesto 2D. I dati a destra di zero rappresentano l’errore standardizzato per le prime 120 prove nel contesto 2D. I punti di dati a sinistra di zero rappresentano le ultime 60 prove di destinazione planare del contesto 3D. La linea verticale nera tratteggiata a zero rappresenta il tempo di inattività del sistema mentre il contesto è stato commutato. Abbiamo anche tracciato gli adattamenti esponenziali (nero) all’errore del modello di sintonizzazione 2D per le prime 120 prove del contesto 2D. I dati sono stati adattati all’equazione: y=a+bexpcx. Per Monkey A, i parametri di adattamento (con limiti di confidenza del 95%) erano: a = 0,815(0,807, 0,8233); b = 0,176(0,087, 0,264); c = -0,189(-0,317, -0,060); r2 = 0,229. Per la Scimmia C, i parametri di adattamento erano: a= 0,809(0,800,0,818); b = 0,250 ( 0,150, 0,348); c = -0,202(-0,309, -0,095); r2 = 0,328. I dati per ricreare questi grafici sono disponibili nella Figura 5-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.02210.7554/eLife.21409.023Figure5-source data 1.Trial-by-trial tuning model error dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.023
Abbiamo anche valutato la completezza dell’adattamento della gamma dinamica. Per essere completa, la gamma dinamica nel contesto 2D dovrebbe eguagliare l’intera gamma dinamica nel contesto 3D, quando tutti gli obiettivi sono presi in considerazione. Abbiamo sviluppato la seguente metrica per quantificare la completezza dell’adattamento:(2)Adattamento=ρ2D-ρ3D-ρ3Dρ3Dfull-ρ3D
Qui, ρ rappresenta l’intervallo di sintonizzazione sotto un determinato contesto e un determinato set di destinazione. Il pedice indica il contesto. L’apice “completo” denota l’intero set di obiettivi per un determinato contesto, mentre la mancanza di un apice rappresenta l’insieme di obiettivi identici tra contesti. I termini usati nel calcolo di questa metrica sono descritti più dettagliatamente nella sottosezione Analisi del Tuning Range dei Metodi. Questa metrica normalizza la variazione del Tuning Range in modo tale che nessun adattamento sarebbe a zero e l’adattamento completo sarebbe a uno. Questa metrica è problematica per i neuroni in cui l’angolo di elevazione è vicino al piano xy e la differenza tra il campo di sintonizzazione completo e quello planare si avvicina a zero. Per evitare questa possibile complicazione, abbiamo limitato la nostra analisi a quei neuroni in cui sia l’angolo di elevazione è maggiore di 30∘ che il denominatore è maggiore di 2 Hz. Gli istogrammi risultanti dalle metriche per le scimmie A e C sono mostrati in Figura 6. Per entrambe le scimmie, gli istogrammi sono distribuiti significativamente lontano da zero sia con un test di segno che con un test di Wilcoxon signed-rank. Inoltre, i mezzi (±SE) della metrica sono 0,5157 (±0,1121) per la scimmia A e 0,6793 (±0,1233) per la scimmia C. Questi risultati suggeriscono che l’adattamento della gamma dinamica è più della metà completo per entrambe le scimmie. Vale la pena notare che l’adattamento del campo dinamico non è sempre completo, anche nei sistemi sensoriali. Nel sistema uditivo, Dean e colleghi hanno mostrato una gamma di capacità di rituning nei loro neuroni di esempio (cfr. Figura 1 di Dean et al. (2005)). Ohzawa ha sviluppato un indice di adattabilità per caratterizzare l’adattamento del guadagno di contrasto delle cellule nella corteccia visiva, e ha riportato valori in linea con i nostri risultati (cfr. Figura 5 di Ohzawa et al. (1985)).10.7554/eLife.21409.024Figure 6.Completezza dell’adattamento.I due pannelli mostrano istogrammi della metrica di completezza per Monkey A(A) e Monkey C(B). Per entrambi i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto zero che non rappresenta alcun adattamento della gamma dinamica. Per entrambe le scimmie, gli istogrammi sono stati distribuiti in modo significativo lontano dal punto zero (Monkey A: ***P<10-5, Wilcoxon signed-rank test, W=3580, ◊◊◊P<10-3, sign test, S=68, n=95 unità; Monkey C: ***P<10-4, W=570, ◊◊◊◊P<10-3, S=29, n=35 unità). I mezzi (± SE) della metrica sono stati 0,5157 (± 0,1121) per Monkey A e 0,6793 (± 0,1233) per Monkey C. I dati per ricreare queste trame sono disponibili nella Figura 6-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.02410.7554/eLife.21409.025Figure6-source data 1.Adaptation metric dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.025
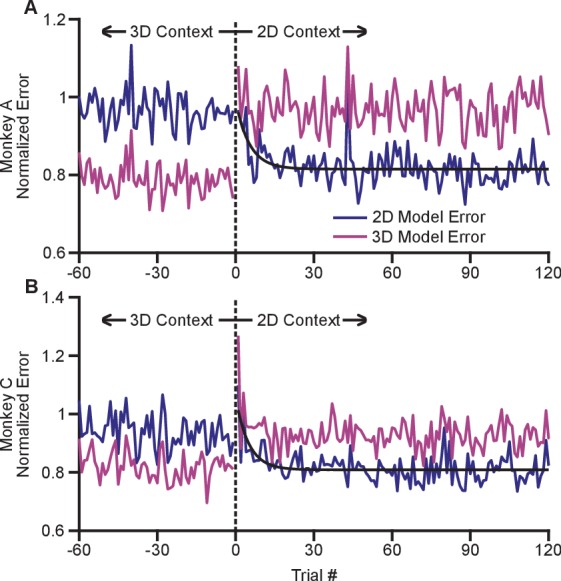
Figura 5 – Dati sorgente 1.2. Decorso temporale dell’adattamento.dataset di errore del modello di sintonia trial-by-trial.dataset di errore del modello di sintonia trial-by-trial.dataset di errore del modello di sintonia trial-by-trial.I due pannelli mostrano l’andamento temporale dell’adattamento per Monkey A(A) e Monkey B(B). Gli assi ordinati nei diagrammi mostrano l’errore standardizzato tra i tassi di tiro nella popolazione e la risposta prevista dagli adattamenti di sintonizzazione. Ogni grafico mostra due diversi errori: l’errore basato sui modelli di sintonizzazione dal contesto 2D (blu scuro) e dal contesto 3D (rosa). Questi errori standardizzati sono mediati in più sessioni di registrazione per Monkey A (18) e Monkey C (11). Le ascisse nelle trame mostrano il numero di prova prima e dopo il passaggio dal contesto 3D al contesto 2D. I dati a destra di zero rappresentano l’errore standardizzato per le prime 120 prove nel contesto 2D. I punti di dati a sinistra di zero rappresentano le ultime 60 prove di destinazione planare del contesto 3D. La linea verticale nera tratteggiata a zero rappresenta il tempo di inattività del sistema mentre il contesto è stato commutato. Abbiamo anche tracciato gli adattamenti esponenziali (nero) all’errore del modello di sintonizzazione 2D per le prime 120 prove del contesto 2D. I dati sono stati adattati all’equazione: y=a+bexpcx. Per Monkey A, i parametri di adattamento (con limiti di confidenza del 95%) erano: a = 0,815(0,807, 0,8233); b = 0,176(0,087, 0,264); c = -0,189(-0,317, -0,060); r2 = 0,229. Per la Scimmia C, i parametri di adattamento erano: a= 0,809(0,800,0,818); b = 0,250 ( 0,150, 0,348); c = -0,202(-0,309, -0,095); r2 = 0,328. I dati per ricreare queste trame sono disponibili nella Figura 5 – dati fonte 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.02210.7554/eLife.21409.023Figure 5-source data set di dati 1.Trial-by-trial tuning model error dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.023DOI:
http://dx.doi.org/10.7554/eLife.21409.023DOI:
http://dx.doi.org/10.7554/eLife.21409.023
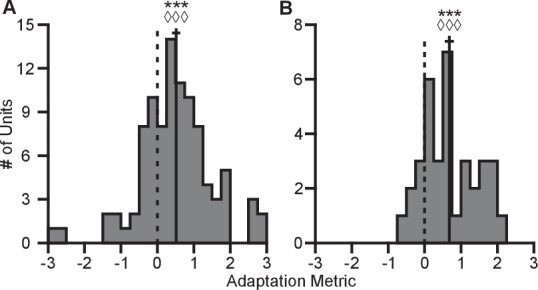
Figura 6 – Dati sorgente 1.Completezza dell’insieme di dati metrici dell’adattamento.I due pannelli mostrano gli istogrammi della completezza metrica per Monkey A(A) e Monkey C(B). Per entrambi i pannelli: linee verticali piene, mezzi di distribuzione; linee orizzontali piene, media ± SE; linee verticali tratteggiate, punto zero che non rappresenta alcun adattamento della gamma dinamica. Per entrambe le scimmie, gli istogrammi sono stati distribuiti in modo significativo lontano dal punto zero (Monkey A: ***P<10-5, Wilcoxon signed-rank test, W=3580, ◊◊◊P<10-3, sign test, S=68, n=95 unità; Monkey C: ***P<10-4, W=570, ◊◊◊◊P<10-3, S=29, n=35 unità). I mezzi (± SE) della metrica erano 0,5157 (± 0,1121) per Monkey A e 0,6793 (± 0,1233) per Monkey C. I dati per ricreare queste trame sono disponibili nella Figura 6 – dati fonte 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.02410.7554/eLife.21409.025Cifre dati a 6 fonti 1.Set di dati metrici di adattamento.DOI:http://dx.doi.org/10.7554/eLife.21409.025DOI:
http://dx.doi.org/10.7554/eLife.21409.025DOI:
http://dx.doi.org/10.7554/eLife.21409.025
Nessun adattamento con il compito di controllo manuale
BCI fornisce un potente quadro di riferimento per affrontare le questioni scientifiche di base sul controllo dei motori, compresi gli effetti di adattamento della gamma dinamica qui osservati, perché l’effetto che ogni neurone ha sul movimento del cursore è completamente specificato dallo sperimentatore, e perché possiamo ovviare a fattori complicanti come la gravità e l’inerzia(Golub et al., 2016). Tuttavia, è interessante confrontare i risultati del BCI con un compito simile eseguito in controllo manuale. Abbiamo fatto eseguire ad una terza scimmia (Monkey N) un compito di centratura con il cursore controllato dalla posizione di un marcatore di tracciamento 3D posto sulla mano della scimmia. Per i movimenti 2D, la posizione z del marcatore è stata azzerata in modo che la profondità del marcatore non avesse alcun effetto sul cursore. Abbiamo calcolato gli intervalli di sintonia per i neuroni sintonizzati direzionalmente tra l’insieme di obiettivi identici per ogni contesto (Figura 7). A differenza del compito BCI, non vediamo alcuna prova di adattamento della gamma dinamica nella versione per il controllo manuale di questo compito. Si specula sulle ragioni di ciò nella sezione Discussione.10.7554/eLife.21409.026Figure 7.Tuning range in hand-control task.Il grafico mostra l’istogramma della differenza del tuning range tra i contesti 2D e 3D per i target planari nel hand-control task. Per il grafico: linea verticale solida, media di distribuzione; linea orizzontale solida, media ± SE; linea verticale tratteggiata, punto di uguaglianza tra i due campi di sintonia. Per Monkey N, gli intervalli di sintonia non erano significativamente diversi tra il contesto 2D e 3D (n.s.P=0.6349, test Wilcoxon signed-rank, W=969, n.s.P=0.9007, S=31, n=64 unità). I dati per ricreare questi grafici sono disponibili in Figura 7-source data 1.DOI:http://dx.doi.org/10.7554/eLife.21409.02610.7554/eLife.21409.027Figure7-source data 1.Hand-control task tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.027
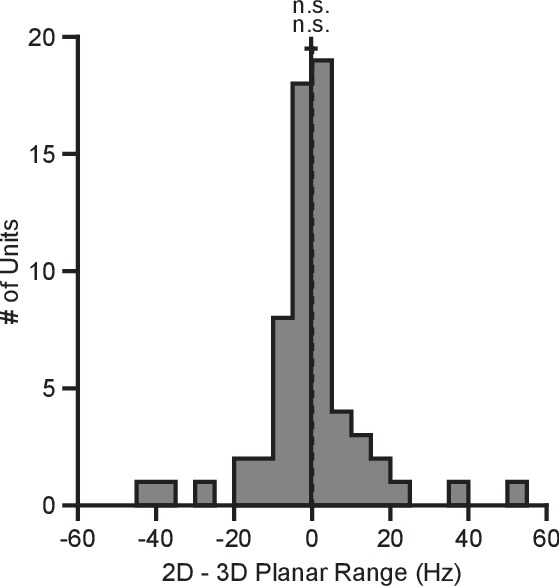
Figura 7 – Dati sorgente 1.Intervallo di sintonizzazione nel set di dati dell’intervallo di sintonizzazione del task di controllo manuale.Il grafico mostra l’istogramma della differenza del campo di sintonizzazione tra il contesto 2D e 3D per i target planari nel compito di controllo manuale. Per il grafico: linea verticale solida, media di distribuzione; linea orizzontale solida, media ± SE; linea verticale tratteggiata, punto di uguaglianza tra i due campi di sintonia. Per Monkey N, gli intervalli di sintonia non erano significativamente diversi tra il contesto 2D e 3D (n.s.P=0.6349, test Wilcoxon signed-rank, W=969, n.s.P=0.9007, S=31, n=64 unità). I dati per ricreare questi grafici sono disponibili in Figura 7 – dati sorgente 1.1. DOI:
http://dx.doi.org/10.7554/eLife.21409.02610.7554/eLife.21409.027Figure 7-source data set di dati 1.Hand-control task tuning range dataset.DOI:http://dx.doi.org/10.7554/eLife.21409.027DOI:
http://dx.doi.org/10.7554/eLife.21409.027DOI:
http://dx.doi.org/10.7554/eLife.21409.027
Discussione
I neuroni nelle regioni sensoriali codificano e trasmettono informazioni sull’ambiente esterno(Borst e Theunissen, 1999). I neuroni sensoriali subiscono anche un adattamento della gamma dinamica con cambiamenti contestuali dell’ambiente(Ohzawa et al., 1985; Dean et al., 2005). Nel nostro studio, i neuroni M1 mostrano cambiamenti significativi nella loro velocità di fuoco verso obiettivi identici, quando il contesto del compito passa dal 3D al 2D. Questi cambiamenti sono diffusi in tutta la popolazione registrata. I cambiamenti osservati non sono coerenti con una strategia di ri-orientamento durante il contesto 2D. Inoltre, i cambiamenti osservati non sono coerenti con i cambiamenti della velocità prevista tra i due contesti. Invece, i cambiamenti osservati sembrano essere coerenti con l’adattamento della gamma dinamica.
Durante il contesto 2D, la dimensione z viene aggiunta allo spazio nullo rilevante per il compito. Senza l’adattamento osservato, la porzione di campo dinamico che codifica la dimensione z durante il contesto 3D non verrebbe utilizzata durante il contesto 2D. I nostri risultati hanno mostrato che le unità cominciano ad utilizzare quella porzione del campo dinamico per codificare i target nel piano xy quando il contesto del task passa dal 3D al 2D. Questi risultati sono marcatamente simili agli adattamenti del campo dinamico che si verificano nelle regioni sensoriali. Proprio come i neuroni nella retina e nella corteccia visiva regolano la loro sintonia per codificare l’attuale gamma di intensità luminose, le unità registrate hanno regolato la loro sintonia per codificare l’attuale gamma di bersagli nel contesto dato del compito BCI.
I ricercatori hanno descritto l’adattamento della gamma dinamica nei sistemi sensoriali come funzionamento per ottimizzare il flusso di informazioni delle popolazioni neurali(Brenner et al., 2000; Fairhall et al., 2001; Wark et al., 2007). Lo stesso processo sembra funzionare in questo caso. Proprio come le pendenze delle curve di sintonia nel sistema visivo aumentano per trasmettere più informazioni su una gamma più stretta di intensità luminose, le pendenze delle curve di sintonia delle unità M1 aumentano per trasmettere più informazioni su una gamma più stretta di direzioni di destinazione.
Altri studi hanno notato cambiamenti di sintonizzazione dei singoli neuroni durante le attività di apprendimento della BCI(Jarosiewicz et al., 2008; Ganguly e Carmena, 2009; Ganguly et al., 2011; Chase et al., 2012). Tuttavia, l’adattamento della gamma dinamica che vediamo sembra essere fondamentalmente diverso dagli effetti mostrati in questi studi. In primo luogo, la scala temporale dell’adattamento della gamma dinamica è dell’ordine dei secondi(Figura 5). La scala temporale delle variazioni della sintonia neurale legate all’apprendimento di BCI è dell’ordine di decine di minuti(Jarosiewicz et al., 2008; Chase et al., 2012) fino a giorni(Ganguly e Carmena, 2009; Ganguly et al., 2011). In secondo luogo, l’adattamento della gamma dinamica è limitato ai cambiamenti di profondità della sintonia; i cambiamenti nella direzione preferita sono minimi. Negli studi di apprendimento della BCI, anche le direzioni preferite cambiano di solito. In terzo luogo, l’adattamento della gamma dinamica si verifica senza alcuna pressione di apprendimento evidente. Negli studi di apprendimento BCI, la mappatura tra l’attività neurale e i movimenti del cursore viene modificata in modo tale da compromettere le prestazioni del compito. In questo caso non è stato così: se il soggetto avesse continuato ad utilizzare le stesse velocità di scatto nei contesti 3D e 2D, le prestazioni sarebbero rimaste inalterate. Per questi motivi, ipotizziamo che l’adattamento della gamma dinamica rappresenti un ulteriore grado di flessibilità nelle risposte dei neuroni nel sistema motorio.
Mentre abbiamo osservato un adattamento coerente della gamma dinamica tra il contesto 2D e 3D nel compito BCI, non l’abbiamo osservato nella versione per il controllo manuale di questo compito. Ci sono diverse possibili ragioni per questo. Nel controllo manuale, centinaia di migliaia di neuroni contribuiscono probabilmente ai movimenti del braccio, e la variazione complessiva della gamma dinamica potrebbe essere distribuita su tutti i neuroni, rendendoli difficili da osservare. In BCI, solo i neuroni registrati contribuiscono al movimento del cursore, il che potrebbe potenzialmente rendere l’effetto più facile da vedere. Un’altra possibilità è che il numero di parametri di movimento che un singolo neurone sintonizza per il controllo manuale è abbastanza grande, e quando si passa dal 3D al 2D, la variazione percentuale del numero di parametri di controllo è piccola. In BCI, ogni neurone contribuisce solo ai movimenti 3D o 2D del cursore, il che potrebbe anche rendere l’effetto più facile da osservare. Una terza possibilità intrigante è che il controllo manuale e i movimenti BCI richiamano schemi di controllo fondamentalmente diversi. Lo studio di Hepp-Reymond ha notato un ridimensionamento della sintonizzazione quando la gamma di forze richieste in uscita è stata modificata(Hepp-Reymond et al., 1999). Tale studio è stato eseguito in condizioni isometriche, cioè i movimenti non erano fisicamente richiesti. Humphrey e colleghi hanno fatto eseguire ai soggetti movimenti di flessione/estensione del polso(Humphrey et al., 1970) in varie condizioni di carico, e hanno notato che i coefficienti di regressione per la decodifica sono stati scalati con il carico. In questo caso, abbiamo usato un compito BCI in cui i soggetti non erano fisicamente tenuti a muoversi, e i nostri soggetti tendono a mostrare pochissimo movimento fisico durante questi compiti. Al contrario, la versione a comando manuale di questo compito richiedeva movimenti fisici del braccio, ma non variazioni della forza di uscita. È possibile che l’adattamento della gamma dinamica nel sistema motore avvenga solo in condizioni di variazione della forza. Se questo è vero, ciò suggerisce che la produzione di forza isometrica è un’analogia più vicina al BCI rispetto ai movimenti palesi di raggiungimento a cui è tipicamente paragonata.
La direzione come componente importante del segnale di controllo è innegabile. Sebbene sia stato dimostrato che la sintonizzazione direzionale cambia in modo dipendente dal contesto, va sottolineato che la sintonizzazione direzionale è stabile attraverso le ripetizioni all’interno della stessa condizione. Sono stati osservati cambiamenti della funzione di sintonizzazione della direzione preferita e della profondità di modulazione tra controllo cerebrale e controllo manuale(Taylor et al., 2002; Carmena et al., 2003; Lebedev et al., 2005), tra movimenti in diversi intervalli di velocità(Moran e Schwartz, 1999; Churchland e Shenoy, 2007), e tra movimenti in diverse posture(Scott e Kalaska, 1995; Sergio e Kalaska, 2003). La sintonia può cambiare durante l’apprendimento, quando ci si adatta alle perturbazioni visuo-motorie(Wise et al., 1998; Paz et al., 2003; Mandelblat-Cerf et al., 2009), alle perturbazioni del campo di forza(Gandolfo et al., 2000; Arce et al, 2010), i cambiamenti del decodificatore BCI(Jarosiewicz et al., 2008; Ganguly e Carmena, 2009; Hwang et al., 2013), o anche l’accoppiamento coerente di spunti sensoriali con azioni premiate(Zach et al., 2008). Qui troviamo un altro esempio di cambiamento di sintonia: l’adattamento della gamma dinamica. Una caratteristica che distingue l’adattamento della gamma dinamica da questi altri tipi di cambiamenti di sintonia è che, utilizzando un principio di elaborazione delle informazioni (cioè che la gamma totale di tiro è ridimensionata secondo le statistiche di uscita), le curve di sintonia dal contesto 2D possono essere previste dal contesto 3D. Alcuni tipi di adattamento della gamma dinamica, come la normalizzazione del guadagno di contrasto nel sistema visivo, sono stati collegati ad un meccanismo di normalizzazione divisiva(Carandini et al., 1997). Definendo meglio quali aspetti del comportamento portano a cambiamenti di sintonia e da descrizioni più complete dei fattori che guidano questi cambiamenti, otterremo una comprensione più profonda delle operazioni neurali che avvengono durante il controllo del movimento.
Questi risultati supportano l’ipotesi che i neuroni in M1 servano a trasmettere in modo efficiente informazioni codificate contestualmente. L’apprendimento motorio in ambienti dinamici può essere visto come l’apprendimento di modi efficienti per codificare le informazioni. I cambiamenti nel contesto ambientale, come l’uso degli strumenti, possono portare a cambiamenti nell’associazione tra l’attività M1 e la potenza motoria(Quallo et al., 2012). Anche durante le portate tipiche in un ambiente statico, i neuroni M1 codificano in modo efficiente le informazioni relative all’attività. La funzione comune di sintonizzazione lineare(Georgopoulos et al., 1982) massimizza l’entropia di uscita per una distribuzione uniforme delle direzioni di destinazione in un ambiente 3D. Questa ‘equalizzazione dell’istogramma’ massimizza la trasmissione di informazioni nel limite di bassa rumorosità (Nadale Parga, 1994; Laughlin , 1981). Nei nostri studi, le unità in M1 hanno campi dinamici limitati con cui codificare il movimento del cursore nei diversi contesti. Invece di utilizzare un sottoinsieme delle gamme di sintonia disponibili, la popolazione visualizza in modo adattivo nuovi schemi di codifica che utilizzano pienamente le gamme delle unità che compongono la popolazione. Questo apprendimento adattivo della popolazione M1 permette di codificare in modo efficiente le informazioni rilevanti per il compito in ambienti mutevoli.
Materiali e metodi
Paradigma comportamentale e registrazione
I metodi di formazione comportamentale e di decodifica hanno seguito da vicino quelli descritti da Jarosiewicz et al. (2008). In breve, due scimmie Rhesus di sesso maschile sono state addestrate a svolgere un compito di centralità in un ambiente virtuale 3D. Le scimmie si sono sedute su una sedia da primate di fronte a uno specchio che riflette un’immagine 3D da un monitor di un computer stereoscopico. Prima dell’impianto degli elettrodi, la scimmia è stata addestrata a muovere la mano, dotata di un marcatore ottico, per spostare un cursore dal centro di un cubo immaginario a bersagli in posizione distesa in uno degli otto angoli per una ricompensa liquida(Reina et al., 2001).
Una volta che le scimmie sono diventate abili nel compito di raggiungere il centro-esterno in 3D, sono state impiantate con array di registrazione cronica. Ad entrambe le scimmie è stato impiantato un array di 96 canali (Cyberkinetics Neurotechnology Systems, Inc.). Gli impianti sono stati posizionati visivamente nell’area del braccio prossimale della corteccia motoria primaria. Le registrazioni sono state amplificate, filtrate e ordinate on-line con un sistema MAP a 96 canali Plexon MAP (Plexon Inc.). Ogni scimmia è stata addestrata ad eseguire il compito di centro-uscita con entrambi i bracci trattenuti modulando l’attività di spiking delle unità registrate per controllare la velocità del cursore. Entrambe le scimmie sono diventate abili nel compito di controllo del cervello in entrambi i contesti 2D e 3D dalle sessioni di addestramento prima di iniziare questo studio.
Ogni prova è iniziata con la scimmia che teneva il cursore all’origine dello spazio del compito per un periodo randomizzato (50-160 ms). L’obiettivo è stato presentato dopo questo periodo. L’attività richiedeva che la scimmia raggiungesse l’obiettivo entro il periodo di 2 s e che tenesse il cursore sulla posizione dell’obiettivo per un periodo randomizzato (0-100 ms). Il cursore è stato poi automaticamente riportato nella posizione di partenza per l’inizio della prova successiva. Per le prove di successo è stato consegnato un premio per l’acqua. I bersagli sono stati posizionati ad una distanza di 85 mm dal centro. Il cursore e i bersagli avevano un raggio di 8 mm ciascuno. Tutte le procedure sono state eseguite in conformità con le linee guida del Comitato istituzionale per la cura e l’uso degli animali dell’Università di Pittsburgh.
Algoritmo di decodifica
Ogni sessione di registrazione è iniziata con una sessione di controllo del cervello di calibrazione. La sessione di calibrazione ha seguito i metodi descritti da Chase et al. (2009). I parametri di decodifica sono stati inizialmente randomizzati. Sono stati poi presentati otto target del contesto 3D (quelli che giacciono agli angoli di un cubo), individualmente in ordine casuale, e sono rimasti fino alla fine del periodo di movimento. Sebbene il cursore non si sia mosso molto durante il periodo di movimento a causa dei parametri randomizzati, i tassi di cottura sono stati comunque modulati per la presentazione dei target. Una volta completato un ciclo che comprendeva una presentazione di ciascuno degli otto bersagli, i ratei di cottura sono stati regrediti usando la funzione di regressione in Matlab (Mathworks, Inc., Natick, MA) contro la direzione del bersaglio secondo il modello di sintonizzazione lineare:(3)ri=b0,i+mi𝐝⋅𝐩i
In un sottoinsieme di sessioni di registrazione, sono state effettuate sessioni di calibrazione separate per le prove 2D e 3D. Queste sessioni di calibrazione sono state condotte immediatamente prima dell’inizio del rispettivo blocco di contesto. La sessione di calibrazione per le prove 2D si differenziava dai metodi di calibrazione precedentemente descritti solo per il fatto che il set di target comprendeva 8 target equamente distanziati attorno ad un cerchio centrato nel xy-plane. Per tutte le altre sessioni di registrazione, i parametri di decodifica derivati dalla sessione di calibrazione iniziale sono stati utilizzati per l’intera sessione di registrazione.
I decodificatori lineari (PVA e OLE) sono stati utilizzati per decodificare i segnali neurali in movimento del cursore. Si è supposto che la popolazione registrata seguisse la funzione di sintonizzazione lineare descritta nell’equazione 3. Per ogni unità, i, i conteggi dei picchi sono stati misurati a 30 Hz e convertiti in velocità di scatto, ri, dividendo per l’intervallo di campionamento. I tassi sono stati mediati attraverso gli ultimi cinque contenitori di tempo e normalizzati sottraendo il tasso di cottura di base fit e dividendo per la profondità di modulazione fit: (4) ui = ri-b0,imi
I tassi normalizzati delle N unità che compongono la popolazione sono stati raggruppati nel vettore u=[u1,u2,…,uN]⊺. Analogamente, i vettori di direzione preferiti delle N unità sono stati raggruppati nella matrice P=[𝐩1,𝐩2,…,𝐩N]. Per il decoder PVA, i tassi normalizzati, 𝐮, sono stati convertiti in velocità del cursore, 𝐯, come:(5)v=ksnDNP⊺u
dove nD è il numero delle dimensioni del movimento (2 o 3) e ks è il fattore di velocità per convertire la velocità normalizzata in una velocità fisica in mm/s (i valori utilizzati nel nostro studio andavano da 65 a 120). Per i decoder OLE, le velocità normalizzate sono state convertite in velocità del cursore come:(6)v=ks(B⊺B)-1B⊺(ri-b0,i)
dove B=[m1p1,m2p2,…,mNpN]. La posizione del cursore, 𝐜, è stata aggiornata ad ogni intervallo di campionamento come:(7)𝐜(t)=𝐜(t-Δt)+Δt𝐯(t)
Per le prove nel contesto 2D, la componente z della velocità decodificata è stata impostata a zero per limitare il movimento al piano xy.
Analisi del campo di sintonia
Le analisi di questo lavoro si concentrano sui tassi di cottura delle unità registrate, ri. Questi tassi sono funzioni di molte variabili diverse: il contesto del compito (cioè il numero di dimensioni del movimento, nD), la direzione del bersaglio (𝐝), il numero di prova per il bersaglio (j) e i punti temporali all’interno della prova (t). Per una data sessione di scimmia e di registrazione, i tassi delle N unità che compongono la popolazione sono stati raggruppati nel vettore r=[r1,r2,…,rN]⊺. In questo lavoro, abbiamo analizzato il tasso medio di cottura durante la durata della prova, ⟨𝐫⟩t. Questi tassi di cottura mediati nel tempo sono stati anche mediati nel corso delle prove per un determinato contesto e un determinato obiettivo, ⟨𝐫⟩t,j. Questi tassi di tiro medi di prova e di tempo rimangono in funzione del contesto e dell’obiettivo del compito, 𝐟(nD,𝐝)=⟨𝐫⟩t,j. Abbiamo definito il target impostato, A, come target impostato nel contesto 3D, A={d:nD=3}. Questo set comprendeva 26 target, |A|=26. Abbiamo definito il target impostato, B, come target impostato nel contesto 2D, B={d:nD=2}. Questo set comprendeva 16 bersagli, |B|=16. C’erano otto obiettivi comuni ai due set, |A∩B|=8. Abbiamo definito quell’intersezione come l’insieme degli obiettivi comuni, C=A∩B. Il range planare 3D per le unità della popolazione era definito come:(8)ρ3D=max{f(nD,d):nD=3,d∈C}-min{f(nD,d):nD=3,d∈C}.
Sebbene tutti i target nel contesto 2D si trovino nel piano xy-, abbiamo calcolato l’intervallo 2D sull’insieme dei target comuni per confrontare direttamente gli intervalli:(9)ρ2D=max{f(nD,d):nD=2,d∈C}-min{f(nD,d):nD=2,d∈C}
La nostra analisi ha confrontato la differenza tra il range planare 3D (ρ3D) e il range 2D (ρ2D) per le unità che compongono la popolazione. Per il confronto degli intervalli di sintonizzazione completi, l’intervallo 2D completo è stato calcolato sull’intero set di 16 obiettivi 2D, d∈B:(10)ρ2Dfull=max{f(nD,d):nD=2,d∈B}-min{f(nD,d):nD=2,d∈B}.
Allo stesso modo, l’intera gamma 3D è stata calcolata sull’intero set di 26 obiettivi 3D, d∈(A):(11)ρ3Dfull=max{f(nD,d):nD=3,d∈A}-min{f(nD,d):nD=3,d∈A}.
Punti di ri-orientamento ottimali
Al fine di testare un’ipotesi di ri-orientamento che spieghi il cambiamento dei campi di sintonia osservati, abbiamo ideato un metodo per stimare i punti di ri-orientamento ottimali per tale ipotesi. Per ogni sessione di registrazione che utilizzava l’identico set di unità per controllare il compito BCI tra i contesti, i dati sulla frequenza di sparo del controllo cerebrale nel contesto 3D tra la presentazione del target e l’acquisizione sono stati utilizzati per adattare un modello di sintonizzazione log-lineare(Koyama et al., 2010) ad ogni unità della popolazione. Il modello di sintonizzazione log-lineare è simile al modello di sintonizzazione lineare dell’Equazione 3 con l’eccezione della relazione esponenziale nel modello log-lineare:(12)rll,i(𝐝)=exp(bll,0,i+mll,i𝐝⋅𝐩ll,i)
I pedici, ll, sono usati per distinguere l’equazione e i suoi parametri di sintonia da quelli usati nel modello di sintonia lineare. I parametri di sintonizzazione sono stati adattati per ogni neurone utilizzando la funzione glmfit in Matlab con i parametri di distribuzione e di collegamento impostati rispettivamente come Poisson e log. Per ognuno degli otto obiettivi condivisi, è stato stimato un punto di ri-orientamento ottimale per il contesto 2D utilizzando i modelli di tuning lineare log e i decodificatori di ogni sessione di registrazione. L’ottimizzazione è stata eseguita in Matlab come minimizzazione vincolata per spostare il cursore più vicino al bersaglio dopo una fase di tempo. L’ottimizzazione è stata vincolata per garantire che il singolo punto di ri-orientamento per ogni target e sessione di registrazione si trovi in S2, lo spazio dei vettori unitari in R3. La minimizzazione vincolata poteva essere scritta come:(13)min{‖85d-ΔtksnDN∑i=1Npirll,i(d∗)-b0,imi‖:d∗∈S2}.
Lo scalare, 85, viene utilizzato per scalare la direzione del target alla distanza target di 85 mm utilizzata negli studi. Inoltre, si noti che le velocità di sparo previste, rll,i, sono derivate dal modello di sintonizzazione log-lineare dell’equazione 12 e decodificate utilizzando i parametri di sintonizzazione utilizzati nel decodificatore originale. Così, per tutte le direzioni del bersaglio, 𝐝, nell’insieme dei bersagli comuni, C, abbiamo ricavato i punti di mira ottimali, 𝐝*, che abbiamo raggruppato nell’insieme, D. I campi di mira ottimali sono stati calcolati come:(14)ρre-aim=max{rll(d∗):d∗∈D}-min{rll(d∗):d∗∈D}.
Allo stesso modo, l’intervallo di sintonia previsto dal modello log-lineare è stato calcolato come:(15)ρll=max{rll(d):d∈C}-min{rll(d):d∈C}.
Per ogni unità e sessione di registrazione, abbiamo calcolato il segno della differenza negli intervalli di sintonizzazione previsti dalla ri-aiming, sgn(ρre-aim,i-ρll,i), e il segno della differenza osservata negli intervalli di sintonizzazione, sgn(ρ2D,i-ρ3D,i), sommando i risultati in una tabella di contingenza.
Il corso temporale dell’adattamento
Per valutare la velocità con cui la popolazione neurale si è adattata ai cambiamenti di contesto, abbiamo creato una metrica di errore normalizzata basata su modelli di sintonizzazione di ogni contesto. Nella costruzione dei modelli di sintonizzazione, abbiamo considerato solo i tassi di sparamento per le prove in cui l’obiettivo era nell’insieme degli obiettivi comuni. Per ogni sessione e contesto, le prove sono state suddivise in due gruppi separati: prove pari e prove dispari. Abbiamo inserito modelli di sintonizzazione lineare separati per ogni gruppo. L’errore per ogni prova è stato calcolato come differenza tra la risposta della popolazione per quella prova e la risposta attesa in base al modello di sintonizzazione che si adatta al gruppo opposto come quella prova. Gli errori sono stati calcolati utilizzando sia i modelli di tuning creati dal contesto 2D sia quelli creati dal contesto 3D. Questi errori sono stati normalizzati dividendo per il rumore standardizzato dei neuroni dal tuning fit. I rumori sono stati stimati come parametro di dispersione dalla funzione Matlab glmfit utilizzata per adattare i modelli di tuning. Per standardizzare la normalizzazione tra il contesto 2D e 3D, abbiamo usato la radice quadrata del prodotto dei parametri di dispersione stimati da ogni contesto. Il valore assoluto degli errori normalizzati è stato mediato sui neuroni della popolazione. Per ogni scimmia, gli errori di prova sono stati mediati su più sessioni di registrazione per creare le metriche di errore normalizzate finali visualizzate nella Figura 5. Per il contesto 3D, gli errori potevano essere stimati solo per gli obiettivi planari. Successivamente, tutte le prove per i target non planari sono state rimosse dall’analisi. Le rimanenti prove di target planari sono state ordinate come ultima prova di target planari, dalla penultima all’ultima, e così via al fine di calcolare la media delle sessioni di registrazione.
Durante la tracciatura di questi errori normalizzati, abbiamo notato una tendenza ad una rapida diminuzione dell’errore del modello di sintonia 2D nelle prime prove del contesto 2D. Al fine di modellare tale calo dell’errore, abbiamo inserito una funzione esponenziale nei dati della media delle sessioni. La funzione esponenziale ha seguito l’equazione: y=a+bexp(cx), dove y era la metrica dell’errore e x era il numero di prova. Nel nostro lavoro, utilizziamo il parametro fit c per descrivere la rapida diminuzione della metrica dell’errore. Questi accoppiamenti sono mostrati nella Figura 5.
Attività di controllo manuale
Al fine di studiare se l’adattamento della gamma dinamica si verifica sotto un paradigma di controllo manuale, abbiamo condotto un esperimento simile in cui il movimento del cursore è stato controllato direttamente attraverso la mano di una scimmia. Una terza scimmia (Monkey N) è stata addestrata ad usare la sua mano per controllare il movimento del cursore di un computer in un compito che raggiunge il centro fuori(Velliste et al., 2014). Un marcatore a infrarossi è stato posizionato sul dorso della mano della scimmia e tracciato utilizzando un sistema di tracciamento ottico Optotrak 3020 (Northern Digital, Waterloo, Canada). La posizione del marcatore è stata utilizzata in tempo reale per aggiornare la posizione del cursore sul monitor del computer stereoscopico. Il cursore e i target nel paradigma del controllo manuale erano identici a quelli utilizzati nello studio sul controllo del cervello. Abbiamo studiato la risposta neurale per gli studi sia in 3D che in 2D, dove il contesto 3D precede il contesto 2D. Durante gli esperimenti nel contesto 2D, la posizione del cursore è stata fissata nel piano xy. In altre parole, il cursore sarebbe rimasto fermo se la scimmia avesse spostato la mano più vicina o più lontana dal corpo mantenendo la stessa posizione laterale e verticale.
I tassi di sparo neurale erano calcolati nelle finestre temporali tra la presentazione del bersaglio e l’acquisizione. Questi tassi sono stati calcolati in media tra le prove dello stesso bersaglio e utilizzati per stimare gli intervalli di sintonizzazione in ogni contesto. Questa analisi è stata limitata ai neuroni che erano sintonizzati direzionalmente. Per ogni contesto, abbiamo adattato un modello di sintonizzazione del coseno alle risposte del tasso di sparo all’insieme di tutti i target. I neuroni che avevano una profondità di modulazione di adattamento inferiore a 4 Hz in entrambi i contesti 2D e 3D sono stati esclusi dall’analisi. Nella Figura 7, confrontiamo la differenza negli intervalli di sintonizzazione per l’insieme dei bersagli comuni tra il contesto 2D e 3D in modo simile alla Figura 2D. Questo studio aggiuntivo e tutte le procedure associate sono state eseguite in conformità con le linee guida del Comitato istituzionale per la cura e l’utilizzo degli animali dell’Università di Pittsburgh.
References
- Arce F, Novick I, Mandelblat-Cerf Y, Vaadia E. Neuronal correlates of memory formation in motor cortex after adaptation to force field. Journal of Neuroscience. 2010; 30:9189-9198. DOI | PubMed
- Atick JJ. Could information theory provide an ecological theory of sensory processing?. Network. 2011; 22:4-44. DOI | PubMed
- Borst A, Theunissen FE. Information theory and neural coding. Nature Neuroscience. 1999; 2:947-957. DOI | PubMed
- Brenner N, Bialek W, de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron. 2000; 26:695-702. DOI | PubMed
- Carandini M, Heeger DJ, Movshon JA. Linearity and normalization in simple cells of the macaque primary visual cortex. Journal of Neuroscience. 1997; 17:8621-8644. PubMed
- Carmena JM, Lebedev MA, Crist RE, O’Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biology. 2003; 1DOI | PubMed
- Chase SM, Schwartz AB, Kass RE. Bias, optimal linear estimation, and the differences between open-loop simulation and closed-loop performance of spiking-based brain-computer interface algorithms. Neural Networks. 2009; 22:1203-1213. DOI | PubMed
- Chase SM, Schwartz AB, Kass RE. Latent inputs improve estimates of neural encoding in motor cortex. Journal of Neuroscience. 2010; 30:13873-13882. DOI | PubMed
- Chase SM, Kass RE, Schwartz AB. Behavioral and neural correlates of visuomotor adaptation observed through a brain-computer interface in primary motor cortex. Journal of Neurophysiology. 2012; 108:624-644. DOI | PubMed
- Churchland MM, Shenoy KV. Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. Journal of Neurophysiology. 2007; 97:4235-4257. DOI | PubMed
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nature Neuroscience. 2005; 8:1684-1689. DOI | PubMed
- Evarts EV. Pyramidal tract activity associated with a conditioned hand movement in the monkey. Journal of Neurophysiology. 1966; 29:1011-1027. PubMed
- Evarts EV. Relation of pyramidal tract activity to force exerted during voluntary movement. Journal of Neurophysiology. 1968; 31:14-27. PubMed
- Fairhall AL, Lewen GD, Bialek W, de Ruyter Van Steveninck RR. Efficiency and ambiguity in an adaptive neural code. Nature. 2001; 412:787-792. DOI | PubMed
- Gandolfo F, Li C, Benda BJ, Schioppa CP, Bizzi E. Cortical correlates of learning in monkeys adapting to a new dynamical environment. PNAS. 2000; 97:2259-2263. DOI | PubMed
- Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biology. 2009; 7DOI | PubMed
- Ganguly K, Dimitrov DF, Wallis JD, Carmena JM. Reversible large-scale modification of cortical networks during neuroprosthetic control. Nature Neuroscience. 2011; 14:662-667. DOI | PubMed
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. Journal of Neuroscience. 1982; 2:1527-1537. PubMed
- Georgopoulos AP, Kettner RE, Schwartz AB. Primate motor cortex and free arm movements to visual targets in three-dimensional space. II. coding of the direction of movement by a neuronal population. Journal of Neuroscience. 1988; 8:2928-2937. PubMed
- Georgopoulos AP, Ashe J, Smyrnis N, Taira M. The motor cortex and the coding of force. Science. 1992; 256:1692-1695. DOI | PubMed
- Golub MD, Chase SM, Batista AP, Yu BM. Brain-computer interfaces for dissecting cognitive processes underlying sensorimotor control. Current Opinion in Neurobiology. 2016; 37:53-58. DOI | PubMed
- Harris RA, O’Carroll DC, Laughlin SB. Contrast gain reduction in fly motion adaptation. Neuron. 2000; 28:595-606. DOI | PubMed
- Hepp-Reymond MC, Wyss UR, Anner R. Neuronal coding of static force in the primate motor cortex. Journal De Physiologie. 1978; 74PubMed
- Hepp-Reymond M, Kirkpatrick-Tanner M, Gabernet L, Qi HX, Weber B. Context-dependent force coding in motor and premotor cortical areas. Experimental Brain Research. 1999; 128:123-133. DOI | PubMed
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. The Journal of Physiology. 1962; 160:106-154. DOI | PubMed
- Humphrey DR, Schmidt EM, Thompson WD. Predicting measures of motor performance from multiple cortical spike trains. Science. 1970; 170:758-762. DOI | PubMed
- Hwang EJ, Bailey PM, Andersen RA. Volitional control of neural activity relies on the natural motor repertoire. Current Biology. 2013; 23:353-361. DOI | PubMed
- Jarosiewicz B, Chase SM, Fraser GW, Velliste M, Kass RE, Schwartz AB. Functional network reorganization during learning in a brain-computer interface paradigm. PNAS. 2008; 105:19486-19491. DOI | PubMed
- Katz Y, Heiss JE, Lampl I. Cross-whisker adaptation of neurons in the rat barrel cortex. Journal of Neuroscience. 2006; 26:13363-13372. DOI | PubMed
- Koyama S, Chase SM, Whitford AS, Velliste M, Schwartz AB, Kass RE. Comparison of brain-computer interface decoding algorithms in open-loop and closed-loop control. Journal of Computational Neuroscience. 2010; 29:73-87. DOI | PubMed
- Kuffler SW. Discharge patterns and functional organization of mammalian retina. Journal of Neurophysiology. 1953; 16:37-68. PubMed
- Kvale MN, Schreiner CE. Short-term adaptation of auditory receptive fields to dynamic stimuli. Journal of Neurophysiology. 2004; 91:604-612. DOI | PubMed
- Laughlin S. A simple coding procedure enhances a neuron’s information capacity. Zeitschrift Fur Naturforschung. Section C, Biosciences. 1981; 36:910-912. DOI | PubMed
- Lebedev MA, Carmena JM, O’Doherty JE, Zacksenhouse M, Henriquez CS, Principe JC, Nicolelis MA. Cortical ensemble adaptation to represent velocity of an artificial actuator controlled by a brain-machine interface. Journal of Neuroscience. 2005; 25:4681-4693. DOI | PubMed
- Mandelblat-Cerf Y, Paz R, Vaadia E. Trial-to-trial variability of single cells in motor cortices is dynamically modified during visuomotor adaptation. Journal of Neuroscience. 2009; 29:15053-15062. DOI | PubMed
- Maravall M, Petersen RS, Fairhall AL, Arabzadeh E, Diamond ME. Shifts in coding properties and maintenance of information transmission during adaptation in barrel cortex. PLoS Biology. 2007; 5DOI | PubMed
- Moore BR. A modification of the Rayleigh test for vector data. Biometrika. 1980; 67:175-180. DOI
- Moran DW, Schwartz AB. Motor cortical representation of speed and direction during reaching. Journal of Neurophysiology. 1999; 82:2676-2692. PubMed
- Nadal J-P, Parga N. Nonlinear neurons in the low-noise limit: a factorial code maximizes information transfer. Network: Computation in Neural Systems. 1994; 5:565-581. DOI
- Nagel KI, Doupe AJ. Temporal processing and adaptation in the songbird auditory forebrain. Neuron. 2006; 51:845-859. DOI | PubMed
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat visual cortex. Nature. 1982; 298:266-268. DOI | PubMed
- Ohzawa I, Sclar G, Freeman RD. Contrast gain control in the cat’s visual system. Journal of Neurophysiology. 1985; 54:651-667. PubMed
- Paz R, Boraud T, Natan C, Bergman H, Vaadia E. Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nature Neuroscience. 2003; 6:882-890. DOI | PubMed
- Quallo MM, Kraskov A, Lemon RN. The activity of primary motor cortex corticospinal neurons during tool use by macaque monkeys. Journal of Neuroscience. 2012; 32:17351-17364. DOI | PubMed
- Rabinowitz NC, Willmore BD, Schnupp JW, King AJ. Contrast gain control in auditory cortex. Neuron. 2011; 70:1178-1191. DOI | PubMed
- Reina GA, Moran DW, Schwartz AB. On the relationship between joint angular velocity and motor cortical discharge during reaching. Journal of Neurophysiology. 2001; 85:2576-2589. PubMed
- Schwartz AB, Kettner RE, Georgopoulos AP. Primate motor cortex and free arm movements to visual targets in three-dimensional space. I. relations between single cell discharge and direction of movement. Journal of Neuroscience. 1988; 8:2913-2927. PubMed
- Scott SH, Kalaska JF. Changes in motor cortex activity during reaching movements with similar hand paths but different arm postures. Journal of Neurophysiology. 1995; 73:2563-2567. PubMed
- Sergio LE, Kalaska JF. Systematic changes in motor cortex cell activity with arm posture during directional isometric force generation. Journal of Neurophysiology. 2003; 89:212-228. DOI | PubMed
- Shapley R, Enroth-Cugell C. Chapter 9 visual adaptation and retinal gain controls. Progress in Retinal Research. 1984; 3:263-346. DOI
- Smirnakis SM, Berry MJ, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997; 386:69-73. DOI | PubMed
- Taylor DM, Tillery SI, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002; 296:1829-1832. DOI | PubMed
- Ulanovsky N, Las L, Farkas D, Nelken I. Multiple time scales of adaptation in auditory cortex neurons. Journal of Neuroscience. 2004; 24:10440-10453. DOI | PubMed
- Velliste M, Kennedy SD, Schwartz AB, Whitford AS, Sohn JW, McMorland AJ. Motor cortical correlates of arm resting in the context of a reaching task and implications for prosthetic control. Journal of Neuroscience. 2014; 34:6011-6022. DOI | PubMed
- Wark B, Lundstrom BN, Fairhall A. Sensory adaptation. Current Opinion in Neurobiology. 2007; 17:423-429. DOI | PubMed
- Wise SP, Moody SL, Blomstrom KJ, Mitz AR. Changes in motor cortical activity during visuomotor adaptation. Experimental Brain Research. 1998; 121:285-299. DOI | PubMed
- Zach N, Inbar D, Grinvald Y, Bergman H, Vaadia E. Emergence of novel representations in primary motor cortex and premotor neurons during associative learning. Journal of Neuroscience. 2008; 28:9545-9556. DOI | PubMed
- Zar JH. Biostatistical Analysis. Prentice-Hall/Pearson: Upper Saddle River; 2010.
Fonte
Rasmussen RG, Schwartz A, Chase SM, Vaadia E () Dynamic range adaptation in primary motor cortical populations. eLife 6e21409. https://doi.org/10.7554/eLife.21409





