Abstract
Introduzione
Gli approcci empirici alla caratterizzazione dei meccanismi che governano le dinamiche cerebrali si basano spesso sull’uso simultaneo di diverse modalità di acquisizione. Questi dati possono essere fusi utilizzando modelli statistici, ma le inferenze sono vincolate dalle informazioni contenute nei diversi segnali, rendendo elusiva una comprensione meccanicistica dei processi neurofisiologici. La simulazione cerebrale è una tecnica complementare che permette l’inferenza su parametri del modello che riflettono meccanismi che sono alla base del comportamento emergente, ma che sono nascosti all’osservazione diretta(Breakspear, 2017).
I modelli di rete cerebrale sono sistemi dinamici di modelli di massa neurale accoppiati per simulare l’attività cerebrale su larga scala; l’accoppiamento è spesso mediato da stime dei punti di forza delle connessioni anatomiche basate su dati di risonanza magnetica ponderati per diffusione (la cosiddetta connettività strutturale o ‘connettomi’). Qui, sviluppiamo un nuovo tipo di modello di rete cerebrale, chiamato ‘modello ibrido’, in cui i dati EEG di ogni soggetto viene utilizzato per guidare la dinamica della massa neurale (Figura 1). In breve, siamo stati in grado di utilizzare i modelli ibridi risultanti per riprodurre le serie temporali fMRI in corso su un periodo di 20 minuti e una varietà di altri fenomeni empirici(Figura 2). A differenza dei precedenti modelli di rete cerebrale che utilizzavano il rumore come input, i modelli ibridi sono guidati dall’attività della sorgente EEG (cioè l’attività del sensore EEG mappata sulle posizioni corticali) e quindi incorporano simultaneamente le informazioni strutturali e funzionali dei singoli soggetti(Figura 1). L’attività della sorgente EEG iniettata serve come approssimazione delle correnti di ingresso sinaptiche eccitatorie (EPSCs), che aiuta ad aumentare la plausibilità biologica dell’attività del modello generato(Buzsáki et al., 2012; Haider et al., 2016; Isaacson e Scanziani, 2011; Nunez e Srinivasan, 2006). I modelli ibridi individualizzati forniscono previsioni di serie temporali di fMRI a stato di riposo specifico del soggetto in corso(Figura 3). Inoltre, diversi fenomeni empirici di diverse modalità e scale temporali sono riprodotti: topologie spaziali delle reti di connettività funzionale fMRI(Figura 4), l’inibizione dell’eccitazione (E / I) equilibrio delle correnti di ingresso sinaptiche, la relazione inversa tra α-ritmo fase e spike-firing su scale temporali a breve termine (Figura 5), e la relazione inversa tra oscillazioni di potenza in banda α e spike-firing, rispettivamente oscillazioni fMRI, su scale temporali a lungo termine (Figura 6),e la scala di potenza fMRI legge di potenza (Figura 7). Ancora più importante, la nostra successiva analisi dell’attività intrinseca del modello rivela processi neurofisiologici che potrebbero spiegare come le reti cerebrali producono i suddetti modelli di segnale(Figure 5-7). Cioè, i risultati della simulazione non solo predicono le serie temporali fMRI a riposo in corso e diversi fenomeni empirici osservati con metodi di elettrofisiologia invasiva, ma, cosa più importante, mostrano anche come l’interazione delle reti di popolazioni neurali porta all’emergere di questi fenomeni e come essi sono collegati attraverso più scale temporali in una gerarchia di scala temporale.
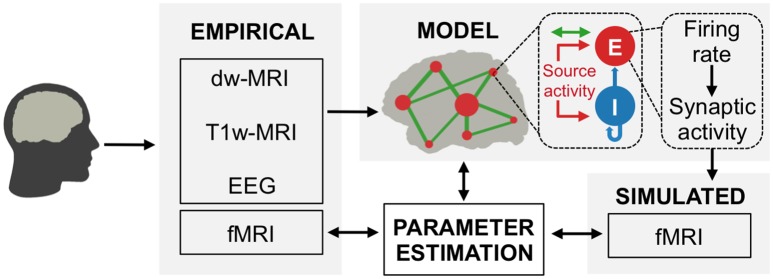
Figura 1.Struttura di modellazione ibrida.I modelli di reti cerebrali ibride sono costruiti a partire da tractografia a risonanza magnetica ponderata per diffusione e da parcelle regionali ottenute da risonanza magnetica anatomica. I nodi dei modelli ibridi sono iniettati con serie temporali di attività della sorgente EEG specifica del soggetto invece che con il rumore. Le serie temporali fMRI previste sono adatte alle serie temporali empiriche fMRI di ciascun soggetto, che sono state acquisite simultaneamente con l’EEG. Ad ogni nodo (piccoli cerchi rossi) della rete a lungo raggio (linee verdi) sono reti locali di modelli di popolazione neurali eccitatori (E) e inibitori(I) che sono guidati dall’attività della sorgente EEG (frecce rosse). I nodi sono globalmente accoppiati da connettimi strutturali (frecce verdi) che rappresentano l’eterogenea forza di accoppiamento della materia bianca tra le diverse aree cerebrali. Correnti sinaptiche di ingresso(equazioni 1 e 2), velocità di scatto(equazioni 3 e 4 ) e attività sinaptica (equazioni5 e 6) alla base delle previsioni fMRI sono analizzati per identificare come l’attività della popolazione neurale e le interazioni di rete si riferiscono a segnali di neuroimaging osservabili. Vedi anche Video 1 per una visualizzazione della costruzione del modello di rete cerebrale e dei risultati esemplari di simulazioni di modelli ibridi.
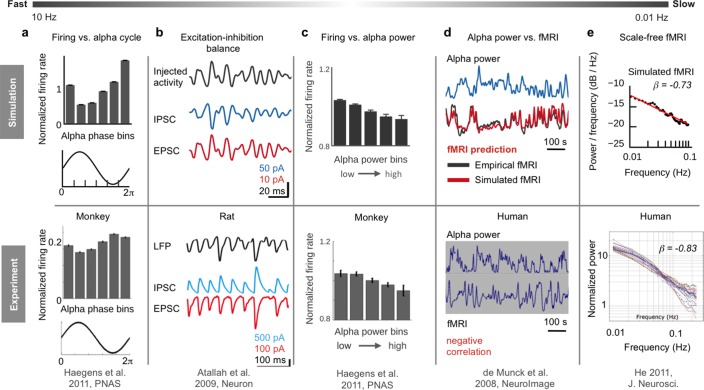
Figura 2.Figura 2. Panoramica di sei fenomeni empirici su diverse scale temporali riprodotti dal modello ibrido.(a) Il fuoco dei neuroni è inversamente correlato alla fase delle onde α: durante i picchi delle onde α, i neuroni sparano il minimo, mentre sparano il massimo durante i trogoli (adattato da Haegens et al., 2011).(b) Le nostre simulazioni indicano che la relazione inversa tra lo sparo e la fase α è legata al continuo bilanciamento dell’eccitazione e dell’inibizione neurale (adattato da Atallah e Scanziani, 2009). Ristampato con il permesso di Elsevier).(c) Su una scala temporale più lunga (<0,25 Hz), le oscillazioni delle velocità di sparo sono inversamente correlate alle fluttuazioni di potenza in banda α (adattato da Haegens et al., 2011).(d) Le simulazioni del modello suggeriscono un meccanismo che trasforma le oscillazioni di potenza in banda α in oscillazioni fMRI, prevedendo serie temporali fMRI a riposo specifiche del soggetto, modelli di rete spaziale corrispondenti e la correlazione inversa tra α-potenza e fMRI (adattato da de Munck et al., 2008. Ristampato con il permesso di Elsevier.).e) L’emergere di spettri di potenza fMRI senza scala (adattato da He, 2011) è il risultato di un input di rete a lungo raggio.(f) Sono state previste matrici di connettività funzionali individuali su finestre di tempo lunghe e brevi (adattato da Allen et al., 2014).
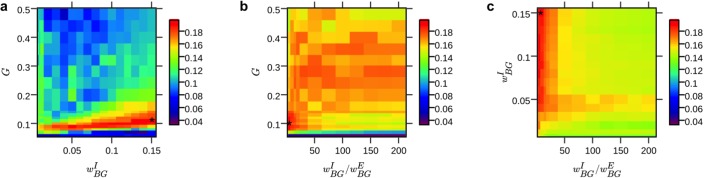
Figura 3-figure supplement 1.Figura 3—supplemento alla figura 1. Predizione delle serie temporali fMRI specifiche per la persona.a) Serie temporali esemplificative del modello ibrido e dei tre scenari di controllo di un soggetto.(b) Box plot di coefficienti di correlazione medi tra tutte le serie temporali simulate e le regioni empiriche (20,7 min) per ogni soggetto (n = 15; i valori di α-regressor sono stati invertiti a scopo illustrativo).c) Diagramma di dispersione della deviazione standard del corso del tempo RSN (s.d.) rispetto alla qualità della previsione. I punti rappresentano i dati dei nove corsi di tempo RSN per ogni soggetto.d) Confronto della qualità di previsione durante il quartile superiore e inferiore del corso temporale dell’RSN epocale s.d.s. Riga superiore: modelli di attivazione spaziale di nove RSN. Fila centrale: coefficienti di correlazione tra i modi temporali di RSN e i risultati della simulazione del modello ibrido e i tre scenari di controllo. Fila inferiore: finestra scorrevole (lunghezza: 100 scansioni fMRI = 194 s; larghezza del passo: una scansione fMRI) correlazioni per le correlazioni dei quartili superiori (primo e terzo boxplot per pannello) e inferiori (secondo e quarto boxplot per pannello) della modalità temporale RSN a finestra per il modello ibrido e il regressore α. Gli asterischi indicano un significativo aumento della qualità di previsione del modello ibrido rispetto agli scenari di controllo nel test di somma del rango Wilcoxon a una coda (*p<0,05, **p<0,01). Inoltre, tutte le correlazioni del modello ibrido in(b) e(d) sono state testate per l’ipotesi nulla che provengano da una distribuzione la cui mediana è pari a zero al livello di significatività del 5%. Tutti i test hanno respinto l’ipotesi nulla delle mediane zero, ad eccezione delle correlazioni RSN su 20 minuti per il controllo esecutivo e le reti frontoparietali (riga centrale).(a-c) 2d parametro mappe di calore spaziale parametro2d mostrano la correlazione media delle serie temporali ottenuti dal modello ibrido per diverse combinazioni dei tre parametri G, ω BGE, ω BGI (quest’ultimoraffigurato come rapporto ω BGI / ω BGE),i risultati sono stati mediati su tutti i soggetti e le regioni cerebrali. I valori dei parametri che hanno prodotto la più alta correlazione media sono stati utilizzati per le simulazioni con l’ingresso artificiale α (contrassegnato con un asterisco). Abbiamo confermato l’identificabilità del modello mostrando che la ricerca dello spazio dei parametri converge verso un’unica soluzione ottimale che fornisce le migliori previsioni.

Figura 4.Previsione funzionale della connettività.(a, b) I diagrammi di box mostrano i coefficienti di correlazione ottenuti dalla correlazione di tutte le voci sottodiagonali delle matrici FC empiriche e simulate. FC è stato calcolato per le epoche lunghe (FC statico; calcolato su 20,7 min) e per le epoche brevi (FC dinamico; correlazione finestra scorrevole media; 100 scansioni fMRI lunghezza finestra; una scansione fMRI larghezza passo passo). I risultati sono stati confrontati per(a) il set di parametri che ha generato la migliore previsione delle serie temporali fMRI e(b) il set di parametri che ha prodotto le migliori previsioni FC per ogni soggetto.c) I diagrammi di dispersione confrontano la media FC empirica e quella simulata per le simulazioni di modelli ibridi e il regressore α. I punti rappresentano tutte le correlazioni delle serie temporali delle regioni a coppie in media su tutti i soggetti. Gli asterischi in(a) e(b) indicano una qualità di previsione significativamente aumentata del modello ibrido rispetto alle condizioni di controllo nel test di somma del rango Wilcoxon a una coda (*p<0.05, **p<0.01).
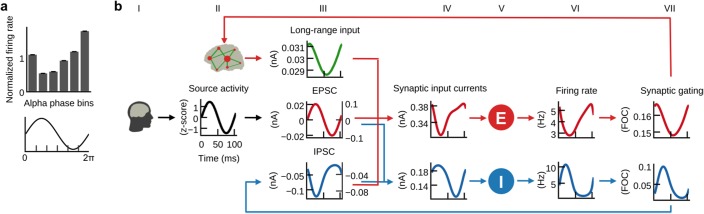
Figura 5.L’equilibrio E/I genera la relazione inversa tra la fase α e la cottura.a) Istogramma dei tassi di cottura della popolazione diviso in sei contenitori secondo i segmenti del ciclo α e normalizzato rispetto al tasso medio di cottura di ogni ciclo. I tassi di cottura della popolazione erano più alti durante la depressione e più bassi durante il picco di α-cicli.b) Grande media delle forme d’onda delle entrate e delle uscite della popolazione bloccata al tempo di α-cicli di attività della sorgente EEG iniettata (nero, colonna II). Gli assi destro e sinistro indicano rispettivamente le correnti in ingresso alle popolazioni eccitatorie e inibitorie. Si prega di fare riferimento al testo principale per una descrizione del meccanismo che spiega la relazione inversa tra α-cicli e velocità di accensione.
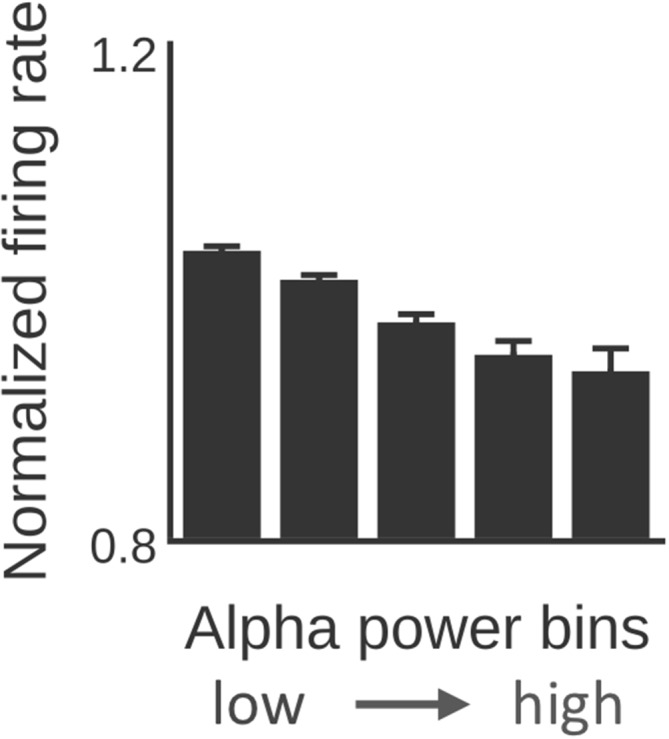
Figura 6-figure supplemento 1.α-potenza fluttuazioni generano oscillazioni fMRI.α-potenza prevede il tasso di cottura.Grande media delle forme d’onda degli ingressi e delle uscite della popolazione su scale temporali più lunghe.(a) I modelli ibridi sono stati iniettati con α-attività artificiale che consiste di oscillazioni sinusoidali a 10 Hz che contengono un singolo breve scoppio ad alta potenza (nero, colonna I; arancione: inviluppo del segnale). Mentre le deflessioni positive dell’onda α generavano deflessioni positive dei tassi di cottura della popolazione inibitoria, grandi deflessioni negative erano delimitate dal vincolo fisiologico di 0 Hz (blu, quinta colonna; nero: media mobile).b) I modelli ibridi sono stati iniettati modelli con onde sinusoidali a 10 Hz dove la potenza in corso è stata modulata in modo simile a α-ritmi empirici (0,01-0,03 Hz). Analogamente a(a), ma per un periodo di tempo più lungo, popolazioni inibitorie rettificato deflessioni negative, che ha introdotto l’α-potenza modulazione come una nuova componente di frequenza come una nuova componente di frequenza in tassi di cottura e serie temporali fMRI.Analogamente ai risultati elettrofisiologici mostrati in Haegens et al. (2011), tutte le serie temporali per ogni soggetto e regione cerebrale sono state divise in cinque contenitori di uguali dimensioni sulla base del livello di potenza α e del tasso di cottura medio (normalizzato con il tasso di cottura medio per regione cerebrale) è stato calcolato per contenitore. Il tasso di cottura è diminuito con l’aumento di α-potenza (Kruskal-Wallis/Tukey post-hoc confronto multiplo; p<0,001).
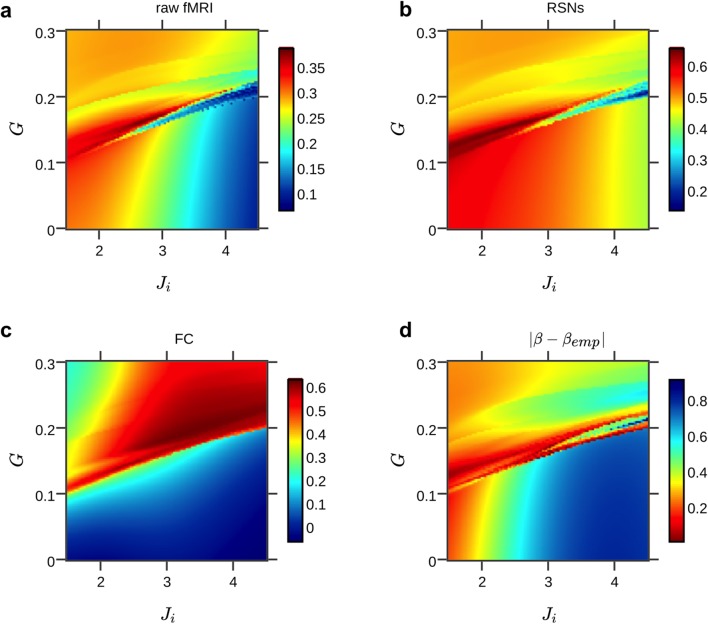
Figura 7-figure supplemento 2.Come nella Figura 7a, ma le simulazioni sono state eseguite con il modello ibrido semplificato, cioè i modelli non hanno utilizzato alcun controllo di inibizione di feedback (FIC) e un unico valore per tutte le connessioni locali inibitorie Ji è stato utilizzato.(a) Densità spettrali di potenza di fMRI simulata ed empirica e attività empirica in banda α (gli adattamenti in linea retta degli spettri di potenza sono solo a scopo illustrativo; l’invarianza di scala è stata determinata nel dominio del tempo utilizzando rigorosi criteri di selezione del modello, vedi Materiali e metodi).b) Come nella Figura 6b, ma con accoppiamento a lungo raggio disabilitato. In contrasto con la Figura 6b, le ampiezze dei tassi di cottura, gating sinaptico e fMRI sono ugualmente grandi, mentre nella Figura 6b le ampiezze erano più grandi durante le modulazioni di potenza in banda α più lente.Gli spettri fMRI empirici e simulati hanno un grande esponente della legge di potenza, cioè una pendenza più ripida, rispetto alla potenza α-potenza in corso o alla potenza a banda larga (β α-banda = -0,53, β banda larga = -0,47). Per analizzare l’effetto dell’interazione di rete a lungo raggio, la fMRI simulata è stata calcolata con e senza accoppiamento a lungo raggio. Per escludere che gli spettri di potenza emergano nonostante l’assenza dell’accoppiamento a lungo raggio, l’inibizione locale è stata regolata in modo tale che il modello producesse le più alte previsioni delle serie temporali fMRI. Senza l’accoppiamento a lungo raggio, la fMRI simulata ha mostrato un esponente simile all’attività della sorgente EEG iniettata. Quando l’accoppiamento a lungo raggio è stato attivato e l’eccitazione globale è stata correttamente bilanciata con l’inibizione locale, l’esponente era più vicino all’esponente della fMRI empirica(Figura 7-figure supplement 2).Qui, l’accoppiamento globale e un singolo valore per tutti i parametri di connessione locale inibitoriaJi sono stati sintonizzati. I colori indicano le correlazioni medie tra i dati simulati ed empirici(a-c) e la differenza assoluta tra gli esponenti della legge di potenza si adatta con le densità spettrali di potenza empiriche e simulate (d, la colormap è stata capovolta per indicare i più alti si adatta in rosso per essere coerente con le altre sottotrame), mediati su tutte le regioni.

Video 1.Elaborazione di informazioni neurali di ingegneria inversa.Il video mostra come i modelli di rete cerebrale computazionale sono costruiti a partire da dati di neuroimaging individuale, come questi modelli possono essere utilizzati per simulare diversi tipi di attività neurale di singoli soggetti su più scale temporali e come l’attività del modello può essere utilizzata per derivare meccanismi di funzione cerebrale.
Gli studi fMRI a riposo hanno identificato le cosiddette “reti a riposo” (RSN), che sono reti diffuse di attività coerente che emergono spontaneamente attraverso una varietà di specie in assenza di un compito esplicito (Biswalet al., 1995; Fox e Raichle, 2007; Raichle et al., 2001). Nonostante le correlazioni tra fMRI e registrazioni intracorticali(He et al., 2008; Logothetis et al., 2001), EEG(Becker et al., 2011; Goldman et al., 2002; Mantini et al., 2007; Moosmann et al., 2003; Ritter et al., 2009) e magnetoencefalografia(Brookes et al., 2011; de Pasquale et al., 2010) il legame tra RSN e attività neurale elettrica non è pienamente compreso. Una caratteristica importante dell’attività neurale elettrica sono le oscillazioni nella banda α, che è l’attività ritmica nella gamma di frequenza da 8 a 12 Hz scoperta per la prima volta da Hans Berger (Berger, 1929). Un corpo crescente di ricerca indica che i cambiamenti nel trattamento delle informazioni, l’attenzione, la consapevolezza percettiva, e le prestazioni cognitive sono accompagnati da una modulazione ritmica di α-potenza e fase (Buschet al., 2009; Klimesch , 1999; Mathewson et al., 2009). La relazione inversa osservata tra l’attività della α-banda e la cottura neurale è centrale nelle ipotesi sul suo significato funzionale definito ‘gating by inhibition’ e ‘pulsed inhibition’ (Jensen e Mazaheri,2010; Klimesch et al., 2007 ). È interessante notare che le registrazioni intracellulari hanno mostrato che gli eventi inibitori sono inseparabili dagli eventi eccitatori, con il risultato di un continuo equilibrio eccitazione-inibizione (equilibrio E/I)(Isaacson e Scanziani, 2011; Okun e Lampl, 2008). L’importanza dell’α-ritmo è sottolineata da forti correlazioni negative tra la fluttuazione di potenza della banda α in corso e la fluttuazione di ampiezza della fMRI a riposo (de Muncket al., 2008; Feige et al., 2005; Goldman et al., 2002; Moosmann et al., 2003). Infine, nonostante l’ampio interesse per le dinamiche critiche(Bak, 2013), non sono chiari i fattori determinanti della scala di potenza emergente, un modello di segnale onnipresente in natura e comunemente osservato nell’attività neurale(Beggs e Timme, 2012; Marković e Gros, 2014).
Per illustrare il potenziale di questo quadro di riferimento per l’inferenza dei processi neurofisiologici, mostriamo i meccanismi dedotti per tre diversi fenomeni empirici e come essi si relazionano ad altri modelli di segnale neurale ben consolidati(Figura 2). Dopo aver scoperto che il modello ibrido predice l’attività fMRI, abbiamo cercato di identificare come l’EEG iniettato ha guidato la previsione delle serie temporali fMRI specifiche del soggetto. L’analisi ci ha portato ad un meccanismo che ha trasformato le fluttuazioni di potenza α dell’attività della sorgente EEG iniettata in oscillazioni fMRI. Il meccanismo identificato può spiegare la correlazione empiricamente osservata tra EEG e fMRI sulla scala temporale più lunga delle oscillazioni fMRI lente. Di conseguenza, abbiamo chiesto come l’effetto inibitorio dell’aumento della potenza della banda α sia stato creato sulla scala temporale più veloce delle fluttuazioni α-fase. L’analisi ci ha portato all’identificazione di un effetto inibitorio risultante dall’interazione tra le oscillazioni di corrente postsinaptiche e i circuiti della popolazione locale. È interessante notare che l’esplorazione spaziale dei parametri ha mostrato che la qualità della previsione è diminuita quando l’accoppiamento a lungo raggio è stato disattivato (cioè quando i nodi della rete a lungo raggio sono stati isolati l’uno dall’altro). Pertanto, abbiamo interrogato il modello per l’influenza dell’accoppiamento strutturale sull’emergere delle oscillazioni fMRI e abbiamo trovato che l’accoppiamento globale amplificava le oscillazioni cerebrali in modo dipendente dalla frequenza, amplificando le oscillazioni più lente più che quelle più veloci, il che facilitava l’emergere di una scalatura di potenza. Partendo dagli effetti della scala temporale veloce, il nostro primo risultato del modello spiega la relazione inversa osservata in modo invasivo tra la fase di picco e la fase α-ritmo, identificando un meccanismo che mette in relazione questo fenomeno con l’equilibrio E/I in corso. Il secondo risultato del modello pone un’origine neurale delle oscillazioni dell’RSN fMRI identificando un meccanismo esplicito che trasforma le fluttuazioni α-potenza in corso in oscillazioni fMRI lente, il che spiega anche le anti-correlazioni empiricamente osservate tra le serie temporali α-potenza e fMRI. Il nostro terzo risultato del modello indica che l’invarianza di scala degli spettri di potenza fMRI risulta dall’auto-rinforzamento dell’eccitazione di feedback attraverso la connettività strutturale a lungo raggio, che porta all’amplificazione delle oscillazioni neurali in funzione della frequenza.
In sintesi, il nostro modello cerebrale biofisicamente fondato ha il potenziale per testare ipotesi meccanicistiche su fenomeni emergenti come la dinamica senza scala, il ruolo cruciale dell’equilibrio eccitazione-inibizione e i correlati emodinamici dell’attività α. Tuttavia, c’è un’altra prospettiva su questa forma di modellazione ibrida. Poiché utilizza dati EEG empirici per generare previsioni di risposte fMRI, può essere considerata una forma di fusione multimodale sotto un modello generativo che è sia fisiologicamente che anatomicamente fondato. Inoltre, poiché utilizziamo vincoli di connettività basati sulla tractografia, serve anche a fondere i dati strutturali con quelli funzionali.

Figura 1.Struttura di modellazione ibrida.I modelli di rete cerebrale ibrida sono costruiti a partire da tractografia a risonanza magnetica ponderata per diffusione e da parcelle regionali ottenute da risonanza magnetica anatomica. I nodi dei modelli ibridi sono iniettati con le serie temporali di attività della sorgente EEG specifica del soggetto invece del rumore. Le serie temporali fMRI previste sono adatte alle serie temporali empiriche fMRI di ciascun soggetto, che sono state acquisite simultaneamente con l’EEG. Ad ogni nodo (piccoli cerchi rossi) della rete a lungo raggio (linee verdi) sono reti locali di modelli di popolazione neurali eccitatori (E) e inibitori(I) che sono guidati dall’attività della sorgente EEG (frecce rosse). I nodi sono globalmente accoppiati da connettimi strutturali (frecce verdi) che rappresentano l’eterogenea forza di accoppiamento della materia bianca tra le diverse aree cerebrali. Correnti sinaptiche di ingresso(equazioni 1 e 2), velocità di scatto(equazioni 3 e 4 ) e attività sinaptica (equazioni5 e 6) alla base delle previsioni fMRI sono analizzati per identificare come l’attività della popolazione neurale e le interazioni di rete si riferiscono a segnali di neuroimaging osservabili. Vedi anche Video 1 per una visualizzazione della costruzione del modello di rete cerebrale e dei risultati esemplari di simulazioni di modelli ibridi.

Figura 2.Figura 2. Panoramica di sei fenomeni empirici su diverse scale temporali riprodotti dal modello ibrido.(a) Il fuoco dei neuroni è inversamente correlato alla fase delle onde α: durante i picchi delle onde α, i neuroni sparano il minimo, mentre sparano il massimo durante i trogoli (adattato da Haegens et al., 2011).(b) Le nostre simulazioni indicano che la relazione inversa tra lo sparo e la fase α è legata al continuo bilanciamento dell’eccitazione e dell’inibizione neurale (adattato da Atallah e Scanziani, 2009). Ristampato con il permesso di Elsevier).(c) Su una scala temporale più lunga (<0,25 Hz), le oscillazioni delle velocità di sparo sono inversamente correlate alle fluttuazioni di potenza in banda α (adattato da Haegens et al., 2011).(d) Le simulazioni del modello suggeriscono un meccanismo che trasforma le oscillazioni di potenza in banda α in oscillazioni fMRI, prevedendo serie temporali fMRI a riposo specifiche del soggetto, modelli di rete spaziale corrispondenti e la correlazione inversa tra α-potenza e fMRI (adattato da de Munck et al., 2008. Ristampato con il permesso di Elsevier.).e) L’emergere di spettri di potenza fMRI senza scala (adattato da He, 2011) è il risultato di un input di rete a lungo raggio.(f) Sono state previste matrici di connettività funzionali individuali su finestre di tempo lunghe e brevi (adattato da Allen et al., 2014).

Figura 3-figure supplement 1.Figura 3—supplemento alla figura 1. Predizione delle serie temporali fMRI specifiche per la persona.a) Serie temporali esemplificative del modello ibrido e dei tre scenari di controllo di un soggetto.(b) Box plot di coefficienti di correlazione medi tra tutte le serie temporali simulate e le regioni empiriche (20,7 min) per ogni soggetto (n = 15; i valori di α-regressor sono stati invertiti a scopo illustrativo).c) Diagramma di dispersione della deviazione standard del corso del tempo RSN (s.d.) rispetto alla qualità della previsione. I punti rappresentano i dati dei nove corsi di tempo RSN per ogni soggetto.d) Confronto della qualità di previsione durante il quartile superiore e inferiore del corso temporale dell’RSN epocale s.d.s. Riga superiore: modelli di attivazione spaziale di nove RSN. Fila centrale: coefficienti di correlazione tra i modi temporali di RSN e i risultati della simulazione del modello ibrido e i tre scenari di controllo. Fila inferiore: finestra scorrevole (lunghezza: 100 scansioni fMRI = 194 s; larghezza del passo: una scansione fMRI) correlazioni per le correlazioni dei quartili superiori (primo e terzo boxplot per pannello) e inferiori (secondo e quarto boxplot per pannello) della modalità temporale RSN a finestra per il modello ibrido e il regressore α. Gli asterischi indicano un significativo aumento della qualità di previsione del modello ibrido rispetto agli scenari di controllo nel test di somma del rango Wilcoxon a una coda (*p<0,05, **p<0,01). Inoltre, tutte le correlazioni del modello ibrido in(b) e(d) sono state testate per l’ipotesi nulla che provengano da una distribuzione la cui mediana è pari a zero al livello di significatività del 5%. Tutti i test hanno respinto l’ipotesi nulla delle mediane zero, ad eccezione delle correlazioni RSN su 20 minuti per il controllo esecutivo e le reti frontoparietali (riga centrale).(a-c) 2d parametro mappe di calore spaziale parametro2d mostrano la correlazione media delle serie temporali ottenuti dal modello ibrido per diverse combinazioni dei tre parametri G, ω BGE, ω BGI (quest’ultimoraffigurato come rapporto ω BGI / ω BGE),i risultati sono stati mediati su tutti i soggetti e le regioni cerebrali. I valori dei parametri che hanno prodotto la più alta correlazione media sono stati utilizzati per le simulazioni con l’ingresso artificiale α (contrassegnato con un asterisco). Abbiamo confermato l’identificabilità del modello mostrando che la ricerca dello spazio dei parametri converge verso un’unica soluzione ottimale che fornisce le migliori previsioni.

Figura 3-figure supplemento 1.Risultati dell’esplorazione dello spazio con i parametri.(a-c) Le mappe del calore dello spazio con il parametro2d mostrano la correlazione media delle serie temporali ottenute dal modello ibrido per diverse combinazioni dei tre parametri G, ω BGE, ω BGI (quest’ultimorappresentato come rapporto ω BGI / ω BGE); irisultati sono stati mediati su tutti i soggetti e le regioni cerebrali. I valori dei parametri che hanno prodotto la più alta correlazione media sono stati utilizzati per le simulazioni con l’ingresso artificiale α (contrassegnato con un asterisco). Abbiamo confermato l’identificabilità del modello mostrando che la ricerca dello spazio dei parametri converge verso un’unica soluzione ottimale che fornisce le migliori previsioni.

Figura 4.Previsione funzionale della connettività.(a, b) I diagrammi di box mostrano i coefficienti di correlazione ottenuti dalla correlazione di tutte le voci sottodiagonali delle matrici FC empiriche e simulate. FC è stato calcolato per le epoche lunghe (FC statico; calcolato su 20,7 min) e per le epoche brevi (FC dinamico; correlazione finestra scorrevole media; 100 scansioni fMRI lunghezza finestra; una scansione fMRI larghezza passo passo). I risultati sono stati confrontati per(a) il set di parametri che ha generato la migliore previsione delle serie temporali fMRI e(b) il set di parametri che ha prodotto le migliori previsioni FC per ogni soggetto.c) I diagrammi di dispersione confrontano la media FC empirica e quella simulata per le simulazioni di modelli ibridi e il regressore α. I punti rappresentano tutte le correlazioni delle serie temporali delle regioni a coppie in media su tutti i soggetti. Gli asterischi in(a) e(b) indicano una qualità di previsione significativamente aumentata del modello ibrido rispetto alle condizioni di controllo nel test di somma del rango Wilcoxon a una coda (*p<0.05, **p<0.01).

Figura 5.L’equilibrio E/I genera la relazione inversa tra la fase α e la cottura.a) Istogramma dei tassi di cottura della popolazione diviso in sei contenitori secondo i segmenti del ciclo α e normalizzato rispetto al tasso medio di cottura di ogni ciclo. I tassi di cottura della popolazione erano più alti durante la depressione e più bassi durante il picco di α-cicli.b) Grande media delle forme d’onda delle entrate e delle uscite della popolazione bloccata al tempo di α-cicli di attività della sorgente EEG iniettata (nero, colonna II). Gli assi destro e sinistro indicano rispettivamente le correnti in ingresso alle popolazioni eccitatorie e inibitorie. Si prega di fare riferimento al testo principale per una descrizione del meccanismo che spiega la relazione inversa tra α-cicli e velocità di accensione.

Figura 6-figure supplemento 1.α-potenza fluttuazioni generano oscillazioni fMRI.α-potenza prevede il tasso di cottura.Grande media delle forme d’onda degli ingressi e delle uscite della popolazione su scale temporali più lunghe.(a) I modelli ibridi sono stati iniettati con α-attività artificiale che consiste di oscillazioni sinusoidali a 10 Hz che contengono un singolo breve scoppio ad alta potenza (nero, colonna I; arancione: inviluppo del segnale). Mentre le deflessioni positive dell’onda α generavano deflessioni positive dei tassi di cottura della popolazione inibitoria, grandi deflessioni negative erano delimitate dal vincolo fisiologico di 0 Hz (blu, quinta colonna; nero: media mobile).b) I modelli ibridi sono stati iniettati modelli con onde sinusoidali a 10 Hz dove la potenza in corso è stata modulata in modo simile a α-ritmi empirici (0,01-0,03 Hz). Analogamente a(a), ma per un periodo di tempo più lungo, popolazioni inibitorie rettificato deflessioni negative, che ha introdotto l’α-potenza modulazione come una nuova componente di frequenza come una nuova componente di frequenza in tassi di cottura e serie temporali fMRI.Analogamente ai risultati elettrofisiologici mostrati in Haegens et al. (2011), tutte le serie temporali per ogni soggetto e regione cerebrale sono state divise in cinque contenitori di uguali dimensioni sulla base del livello di potenza α e del tasso di cottura medio (normalizzato con il tasso di cottura medio per regione cerebrale) è stato calcolato per contenitore. Il tasso di cottura è diminuito con l’aumento di α-potenza (Kruskal-Wallis/Tukey post-hoc confronto multiplo; p<0,001).

Figura 6-figure supplemento 1.α-potenza prevede la velocità di sparo.Analogamente ai risultati elettrofisiologici mostrati in Haegens et al. (2011), tutte le serie temporali per ogni soggetto e regione cerebrale sono state suddivise in cinque contenitori di uguali dimensioni sulla base del livello di potenza α e del tasso di cottura medio (normalizzato con il tasso di cottura medio per regione cerebrale) è stato calcolato per contenitore. Il tasso di cottura è diminuito con l’aumento di α-potenza (Kruskal-Wallis/Tukey post-hoc confronto multiplo; p<0,001).

Figura 7-figure supplemento 2.Come nella Figura 7a, ma le simulazioni sono state eseguite con il modello ibrido semplificato, cioè i modelli non hanno utilizzato alcun controllo di inibizione di feedback (FIC) e un unico valore per tutte le connessioni locali inibitorie Ji è stato utilizzato.(a) Densità spettrali di potenza di fMRI simulata ed empirica e attività empirica in banda α (gli adattamenti in linea retta degli spettri di potenza sono solo a scopo illustrativo; l’invarianza di scala è stata determinata nel dominio del tempo utilizzando rigorosi criteri di selezione del modello, vedi Materiali e metodi).b) Come nella Figura 6b, ma con accoppiamento a lungo raggio disabilitato. In contrasto con la Figura 6b, le ampiezze dei tassi di cottura, gating sinaptico e fMRI sono ugualmente grandi, mentre nella Figura 6b le ampiezze erano più grandi durante le modulazioni di potenza in banda α più lente.Gli spettri fMRI empirici e simulati hanno un grande esponente della legge di potenza, cioè una pendenza più ripida, rispetto alla potenza α-potenza in corso o alla potenza a banda larga (β α-banda = -0,53, β banda larga = -0,47). Per analizzare l’effetto dell’interazione di rete a lungo raggio, la fMRI simulata è stata calcolata con e senza accoppiamento a lungo raggio. Per escludere che gli spettri di potenza emergano nonostante l’assenza dell’accoppiamento a lungo raggio, l’inibizione locale è stata regolata in modo tale che il modello producesse le più alte previsioni delle serie temporali fMRI. Senza l’accoppiamento a lungo raggio, la fMRI simulata ha mostrato un esponente simile all’attività della sorgente EEG iniettata. Quando l’accoppiamento a lungo raggio è stato attivato e l’eccitazione globale è stata correttamente bilanciata con l’inibizione locale, l’esponente era più vicino all’esponente della fMRI empirica(Figura 7-figure supplement 2).Qui, l’accoppiamento globale e un singolo valore per tutti i parametri di connessione locale inibitoriaJi sono stati sintonizzati. I colori indicano le correlazioni medie tra i dati simulati ed empirici(a-c) e la differenza assoluta tra gli esponenti della legge di potenza si adatta con le densità spettrali di potenza empiriche e simulate (d, la colormap è stata capovolta per indicare i più alti si adatta in rosso per essere coerente con le altre sottotrame), mediati su tutte le regioni.
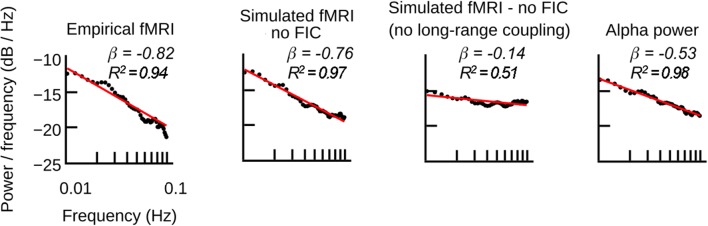
Figura 7-figure supplement 1.Come nella Figura 7a, ma le simulazioni sono state eseguite con il modello ibrido semplificato, cioè i modelli non utilizzavano il controllo dell’inibizione di feedback (FIC) ed è stato utilizzato un unico valore per tutte le connessioni inibitorie locali Ji.Gli spettri fMRI empirici e simulati hanno un grande esponente di potenza, cioè una pendenza più ripida, rispetto alla potenza α-potenza in corso o alla potenza a banda larga (β α-banda = -0,53, β banda larga = -0,47). Per analizzare l’effetto dell’interazione di rete a lungo raggio, la fMRI simulata è stata calcolata con e senza accoppiamento a lungo raggio. Per escludere che gli spettri di potenza emergano nonostante l’assenza dell’accoppiamento a lungo raggio, l’inibizione locale è stata regolata in modo tale che il modello producesse le più alte previsioni delle serie temporali fMRI. Senza l’accoppiamento a lungo raggio, la fMRI simulata ha mostrato un esponente simile all’attività della sorgente EEG iniettata. Quando l’accoppiamento a lungo raggio è stato attivato e l’eccitazione globale è stata correttamente bilanciata con l’inibizione locale, l’esponente era più vicino all’esponente della fMRI empirica(Figura 7-figure supplement 2).

Figura 7-figure supplemento 2.Esplorazione spaziale a grana fine del modello ibrido semplificato per un soggetto esemplare.Qui, l’accoppiamento globale e un unico valore per tutti i parametri di connessione locale inibitoriaJi sono stati sintonizzati. I colori indicano le correlazioni medie tra i dati simulati ed empirici(a-c) e la differenza assoluta tra gli esponenti della legge di potenza si adatta con le densità spettrali di potenza empiriche e simulate (d, la colormap è stata capovolta per indicare i più alti si adatta in rosso per essere coerente con le altre sottotrame), mediati su tutte le regioni.

Video 1.Elaborazione di informazioni neurali di ingegneria inversa.Il video mostra come i modelli di rete cerebrale computazionale sono costruiti a partire da dati di neuroimaging individuale, come questi modelli possono essere utilizzati per simulare diversi tipi di attività neurale di singoli soggetti su più scale temporali e come l’attività del modello può essere utilizzata per derivare meccanismi di funzione cerebrale.
Risultati
I modelli ibridi prevedono serie temporali fMRI specifiche del soggetto
I modelli di rete cerebrale utilizzati sono sistemi dinamici in cui le singole aree cerebrali sono simulate da modelli di massa neurale accoppiati. L’accoppiamento a lungo raggio è stato ponderato con stime di forza eterogenee ottenute dalla tractografia in materia bianca, un metodo che stima i tratti neurali dai dati di risonanza magnetica ponderati per diffusione. I modelli di massa neurale utilizzati approssimano il comportamento medio d’insieme delle reti di modelli neuronali di spiking e sono stati derivati in un precedente studio(Deco et al., 2013) utilizzando una tecnica di campo medio dinamico(Deco et al., 2008; Wong e Wang, 2006). A differenza dei precedenti modelli di reti cerebrali che utilizzavano il rumore come input, i modelli di massa neurale del nostro modello ‘ibrido’ sono guidati dall’attività della sorgente EEG che è stata acquisita simultaneamente con la fMRI (Figura 1). I risultati della simulazione hanno previsto una parte considerevole della varianza delle serie temporali fMRI a riposo specifiche del soggetto in corso(Figura 3) e delle topologie di rete spaziale, cioè la connettività funzionale fMRI(Figura 4; la connettività funzionale è qui definita come la matrice di correlazione di coppia tra le serie temporali della regione). Inoltre, i modelli montati hanno riprodotto una varietà di fenomeni empirici osservati con l’EEG e l’elettrofisiologia invasiva(Figura 2) e, cosa più importante, i risultati della simulazione hanno rivelato spiegazioni meccanicistiche per l’emergere di questi fenomeni(Figure 5, 6 e 7).
Abbiamo costruito modelli di reti cerebrali ibride individuali per 15 soggetti umani adulti utilizzando i propri connettori strutturali di ogni soggetto e iniettato ciascuno con i propri corsi di tempo di attività di origine EEG a livello regionale che sono stati acquisiti contemporaneamente ai dati fMRI successivamente previsti. Utilizzando ricerche esaustive, abbiamo sintonizzato tre parametri globali per ciascuno dei 15 singoli modelli di rete cerebrale ibrida individuale per produrre la più alta misura tra ciascuna delle regioni empiriche del soggetto – serie temporali fMRI media regione e corrispondenti serie temporali simulate (Figura 3-figure supplemento 1). La nostra motivazione per la scelta di quel set di parametri che ha prodotto la più alta correlazione tra le serie temporali fMRI simulate ed empiriche si basa sul nostro obiettivo di dedurre le dinamiche e i parametri sottostanti (ma non osservabili) del sistema reale. Questa idea si basa sul presupposto che quando il modello si adatta in modo ottimale all’attività cerebrale osservabile, allora anche l’attività cerebrale sottostante non osservabile viene riprodotta fedelmente. Il primo parametro scala la forza globale dell’accoppiamento a lungo raggio tra le regioni. Il secondo e il terzo parametro scala i punti di forza degli input di attività di origine EEG iniettati nelle popolazioni eccitatorie e inibitorie, rispettivamente. Per valutare meglio la qualità delle previsioni fMRI, abbiamo confrontato i risultati del modello ibrido con tre scenari di controllo: (i) il modello originale di rete cerebrale basato sul rumore, (ii) una variante del modello ibrido in cui le fasi temporali delle serie temporali dell’attività della sorgente EEG iniettata erano permutati in modo casuale e (iii) un modello statistico in cui la fluttuazione di potenza della banda α in corso dell’attività della sorgente EEG iniettata era contorta con la funzione di risposta emodinamica canonica (d’ora in poi chiamata α-regressor). I primi due controlli sono modelli di rete cerebrale e il terzo si ispira alle analisi tradizionali dei dati empirici EEG-fMRI. I controlli servono ad escludere che le correlazioni ottenute tra fMRI simulata ed empirica siano un risultato banale che verrebbe prodotto anche dal modello originale basato sul rumore o con serie temporali di input casuali.
L’esame visivo delle serie temporali di esempio ha mostrato una buona riproduzione delle oscillazioni caratteristiche lente (<0,1 Hz) dell’RSN da parte del modello ibrido e dell’α-regressor (anche se invertito per quest’ultimo), ma una scarsa riproduzione della dinamica temporale nel caso di modelli di rumore e permutazioni casuali (Figura 3). Abbiamo confrontato i coefficienti di correlazione medi tra tutte le serie temporali fMRI simulate ed empiriche tra tutti e quattro gli scenari (cioè il modello ibrido e le tre configurazioni di controllo). Le previsioni del modello ibrido hanno correlato significativamente meglio con le serie temporali fMRI empiriche rispetto alle previsioni dei due modelli casuali e del regressore α (Figura 3b). Per il modello ibrido, la validazione incrociata di cinque volte non ha mostrato alcuna differenza significativa di qualità di previsione tra le serie di dati di addestramento e di validazione (test di somma a due code del rango Wilcoxon, p=0,71, t= 0.54, delta d di Cliff = 0,0044) e tra i set di dati di validazione e la qualità di previsione per le serie a tempo pieno (test di somma del rango Wilcoxon a due code, p=0,42, t = -0,2, delta d di Cliff= -0,067).
Per stimare la capacità dei quattro scenari di prevedere i percorsi temporali dei diversi RSN comunemente osservati abbiamo eseguito un’analisi spaziale indipendente dei componenti (ICA) a livello di gruppo dei dati empirici fMRI. Successivamente, abbiamo calcolato i coefficienti di correlazione medi tra ciascun corso temporale di RSN specifico del soggetto e le regioni del modello nella posizione del rispettivo RSN. Come nel caso della fMRI a livello regionale(Figura 3b), i coefficienti di correlazione del modello ibrido erano significativamente più grandi dei modelli di rete di controllo per la maggior parte delle RSN(Figura 3d). Le analisi a finestra scorrevole hanno mostrato che la qualità della previsione variava nel tempo, nelle regioni e nei soggetti: la qualità della previsione a finestra era altamente correlata con la deviazione standard delle modalità temporali RSN(Figura 3c,d). Cioè, maggiore è la varianza che ha contribuito all’attività complessiva della fMRI da parte di un RSN in un dato soggetto e in una data finestra temporale, migliore è la previsione della fMRI empirica, che potrebbe riflettere una maggiore sincronia dell’attività elettrica (vedi Discussione). Di conseguenza, le epoche nel quartile superiore di RSN s.d.s. sono state significativamente meglio previste rispetto alle epoche nel quartile inferiore(Figura 3d). Al fine di valutare la specificità del soggetto – la specificità delle previsioni delle serie temporali fMRI, abbiamo correlato tutti i risultati della simulazione (cioè per ogni soggetto e per ogni combinazione di parametri testata) anche con l’attività empirica fMRI di tutti gli altri soggetti. Abbiamo trovato che i coefficienti di correlazione massimi su tutti i parametri testati erano significativamente più grandi quando le serie di dati empirici e simulati appartenevano allo stesso soggetto rispetto a quando provenivano da soggetti diversi (p<<0,01, test della somma di Wilcoxon rank sum).
Successivamente, abbiamo confrontato la capacità di tutte e quattro le configurazioni di prevedere la topologia spaziale delle reti fMRI empiriche. In contrasto con la previsione di serie temporali, l’α-regressor ha mostrato basse correlazioni con la connettività funzionale empirica (FC). Rispetto al α-regressor, tutti e tre gli approcci basati su modelli hanno fornito previsioni significativamente migliori dei soggetti individuali a lungo e a breve termine FC (Figura 4). Inoltre, i risultati della simulazione del modello ibrido sono correlati in modo significativamente migliore con la topologia di rete empirica rispetto alle previsioni ottenute dal modello basato sul rumore(Figura 4a,b). È interessante notare che le correlazioni per i modelli di permutazione ibrida e casuale erano effettivamente le stesse, probabilmente perché le dinamiche di rete a lungo raggio, che guidano l’emergere di FC attraverso l’accoppiamento strutturale, sarebbero relativamente preservate quando permutano l’attività iniettata. La previsione della FC media di gruppo (tutti i valori di FC a coppie mediate su tutti i soggetti) è stata migliore per il modello ibrido rispetto all’α-regressor (Figura 4c).
E / I equilibrio genera la relazione inversa tra α-fase e la cottura
Dopo aver adattato i singoli modelli ibridi per ciascuno dei 15 soggetti, abbiamo analizzato l’attività della popolazione locale per dedurre i meccanismi neurodinamici alla base delle serie temporali previste della fMRI. Abbiamo trovato che sulla scala temporale veloce dei singoli α-cicli individuali (~ 100 ms) il modello ibrido ottimizzato riproduceva la relazione inversa tra la fase α e i tassi di cottura osservati nelle registrazioni invasive (Haegens etal., 2011) (Figura 5a). Per indagare queste dinamiche ad azione rapida relative alla fase α, abbiamo calcolato la grande media delle forme d’onda degli ingressi sinaptici modellati, i tassi di cottura della popolazione e il gating sinaptico bloccato nel tempo agli incroci zero di α-cicli. Le forme d’onda risultanti illustrano come il continuo bilanciamento degli input eccitatori e inibitori abbia generato la relazione inversa tra α-oscillazioni e cottura neurale (Figura 5b).
Nei modelli ibridi, l’attività della sorgente del singolo soggetto (Figura 5, colonna I) (colonna II) è utilizzata come un’approssimazione di EPSC (colonna III). Come risultato dell’ottimizzazione dei tre parametri del modello, gli EPSCs hanno dominato la somma della corrente di ingresso sinaptica per inibire le popolazioni inibitorie (colonna IV). Di conseguenza, le popolazioni inibitorie (colonna V) hanno seguito da vicino la forma degli EPSC (colonna VI) e il gating sinaptico (colonna VII). A causa della relazione monotona tra le correnti in ingresso e le velocità di sparo in uscita (definite dall’equazione 3 e 4), anche la forma d’onda delle velocità di sparo inibitorie e del gating sinaptico ha seguito da vicino la forma delle EPSC iniettate. Poiché l’aumento dell’input alle popolazioni inibitorie porta ad un aumento dell’effetto inibitorio e viceversa, le forme d’onda di inibizione di feedback (IPSC, colonna III) sono state invertite alle EPSC. Inoltre, la fluttuazione di ampiezza degli EPSC e degli IPSC è stata proporzionale. Cioè, gli EPSC più forti hanno preceduto e contribuito a generare IPSC più forti. In altre parole, l’eccitazione e l’inibizione sono state bilanciate durante ogni ciclo, il che è in accordo con i risultati elettrofisiologici pubblicati(Haider et al., 2016; Isaacson e Scanziani, 2011; Okun e Lampl, 2008; Xue et al., 2014). Di conseguenza, gli IPSC hanno raggiunto il picco massimo durante la depressione della fase α e sono stati più bassi durante il picco della fase α. L’adattamento dei modelli all’attività fMRI ha portato a un rapporto biologicamente plausibile tra EPSC e IPSC(Xue et al., 2014), con ampiezze di IPSC circa tre volte superiori alle ampiezze di EPSC (confrontare gli assi sinistri delle trame di EPSC e IPSC). Poiché gli IPSC hanno dominato gli input della popolazione eccitatoria, i tassi di cottura delle popolazioni eccitatorie hanno mostrato una forma simile a quella degli IPSC, ovvero hanno raggiunto il picco massimo durante il ciclo α e sono scesi al minimo durante il picco del ciclo α, riproducendo così la relazione empirica tra il ciclo α e il tasso di cottura (Haegens et al.,2011). Le colonne IV, VI e VII si riferiscono rispettivamente alle equazioni 1, 3 e 5 (popolazione eccitatoria) e 2, 4 e 6 (popolazione inibitoria).
In sintesi, l’attività di popolazione veloce alla base delle previsioni della fMRI ha mostrato una modulazione ritmica dei tassi di cottura sulla scala temporale veloce dei singoli α-cicli in accordo con le osservazioni empiriche (Haegenset al., 2011). Le analisi hanno rivelato che gli stati di eccitazione e inibizione che si alternano periodicamente sono il risultato del bilanciamento in corso di EPSCs da feedback IPSCs, che spiega la cottura neurale α-fase-correlata.
α- fluttuazioni di potenza generano oscillazioni fMRI
Simile alle registrazioni intracraniche in scimmia(Haegens et al., 2011), abbiamo trovato che l’aumento della potenza α dell’attività della sorgente EEG iniettata è stato accompagnato da una diminuzione dei tassi di cottura (Figura 6-figure supplement 1). Inoltre, abbiamo anche osservato la relazione inversa empiricamente osservata tra α-potenza e ampiezza fMRI (Goldmanet al., 2002; Moosmann et al., 2003) nei nostri dati empirici sotto forma di correlazioni negative tra il regressore α e l’attività fMRI (Figura 3). I nostri risultati hanno sollevato la questione di quale meccanismo fisiologico ha portato a questa relazione inversa tra α-potenza e velocità di sparo, rispettivamente, l’ampiezza fMRI. Abbiamo quindi analizzato l’attività del modello su una scala temporale più lunga di fluttuazioni di potenza α. Per isolare gli effetti delle onde α da altri ritmi EEG, abbiamo sostituito l’attività di fonte EEG iniettata nei 15 singoli modelli ibridi con α-attività artificiale (Figura 6a,colonna I) e simulato tutti i 15 modelli ibridi utilizzando il singolo set di parametri che in precedenza ha generato la più alta qualità media di previsione delle serie temporali fMRI (Figura 3-figuresupplemento 1). L’attività iniettata consisteva in un’onda sinusoidale di 10 Hz che conteneva un singolo breve breve scoppio ad alta potenza nel suo centro, al fine di consentire all’attività del modello di stabilizzarsi per fasi sufficientemente lunghe prima e dopo lo scoppio ad alta potenza. Dopo la simulazione, abbiamo calcolato la grande media delle forme d’onda delle variabili dello stato del modello su tutte le serie temporali della regione simulata e abbiamo scoperto che le correnti di ingresso, i tassi di accensione, l’attività sinaptica e l’attività fMRI delle popolazioni eccitatorie sono diminuite in risposta al α-burst (Figura 6a). In particolare, questo comportamento è emerso nonostante il fatto che l’attività iniettata (colonna I) fosse centrata a zero, cioè le deviazioni positive e negative delle correnti di ingresso erano bilanciate. La ragione della risposta asimmetrica osservata all’aumento dei livelli di potenza α in ingresso ha avuto origine dalla dinamica della popolazione inibitoria: mentre le deflessioni positive dei cicli α hanno generato grandi picchi nei tassi di cottura in corso delle popolazioni inibitorie, le deflessioni negative sono state delimitate da 0 Hz (colonna V). A causa di questa rettifica dei semicicli negativi ad alta ampiezza, i tassi medi di cottura per ciclo delle popolazioni inibitorie sono aumentati con l’aumentare della potenza α. Di conseguenza, anche l’inibizione di feedback (IPSC, colonna II) era aumentato per l’aumento di α-potenza, che a sua volta ha portato ad una maggiore inibizione delle popolazioni eccitatorie, diminuzione dei tassi medi di cottura, variabili di gating sinaptiche (colonna VI) e, infine, le ampiezze fMRI (colonna VII).
Abbiamo poi analizzato la relazione tra le fluttuazioni di potenza α e le oscillazioni della fMRI. Abbiamo generato artificiale α-attività costituito da un’onda sinusoidale di 10 Hz che è stata modulata in ampiezza da oscillazioni lente (frequenze di ciclo tra 0,01 e 0,03 Hz) e iniettato nei modelli ibridi di tutti i soggetti (Figura 6b, colonna I). Come nell’esempio precedente, le popolazioni inibitorie hanno filtrato le α-deflessioni negative durante le epoche di maggiore potenza (colonna V). Questa rettifica a mezza onda ha portato ad una modulazione dei tassi medi di cottura per ciclo in proporzione alla potenza α. Di conseguenza, la modulazione di potenza della α-oscillazione iniettata è stata introdotta come nuova componente di frequenza lenta nelle serie temporali risultanti. L’attività delle popolazioni inibitorie può essere paragonata al rilevamento dell’inviluppo utilizzato nella comunicazione radio per la demodulazione del segnale AM. La nuova componente di frequenza introdotta dalla rettifica a mezza onda di α-attività modulata di inibizione di feedback (IPSC, colonna II), che a sua volta modulato tassi di cottura eccitatori popolazione eccitatori (colonna V). Inoltre, l’oscillazione risultante dei tassi di cottura è stata propagata alla dinamica sinaptica (colonna VI), dove la grande costante di tempo di NMDAergic synaptic gating(τNMDANMDA100 ms vs. τGABAGABA10 ms) ha portato ad un’attenuazione delle frequenze più alte. La proprietà di filtraggio passa-basso della risposta emodinamica ha inoltre attenuato le frequenze più alte in modo tale che nei segnali fMRI (colonna VII) sono rimaste solo le componenti di frequenza lenta, sulla base del presupposto che l’accoppiamento neurovascolare era mediato esclusivamente dall’attività sinaptica eccitatoria. Per riaffermare: la fluttuazione di potenza α ha introdotto una modulazione lenta invertita dei tassi di cottura e l’attività sinaptica, le proprietà di filtraggio passa-basso del gating sinaptico e le risposte emodinamiche attenuato frequenze più alte in modo che solo l’oscillazione lenta è rimasto in segnali fMRI. Per verificare se questo meccanismo è robusto per la scelta della frequenza del α-ritmo iniettato (10 Hz) abbiamo simulato modelli altrimenti identici per le onde artificiali α a 9 Hz e 11 Hz frequenze e trovato risultati qualitativamente identici: simulato fMRI e media mobile velocità di cottura serie temporali media del 9 Hz e il modello 11 Hz aveva coefficienti di correlazione r > 0,99 con le rispettive serie temporali del modello 10 Hz.
In sintesi, abbiamo scoperto che l’aumento di α-potenza ha portato ad una maggiore inibizione di feedback delle popolazioni eccitatorie, introducendo una lenta modulazione del tiro della popolazione, che può spiegare l’anticorrelazione empiricamente osservata tra α-potenza e fMRI.
L’accoppiamento a lungo raggio controlla la scala di potenza fMRI
Gli spettri di potenza empirici fMRI seguono una distribuzione di potenza P ∝ f βdove P è potenza, f è frequenza e β l’ esponente della legge sul potere. Secondo le analisi sistematiche dei dati empirici(He, 2011), gli spettri di potenza media dei nostri dati empirici fMRI obbediscono alle distribuzioni di potenza con l’esponente βemp= -0,82 (Figura 7ae Figura 7-figure supplement 1). Abbiamo testato l’esistenza di una scalatura della legge sulla potenza nel dominio del tempo utilizzando rigorosi criteri di selezione del modello che superano i limiti dei semplici adattamenti in linea retta agli spettri di potenza (vedere Materiali e metodi; a scopo illustrativo gli adattamenti in linea retta sono mostrati nella Figura 7a e nella Figura 7-figure supplement 1).
I nostri risultati precedenti hanno associato le oscillazioni fMRI a riposo con l’attività neurale elettrica identificando un meccanismo neurale che trasforma le fluttuazioni di potenza in banda α in oscillazioni fMRI (Figura 6). Questo meccanismo suggerisce che le fluttuazioni di potenza in banda EEG α si trasformano in fluttuazioni di ampiezza fMRI. Pertanto, è sorprendente che gli spettri di potenza dell’EEG a banda larga e dell’EEG a banda α abbiano esponenti negativi notevolmente più piccoli rispetto alla fMRI empirica (βα-band= -0,53 per α-potenza e βbanda larga=-0,47 per la potenza a banda larga). Tuttavia, in accordo con la fMRI empirica, la nostra fMRI simulata aveva un esponente negativo maggiore(βsim= -0,73) rispetto alla potenza della banda α dell’attività della sorgente EEG iniettata (βα-band= −0.53). Questo risultato implica che la pendenza della potenza-legge è aumentata durante il processo che ha trasformato le fluttuazioni elettriche di banda-potenza in fluttuazioni di ampiezza fMRI. Infatti, il confronto degli spettri di potenza ha indicato che la fMRI simulata ha avuto un esponente negativo maggiore rispetto all’attività della sorgente EEG, perché la potenza delle oscillazioni più lente è aumentata rispetto alla potenza delle oscillazioni più veloci(Figura 7a e Figura 7-figure supplement 1). Cioè, la dinamica del modello ha trasformato l’attività sinaptica in ingresso in modo tale che l’ampiezza delle oscillazioni in uscita aumentava inversamente proporzionale alla loro frequenza. È interessante notare che, quando l’accoppiamento a lungo raggio è stato disattivato nelle simulazioni che utilizzavano l’attività della sorgente EEG come input, l’esponente della legge di potenza della fMRI simulata(βsim_Gzero= -0,54) era vicino all’esponente dell’andamento temporale della potenza in banda α dell’attività della sorgente EEG iniettata (βα-band= −0.53). L’effetto è stato visibile anche confrontando le nostre precedenti simulazioni di modelli che utilizzavano l’attività artificiale α (Figura 6b), con le simulazioni in cui l’accoppiamento a lungo raggio è stato disattivato (Figura 7b). Quando l’accoppiamento a lungo raggio è stato disattivato, le ampiezze delle oscillazioni fMRI erano ugualmente grandi per tutte le frequenze di oscillazione(Figura 7b, colonna VII). Al contrario, quando l’accoppiamento a lungo raggio è stato attivato, con tutto il resto essendo identico, le ampiezze delle oscillazioni fMRI più lente erano più grandi delle ampiezze delle oscillazioni più veloci(Figura 6b, colonna VII), anche se le ampiezze delle oscillazioni artificiali iniettate in banda α erano ugualmente grandi per tutte le oscillazioni (Figure6b e 7b, colonna I). Quando era presente l’accoppiamento a lungo raggio, le ampiezze delle oscillazioni lente aumentavano e la relazione tra potenza e frequenza delle oscillazioni si avvicinava all’esponente della legge sulla potenza che si trova negli spettri di potenza empirici fMRI(Figura 7a). Essendo tutto il resto identico, abbiamo concluso che l’accoppiamento a lungo raggio era responsabile dell’aumento della potenza delle oscillazioni più lente rispetto alle oscillazioni più rapide.
Il confronto dei singoli componenti degli ingressi della popolazione per gli ingressi attivati(Figura 6b, colonna II) rispetto a quelli disattivati(Figura 7b, colonna II) ha rafforzato che l’unica differenza negli ingressi della popolazione tra le due configurazioni era la forma dell’ingresso a lungo raggio. Le ampiezze delle oscillazioni di ingresso a lungo raggio(Figura 6b, colonna II, traccia verde) erano inversamente proporzionali all’oscillazione di potenza della banda di oscillazione di α-attività artificiale iniettata. In conformità con l’effetto della potenza in banda α sull’attività della popolazione che abbiamo descritto in precedenza, l’input a lungo raggio è aumentato quando la potenza in banda α è diminuita, mentre durante le epoche di aumento α-attività di accoppiamento a lungo raggio è diminuito. Di conseguenza, questa fluttuazione dell’input a lungo raggio era coerente con la fluttuazione degli IPSC che risultava dalla fluttuazione della potenza della banda α, che amplificava ulteriormente l’effetto della potenza della banda α sull’attività della popolazione. Durante le epoche di bassa α-attività a lungo raggio di accoppiamento a basso α-attività a lungo raggio trasportato l’eccitazione feedforward che ha ulteriormente rafforzato l’aumento di cottura e di gating sinaptico. A causa di questa modulazione consensuale delle correnti in ingresso, le correnti totali in ingresso sono state aumentate quando la potenza della banda α è stata diminuita, il che ha portato ad ampiezze maggiori di velocità di sparo, attività sinaptica e fMRI.
A causa della grande costante di tempo di gating sinaptico eccitatorio (τ NMDA= 100 ms), l’eccitazione a lungo raggio decadde relativamente lentamente, che ha permesso all’attività eccitatoria di accumularsi e di rinforzarsi continuamente all’interno della rete a lungo raggio. Il periodo di tempo per il quale questa eccitazione in feedforward persisteva era più lungo durante le oscillazioni più lente che durante le oscillazioni più veloci. Di conseguenza, l’attività sinaptica (colonna VI) aveva più tempo per accumularsi ed era quindi più grande durante le oscillazioni più lente rispetto alle oscillazioni più veloci. Di conseguenza, le ampiezze di uscita della popolazione eccitatoria (colonne V, VI e VII) hanno raggiunto valori più alti durante le oscillazioni più lente rispetto alle oscillazioni più veloci quando l’accoppiamento a lungo raggio è stato attivato(Figura 6b). Di conseguenza, la potenza delle oscillazioni più lente, e quindi la pendenza dello spettro di potenza, aumenta nel caso di accoppiamento a lungo raggio. Si noti che questo effetto (cioè che le oscillazioni più lente raggiungono ampiezze più elevate) può già essere osservato nelle velocità di accensione e nelle serie temporali di gating sinaptico, il che esclude un’influenza del modello emodinamico in avanti. Al contrario, nel caso di accoppiamento a lungo raggio disattivato(Figura 7b) tutti i picchi di ampiezza sono approssimativamente uguali, che era il risultato atteso, poiché i picchi di ampiezza della modulazione di potenza della modulazione di α-attività iniettata erano ugualmente elevati per costruzione (colonna I, traccia arancione).
Abbiamo chiesto come i punti di forza relativi dell’eccitazione della materia bianca e dell’inibizione della retroazione influenzano la scalatura della potenza. Per testare come l’equilibrio E/I influenza la scalatura della legge di potenza, abbiamo variato la forza dell’accoppiamento a lungo raggio e, anche globalmente, la forza dell’inibizione del feedback. Cioè, a differenza delle nostre precedenti simulazioni, la forza dell’inibizione di retroazione è stata controllata da un singolo parametro per tutte le popolazioni inibitorie. Gli altri parametri, cioè la forza dell’attività della sorgente EEG iniettata nelle popolazioni eccitatorie e inibitorie, sono stati mantenuti fissi. Lo screening dei singoli spazi dei parametri ha mostrato che l’esponente di potenza-legge di fMRI simulato dipendeva dall’equilibrio tra eccitazione a lungo raggio e inibizione locale: la distribuzione 2D della qualità di previsione delle serie temporali fMRI, la connettività funzionale e l’esponente di potenza-legge ha mostrato un caratteristico schema diagonale. Cioè, l’aumento dell’accoppiamento a lungo raggio richiedeva una maggiore inibizione del feedback locale per produrre le migliori previsioni di fMRI, FC ed esponenti della legge di potenza, il che ha dimostrato il ruolo cruciale dell’equilibrio E/I per l’emergere dell’invarianza di scala e delle correlazioni a lungo raggio(Figura 7-figure supplement 1 e Figura 7-figure supplement 2).
Discussione
In questo lavoro, descriviamo un modello di rete cerebrale biofisica che prevede una parte considerevole di serie temporali fMRI a riposo specifiche del soggetto sulla base di EEG misurati simultaneamente. È importante sottolineare come questo nuovo approccio modellistico possa essere utilizzato per dedurre i meccanismi neurofisiologici alla base dei segnali di neuroimaging. Invece di una semplice riproduzione delle osservazioni empiriche, il nostro obiettivo centrale è stato quello di fornire un quadro integrativo che unifica i dati empirici con la teoria del sistema nervoso al fine di ricavare i meccanismi delle funzioni cerebrali alla base delle osservazioni empiriche su molte scale. Chiaramente, la sequenza di analisi e di test di ipotesi implicite presentata in questo lavoro rappresenta una delle tante linee di indagine. Il punto più generale di questo rapporto è che il nostro modello ibrido può essere utilizzato sia per testare le ipotesi che per costruire ipotesi. In altre parole, molte delle domande (per le quali offriamo risposte) sono emerse solo durante l’applicazione del modello, il che ci ha permesso di perseguire una particolare narrazione nella comprensione della genesi di diversi fenomeni empirici. Un punto chiave di considerazione è che il modello del cervello è stato costruito a partire da reti di modelli di popolazione neurale generici, vincolati da dati empirici, ma non esplicitamente costruiti per affrontare specifici fenomeni riprodotti. Ciò è rispecchiato dall’emergere di processi a scale temporali notevolmente più veloci rispetto alle serie temporali fMRI specifiche del soggetto che erano l’obiettivo dell’adattamento del modello. È importante sottolineare che i meccanismi dedotti costituiscono ipotesi candidate che richiedono una falsificazione empirica. I meccanismi derivati dal modello fanno previsioni concrete sulle forme d’onda di diverse correnti di ingresso, sulla velocità di sparamento in uscita, sulle attività sinaptiche e sui segnali fMRI, che possono essere testati empiricamente. Attraverso la continua integrazione delle conoscenze biologiche, la falsificazione con i dati empirici e il successivo affinamento, i modelli di rete cerebrale ibrida sono destinati a rappresentare una teoria completa e sempre più accurata sulle funzioni cerebrali su larga scala. La costruzione di modelli di reti cerebrali ibride e i nostri principali risultati sono visualizzati nel Video 1.
I modelli ibridi attingono all’attività della sorgente EEG stimata empiricamente per limitare la dinamica della corrente di ingresso sinaptica. Questo approccio è motivato dalla necessità di un modello che non solo riproduca le caratteristiche statiche dell’attività cerebrale, come la connettività funzionale, ma che produca queste caratteristiche sulla base di dinamiche biologicamente plausibili delle serie temporali. Alla base dell’approccio c’è la considerazione che i target di BNM comunemente usati, come FC o le caratteristiche spettrali di potenza (ad esempio le oscillazioni lente di BOLD, EEG α-peak), possono in linea di principio essere generati da serie temporali che non sono, se non dalle caratteristiche montate, necessariamente biologicamente plausibili. Ad esempio, una vasta gamma di forme d’onda può produrre modelli di correlazione simili a FC senza necessariamente avere un supporto biologico. L’obiettivo non era quello di avere un convertitore astratto che semplicemente trasforma l’EEG in una modalità fMRI come le serie temporali. Piuttosto, l’attività della sorgente EEG serve come un’approssimazione delle correnti sinaptiche in corso specifiche del soggetto e l’adattamento dei parametri viene eseguito per sintonizzare il modello per spiegare in modo ottimale le serie temporali empiriche fMRI. A differenza di un semplice “convertitore”, il nostro modello biofisico è in grado di catturare altre caratteristiche dei dati funzionali del cervello non utilizzate per l’adattamento del modello. Mostriamo che in effetti lo spazio del parametro converge per diverse metriche dell’attività cerebrale verso un unico subspazio ottimale che indica la validità del nostro modello. Nel nostro approccio, entrambi i set di dati funzionali, EEG e fMRI, sono fusi nel quadro di un modello biofisicamente fondato e strutturalmente vincolato per approssimare in modo ottimale il comportamento sottostante (ma non osservabile) e i parametri del sistema reale. I modelli, per definizione, omettono le caratteristiche del sistema modellato per motivi di semplicità, generalità ed efficienza. L’aggiunta di gradi di libertà rende gli spazi dei parametri sempre più intrattabili e aumenta il rischio di un eccessivo adattamento. L’iniezione dell’attività della sorgente è un modo per sondare sistematicamente sistemi neurali sufficientemente astratti mantenendo un comportamento biologicamente realistico. In questo modo, l’approccio mira a bilanciare un livello di astrazione sufficiente a fornire intuizioni rilevanti, con un livello di dettaglio sufficiente a guidare il successivo studio empirico. L’obiettivo di questo approccio non è quello di raggiungere il più alto adattamento possibile tra le diverse modalità di imaging a costo della plausibilità biologica, che sarebbe il caso dei modelli statistici astratti che non si riferiscono ad entità biologiche e quindi precludono l’inferenza di conoscenze neurofisiologiche. In questo caso, la riproduzione imperfetta dell’attività neurale indica direttamente dei deficit nella nostra comprensione e nella concettualizzazione della struttura e della funzione cerebrale su larga scala, che per migliorare iterativamente è l’obiettivo di questo approccio. Notiamo che il nostro confronto delle qualità di previsione del modello ibrido e dei tre scenari di controllo non è un risultato nel senso di un confronto formale del modello, dove la bontà dell’adattamento è valutata alla luce della complessità del modello. Piuttosto, il confronto informale serve a valutare meglio la qualità di previsione del modello ibrido in relazione al modello originale e all’α-regressor. Anche se era a priori chiaramente improbabile che il modello basato sul rumore o l’iniezione di EEG permutati nel tempo si correlassero con le serie temporali empiriche, questi controlli servono ad escludere che le correlazioni del modello ibrido siano state ottenute da un meccanismo banale potenzialmente presente anche nei modelli di rumore. Inoltre, per verificare se è la specifica sequenza temporale dei punti temporali nell’attività iniettata che ha permesso la previsione della fMRI, abbiamo simulato la risposta del modello ibrido alle serie temporali di input permutati. Ancora più importante, queste correlazioni ci permettono di mostrare che, sebbene il rumore e l’input permutati non producano correlazioni di serie temporali degne di nota, come l’α-regressor, essi predicono comunque FC, mentre il modello ibrido predice sia le serie temporali che FC.Anche se l’α-regressor fa notevoli previsioni di serie temporali fMRI, esso produce basse correlazioni con FC e, cosa importante, non è in grado di prevedere i fenomeni neuronali elettrici che sono stati riprodotti con il modello ibrido in quanto non è basato su variabili di stato che corrispondono ad entità biologiche come il modello ibrido. Quindi, se durante il confronto formale del modello la complessità del modello è penalizzata senza tener conto dell’accuratezza del modello per prevedere diversi insiemi di dati che hanno origine da diverse modalità e che coinvolgono diversi tipi di metriche (come fa il modello ibrido), allora è probabile che l’α-regressor sia favorito, perché si basa su parametri liberi da zero mentre ottiene una previsione simile delle serie temporali, nonostante il fatto che ha chiaramente meno potere di spiegare contemporaneamente i diversi tipi di fenomeni neuronali spiegati dal modello ibrido. Al fine di valutare meglio la qualità relativa di questo tipo di modelli, stiamo lavorando su un quadro teorico che estende i quadri di identificazione dei sistemi bayesiani esistenti(Friston et al., 2003) per rendere conto della previsione simultanea delle dinamiche dei diversi fenomeni biologici, delle serie di dati e delle metriche, che va oltre l’ambito di questo studio e sarà oggetto di una pubblicazione supplementare.
L’idea dell’approccio ibrido è di testare come i modelli biofisici e strutturalmente vincolati rispondono a correnti di ingresso sinaptiche biologicamente plausibili, paragonabili a esperimenti in vivo o in vitro di iniezione di corrente elettrofisiologica. Tuttavia, va notato che il modello ibrido è chiaramente limitato dal fatto che non è un modello autonomo (autonomo) del cervello, ma dipende dall’attività esterna iniettata. Inoltre, l’approssimazione basata sull’EEG degli EPSC locali è limitata dalla risoluzione spaziale grossolana dell’EEG e dall’incapacità di distinguere gli EPSC locali da altre correnti che contribuiscono all’EEG, poiché tutte le correnti nel cervello si sovrappongono in un dato punto dello spazio per generare un potenziale in quel punto(Buzsáki et al., 2012). Questa limitazione diventerebbe evidente quando il modello ibrido è accoppiato con un modello in avanti per prevedere l’EEG sulla base dell’intera somma delle correnti in ingresso(Equazioni 1 e 2). Tuttavia, quando si prevede l’EEG sulla base di EPSC locali solo mediante l’applicazione del modello forward, si otterrebbe nuovamente l’EEG originale. In particolare, l’attività della sorgente EEG può essere vista solo come un’approssimazione degli EPSC e non è chiaro come l’EEG si riferisca esattamente agli EPSC, cioè a quale estensione questa approssimazione rifletta la realtà biologica. Anche se le considerazioni teoriche suggeriscono che i potenziali eccitatori postsinaptici dominano le ampiezze della densità di sorgente di corrente (CSD)(Mitzdorf, 1985), le osservazioni empiriche hanno ripetutamente mostrato eccezioni a questa proposizione. Ad esempio, i profili CSD di oscillazioni neuronali che sono stati trascinati in flussi di stimoli ritmici hanno mostrato un’alternanza temporale di stati dominati dalla depolarizzazione e dall’iperpolarizzazione dell’insieme netto, indicando il contributo degli IPSC ai profili CSD(Lakatos et al., 2008; Lakatos et al., 2013). Nonostante queste limitazioni sono stati riprodotti diversi fenomeni empirici e l’approccio dell’iniezione di input apre la strada a future ricerche per indagare i meccanismi neurali alla base di un’ampia gamma di fenomeni diversi. Per esempio, una caratteristica importante del ritmo α-ritmo è il suo caratteristico salto bistabile tra le modalità a bassa e ad alta potenza e una ‘dimora’ in ogni stato che segue un’esponenziale allungata (Freyer et al., 2009a). Questo comportamento è stato riprodotto molto da vicino da un modello corticotalamico multistabile che ha identificato il meccanismo sottostante come una commutazione multistabile tra un punto fisso e un attrattore del ciclo limite che è guidato dal rumore(Freyer et al., 2011). È importante notare che la riproduzione più vicina della commutazione EEG α nel modello di Freyer et al. (2011) è emersa solo quando il termine di rumore gaussiano non correlato (iniettato nei potenziali medi della membrana) è stato sostituito da un termine di rumore dipendente dallo stato (autoregressivo), che ha reso le fluttuazioni stocastiche iniettate effettivamente autocorrelate. Questo risultato è interessante nel contesto del presente studio in quanto le nostre simulazioni hanno identificato il passaggio tra le modalità di alta e bassa potenza del α-ritmo come un potenziale meccanismo generativo alla base delle oscillazioni dello stato a riposo della fMRI. A partire da questi risultati, i futuri studi BNM potrebbero indagare sistematicamente il ruolo dell’autocorrelazione rispetto agli input gaussiani e il loro impatto sulle dinamiche emergenti della fMRI (come le dinamiche FC), soprattutto perché input come l’attività della sorgente EEG utilizzata nel nostro modello ibrido catturano meglio la struttura di autocorrelazione delle correnti di sorgente biologica, che sono diverse dal rumore bianco(Haider et al., 2016; Okun et al., 2010).
In linea con i nostri risultati, gli studi a livello cellulare indicano che l’input ritmico GABAergico dalla rete interneuronale è associato al bilanciamento E/I(Dehghani et al., 2016) e alla cottura α (Jensene Mazaheri, 2010; Lorincz et al. , 2009; Osipova et al., 2008). Tuttavia, l’identificazione di un preciso meccanismo fisiologico che spiega come i ritmi α possano produrre un effetto inibitorio è rimasta elusiva (Jensene Mazaheri, 2010; Klimesch, 2012). Mazaheri e Jensen (2010) suggeriscono che l’inibizione α-correlata si verifica a causa di un’asimmetria di ampiezza osservata di oscillazioni in corso, anche chiamato baseline-shift. I nostri risultati suggeriscono, in accordo con il modello di Mazaheri e Jensen (2010), che un segnale di guida simmetrico oscillante nel range α porta a velocità di accensione asimmetrica e correnti sinaptiche, ma estendiamo questo schema con una spiegazione esplicita della generazione di impulsi inibitori da correnti di ingresso oscillanti. Inoltre, i nostri risultati con l’α-attività artificiale possono aiutare a gettare nuova luce sull’ipotesi del “gating by inhibition”, che presuppone che l’informazione sia indirizzata attraverso la rete cerebrale bloccando funzionalmente i percorsi rilevanti per il compito e che questa inibizione sia riflessa dall’α-attività (Jensen e Mazaheri, 2010). In accordo con questa ipotesi, abbiamo trovato che l’input a lungo raggio è diminuito durante gli stati di alta α-potenza e aumentato di nuovo quando α-potenza è diminuita, ma sono necessari ulteriori studi per esaminare l’effetto di α-potenza sulla comunicazione a lungo raggio e la sua interazione con altre bande di frequenza.
Non è chiaro in che misura i processi non neuronali influenzano il segnale fMRI, in quanto è stato dimostrato che diversi segnali fisiologici come la respirazione e la frequenza cardiaca sono correlati con le oscillazioni dello stato di riposo(Biswal et al., 1996; Power et al., 2017), che ha sollevato la preoccupazione che le oscillazioni RSN possano non essere correlate all’elaborazione delle informazioni neuronali, ma costituire piuttosto un epifenomeno(Birn et al., 2006; de Munck et al., 2008; Shmueli et al., 2007; Yuan et al., 2013). L’interpretazione e la gestione di queste modulazioni di segnale è quindi oggetto di un acceso dibattito e spesso sono considerate artefatte e rimosse dagli studi di fMRI(Birn et al., 2006; Chang e Glover, 2009). È importante notare, tuttavia, che le fluttuazioni di BOLD a bassa frequenza sono anche fortemente correlate con l’attività neurale elettrica, come è stato dimostrato da studi che hanno analizzato la fMRI insieme all’EEG(Goldman et al., 2002; Laufs et al., 2003; Moosmann et al., 2003), registrazioni intracorticali(He et al., 2008; Logothetis et al., 2001) o MEG(Brookes et al., 2011; de Pasquale et al., 2010). Allo stesso modo, forti correlazioni temporali e mappe di correlazione spazialmente simili di EEG α-potenza, respirazione e BOLD (Yuanet al., 2013), così come di EEG α-potenza, variazioni della frequenza cardiaca e BOLD (de Munck et al., 2008) suggeriscono che queste fluttuazioni fMRI non sono estranee all’attività neurale, ma possono essere di origine neurale.
I nostri risultati estendono la comprensione attuale mostrando un meccanismo esplicito per un’origine neurale delle oscillazioni fMRI RSN che spiega gran parte della loro varianza attraverso una catena di interazioni neurofisiologiche. Cioè, la nostra attività simulata non solo riproduce la correlazione negativa tra le fluttuazioni di α-potenza e il segnale di BOLD, ma rivela anche un meccanismo che trasforma le fluttuazioni di α-potenza in corso in oscillazioni fMRI. L’approccio ibrido costituisce quindi un approccio multimodale di fusione dei dati(Friston, 2009; Valdes-Sosa et al., 2009) che permette la caratterizzazione diretta delle correlazioni temporali precedentemente riportate tra i segnali BOLD ed EEG in termini di attività neurale sottostante e modelli espliciti in avanti. Oltre alle serie temporali fMRI, il modello ibrido riproduce anche la topologia spaziale delle reti fMRI, che non sono previste dal regressore di potenza α. Questi risultati si aggiungono così all’accumulo di prove che suggeriscono che le RSN hanno origine dall’attività neuronale(Brookes et al., 2011; de Pasquale et al., 2010; Goldman et al., 2002; He et al., 2008; Logothetis et al, 2001; Mantini et al., 2007; Moosmann et al., 2003) piuttosto che essere un fenomeno puramente emodinamico che è solo correlato, ma non causato da esso(Birn et al., 2006; de Munck et al., 2008; Shmueli et al., 2007). Le conclusioni di questi risultati hanno importanti implicazioni per i futuri studi di fMRI, in quanto implicano che le oscillazioni a bassa frequenza della fMRI possono essere attribuite a un processo neurale che ha un effetto considerevole, dipendente dallo stato, sull’elaborazione delle informazioni neurali, come indicato dalle grandi modulazioni della cottura neuronale e dell’attività sinaptica. I metodi per la correzione del rumore fisiologico potrebbero rimuovere la varianza dagli esperimenti fMRI che è correlata all’attività neuronale e possono quindi escludere informazioni rilevanti per l’interpretazione dei dati fMRI.
L’esplorazione dello spazio dei parametri mostra che l’accoppiamento strutturale è fondamentale per la previsione di fMRI, in quanto la qualità della previsione diminuisce per le forze di accoppiamento globale non ottimali o quando l’accoppiamento globale è disattivato del tutto(Figura 3-figure supplement 1, Figura 7-figure supplement 2). In questo studio non abbiamo affrontato l’effetto dei ritardi di accoppiamento, in quanto non essenziali per l’insorgere dei fenomeni descritti. La nostra applicazione iniziale del nuovo modello ibrido mirava a studiare l’effetto dell’iniezione di input minimizzando i gradi di libertà della simulazione e l’insieme dei parametri da variare. Ulteriori studi sono necessari per determinare l’effetto dei ritardi di accoppiamento, in quanto studi precedenti ne hanno dimostrato l’importante ruolo per le dinamiche emergenti su larga scala(Deco et al., 2011; Jirsa, 2008, 2009). Abbiamo osservato che la qualità di previsione dei tempi di attivazione della rete a riposo varia nel tempo ed è più alta nelle epoche di massima varianza della rispettiva modalità temporale. Durante queste, le finestre temporali delle reti a stato di riposo contribuiscono alla fMRI a tutto il cervello, cioè sono le più attive. Una possibile spiegazione può essere che durante gli stati di attività neurale asincrona (cioè quando la varianza dei modi temporali RSN è bassa) la conduzione del volume e la cancellazione delle onde elettromagnetiche diminuisce la capacità dei metodi di imaging della sorgente di ricostruire l’attività della sorgente.
E ‘importante notare che i processi osservati non può essere specifico per α-oscillazioni, ma può applicarsi anche ad altre frequenze o componenti del segnale non oscillatorio, per esempio, la scarica fase-locked dei neuroni si verifica su una gamma di bande di frequenza e non è limitato al α-ritmo (Buzsaki, 2006). Inoltre, l’α-ritmo, anche se prominente, non è certamente superiore ad altri ritmi rispetto al calcolo e alla cognizione neuronale (Fries, 2015). Infatti, può essere considerato come uno dei vari modi di funzionamento del cervello, anche durante il cosiddetto stato di riposo(Engel et al., 2013). Ulteriori studi empirici e teorici saranno necessari per affrontare queste limitazioni in modo più completo. Anche se la nostra analisi ruotava intorno alle α-oscillazioni, l’approccio di modellazione ibrida non si limita all’α-attività, in quanto l’attività della sorgente EEG iniettata non si limitava alla α-banda. L’approccio di modellazione ibrida in sé non pone alcun requisito sullo spettro di frequenza dell’attività della sorgente iniettata. È importante notare che la nostra attenzione sui ritmi α-ritmi non era “per costruzione”, ma, come sottolineato nell’introduzione, è emersa da una sequenza di analisi che abbiamo eseguito per capire come il modello ibrido ha generato la correlazione con le serie temporali empiriche fMRI. A questo proposito, è interessante notare che le correlazioni delle serie temporali ottenute dal regressore α e dal modello ibrido sono comparabili, il che indica che l’α-ritmo è stato il principale driver per la previsione delle serie temporali fMRI del modello ibrido.
Nonostante l’ubiquità delle dinamiche invarianti in scala, i modelli che generano distribuzioni di potenza-legge sono spesso piuttosto generici e distaccati dai dettagli dei sistemi modellati(Bak et al., 1987; Marković e Gros, 2014). Inoltre, non sono chiari i meccanismi precisi che portano all’emergere della scala dello spettro di potenza fMRI o la relazione tra l’interazione della rete cerebrale e la scala della potenza fMRI(He, 2011). I risultati della nostra simulazione indicano che il ridimensionamento dello spettro di potenza dello spettro fMRI è dovuto all’amplificazione osservata, dipendente dalla frequenza, dell’attività oscillatoria nelle reti che contengono un’eccitazione di feedback auto-rinforzante insieme a un lento decadimento dell’attività. Centrale nelle teorie sulla comparsa di criticità è la messa a punto di un parametro di controllo (ad esempio la forza di connessione) che porta il sistema ad un brusco cambiamento di uno o più parametri di ordine (ad esempio la velocità di scatto) quando il parametro di controllo viene spostato su un punto critico che segna il confine di una transizione di fase. È importante sottolineare che l’esistenza di leggi di potenza da sole non dimostra la criticità. Piuttosto, la criticità richiede l’esistenza di un parametro di controllo che può essere regolato per spostare il sistema attraverso una transizione di fase in un punto critico(Beggs e Timme, 2012). In vivo, i risultati in vitro e in silico mostrano che l’equilibrio dinamico tra eccitazione e inibizione si è rivelato essenziale per spostare il sistema verso o lontano dalla criticità, per esempio, alterando farmacologicamente l’equilibrio eccitazione-inibizione nei ratti anestetizzati(Osorio et al., 2010), nelle fette acute(Beggs e Plenz, 2003) o modificando i parametri che controllano l’eccitazione e l’inibizione globale nei modelli computazionali(Deco et al., 2014). Tuttavia, l’esatto ruolo giocato dall’equilibrio eccitazione-inibizione non è chiaro. In linea con questi risultati, abbiamo trovato che la scala della legge sulla potenza variava in funzione dei livelli relativi di eccitazione e inibizione globale, sottolineando ulteriormente la necessità di una relazione proporzionale tra questi parametri di controllo(Figura 7-figure supplement 2). A partire da questo, i risultati della nostra simulazione indicano che il bilanciamento E/I può causare una sintonizzazione delle forze relative degli ingressi locali e a lungo raggio alle popolazioni neurali che supporta l’interferenza costruttiva tra le diverse correnti di ingresso, che a sua volta amplifica le oscillazioni più lente più che le oscillazioni più rapide. Questi risultati affrontano una questione aperta sul fatto che le leggi di potenza nelle reti neurali derivino dal comportamento delle leggi di potenza a livello cellulare o da un processo globale a livello di rete(Beggs e Timme, 2012), dando una spiegazione per gli spettri di potenza fMRI senza scala come proprietà emergente dell’interazione a lungo raggio della rete cerebrale che non richiede processi decentralizzati su piccola scala come la costante sintonizzazione attiva dei parametri microscopici come proposto in alcune teorie di criticità auto-organizzata(Bak et al., 1987; Hesse e Gross, 2014). Inoltre, questi risultati affrontano esplicitamente l’effetto dell’attività di input, mentre gli studi in vitro e in silico si sono finora concentrati su sistemi senza input o con input notevolmente ridotti(Hesse e Gross, 2014). L’osservata co-emergenza di correlazioni spaziali a lungo raggio (cioè reti di connettività funzionale) e la scalatura della legge di potenza possono indicare una spiegazione unificante all’interno della teoria della criticità auto-organizzata, come precedentemente proposto da altri(Linkenkaer-Hansen et al., 2001). Si noti che abbiamo usato il modello ibrido non semplicemente per stabilire la prevalenza di dinamiche invarianti di scala, ma per usare la scala della legge di potenza in senso quantitativo per comprendere i meccanismi che portano a particolari esponenti della legge di potenza; per esempio, l’importanza delle connessioni estrinseche (tra nodi) nello spiegare le differenze tra la scala della legge di potenza a livello elettrofisiologico ed emodinamico. Questo è un punto importante perché un comportamento privo di scala di per sé sarebbe difficile da evitare in simulazioni di questo tipo.
Una vasta gamma di disturbi come l’autismo, la schizofrenia, le disabilità intellettuali, il morbo di Alzheimer, la sclerosi multipla o l’epilessia sono stati collegati a disturbi dell’equilibrio E/I (Marín, 2012) e a un’alterazione della connettività di rete strutturale e funzionale (Stam, 2014). L’approccio modellistico presentato può quindi giocare un ruolo chiave per identificare i precisi meccanismi alla base della fisiopatologia dei diversi disturbi e aiutare a sviluppare nuove terapie che ripristinino l’equilibrio E/I alterato o la connettività cerebrale, ad esempio, identificando i target per le terapie di stimolazione neurale o guidando una terapia personalizzata. La capacità del modello ibrido di dedurre precisi meccanismi neurofisiologici che danno origine a fenomeni empirici e di collegare i meccanismi coinvolti e i modelli di segnale attraverso diverse scale e modalità di neuroimaging lo rende uno strumento potenzialmente prezioso per la ricerca nelle neuroscienze.
Materiali e metodi
Modello computazionale
Il modello utilizzato in questo studio si basa sul modello di campo medio dinamico su larga scala utilizzato da Deco e colleghi(Deco et al., 2014; Wong e Wang, 2006). L’attività cerebrale è modellata come l’interazione in rete dei modelli di popolazione locale che rappresentano le aree corticali. Le regioni corticali sono modellate da modelli di massa neurale eccitatoria e inibitoria interconnessa. In contrasto con il modello originale, le connessioni eccitatorie sono state sostituite dall’attività della sorgente EEG iniettata. Il modello del campo medio dinamico approssima fedelmente l’evoluzione nel tempo delle attività sinaptiche medie e dei tassi di attivazione di una rete di neuroni a picco da un sistema di equazioni differenziali non lineari accoppiate per ogni nodo i:(1)Ii(E)=WEI0+G∑jCijSj(E)-JiSi(I)+wBG(E)IBG(2)Ii(I)=WII0-Si(I)+wBG(I)IBG(3)ri(E)=aEIi(E)-bE1-exp(-dE(aEIi(E)-bE))(4)ri(I)=aIIi(I)=aIIi(I)-bI1-exp(-dI(aIIi(I)-bI)))(5)dSi(E)(t)dt=-Si(E)τE+(1-Si(E))γEri(E)(6)dSi(I)(t)dt=-Si(I)τI+γIri(I)
Qui, ri(E,I) denota il tasso di cottura della popolazione della popolazione eccitatoria(E) e inibitoria(I) dell’area cerebrale i. Si(E,I) identifica la media delle variabili di gating sinaptico eccitatorio o inibitorio di ogni area cerebrale, mentre le loro correnti di ingresso sono date da Ii(E,I). A differenza del modello utilizzato da Deco et al. (2014) che ha un accoppiamento eccitatorio ricorrente e feedforward, noi approssimiamo le correnti eccitatorie postsinaptiche IBG utilizzando l’attività della sorgente EEG aggregata a livello regionale che viene aggiunta alla somma delle correnti in ingresso Ii(E,I). Questo approccio si basa su registrazioni intracorticali che suggeriscono che gli EPSC sono non casuali, ma fortemente correlati con i campi elettrici nelle loro vicinanze, mentre gli IPSC sono anticorrelati con gli EPSC(Haider et al., 2016). I parametri di peso ωBG(E,I) ridimensionare lo z-score normalizzato attività sorgente EEG normalizzata in modo indipendente per le popolazioni eccitatorie e inibitorie. G denota il fattore di scala della forza di accoppiamento a lungo raggio che ridimensiona la matrice di connettività strutturale Cij che denota la forza di interazione per ogni coppia di regioni i e j. Tutti e tre i parametri di scala sono stimati adattando i risultati della simulazione ai dati empirici della fMRI mediante una ricerca esaustiva. Inizialmente, lo spazio del parametro(lo spazio realen-dimensionale con n è il numero di parametri ottimizzati) era limitato in modo tale che la forza di inibizione era maggiore della forza di eccitazione, soddisfacendo un vincolo biologico. Inoltre, per ogni set di parametri testati (che contiene i tre parametri di scala sopra menzionati), i parametri regionali Ji che descrivono l’intensità dell’accoppiamento sinaptico locale inibitorio di retroazione per ogni area i (espresso in nA) sono dotati dell’algoritmo descritto di seguito in modo tale che il tasso di scatto medio di ogni popolazione eccitatoria nel modello fosse vicino a 3,06 Hz (cioè la funzione di costo per i parametri di sintonizzazione Ji si basava esclusivamente sui tassi di cottura medi e non sulla qualità delle previsioni). L’input esterno effettivo complessivo I0= 0,382 nA è scalato di WE e WI, per le piscine eccitatorie e inibitorie, rispettivamente. ri(E,I)indica le funzioni neuronali di ingresso-uscita (curve f-I) dei pool eccitatori e inibitori, rispettivamente. Tutti i parametri, ad eccezione di quelli che vengono sintonizzati durante la stima dei parametri, sono impostati come in Deco et al. (2014). Si prega di fare riferimento alla Tabella 1 per una specificazione delle variabili di stato e dei parametri. L’attività BOLD è stata simulata sulla base dell’attività sinaptica eccitatoria S(E) utilizzando il modello emodinamico Balloon-Windkessel(Friston et al., 2003), che è un modello dinamico che descrive la trasduzione dell’attività neuronale in cambiamenti di perfusione e l’accoppiamento della perfusione al segnale di BOLD. Il modello si basa sul presupposto che il segnale di BOLD è una funzione statica non lineare del contenuto totale normalizzato di deossiemoglobina voxel, del volume venoso normalizzato, della frazione di estrazione netta di ossigeno a riposo dal letto capillare e della frazione di volume del sangue a riposo. Si prega di fare riferimento a Deco et al. (2013) per l’insieme specifico delle equazioni del modello Ballon-Windkessel che abbiamo usato in questo studio.
| Quantità | Valore | Descrizione |
|---|---|---|
| Variabili di stato | ||
| ri(E,I) | Tasso di cottura della popolazione della popolazione eccitatoria(E) o inibitoria(I) nell’area cerebrale i | |
| Si(E,I) | Gating sinaptico medio | |
| Ii(E,I) | Somma di tutte le correnti in ingresso | |
| IBG | Correnti di ingresso derivate dall’EEG | |
| Parametri | ||
| w+ | 1.4 | Ricorrenza eccitante locale |
| Cij | Ottenuto dalla trattografia di diffusione | Matrice di connettività strutturale |
| γE, γI | 6.41 × 10−4, 1.0 × 10−3 | Parametri cinetici |
| aE, bE, dE, τE, WE | 310 (nC-1), 125 (Hz), 0,16 (s), 100 (ms), 1 | Variabili eccitanti di gating |
| aI, bI, dI, τI, WI | 615 (nC-1), 177 (Hz), 0,087 (s), 10 (ms), 0,7 | Variabili di gating inibitorie |
| JNMDA | 0,15 (nA) | Accoppiamento sinaptico eccitatorio |
| JI | Ottenuto da FIC euristico (nA) | Accoppiamento sinaptico inibitorio del feedback |
| I0 | 0,382 (nA) | ingresso esterno effettivo complessivo |
| G | Ottenuto dal montaggio del modello | Fattore di scala globale di accoppiamento |
| wBG(E), wBG(I) | Ottenuto dal montaggio del modello | Pesi per il dimensionamento delle correnti di ingresso derivate dall’EEG |
Ottimizzazione dei parametri
Per ogni modello di rete cerebrale, sono stati variati tre parametri per massimizzare l’adattamento tra fMRI empirica e simulata: il dimensionamento dell’accoppiamento eccitatorio della materia bianca e la forza degli input iniettati nelle popolazioni eccitatorie e inibitorie (si prega di fare riferimento alla Tabella 2 per una panoramica sui valori dei parametri ottenuti). A seguito di osservazioni in vivo(Xue et al., 2014), ci siamo assicurati che nelle popolazioni eccitatorie le ampiezze di EPSC siano più piccole delle ampiezze di IPSC limitando l’intervallo di valori per il rapporto ωBG(I) / ωBG(E) tra 5 e 200, che abbiamo trovato attraverso le simulazioni pilota iniziali. Si noti che il rapporto ωBG(I) / ωBG(E) non è identico al rapporto di ampiezza degli IPSCs vs. EPSCs, ma dipende anche dalle impostazioni specifiche di tutti gli altri vari parametri. Per esempio, un grande rapporto ωBG(I) / ωBG(E) può ancora portare ad un piccolo rapporto di ampiezza IPSCs vs. EPSCs se il parametro locale di inibizione del feedback Ji è piccolo. Oltre a queste simulazioni pilota iniziali per limitare il rapporto delle correnti postsinaptiche ad un range biologicamente plausibile, la combinazione specifica di tutti i vari parametri è stata trovata esclusivamente attraverso l’adattamento simulato a serie temporali empiriche fMRI sotto il vincolo della plausibilità del tiro. Cioè, oltre alla messa a punto di questi tre parametri globali utilizzando l’unico criterio di ottimizzazione di massimizzare l’adattamento tra le serie temporali fMRI simulate ed empiriche, abbiamo regolato le forze di accoppiamento inibitorie locali al fine di ottenere tassi di sparo biologicamente plausibili nelle popolazioni eccitatorie. Per questa seconda forma di regolazione, definita controllo dell’inibizione di feedback (FIC), i tassi medi di cottura della popolazione erano l’unico criterio di ottimizzazione, senza alcuna considerazione della qualità della previsione, che dipendeva solo dai tre parametri globali. FIC modula i punti di forza delle connessioni inibitorie che è necessario per compensare l’eccesso o la mancanza di eccitazione risultante dalla grande variabilità nella forza di accoppiamento di materia bianca ottenuta con la tractografia MRI, che è un prerequisito per ottenere intervalli plausibili di attività della popolazione che è rilevante per alcuni risultati(Figura 5 e Figura 6). La qualità della previsione è stata misurata come il coefficiente di correlazione medio tra tutte le serie temporali fMRI simulate ed empiriche di una parcella corticale completa su una lunghezza di 20,7 minuti (TR = 1,94 s, 640 punti di dati), quantificando così la capacità del modello di prevedere l’attività di 68 regioni corticali parcellate. Tenendo conto della natura su larga scala delle reti a stato di riposo fMRI, la dimensione della parcella scelta fornisce un parsimonioso compromesso tra la complessità del modello e il livello di spiegazione desiderato. Ciò che questa parcellizzazione può mancare in termini di dettaglio spaziale, guadagna nel fornire una copertura completa che può riprodurre in modo affidabile le onnipresenti caratteristiche su larga scala dei dati empirici, che presentiamo qui di seguito. Per escludere l’overfitting e la limitata generalizzabilità, sui risultati della simulazione del modello ibrido è stato eseguito uno schema di convalida incrociata di cinque volte. Pertanto, i dati sono stati suddivisi in modo casuale in due sottoinsiemi: 80% come sottoinsieme di addestramento e 20% come sottoinsieme di test. La qualità di previsione è stata stimata utilizzando il set di addestramento, prima che ai modelli addestrati venisse chiesto di prevedere il set di test. La qualità di previsione risultante è stata confrontata tra il training e il set di dati del test e tra il set di dati del test e i dati ottenuti dall’adattamento della serie temporale completa. Inoltre, nonostante l’ampia gamma di parametri possibili, la ricerca è convergente ad un massimo globale(Figura 3-figure supplement 1). Pertanto, abbiamo fatto in modo che, quando il modello è stato adattato ad un sottoinsieme di dati empirici, sia stato in grado di generalizzare a dati nuovi o non visti. A differenza degli approcci di selezione dei modelli, dove il potere predittivo dei diversi modelli e la loro complessità sono confrontati tra loro, noi qui usiamo solo un singolo tipo di modello.
| G | wBG(I) | wBG(I)/wBG(E) |
|---|---|---|
| 0.12 | 0.13 | 5 |
| 0.1 | 0.03 | 5 |
| 0.14 | 0.08 | 50 |
| 0.09 | 0.03 | 10 |
| 0.13 | 0.15 | 5 |
| 0.44 | 0.03 | 25 |
| 0.15 | 0.05 | 20 |
| 0.09 | 0.12 | 5 |
| 0.48 | 0.04 | 125 |
| 0.2 | 0.15 | 10 |
| 0.11 | 0.12 | 10 |
| 0.12 | 0.02 | 5 |
| 0.25 | 0.04 | 5 |
| 0.44 | 0.07 | 200 |
| 0.09 | 0.04 | 5 |
Controllo dell’inibizione del feedback
Le popolazioni eccitanti di nodi isolati del modello originale descritto in Deco et al. (2014) hanno una frequenza media di sparo di 3,06 Hz. Cioè, senza l’accoppiamento a lungo raggio G∑jCijSj(E) e senza attività iniettata wBG(E)IBG e wBG(I)IBG (cfr. equazioni 1 e 2), le popolazioni eccitatorie utilizzate hanno un tasso di cottura medio di 3,06 Hz. Questo valore è conforme all’attività corticale in vivo di Poisson-like misurata empiricamente di ~ 3 Hz (Softkye Koch, 1993; Wilson et al., 1994) ed è il risultato dell’approssimazione dinamica del campo medio del comportamento medio dell’insieme di un modello di neurone a picco su larga scala utilizzato in Deco et al. (2014). In contrasto con i nodi isolati, la velocità di accensione dei nodi accoppiati cambia nella dipendenza della matrice di connettività strutturale impiegata e dell’ingresso iniettato. Per compensare un eccesso o una mancanza di eccitazione risultante, è stato utilizzato un meccanismo di regolazione locale, chiamato feedback inhibition control (FIC). Questo approccio è stato precedentemente utilizzato con successo per migliorare significativamente la previsione del FC e per aumentare il repertorio dinamico dell’attività evocata e l’accuratezza della codifica degli stimoli esterni(Deco et al., 2014). Nonostante i vantaggi menzionati della sintonizzazione FIC, ha lo svantaggio di aumentare il numero di parametri aperti del modello. Per dimostrare che la qualità della previsione non è dovuta alla FIC, ma solo ai tre parametri globali e per escludere preoccupazioni circa l’eccessiva parametrizzazione o che la FIC può essere una condizione potenzialmente necessaria per l’emergere di una scala libera, abbiamo ideato un modello di controllo che non ha implementato la FIC, ma ha utilizzato un unico parametro globale per la forza di accoppiamento inibitoria. Invece di sintonizzare i 68 singoli pesi di accoppiamento locali individualmente, solo un singolo valore globale per tutti i pesi di accoppiamento inibitorio Ji era vario. Abbiamo confrontato l’effetto del FIC sulla qualità della previsione delle serie temporali e non abbiamo trovato alcuna differenza significativa nella qualità della previsione rispetto alle simulazioni che utilizzavano solo un unico valore per tutti i pesi di accoppiamento locali Ji per soggetto (test della somma dei gradi Wilcoxon a una coda, p=0,36, z= -0,37, delta di Cliffs d = -0,15). A differenza delle simulazioni che sono guidate dal rumore(Deco et al., 2014), i parametri FIC per l’ingresso iniettato devono essere stimati per l’intera serie temporale simulata, poiché la non stazionarietà delle serie temporali di stimolazione porta a notevoli fluttuazioni delle velocità di sparo. Pertanto, abbiamo sviluppato un algoritmo di ricerca locale per la stima veloce dei parametri FIC basato sull’algoritmo di Deco et al. (2014). Per esercitare la FIC, la forza sinaptica locale inibitoria locale viene regolata iterativamente fino a quando tutte le popolazioni eccitatorie non raggiungono un tasso di cottura vicino al tasso di cottura medio desiderato per l’intero ~20 min di attività. Durante ogni iterazione, l’algoritmo esegue una simulazione dell’intera serie temporale. Poi, calcola l’attività media di cottura per l’intera serie temporale per ogni popolazione eccitante e adatta Ji di conseguenza, cioè aumenta i valori locali Ji valori se il tasso di cottura medio su tutte le popolazioni eccitanti durante l’iterazione k-esimo r̂k è maggiore di 3,06 Hz e viceversa. Al fine di ridurre il numero di iterazioni il valore con cui Ji è modificato è, a differenza dell’algoritmo di Deco et al. (2014), adattato dinamicamente in funzione del rateo di cottura ottenuto durante l’iterazione corrente(7)Jik+1=Jik+(r^k-3.06)τkdove Jik denota il valore della forza di inibizione di feedback del nodo i e τk denota il fattore di sintonia adattiva durante l’iterazione k-th. Nella prima iterazione, tutti i Ji i valori sono inizializzati con uno e τk sono inizializzati con 0,005. Il fattore di sintonia adattativo viene modificato dinamicamente durante ogni iterazione in base al risultato dell’iterazione precedente:(8)τk+1=(∑i(Jik-1-Jk))/(r^k-1-r^k).
Nel caso in cui il risultato non sia migliorato durante l’iterazione corrente, cioè(9)|r^-3.06|≥|r^k-1-3.06|, il fattore di sintonia adattativo viene diminuito moltiplicandolo per 0.5 e l’algoritmo continua con la successiva iterazione. Dopo 12 iterazioni, tutte le Ji sono impostati sui valori che avevano durante l’iterazione k dove |r̂k – 3.06| era minimo.
Pre-elaborazione della risonanza magnetica
I connettimi strutturali e funzionali di 15 soggetti umani sani (fascia d’età: 18-31 anni, otto femmine) sono stati estratti da set di dati completi (RM ponderata per diffusione, RM ponderata T1, EEG-fMRI) utilizzando un’installazione locale di una pipeline per l’elaborazione automatica dei dati di RM funzionale e ponderata per diffusione (Schirneret al., 2015). Da un database locale di 49 soggetti (fascia di età 18-80 anni, 30 donne) acquisito per uno studio precedente (Schirneret al., 2015), abbiamo selezionato i 15 soggetti più giovani che soddisfacevano i più alti standard di qualità EEG dopo aver applicato le routine di correzione degli artefatti MR. La qualità EEG è stata valutata in base a standard definiti prima del progetto sperimentale e utilizzati abitualmente sul campo(Becker et al., 2011; Freyer et al., 2009b; Ritter et al., 2010; Ritter et al., 2007): presenza di picchi di frequenza > 20 Hz nelle densità spettrali di potenza, movimento eccessivo della testa e artefatti cardio-balistici. La ricerca è stata condotta in conformità al Codice Etico dell’Associazione Medica Mondiale (Dichiarazione di Helsinki). Il consenso informato scritto è stato fornito da tutti i soggetti con una comprensione dello studio prima della raccolta dei dati, ed è stato approvato dal comitato etico locale in conformità con le linee guida istituzionali del Charité Hospital di Berlino. Sono stati esclusi dall’esperimento i soggetti con una storia di malattie neurologiche, cognitive o psichiatriche autodenunciate. Strutturale (sequenza tridimensionale tridimensionale MP-RAGE ad alta risoluzione ponderata T1; TR = 1.900 ms, TE = 2,52 ms, TI = 900 ms, angolo di ribaltamento = 9°, campo visivo (FOV) = 256 mm x 256 mm x 192 mm, 256 × 256 × 192 Matrix, 1.0 mm di risoluzione isotropa voxel), ponderata per diffusione (sequenza ponderata T2; TR = 7500 ms, TE = 86 ms, FOV = 192 mm x 192 mm, 96 × 96 Matrix, 61 fette, 2.3 mm di risoluzione isotropa voxel, 64 direzioni di diffusione), e dati fMRI (sequenza di contrasto bidimensionale bidimensionale T2-ponderata di eco planare a gradiente di imaging planare del sangue in funzione del livello di ossigeno nel sangue; TR= 1.940 ms, TE = 30 ms, angolo di rotazione = 78°, FOV = 192 mm x 192 mm, risoluzione voxel 3 mm x 3 mm, spessore fetta 3 mm, matrice 64 × 64, 33 fette, 0.51 ms eco spaziatura, 668 TRs, 7 immagini iniziali sono state acquisite e scartate per permettere alla magnetizzazione di raggiungere l’equilibrio; occhio chiuso a riposo) sono state acquisite su uno scanner Siemens 3 Tesla Trio MRI a 12 canali presso il Berlin Center for Advanced Neuroimaging, Berlino, Germania. Le matrici di connettività strutturale estratte intendono dare una rappresentazione aggregata dei punti di forza dell’interazione tra le regioni come mediata dai tratti di fibra di materia bianca. Come nel modello originale di Deco et al. (2014), i ritardi di conduzione sono stati trascurati in questo studio in quanto non essenziali per le caratteristiche descritte. Matrici di forza Cij sono stati divisi per il rispettivo valore massimo di normalizzazione. In breve, la pipeline procede come segue: per ogni soggetto è stata utilizzata un’immagine tridimensionale ad alta risoluzione T1 ponderata per dividere la materia grigia corticale in 68 regioni secondo l’atlante Desikan-Killiany utilizzando la segmentazione anatomica automatica di FreeSurfer (Fischl, 2012) e registrata ai dati di diffusione. La parcellizzazione cerebrale basata sulla girandola è generata da un algoritmo di etichettatura probabilistica automatizzata che ha dimostrato di raggiungere un alto livello di accuratezza anatomica per l’identificazione delle regioni, pur tenendo conto di una vasta gamma di variabilità anatomica intersoggettiva(Desikan et al., 2006). L’atlante è stato utilizzato con successo in precedenti studi di modellazione e ha fornito relazioni struttura-funzione altamente significative(Honey et al., 2009; Ritter et al., 2013; Schirner et al., 2015). I dettagli sul pretrattamento ponderato per diffusione e sulla fMRI possono essere trovati in Schirner et al.(Schirner et al., 2015) In breve, la tractografia probabilistica della materia bianca e l’aggregazione delle tracce tra ogni coppia di regioni è stata eseguita come implementata nella pipeline automatica e la metrica di connessione distinta estratta. Questa metrica pesa il conteggio delle tracce grezze tra due regioni secondo il minimo delle aree di interfaccia materia grigia/materia bianca di entrambe le regioni utilizzate per collegare queste regioni in modo distinto ad altre metriche che utilizzano il conteggio delle tracce grezze non pesate, che è stato dimostrato essere influenzato da caratteristiche anatomiche specifiche del soggetto (vedi Schirner et al. (2015) per una discussione). Dopo la preelaborazione, la maschera di parcellazione corticale è stata registrata in base ai dati dello stato di riposo fMRI dei soggetti e sono stati estratti i segnali medi fMRI per ogni regione. Le prime cinque immagini di ogni scansione sono state scartate per consentire al segnale di risonanza magnetica di raggiungere lo stato di riposo. Per identificare l’attività RSN è stata eseguita una decomposizione spaziale ICA Group ICA per i dati fMRI di tutti i soggetti che utilizzavano FSL MELODIC(Beckmann e Smith, 2004) (MELODIC v4.0; FMRIB Oxford University, UK) con i seguenti parametri: filtro passa alto tagliato fuori: 100 s, correzione del movimento MCFLIRT, estrazione cerebrale BET, lisciatura spaziale 5 mm FWHM, normalizzazione a MNI152, concatenazione temporale, restrizione dimensionale a 30 componenti di uscita. I circuiti integrati che corrispondono alle RSN sono stati automaticamente identificati dalla correlazione spaziale con le 9 delle 10 coppie di reti ben assortite del database di attivazione 29.671 soggetti BrainMap come descritto in Smith et al. (2009) (esclusa la rete del cervelletto). Tutte le elaborazioni di immagini sono state eseguite nello spazio del soggetto nativo delle diverse modalità e l’atlante cerebrale è stato trasformato dallo spazio T1 del soggetto nei rispettivi spazi delle diverse modalità.
Pre-elaborazione EEG
I dettagli del pretrattamento EEG sono descritti nel materiale supplementare di Schirner et al.(Schirner et al., 2015). In primo luogo, per tener conto delle derive lente nei canali EEG e per migliorare la costruzione del modello durante la successiva correzione dell’artefatto di acquisizione di immagini MR (IAA), tutti i canali sono stati filtrati ad alta frequenza a 1,0 Hz (filtro FIR standard). La correzione IAA è stata eseguita utilizzando Analyser 2.0 (v2.0.2.5859, Brain Products, Gilching, Germania). L’inizio di ogni intervallo di scansione MRI è stato rilevato utilizzando un livello di trigger di gradiente di 300 µV/ms. I marker rilevati in modo errato, ad esempio a causa di eventi di shimming o di movimenti pesanti, sono stati respinti manualmente. Per assicurare il corretto rilevamento dei marcatori di inizio scansione risultanti, ogni intervallo inter-scan è stato controllato per la sua precisa lunghezza di 1940 ms (TR). Per ogni canale, è stato calcolato un modello dell’IAA utilizzando un approccio medio scorrevole (lunghezza della finestra: 11 intervalli) e successivamente sottratto da ogni intervallo di scansione. Per l’ulteriore elaborazione, i dati sono stati campionati a 200 Hz, importati in EEGLAB e filtrati a 60 Hz. Le tracce ECG sono state utilizzate per rilevare e marcare ogni istanza del complesso QRS al fine di identificare gli artefatti del balistocardiogramma (BCG). La posizione e la spaziatura ragionevole di questi marcatori ECG è stata controllata mediante ispezione visiva e corretta se necessario. Per correggere il BCG e gli artefatti indotti dall’attività muscolare, in particolare il movimento degli occhi, è stato calcolato un ICA temporale utilizzando l’algoritmo Infomax esteso come implementato in EEGLAB. Per identificare componenti indipendenti (ICs) che contengono artefatti BCG sono stati utilizzati come indicazione la trama topografica, le serie temporali di attivazione, gli spettri di potenza e il battito cardiaco innescato potenziali medi dei ICs risultanti. Sulla base delle caratteristiche stabilite, tutti i componenti che rappresentano il BCG sono stati identificati e respinti, cioè i componenti sono stati esclusi dalla retroproiezione. I restanti componenti artificiali, non-BCG, che rappresentano principalmente gli eventi di movimento, in particolare il movimento degli occhi, sono stati identificati in base alla loro localizzazione, attivazione, proprietà spettrali di potenza e ERP. Descrizioni dettagliate del preprocessing EEG e fMRI sono state pubblicate altrove(Becker et al., 2011; Freyer et al., 2009a; Ritter et al., 2010; Ritter et al., 2007).
Input del modello biologico
L’imaging della sorgente EEG è stato eseguito con il toolbox MATLAB Brainstorm, disponibile gratuitamente, utilizzando le impostazioni predefinite e la procedura standard per i dati EEG a riposo, come descritto nella documentazione del software(Tadel et al., 2011). I modelli spaziali di sorgente sono stati basati sulle singole triangolazioni della mesh corticale estratte da FreeSurfer dai dati della risonanza magnetica ponderata T1 di ciascun soggetto e decampionate da Brainstorm. Dagli stessi dati della risonanza magnetica, le triangolazioni della superficie della testa sono state calcolate da Brainstorm. Le posizioni standard dei condensatori EEG utilizzati (Easy-cap; 64 canali, compatibili con la risonanza magnetica) sono stati allineati dai punti di riferimento utilizzati in Brainstorm e proiettati sul punto più vicino della superficie della testa. I modelli in avanti sono basati sui modelli di testa del Boundary Element Method calcolati utilizzando il software open-source OpenMEEG e i modelli di generatori di dipoli perpendicolari 15002 situati ai vertici della triangolazione della superficie corticale. La soluzione inversa sLORETA è stata utilizzata per stimare la densità di corrente neuronale distribuita alla base dei dati misurati del sensore in quanto presenta un errore di localizzazione pari a zero(Pascual-Marqui, 2002). I dati EEG sono stati filtrati a 30 Hz e importati in Brainstorm. Lì, le epoche prima della prima e dopo l’ultima scansione fMRI sono state scartate e il segnale EEG è stato bloccato a tempo per i marcatori di inizio della scansione fMRI. Utilizzando le routine di brainstorm, i dati EEG sono stati proiettati sulla superficie corticale utilizzando il kernel di inversione ottenuto e mediati secondo la parcellazione Desikan-Killiany che è stata utilizzata anche per l’estrazione dei connettimi strutturali e funzionali e dei segnali fMRI mediati nella regione. Le risultanti 68 serie temporali di sorgenti a livello regionale sono state importate in MATLAB, z-score normalizzate e upsampled a 1000 Hz utilizzando l’interpolazione spline come implementato dalla funzione Octave interp1. Per consentire simulazioni efficienti, la frequenza di campionamento dell’attività iniettata era dieci volte inferiore alla frequenza di campionamento del modello. Pertanto, durante la simulazione sono stati iniettati valori identici durante ogni sequenza di 10 fasi di integrazione.
Simulazione ed analisi
Le simulazioni sono state eseguite con un’implementazione C altamente ottimizzata del modello precedentemente descritto sul supercomputer JURECA presso il Juelich Supercomputing Center. Il codice di simulazione e analisi e i dati utilizzati sono open source e disponibili presso i repository online(Schirner et al., 2017a, vedi “Disponibilità di dati e codice”). Una scansione esaustiva dello spazio dei parametri brute-force utilizzando 3888 combinazioni dei parametri G e ωBG(E,I) è stata eseguita per ogni soggetto. Ognuna di queste combinazioni è stata calcolata 12 volte per regolare in modo iterativo Ji valori. Come impostazione di controllo, sono state effettuate ulteriori simulazioni con permutazioni casuali delle serie temporali di ingresso. Pertanto, i singoli punti temporali di ogni serie temporale di attività della sorgente sono stati permutati in modo casuale (individualmente per ogni regione e soggetto) utilizzando la funzione Octave randperm() e iniettati nelle simulazioni utilizzando tutte le combinazioni di parametri precedentemente utilizzate. Come ulteriore situazione di controllo è stato simulato il modello di campo medio dinamico originale come descritto in Deco et al. (2014) per le 15 SC. Qui, i parametri G e JNMDA sono state variate e la sintonizzazione FIC è stata eseguita utilizzando lo stesso algoritmo utilizzato per il modello di iniezione dell’attività della sorgente. Il processo di simulazione e di ottimizzazione FIC è stato identico per tutti e tre i modelli. La lunghezza delle serie temporali simulate per ogni soggetto era di 21,6 min. Le simulazioni sono state eseguite ad una frequenza di campionamento del modello di 10.000 Hz. Le serie temporali BOLD sono state calcolate per ognidecimo passo temporale di attività di gating sinaptico eccitatorio utilizzando il modello Balloon-Windkessel(Friston et al., 2003). Poiché il modello Balloon-Windkessel agisce come un filtro passa-basso che attenua le frequenze superiori a ~ 0,15 Hz (Robinsonet al., 2006), un ulteriore filtro passa-basso non era necessario per il downsampling delle serie temporali fMRI simulate. Quindi, dalle serie temporali risultanti ogni 1940esimo passo è stato memorizzato per ottenere una frequenza di campionamento della fMRI simulata che fosse conforme alla fMRI TR empirica di 1,94 s. Le prime 11 scansioni (21,34 s) di attività sono state scartate per permettere l’attività del modello e il segnale fMRI simulato di stabilizzarsi. Per ogni soggetto e approccio di modellazione è stato utilizzato per tutte le analisi il risultato della simulazione che ha prodotto la più alta correlazione media tra tutte le 68 serie temporali delle regioni empiriche e simulate per tutti i parametri testati. Per garantire la specificità regionale dei risultati della simulazione, nel caso delle fMRI grezze sono state correlate solo le corrispondenti serie temporali simulate e le serie temporali delle regioni empiriche, rispettivamente, per le reti a stato di riposo sono state utilizzate per la stima della qualità della previsione solo regioni simulate che si sovrappongono al modello di attivazione spaziale della rispettiva rete. In particolare, per l’analisi delle RSN, sono state confrontate solo quelle regioni con le modalità temporali delle RSN che avevano una sovrapposizione spaziale di almeno il 40% di tutti i voxel appartenenti alla rispettiva regione. Per valutare la qualità di previsione variabile nel tempo, è stata eseguita un’analisi di correlazione in cui una finestra con una lunghezza di 100 scansioni (194 s) è stata fatta scorrere sulle 68 coppie di serie temporali empiriche e simulate e la correlazione media su tutte le 68 regioni è stata calcolata per ogni finestra. Per la stima della correlazione dei segnali, è stato utilizzato il calcolo delle voci delle matrici FC e come misura della somiglianza delle matrici FC di Pearson, il coefficiente di correlazione lineare. Le matrici FC sono state confrontate impilando tutti gli elementi al di sotto della diagonale principale in vettori e calcolando il coefficiente di correlazione di questi vettori. La qualità di previsione FC a breve termine è stata stimata calcolando la correlazione media ottenuta per tutte le correlazioni a finestra di un’analisi a finestra scorrevole di serie temporali empiriche e simulate (dimensione della finestra: 100 scansioni = 194 s).
Per garantire l’assenza di scala dei segnali empirici e simulati, le serie temporali delle regioni sono state testate utilizzando rigorosi criteri di selezione del modello; in media il 79% di tutte le 1020 serie temporali a livello di regione (15 soggetti x 68 regioni) per i sette tipi di segnale analizzati (fMRI empirica, fMRI simulata, fMRI simulata senza accoppiamento globale, fMRI simulata senza FIC, fMRI simulata senza FIC e senza accoppiamento globale, α-potenza, α-regressor) testato come privo di scala; per ogni tipo di segnale ogni soggetto aveva almeno cinque regioni da testare come privo di scala. I PSD sono stati calcolati usando il metodo di Welch come implementato in Octave, normalizzati per la loro potenza totale e mediati. Gli spettri di potenza media risultanti erano dotati di una funzione di legge sulla potenza f(x)=axβ utilizzando la stima dei minimi quadrati nella gamma di frequenza 0,01 Hz e 0,17 Hz che è identica alla gamma per la quale è stata eseguita la prova di invarianza di scala. Le frequenze sotto riportate sono state escluse al fine di ridurre l’impatto dei confound del segnale a bassa frequenza e della deriva dello scanner, le frequenze al di sopra di tale limite sono state escluse per evitare artefatti di aliasing in intervalli di frequenza più elevati (TR = 1,94 s, quindi la frequenza di Nyquist si aggira intorno a 0,25 Hz). Al fine di confrontare l’invarianza di scala dei nostri dati empirici fMRI con i risultati delle precedenti pubblicazioni(He, 2011), abbiamo anche calcolato gli spettri di potenza in un intervallo che comprendeva solo frequenze < 0,1 Hz.
Per determinare adeguatamente l’esistenza dell’invarianza di scala abbiamo applicato una rigorosa selezione del modello ad ogni serie temporale per identificare la scala della legge di potenza ed abbiamo escluso tutte le serie temporali dalle analisi che sono state descritte meglio da un modello diverso da quello della legge di potenza. Tuttavia, abbiamo confrontato i risultati ottenuti da questo rigoroso regime con quelli ottenuti quando tutte le serie temporali sono state incluse e li abbiamo trovati qualitativamente identici. Per verificare l’esistenza dell’invarianza di scala abbiamo utilizzato un metodo che combina una versione modificata della ben consolidata analisi di fluttuazione detentrice (DFA) con il confronto del modello bayesiano(Ton e Daffertshofer, 2016). La DFA è, a differenza delle analisi PSD, robusta sia per i dati stazionari che per quelli non stazionari in presenza di tendenze confuse (debolmente non lineari). È importante notare che un semplice adattamento lineare della curva di fluttuazione detentrice senza un adeguato confronto della bontà di adattamento ottenuta con quella di altri modelli ignorerebbe completamente le rappresentazioni alternative dei dati diverse da una legge di potenza. Per la quantificazione della bontà dell’adattamento con la semplice regressione il suo corrispondente coefficiente di determinazione, R2è inadatto in quanto misura solo la forza di un rapporto lineare ed è inadeguato per la regressione non lineare(Ton e Daffertshofer, 2016). È importante notare che con questo metodo la valutazione della scala di potenza-legge si basa sulla stima della massima probabilità, che supera i limiti di una stima minima di minimi quadrati ottenuta dalla regressione lineare nell’approccio DFA convenzionale. I dettagli del metodo utilizzato sono descritti altrove(Ton e Daffertshofer, 2016). Per i diversi segnali la maggior parte delle serie temporali è stata testata come priva di scala: 83% per fMRI empirica, 69% per fMRI simulata, 71% per fMRI simulata con FIC disattivato, 83% per fMRI simulata con accoppiamento globale disattivato, 86% per fMRI simulata con accoppiamento globale disattivato e FIC, 90% per α-potenza e 70% per il regressore α.
Per calcolare la grande media delle forme d’onda, le variabili di stato sono state calcolate in media su tutti i 15 soggetti e 68 regioni(N= serie temporali di 1020 regioni) bloccate al passaggio a zero dell’ampiezza α, che è stato ottenuto filtrando le serie temporali di attività della sorgente tra 8 e 12 Hz; per ottenere forme d’onda medie nette, sono state utilizzate tutte le epoche di α-ciclo con una lunghezza d’onda compresa tra 95 e 105 ms (N = 4.137.994 α-ciclo). Per il calcolo dei corsi temporali di α-potenza in corso, sono state calcolate serie temporali di potenza istantanea prendendo il valore assoluto del segnale analitico (ottenuto dalla trasformata di Hilbert) dell’attività della sorgente filtrata passa-banda nella gamma di frequenza 8-10 Hz; il primo e l’ultimo ~50 s sono stati scartati per il controllo degli effetti di bordo. Per calcolare l’α-regressor, le serie temporali di potenza sono state convolte con la funzione di risposta emodinamica canonica, sottocampionate alla frequenza di campionamento fMRI e spostate rispetto alle serie temporali fMRI per tener conto del ritardo della risposta emodinamica. Per il confronto con i risultati della simulazione è stata utilizzata la più alta correlazione media negativa su tutte le 68 coppie di regioni ottenute entro un intervallo di spostamento di ±3 scansioni.
Analisi statistiche
Tutte le analisi statistiche sono state effettuate utilizzando MATLAB (The MathWorks, Inc., Natick, Massachusetts, Stati Uniti). I dati sono rappresentati come diagrammi a scatola e baffi. Poiché la normalità non è stata raggiunta per la maggior parte dei set di dati (valutati dal test di Lilliefors a livello di significatività di 0,05), le differenze tra i gruppi sono state confrontate con test statistici non parametrici, utilizzando o il test di somma del rango Wilcoxon a due code o, in caso di previsione direzionale, il test di somma del rango Wilcoxon a una coda; un valore p<0,05 è stato considerato significativo.
Disponibilità di dati e codici
I modelli di rete cerebrale sono implementati nella piattaforma neuroinformatica open source The Virtual Brain(Ritter et al., 2013; Sanz-Leon et al., 2015, Sanz Leon et al., 2013) che può essere scaricata da thevirtualbrain.org. Il codice e i dati che supportano i risultati di questo studio possono essere ottenuti da https://github.com/BrainModes/The-Hybrid-Virtual-Brain(Schirner et al., 2017b; copia archiviata su https://github.com/elifesciences-publications/The-Hybrid-Virtual-Brain) e https://osf.io/mndt8/(Schirner et al., 2017a).
References
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD. Tracking whole-brain connectivity dynamics in the resting state. Cerebral Cortex. 2014; 24:663-676. DOI | PubMed
- Atallah BV, Scanziani M. Instantaneous modulation of gamma oscillation frequency by balancing excitation with inhibition. Neuron. 2009; 62:566-577. DOI | PubMed
- Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters. 1987; 59:381-384. DOI | PubMed
- Bak P. How nature works: the science of self-organized criticality. Springer Science & Business Media; 2013.
- Becker R, Reinacher M, Freyer F, Villringer A, Ritter P. How ongoing neuronal oscillations account for evoked fMRI variability. Journal of Neuroscience. 2011; 31:11016-11027. DOI | PubMed
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2004; 23:137-152. DOI | PubMed
- Beggs JM, Plenz D. Neuronal avalanches in neocortical circuits. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2003; 23:11167-11177. PubMed
- Beggs JM, Timme N. Being critical of criticality in the brain. Frontiers in Physiology. 2012; 3DOI | PubMed
- Berger H. Über das elektrenkephalogramm des menschen. European Archives of Psychiatry and Clinical Neuroscience. 1929; 87:527-570. DOI
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. NeuroImage. 2006; 31:1536-1548. DOI | PubMed
- Biswal B, DeYoe EA, Hyde JS. Reduction of physiological fluctuations in fMRI using digital filters. Magnetic Resonance in Medicine. 1996; 35:107-113. DOI | PubMed
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine. 1995; 34:537-541. DOI | PubMed
- Breakspear M. Dynamic models of large-scale brain activity. Nature Neuroscience. 2017; 20:340-352. DOI | PubMed
- Brookes MJ, Woolrich M, Luckhoo H, Price D, Hale JR, Stephenson MC, Barnes GR, Smith SM, Morris PG. Investigating the electrophysiological basis of resting state networks using magnetoencephalography. PNAS. 2011; 108:16783-16788. DOI | PubMed
- Busch NA, Dubois J, VanRullen R. The phase of ongoing EEG oscillations predicts visual perception. Journal of Neuroscience. 2009; 29:7869-7876. DOI | PubMed
- Buzsaki G. Rhythms of the Brain. Oxford University Press: New York, United States; 2006. DOI
- Buzsáki G, Anastassiou CA, Koch C. The origin of extracellular fields and currents–EEG, ECoG, LFP and spikes. Nature Reviews Neuroscience. 2012; 13:407-420. DOI | PubMed
- Chang C, Glover GH. Relationship between respiration, end-tidal CO2, and BOLD signals in resting-state fMRI. NeuroImage. 2009; 47:1381-1393. DOI | PubMed
- de Munck JC, Gonçalves SI, Faes TJ, Kuijer JP, Pouwels PJ, Heethaar RM, Lopes da Silva FH, da Silva FL. A study of the brain’s resting state based on alpha band power, heart rate and fMRI. NeuroImage. 2008; 42:112-121. DOI | PubMed
- de Pasquale F, Della Penna S, Snyder AZ, Lewis C, Mantini D, Marzetti L, Belardinelli P, Ciancetta L, Pizzella V, Romani GL, Corbetta M. Temporal dynamics of spontaneous MEG activity in brain networks. PNAS. 2010; 107:6040-6045. DOI | PubMed
- Deco G, Jirsa VK, McIntosh AR. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience. 2011; 12:43-56. DOI | PubMed
- Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston K. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Computational Biology. 2008; 4DOI | PubMed
- Deco G, Ponce-Alvarez A, Hagmann P, Romani GL, Mantini D, Corbetta M. How local excitation-inhibition ratio impacts the whole brain dynamics. Journal of Neuroscience. 2014; 34:7886-7898. DOI | PubMed
- Deco G, Ponce-Alvarez A, Mantini D, Romani GL, Hagmann P, Corbetta M. Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. Journal of Neuroscience. 2013; 33:11239-11252. DOI | PubMed
- Dehghani N, Peyrache A, Telenczuk B, Le Van Quyen M, Halgren E, Cash SS, Hatsopoulos NG, Destexhe A. Dynamic balance of excitation and inhibition in human and monkey neocortex. Scientific Reports. 2016; 6DOI | PubMed
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006; 31:968-980. DOI | PubMed
- Engel AK, Gerloff C, Hilgetag CC, Nolte G. Intrinsic coupling modes: multiscale interactions in ongoing brain activity. Neuron. 2013; 80:867-886. DOI | PubMed
- Feige B, Scheffler K, Esposito F, Di Salle F, Hennig J, Seifritz E. Cortical and subcortical correlates of electroencephalographic alpha rhythm modulation. Journal of Neurophysiology. 2005; 93:2864-2872. DOI | PubMed
- Fischl B. Freesurfer. NeuroImage. 2012; 62:774-781. DOI | PubMed
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature Reviews Neuroscience. 2007; 8:700-711. DOI | PubMed
- Freyer F, Aquino K, Robinson PA, Ritter P, Breakspear M. Bistability and non-Gaussian fluctuations in spontaneous cortical activity. Journal of Neuroscience. 2009a; 29:8512-8524. DOI | PubMed
- Freyer F, Becker R, Anami K, Curio G, Villringer A, Ritter P. Ultrahigh-frequency EEG during fMRI: pushing the limits of imaging-artifact correction. NeuroImage. 2009b; 48:94-108. DOI | PubMed
- Freyer F, Roberts JA, Becker R, Robinson PA, Ritter P, Breakspear M. Biophysical mechanisms of multistability in resting-state cortical rhythms. Journal of Neuroscience. 2011; 31:6353-6361. DOI | PubMed
- Fries P. Rhythms for cognition: communication through coherence. Neuron. 2015; 88:220-235. DOI | PubMed
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003; 19:1273-1302. DOI | PubMed
- Friston KJ. Modalities, modes, and models in functional neuroimaging. Science. 2009; 326:399-403. DOI | PubMed
- Goldman RI, Stern JM, Engel J, Cohen MS. Simultaneous EEG and fMRI of the alpha rhythm. NeuroReport. 2002; 13:2492. DOI | PubMed
- Haegens S, Nácher V, Luna R, Romo R, Jensen O. α-Oscillations in the monkey sensorimotor network influence discrimination performance by rhythmical inhibition of neuronal spiking. PNAS. 2011; 108:19377-19382. DOI | PubMed
- Haider B, Schulz DP, Häusser M, Carandini M. Millisecond coupling of local field potentials to synaptic currents in the awake visual cortex. Neuron. 2016; 90:35-42. DOI | PubMed
- He BJ, Snyder AZ, Zempel JM, Smyth MD, Raichle ME. Electrophysiological correlates of the brain’s intrinsic large-scale functional architecture. PNAS. 2008; 105:16039-16044. DOI | PubMed
- He BJ. Scale-free properties of the functional magnetic resonance imaging signal during rest and task. Journal of Neuroscience. 2011; 31:13786-13795. DOI | PubMed
- Hesse J, Gross T. Self-organized criticality as a fundamental property of neural systems. Frontiers in Systems Neuroscience. 2014; 8DOI | PubMed
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. PNAS. 2009; 106:2035-2040. DOI | PubMed
- Isaacson JS, Scanziani M. How inhibition shapes cortical activity. Neuron. 2011; 72:231-243. DOI | PubMed
- Jensen O, Mazaheri A. Shaping functional architecture by oscillatory alpha activity: gating by inhibition. Frontiers in Human Neuroscience. 2010; 4DOI | PubMed
- Jirsa VK. Dispersion and time delay effects in synchronized spike-burst networks. Cognitive Neurodynamics. 2008; 2:29-38. DOI | PubMed
- Jirsa VK. Neural field dynamics with local and global connectivity and time delay. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2009; 367:1131-1143. DOI | PubMed
- Kirschstein T, Köhling R. What is the source of the EEG?. Clinical EEG and Neuroscience. 2009; 40:146-149. DOI | PubMed
- Klimesch W, Sauseng P, Hanslmayr S. EEG alpha oscillations: the inhibition-timing hypothesis. Brain Research Reviews. 2007; 53:63-88. DOI | PubMed
- Klimesch W. EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Research Reviews. 1999; 29:169-195. DOI | PubMed
- Klimesch W. α-band oscillations, attention, and controlled access to stored information. Trends in Cognitive Sciences. 2012; 16:606-617. DOI | PubMed
- Krause D, Thörnig P. JURECA: general-purpose supercomputer at jülich supercomputing centre. Journal of Large-Scale Research Facilities JLSRF. 2016; 2DOI
- Lakatos P, Karmos G, Mehta AD, Ulbert I, Schroeder CE. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science. 2008; 320:110-113. DOI | PubMed
- Lakatos P, Musacchia G, O’Connel MN, Falchier AY, Javitt DC, Schroeder CE. The spectrotemporal filter mechanism of auditory selective attention. Neuron. 2013; 77:750-761. DOI | PubMed
- Laufs H, Kleinschmidt A, Beyerle A, Eger E, Salek-Haddadi A, Preibisch C, Krakow K. EEG-correlated fMRI of human alpha activity. NeuroImage. 2003; 19:1463-1476. DOI | PubMed
- Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. Long-range temporal correlations and scaling behavior in human brain oscillations. Journal of Neuroscience. 2001; 21:1370-1377. PubMed
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001; 412:150-157. DOI | PubMed
- Lorincz ML, Kékesi KA, Juhász G, Crunelli V, Hughes SW. Temporal framing of thalamic relay-mode firing by phasic inhibition during the alpha rhythm. Neuron. 2009; 63:683-696. DOI | PubMed
- Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M. Electrophysiological signatures of resting state networks in the human brain. PNAS. 2007; 104:13170-13175. DOI | PubMed
- Marín O. Interneuron dysfunction in psychiatric disorders. Nature Reviews Neuroscience. 2012; 13:107-120. DOI | PubMed
- Marković D, Gros C. Power laws and self-organized criticality in theory and nature. Physics Reports. 2014; 536:41-74. DOI
- Mathewson KE, Gratton G, Fabiani M, Beck DM, Ro T. To see or not to see: prestimulus alpha phase predicts visual awareness. Journal of Neuroscience. 2009; 29:2725-2732. DOI | PubMed
- Mazaheri A, Jensen O. Rhythmic pulsing: linking ongoing brain activity with evoked responses. Frontiers in Human Neuroscience. 2010; 4DOI | PubMed
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiological Reviews. 1985; 65:37-100. DOI | PubMed
- Moosmann M, Ritter P, Krastel I, Brink A, Thees S, Blankenburg F, Taskin B, Obrig H, Villringer A. Correlates of alpha rhythm in functional magnetic resonance imaging and near infrared spectroscopy. NeuroImage. 2003; 20:145-158. DOI | PubMed
- Nunez PL, Srinivasan R. Electric Fields of the Brain: The Neurophysics of EEG. Oxford University Press; 2006. DOI
- Okun M, Lampl I. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nature Neuroscience. 2008; 11:535-537. DOI | PubMed
- Okun M, Naim A, Lampl I. The subthreshold relation between cortical local field potential and neuronal firing unveiled by intracellular recordings in awake rats. Journal of Neuroscience. 2010; 30:4440-4448. DOI | PubMed
- Osipova D, Hermes D, Jensen O. Gamma power is phase-locked to posterior alpha activity. PLoS One. 2008; 3DOI | PubMed
- Osorio I, Frei MG, Sornette D, Milton J, Lai Y-C. Epileptic seizures: quakes of the brain?. Physical Review E. 2010; 82DOI
- Pascual-Marqui RD. Standardized low-resolution brain electromagnetic tomography (sLORETA): technical details. Methods and Findings in Experimental and Clinical Pharmacology. 2002; 24:5-12. PubMed
- Power JD, Plitt M, Laumann TO, Martin A. Sources and implications of whole-brain fMRI signals in humans. NeuroImage. 2017; 146:609-625. DOI | PubMed
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. PNAS. 2001; 98:676-682. DOI | PubMed
- Ritter P, Becker R, Freyer F, Villringer A. EEG Quality: The Image Acquisition Artefact EEG-fMRI. Springer; 2010.
- Ritter P, Becker R, Graefe C, Villringer A. Evaluating gradient artifact correction of EEG data acquired simultaneously with fMRI. Magnetic Resonance Imaging. 2007; 25:923-932. DOI | PubMed
- Ritter P, Moosmann M, Villringer A. Rolandic alpha and beta EEG rhythms’ strengths are inversely related to fMRI-BOLD signal in primary somatosensory and motor cortex. Human Brain Mapping. 2009; 30:1168-1187. DOI | PubMed
- Ritter P, Schirner M, McIntosh AR, Jirsa VK. The virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connectivity. 2013; 3:121-145. DOI | PubMed
- Robinson PA, Drysdale PM, Van der Merwe H, Kyriakou E, Rigozzi MK, Germanoska B, Rennie CJ. BOLD responses to stimuli: dependence on frequency, stimulus form, amplitude, and repetition rate. NeuroImage. 2006; 31:585-599. DOI | PubMed
- Sanz Leon P, Knock SA, Woodman MM, Domide L, Mersmann J, McIntosh AR, Jirsa V. The Virtual Brain: a simulator of primate brain network dynamics. Frontiers in Neuroinformatics. 2013; 7DOI | PubMed
- Sanz-Leon P, Knock SA, Spiegler A, Jirsa VK. Mathematical framework for large-scale brain network modeling in The Virtual Brain. NeuroImage. 2015; 111:385-430. DOI | PubMed
- Schirner M, McIntosh AR, Jirsa V, Deco G, Ritter P. Hybrid brain model data. Open Science Framework. 2017a. DOI
- Schirner M, McIntosh AR, Jirsa V, Deco G, Ritter P. The-Hybrid-Virtual-Brain. Github. 2017b. Publisher Full Text
- Schirner M, Rothmeier S, Jirsa VK, McIntosh AR, Ritter P. An automated pipeline for constructing personalized virtual brains from multimodal neuroimaging data. NeuroImage. 2015; 117:343-357. DOI | PubMed
- Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. NeuroImage. 2007; 38:306-320. DOI | PubMed
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. PNAS. 2009; 106:13040-13045. DOI | PubMed
- Softky WR, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. Journal of Neuroscience. 1993; 13:334-350. PubMed
- Stam CJ. Modern network science of neurological disorders. Nature Reviews Neuroscience. 2014; 15:683-695. DOI | PubMed
- Tadel F, Baillet S, Mosher JC, Pantazis D, Leahy RM. Brainstorm: a user-friendly application for MEG/EEG analysis. Computational Intelligence and Neuroscience. 2011; 2011:1-13. DOI | PubMed
- Ton R, Daffertshofer A. Model selection for identifying power-law scaling. NeuroImage. 2016; 136:215-226. DOI | PubMed
- Valdes-Sosa PA, Sanchez-Bornot JM, Sotero RC, Iturria-Medina Y, Aleman-Gomez Y, Bosch-Bayard J, Carbonell F, Ozaki T. Model driven EEG/fMRI fusion of brain oscillations. Human Brain Mapping. 2009; 30:2701-2721. DOI | PubMed
- Wilson FA, O’Scalaidhe SP, Goldman-Rakic PS. Functional synergism between putative gamma-aminobutyrate-containing neurons and pyramidal neurons in prefrontal cortex. PNAS. 1994; 91:4009-4013. DOI | PubMed
- Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. Journal of Neuroscience. 2006; 26:1314-1328. DOI | PubMed
- Xue M, Atallah BV, Scanziani M. Equalizing excitation-inhibition ratios across visual cortical neurons. Nature. 2014; 511:596-600. DOI | PubMed
- Yuan H, Zotev V, Phillips R, Bodurka J. Correlated slow fluctuations in respiration, EEG, and BOLD fMRI. NeuroImage. 2013; 79:81-93. DOI | PubMed
Fonte
Schirner M, McIntosh AR, Jirsa V, Deco G, Ritter P, et al. () Inferring multi-scale neural mechanisms with brain network modelling. eLife 7e28927. https://doi.org/10.7554/eLife.28927





