Abstract
Introduzione
La percezione viene sempre più spesso percepita attraverso l’integrazione corticale di segnali “dal basso verso l’alto” o sensoriali e di informazioni “dall’alto verso il basso”. Le esperienze precedenti, le aspettative e la conoscenza del mondo permettono la formazione di priori o di ipotesi sullo stato del mondo esterno (cioè le cause dell’input sensoriale) che aiutano, attraverso segnali top-down, a risolvere l’ambiguità nei segnali sensoriali bottom-up. Tali rappresentazioni neuronali, o ‘state-units’, possono poi essere ottimizzate alla luce di nuovi input sensoriali. I primi modelli di elaborazione neurale che implementavano tale quadro di codifica predittiva incorporavano esplicitamente la conoscenza preliminare delle regolarità statistiche nell’ambiente(Srinivasan et al., 1982). I conti contemporanei trattano queste idee in termini di inferenza bayesiana e di minimizzazione degli errori di previsione(Rao e Ballard, 1999; Friston, 2005; Friston e Stephan, 2007; Hohwy, 2013; Clark, 2013).
Questa percezione è essenzialmente un processo inferenziale ed è supportata da molti risultati comportamentali che dimostrano il ruolo significativo delle informazioni contestuali(Geisler e Kersten, 2002; Kersten et al., 2004; Kok e Lange, 2015; Weiss et al., 2002) e dei segnali dall’alto verso il basso(Kok et al., 2012b, Pascual-Leone e Walsh, 2001; Ro et al., 2003; Vetter et al., 2014) nella percezione. Diversi studi suggeriscono inoltre diverse misure neurali di segnali di feedforward e feedback(Hupe et al., 1998) principalmente in termini di bande di frequenza oscillatorie caratteristiche(Bastos et al., 2015; Buschman e Miller, 2007; Fontolan et al., 2014; Mayer et al., 2016; Michalareas et al., 2016; Sherman et al., 2016; van Kerkoerle et al., 2014).
Tuttavia, lo studio delle basi neurali della percezione richiede non solo la distinzione tra segnali dall’alto verso il basso e dal basso verso l’alto, ma anche l’esame dell’effettiva integrazione tra tali segnali. Ciò è particolarmente importante per la codifica predittiva, che ipotizza tale integrazione come meccanismo di minimizzazione degli errori di previsione. Secondo la codifica predittiva questo meccanismo è caratterizzato dalle proprietà probabilistiche delle previsioni e dagli errori di previsione, come il livello di certezza o di precisione attribuito alle previsioni. Quindi, gli obiettivi di questo studio erano di etichettare simultaneamente i segnali dall’alto verso il basso e dal basso verso l’alto, di identificare un marcatore neurale diretto per l’integrazione di questi segnali durante la percezione visiva e, inoltre, di esaminare se, e come, tale marcatore è modulato dalla forza delle aspettative precedenti.
Al fine di differenziare i segnali top-down relativi alle previsioni, i segnali bottom-up relativi all’accumulo di input sensoriali e l’interazione tra tali segnali, abbiamo sviluppato il paradigma dell’Hierarchical Frequency Tagging (HFT) in cui due metodi di frequency tagging sono combinati nel dominio visivo in modo gerarchico. Per tracciare preferenzialmente i segnali dall’alto verso il basso (cioè i segnali di previsione presunta) abbiamo usato il wavelet semantico induced frequency tagging (SWIFT) che ha dimostrato di attivare costantemente le aree visive di basso livello e di coinvolgere periodicamente le aree visive di alto livello (quindi, selettivamente, tagging delle aree visive di alto livello;[Koenig-Robert e VanRullen, 2013; Koenig-Robert et al., 2015]). Per tracciare simultaneamente i segnali dal basso verso l’alto abbiamo usato la classica marcatura in frequenza, o i cosiddetti potenziali evocati visivi allo stato stazionario (SSVEP)(Norcia et al., 2015; Vialatte et al., 2010). Abbiamo combinato i due metodi presentando immagini modulate SWIFT a 1,3 HZ mentre modulavamo la luminanza globale dello stimolo a 10 Hz per suscitare SSVEP (Vedi Materiali e metodi per i dettagli). Criticamente, abbiamo ipotizzato che i componenti dell’intermodulazione (IM) apparissero come un marker di integrazione tra questi segnali differenziati.
L’intermodulazione è un fenomeno comune che si manifesta nei sistemi non lineari. Quando il segnale di ingresso è composto da più di una frequenza fondamentale (per esempio, F1 e F2) che interagiscono all’interno di un sistema non lineare, l’uscita di risposta mostrerà frequenze aggiuntive come combinazioni lineari delle frequenze di ingresso (per esempio, f1+f2, f1 – f2, ecc.) (si noti che in tutto il documento si indicano le frequenze di stimolo con lettere maiuscole (per esempio, F1) e le frequenze di risposta con lettere minuscole (per esempio, f1)). I componenti di intermodulazione nelle registrazioni EEG sono stati utilizzati per studiare le interazioni non lineari nel sistema visivo(Clynes, 1961; Regan e Regan, 1988; Zemon e Ratliff, 1984), con alcune recenti applicazioni per lo studio di sistemi di riconoscimento ad alto livello di oggetti visivi(Boremanse et al., 2013; Gundlach e Müller, 2013; Zhang et al., 2011). Invece di etichettare due segnali “dal basso verso l’alto”, tuttavia, il nostro paradigma è stato progettato per consentire l’esame dell’integrazione tra gli ingressi sia dal basso verso l’alto che dall’alto verso il basso nelle aree visuali inferiori.
L’inferenza percettiva ottimale si basa sulla nostra capacità di tener conto delle proprietà statistiche degli stimoli e del contesto in cui si verificano. Una di queste proprietà è l’aspettativa, che riflette il continuo processo di apprendimento probabilistico di ciò che è possibile o probabile nel prossimo ambiente sensoriale(Summerfield e Egner, 2009) e quindi gioca un ruolo centrale nella codifica predittiva. Infatti, diversi studi hanno dimostrato la relazione tra la prevedibilità degli stimoli e le risposte neurali(Kok et al., 2012a, Todorovic et al., 2011). Di conseguenza, abbiamo ipotizzato che manipolare la prevedibilità, o, come la definiamo noi, il livello di certezza sugli stimoli modulerebbe le risposte degli IM. La certezza è stata manipolata cambiando la frequenza delle immagini in ogni prova; più l’immagine viene presentata con frequenza, più è facile prevedere con successo quale sarà il prossimo stimolo.
Dal punto di vista dell’aggiornamento delle credenze bayesiane, l’aggiornamento delle credenze avviene combinando le previsioni derivate dalle probabilità precedenti con i dati sensoriali, con il risultato di errori di previsione che vengono ponderati in base alle loro precisioni relative(Mathys et al., 2014). La manipolazione della certezza ha quindi influito sulla precisione delle previsioni in modo tale che una maggiore certezza significa una maggiore precisione a priori e una minore ponderazione dell’errore di previsione dal basso verso l’alto. La precisione degli stimoli stessi (ad es. il livello di rumore nello stimolo) non variava da una prova all’altra.
Nel complesso, il nostro obiettivo era quindi quello di trovare non solo marcatori neurali per l’integrazione di segnali guidati dai sensori e dalla previsione, ma anche di esaminare come questo processo è modulato dalla certezza – un elemento centrale nel quadro della codifica predittiva.
Risultati
Ai partecipanti è stato presentato un “filmato” di 50 s, in cui una casa o un’immagine del volto è apparsa brevemente alla frequenza di 1,3 Hz (F2). Ogni prova di 50 s è stata costruita utilizzando un volto e un’immagine di una casa selezionati in modo casuale da un pool di immagini. Le immagini sono state criptate utilizzando due metodi di tagging di frequenza – SWIFT e SSVEP – che differenziano le aree nella gerarchia corticale(Figura 1). Prima di ogni prova, i partecipanti sono stati istruiti a contare il numero di volte in cui una delle due immagini è apparsa nella prova (la casa o l’immagine del volto) e hanno riportato la loro risposta alla fine di ogni prova. La proporzione di immagini è cambiata nel corso delle prove, da quelle in cui entrambe le immagini sono apparse in quasi la metà dei cicli (chiamate prove a ‘bassa certezza’) a quelle in cui una delle immagini è apparsa in quasi tutti i cicli (chiamate prove ad ‘alta certezza’).10.7554/eLife.22749.002Figure 1.Stimuli construction.Illustrazione schematica della costruzione degli stimoli.(A) Nel paradigma sono stati utilizzati un pool di 28 immagini di volti e 28 immagini di case (immagini con “liberi di usare, condividere o modificare, anche commercialmente” i diritti d’uso, ottenute da Google Images).(B) Il principio SWIFT. Il rimescolamento ciclico locale-contorno nel dominio wavelet ci permette di modulare la semantica dell’immagine ad una data frequenza (cioè la frequenza di marcatura, F2 = 1.3 hz, illustrato dalla linea rossa) mantenendo costanti nel tempo gli attributi fisici principali di basso livello (illustrati dalla linea blu)(C) Ogni prova (50 s) è stata costruita utilizzando un ciclo SWIFT (~769 ms) di un’immagine del volto scelta casualmente (rettangolo solido blu) e un ciclo SWIFT di un’immagine della casa scelta casualmente (rettangolo solido arancione). Per ogni ciclo SWIFT, è stato creato un corrispondente ciclo SWIFT “noise” basato su uno dei fotogrammi criptati del ciclo SWIFT originale (rettangolo arancione e blu tratteggiato). La sovrapposizione dei cicli SWIFT originali (rettangoli pieni) e del rumore (rettangoli tratteggiati) garantisce proprietà fisiche locali principali simili in tutti i frame SWIFT, indipendentemente dall’immagine che appare in ogni ciclo.(D) I due cicli SWIFT (casa e volto) sono stati presentati ripetutamente in un ordine pseudo-casuale per un totale di 65 cicli. La prova risultante è stata un filmato di 50 s in cui le immagini hanno raggiunto un picco ciclico (F2 = 1,3 Hz). Infine, una modulazione di contrasto sinusoidale globale a F1 = 10 Hz è stata applicata su tutto il filmato per evocare il SSVEP.DOI:http://dx.doi.org/10.7554/eLife.22749.002
Avendo assicurato che i partecipanti erano in grado di svolgere il compito (Figura 6), abbiamo prima verificato se i nostri due metodi di marcatura della frequenza erano effettivamente in grado di trascinare l’attività cerebrale e se potevamo osservare i componenti dell’intermodulazione (IM). La Figura 2 mostra i risultati della trasformata veloce di Fourier (FFT) mediati su tutti i 64 elettrodi, prove e partecipanti (N = 17). È importante notare che si possono osservare picchi significativi sia alle frequenze di marcatura (f1 = 10 Hz e f2 = 1,3 Hz) che alle loro armoniche (n1f1 e n2f2 dove n1 = 1,2 e n2 = 1,2,3…8 e 11; linee continue rosse e rosa nella figura 2) e in vari componenti del GI (n1f1 + n2f2 dove n1 = 1, n2 = +-1,+-2,+-3,+-4 e n1 = 2, n2 = -1,+2; linee tratteggiate arancioni nella figura 2) (un campione t-test, corretto con FDR p<0 .01 per frequenze di interesse nell’intervallo 1 Hz-40Hz).10.7554/eLife.22749.003Figure 2.Amplitude SNR spectra.Amplitude SNRs (vedi Materiali e metodi per la definizione di SNR), mediati su tutti gli elettrodi, prove e partecipanti, sono mostrati per frequenze fino a 23 Hz. I picchi possono essere visti alle frequenze di marcatura, alle loro armoniche e alle componenti IM. Le linee rosse solide segnano la frequenza SSVEP e la sua armonica (10 Hz e 20 Hz, entrambe con SNR significativamente maggiori di una). Le linee rosa piene segnano la frequenza SWIFT e le sue armoniche con SNRs significativamente maggiori di una (n2f2 dove n2 = 1,2,3…8 e 11). Le linee nere piene segnano le armoniche SWIFT con SNR non significativamente maggiori di una. Le linee tratteggiate gialle segnano le componenti IM con SNRs significativamente maggiori di una (n1f1 + n2f2; n1 = 1, n2 = +-1,+-2,+-3,+-4 e n1 = 2, n2 = -1,+2) e le linee tratteggiate nere segnano le componenti IM con SNRs non significativamente maggiori di una.DOI:http://dx.doi.org/10.7554/eLife.22749.003
Dopo aver stabilito che sia le frequenze di marcatura che le loro componenti di IM sono presenti nei dati, abbiamo esaminato la loro distribuzione spaziale sul cuoio capelluto, calcolata come media di tutte le prove. Ci aspettavamo di trovare le ampiezze SSVEP più forti sulla regione occipitale (poiché la corteccia visiva primaria è nota per essere una fonte principale di SSVEP[Di Russo et al., 2007]) e le ampiezze SWIFT più forti su regioni più temporali e parietali (poiché è stato dimostrato che SWIFT attiva sempre più aree più alte nel percorso visivo[Koenig-Robert et al., 2015]). I componenti IM, invece, dovrebbero provenire da unità di elaborazione locali che elaborano sia gli ingressi SSVEP che SWIFT. Nel quadro della codifica predittiva, le previsioni sono proiettate ai livelli più bassi della gerarchia corticale, dove sono integrate con gli input sensoriali. Abbiamo quindi ipotizzato che i segnali IM si troveranno principalmente nelle regioni occipitali.
I rapporti segnale-rumore di ampiezza SSVEP (SNR) erano più forti, come previsto, sulla regione occipitale (Figura 3A). Per SWIFT, i più alti SNRs sono stati trovati su più elettrodi temporali e centro-parietali(Figura 3B). I valori SNR più elevati per i componenti IM sono stati effettivamente riscontrati sugli elettrodi occipitali(Figura 3C). Per quantificare meglio la somiglianza tra le distribuzioni del cuoio capelluto delle frequenze SSVEP, SWIFT e IM abbiamo esaminato le correlazioni tra i valori SNR su tutti i 64 canali. Abbiamo poi esaminato se i coefficienti di correlazione per il confronto tra gli IM e il SSVEP erano superiori ai coefficienti di correlazione per il confronto tra gli IM e SWIFT. A tal fine abbiamo applicato la trasformazione r to z di Fisher ed eseguito un test Z per la differenza tra le correlazioni. Abbiamo scoperto che le distribuzioni di tutti i componenti IM erano significativamente più correlate con l’SSVEP che con la distribuzione SWIFT (z = 6,44, z = 5,52, z = 6.5 e z = 6,03 per f1+f2, f1-f2, f1+2f2 e f1-2f2, rispettivamente; a due code, FDR corretto p<0,01 per tutti i confronti; Figura 3-figure supplement 1).10.7554/eLife.22749.004Figure 3.Scalp distributions.Topography maps (log2(SNR)) per SSVEP (f1 = 10 Hz) (A), SWIFT(f2 = 1,3 Hz) (B), e quattro componenti IM (f1+f2, f1-f2, f1+2f2 e f1-2f1) (C). Gli SSVEP SNR erano generalmente più forti degli SWIFT SNR, che a loro volta erano più forti degli IM SNR (si noti la diversa scala delle barre dei colori).DOI:http://dx.doi.org/10.7554/eLife.22749.00410.7554/eLife.22749.005Figure 3-figure supplement 1.Per misurare la somiglianza tra le distribuzioni del cuoio capelluto delle frequenze SSVEP, SWIFT e IM, abbiamo esaminato la correlazione di Pearson tra i valori medi SNR tra i partecipanti per le frequenze IM, SSVEP e SWIFT su tutti i 64 canali (ogni punto rappresenta la media SNR per un singolo canale su 17 partecipanti).Per esaminare se i coefficienti di correlazione per il confronto tra i GI e il SSVEP erano superiori ai coefficienti di correlazione per il confronto tra i GI e lo SWIFT, abbiamo applicato la trasformazione r to z di Fisher ed eseguito un test Z per la differenza tra le correlazioni. Abbiamo scoperto che le distribuzioni di tutti i componenti del IM erano più altamente correlate con l’SSVEP che con la distribuzione SWIFT (z = 6,44, z = 5.52, z = 6,5 e z = 6,03 per f1 +f2, f1-f2, f1 +2f2 e f1-2f2, rispettivamente; a due code, FDR corretto p<0,01 per tutti i confronti).DOI:http://dx.doi.org/10.7554/eLife.22749.005
Come ulteriormente dettagliato nella Discussione, suggeriamo che questo risultato è coerente con l’idea che i segnali top-down (come taggati con SWIFT) sono proiettati verso le aree occipitali, dove sono integrati con segnali marcati SSVEP.
La fase finale della nostra analisi è stata quella di esaminare l’effetto della certezza sui segnali SSVEP, SWIFT e IM. Se le componenti IM osservate nei nostri dati riflettono un processo percettivo in cui i segnali sensoriali dal basso verso l’alto si integrano in modo non lineare con le previsioni dall’alto verso il basso, dovremmo aspettarci che siano modulati dal livello di certezza sui prossimi stimoli (in questo caso, se il prossimo stimolo sarà un volto o un’immagine della casa). Per testare questa ipotesi abbiamo modulato i livelli di certezza attraverso le prove variando la proporzione di immagini di case e volti presentati.
Utilizzando test di likelihood ratio con modelli lineari misti (vedi Materiali e metodi) abbiamo scoperto che la certezza ha avuto un effetto diverso sui segnali SSVEP, SWIFT e IM (Figure 4e 5).10.7554/eLife.22749.006Figure 4.Summary of the linear mixed-effects (LME) modelling.Abbiamo usato LME per esaminare il significato dell’effetto di certezza per SSVEP (f1 = 10 Hz), SWIFT (f2 = 1,3 Hz) e IM (separatamente per f1-2f2, f1-f2, f1+f2, f1+f2, e f1+2f2, così come attraverso tutti e quattro i componenti) registrati da elettrodi posteriori ROI. La tabella elenca la direzione degli effetti, il valore χ2 e il valore p corretto per FDR dai test del likelihood ratio (vedere Materiali e metodi).DOI:http://dx.doi.org/10.7554/eLife.22749.00610.7554/eLife.22749.007Figure5.Modulazione in base alla certezza.Bar trame di intensità del segnale (log di SNR, media su 30 canali posteriori e 17 partecipanti) in funzione dei livelli di certezza per SSVEP (A), SWIFT(B) e IMs (media tra i 4 componenti IM)(C). Le linee rosse mostrano le regressioni lineari per ogni categoria di frequenza. Le pendenze che sono significativamente diverse da 0 sono contrassegnate da asterischi rossi (** per p<0,001). Mentre per l’SSVEP non è stato rilevato alcun effetto principale significativo di certezza (p>0,05), per lo SWIFT è stata rilevata una significativa pendenza negativa, mentre per l’IM è stata rilevata una significativa pendenza positiva. Le barre di errore sono SEM tra i partecipanti. In basso) Le topo-plotterie, mediate tra i partecipanti, per bassa certezza (media tra i cassonetti 1-3), media certezza (media tra i cassonetti 4-7) e alta certezza (media tra i cassonetti 8-10) sono mostrate per SSVEP (A), SWIFT (B) e IM (media tra i 4 componenti dell’IM) (C).DOI:http://dx.doi.org/10.7554/eLife.22749.007
In primo luogo, SSVEP (log di SNR a f1 = 10 Hz) non è stato modulato in modo significativo dalla certezza (tutti i valori del Chi quadrato e p sono mostrati in Figura 4). Questo risultato è coerente con l’interpretazione dell’SSVEP in quanto riflette principalmente l’elaborazione visiva di basso livello che dovrebbe essere per lo più non influenzata dal grado di certezza dei segnali in ingresso.
In secondo luogo, i segnali SWIFT (log di SNR a f2 = 1,3 Hz) sono diminuiti significativamente nelle prove con maggiore certezza. Ciò è coerente con un’interpretazione dello SWIFT come correlato all’origine dei segnali top-down che sono modulati con certezza. In particolare, una migliore e più certa previsione porterebbe a una minore ponderazione dell’errore di previsione e quindi a minori revisioni della rappresentazione semantica ad alto livello.
In modo critico, i segnali IM sono risultati aumentare in funzione di una maggiore certezza per tre delle quattro componenti IM (f1-2f2 = 7,4 Hz, f1-f2 = 8,7 Hz, e f1+2f2 = 12,6 Hz, anche se non per f1+f2 = 11,3 Hz; Figura 4). L’effetto è rimasto altamente significativo anche quando si sono inclusi tutti e quattro i componenti del GI in un unico modello. In effetti, questo è l’effetto che ci si aspetterebbe di trovare se i GI riflettessero l’efficacia dell’integrazione tra i segnali dall’alto verso il basso, basati sulla previsione, e l’ingresso sensoriale dal basso verso l’alto. Nelle prove ad alta precisione la stessa immagine è apparsa nella maggior parte dei cicli, consentendo la migliore corrispondenza complessiva tra le previsioni e i segnali sensoriali bottom-up.
Inoltre, abbiamo trovato interazioni significative tra il livello di certezza e le diverse categorie di frequenza (SSVEP/SWIFT/IM). La pendenza di certezza era significativamente più alta per l’IM che per SSVEP (χ2 = 12,49, p<0,001) e significativamente più bassa per SWIFT che per SSVEP (χ2 = 64,45, p<0,001).

Figura 1.Stimoli di costruzione.Illustrazione schematica della costruzione degli stimoli.(A) Nel paradigma sono stati utilizzati un pool di 28 immagini di volti e 28 immagini di case (immagini con “liberi di usare, condividere o modificare, anche commercialmente” i diritti d’uso, ottenute da Google Images).(B) Il principio SWIFT. Il rimescolamento ciclico locale-contorno nel dominio wavelet ci permette di modulare la semantica dell’immagine a una data frequenza (cioè la frequenza di marcatura, F2 = 1.3 hz, illustrato dalla linea rossa) mantenendo costanti nel tempo gli attributi fisici principali di basso livello (illustrati dalla linea blu)(C) Ogni prova (50 s) è stata costruita utilizzando un ciclo SWIFT (~769 ms) di un’immagine del volto scelta casualmente (rettangolo solido blu) e un ciclo SWIFT di un’immagine della casa scelta casualmente (rettangolo solido arancione). Per ogni ciclo SWIFT, è stato creato un corrispondente ciclo SWIFT “noise” basato su uno dei fotogrammi criptati del ciclo SWIFT originale (rettangolo arancione e blu tratteggiato). La sovrapposizione dei cicli SWIFT originali (rettangoli pieni) e del rumore (rettangoli tratteggiati) garantisce proprietà fisiche locali principali simili in tutti i frame SWIFT, indipendentemente dall’immagine che appare in ogni ciclo.(D) I due cicli SWIFT (casa e volto) sono stati presentati ripetutamente in un ordine pseudo-casuale per un totale di 65 cicli. La prova risultante è stata un filmato di 50 s in cui le immagini hanno raggiunto un picco ciclico (F2 = 1,3 Hz). Infine, una modulazione di contrasto sinusoidale globale a F1 = 10 Hz è stata applicata su tutto il filmato per evocare il SSVEP.DOI:
http://dx.doi.org/10.7554/eLife.22749.002

Figura 2.Spettri SNR di ampiezza.Gli spettri di ampiezza SNR (vedi Materiali e metodi per la definizione di SNR), mediati su tutti gli elettrodi, prove e partecipanti, sono mostrati per frequenze fino a 23 Hz. I picchi sono visibili alle frequenze di marcatura, alle loro armoniche e alle componenti IM. Le linee rosse solide segnano la frequenza SSVEP e la sua armonica (10 Hz e 20 Hz, entrambe con SNR significativamente maggiori di una). Le linee rosa piene segnano la frequenza SWIFT e le sue armoniche con SNRs significativamente maggiori di una (n2f2 dove n2 = 1,2,3…8 e 11). Le linee nere piene segnano le armoniche SWIFT con SNR non significativamente maggiori di una. Le linee tratteggiate gialle segnano le componenti IM con SNRs significativamente maggiori di una (n1f1 + n2f2; n1 = 1, n2 = +-1,+-2,+-3,+-4 e n1 = 2, n2 = -1,+2) e le linee tratteggiate nere segnano le componenti IM con SNRs non significativamente maggiori di una.DOI:
http://dx.doi.org/10.7554/eLife.22749.003
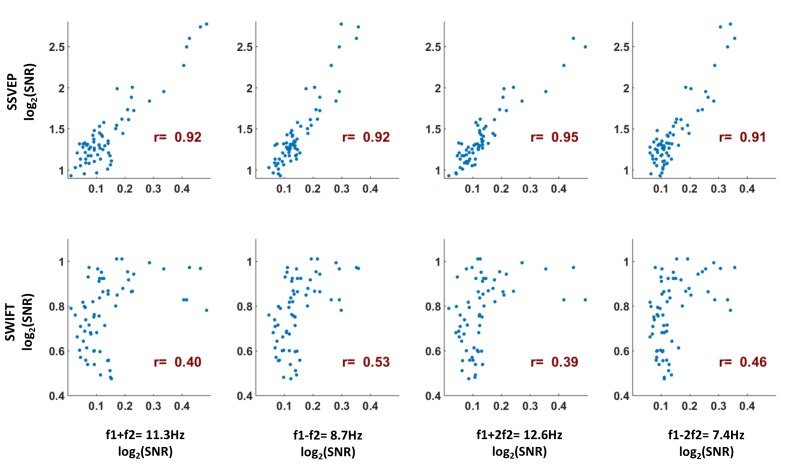
Figura 3-figure supplement 1.Come misura della somiglianza tra le distribuzioni del cuoio capelluto delle frequenze SSVEP, SWIFT e IM, abbiamo esaminato la correlazione di Pearson tra i valori medi SNR tra i partecipanti per le frequenze IM, SSVEP e SWIFT su tutti i 64 canali (ogni punto rappresenta la media SNR per un singolo canale su 17 partecipanti).Mappe topografiche (log2(SNR)) per SSVEP (f1 = 10 Hz) (A), SWIFT(f2 = 1,3 Hz) (B), e quattro componenti IM (f1+f2, f1-f2, f1+2f2 e f1-2f1) (C). Gli SSVEP SNR erano generalmente più forti degli SWIFT SNR, che a loro volta erano più forti degli IM SNR (si noti la diversa scala delle barre dei colori).DOI:
http://dx.doi.org/10.7554/eLife.22749.004Per esaminare se i coefficienti di correlazione per il confronto tra i GI e il SSVEP erano superiori ai coefficienti di correlazione per il confronto tra i GI e lo SWIFT, abbiamo applicato la trasformazione r to z di Fisher ed eseguito un test Z per la differenza tra le correlazioni. Abbiamo scoperto che le distribuzioni di tutti i componenti del IM erano più altamente correlate con l’SSVEP che con la distribuzione SWIFT (z = 6,44, z = 5.52, z = 6,5 e z = 6,03 per f1 +f2, f1-f2, f1 +2f2 e f1-2f2, rispettivamente; a due code, FDR corretto p<0,01 per tutti i confronti).DOI:
http://dx.doi.org/10.7554/eLife.22749.005

Figura 3-figure supplement 1.Come misura della somiglianza tra le distribuzioni del cuoio capelluto delle frequenze SSVEP, SWIFT e IM, abbiamo esaminato la correlazione di Pearson tra i valori medi SNR tra i partecipanti per le frequenze IM, SSVEP e SWIFT su tutti i 64 canali (ogni punto rappresenta la media SNR per un singolo canale su 17 partecipanti).Per esaminare se i coefficienti di correlazione per il confronto tra i GI e il SSVEP erano superiori ai coefficienti di correlazione per il confronto tra i GI e lo SWIFT, abbiamo applicato la trasformazione r to z di Fisher ed eseguito un test Z per la differenza tra le correlazioni. Abbiamo scoperto che le distribuzioni di tutti i componenti del IM erano più altamente correlate con il SSVEP che con la distribuzione SWIFT (z = 6,44, z = 5.52, z = 6,5 e z = 6,03 per f1 +f2, f1-f2, f1 +2f2 e f1-2f2, rispettivamente; a due code, FDR corretto p<0,01 per tutti i confronti).DOI:
http://dx.doi.org/10.7554/eLife.22749.005
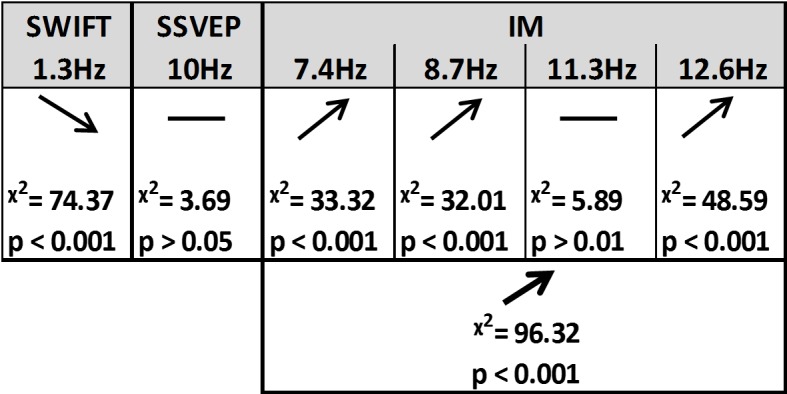
Figura 4.Sintesi della modellazione lineare a effetti misti (LME).Abbiamo usato LME per esaminare il significato dell’effetto di certezza per SSVEP (f1 = 10 Hz), SWIFT (f2 = 1,3 Hz) e IM (separatamente per f1-2f2, f1-f2, f1+f2, e f1+2f2, così come attraverso tutti e quattro i componenti) registrati da elettrodi posteriori ROI. La tabella elenca la direzione degli effetti, il valore χ2 e il valore p corretto per FDR dai test del likelihood ratio (vedi Materiali e metodi).DOI:
http://dx.doi.org/10.7554/eLife.22749.006

Figura 5.Modulazione per certezza.Trame a barre della potenza del segnale (log di SNR, media su 30 canali posteriori e 17 partecipanti) in funzione dei livelli di certezza per SSVEP (A), SWIFT(B) e IM (media dei 4 componenti dell’IM)(C). Le linee rosse mostrano le regressioni lineari per ogni categoria di frequenza. Le pendenze che sono significativamente diverse da 0 sono contrassegnate da asterischi rossi (** per p<0,001). Mentre per l’SSVEP non è stato rilevato alcun effetto principale significativo di certezza (p>0,05), per lo SWIFT è stata rilevata una significativa pendenza negativa, mentre per l’IM è stata rilevata una significativa pendenza positiva. Le barre di errore sono SEM tra i partecipanti. In basso) Le topo-plotterie, mediate tra i partecipanti, per bassa certezza (media tra i cassonetti 1-3), media certezza (media tra i cassonetti 4-7) e alta certezza (media tra i cassonetti 8-10) sono mostrate per SSVEP (A), SWIFT (B) e IM (media tra i 4 componenti dell’IM) (C).DOI:
http://dx.doi.org/10.7554/eLife.22749.007
Discussione
La chiave della percezione è la capacità di integrare informazioni neurali derivate da diversi livelli della gerarchia corticale(Fahrenfort et al., 2012; Tononi e Edelman, 1998). L’obiettivo di questo studio è stato quello di identificare i marcatori neurali per l’integrazione tra i segnali dall’alto verso il basso e dal basso verso l’alto nell’inferenza percettiva, e di esaminare come questo processo sia modulato dal livello di certezza degli stimoli. Hierarchical Frequency Tagging combina i metodi SSVEP e SWIFT che hanno dimostrato di etichettare prevalentemente livelli bassi (V1/V2) e livelli più alti, semanticamente ricchi nella gerarchia visiva, rispettivamente. Abbiamo ipotizzato che questi segnali riflettano i segnali sensoriali dal basso verso l’alto (o gli errori di previsione) e le previsioni dall’alto verso il basso. Criticamente, abbiamo considerato i componenti dell’intermodulazione (IM) come un indicatore dell’integrazione tra questi segnali e abbiamo ipotizzato che essi riflettano il livello di integrazione tra le previsioni dall’alto verso il basso (di diversi punti di forza manipolati dalla certezza) e gli input sensoriali dal basso verso l’alto.
Abbiamo trovato un’etichettatura di frequenza significativa sia per i segnali SSVEP e SWIFT, sia per vari componenti IM(Figura 2). Ciò conferma la nostra capacità di utilizzare contemporaneamente due metodi di tagging in un unico paradigma e, cosa più importante, fornisce la prova dell’integrazione corticale dei segnali taggati SWIFT e SSVEP. In effetti, la topografia del cuoio capelluto per le tre categorie di frequenza (SSVEP, SWIFT e IM) era, come si vedrà più avanti, in gran parte coerente con le nostre ipotesi(Figura 3) e, cosa importante, differivano tutte per il modo in cui erano modulate dal livello di certezza relativo agli stimoli futuri. Mentre i segnali SSVEP non sono stati modulati in modo significativo dalla certezza, i segnali SWIFT sono diminuiti e i segnali IM sono aumentati in funzione dell’aumento della certezza(Figura 5). Nella discussione che segue esaminiamo come i nostri risultati supportano il quadro di codifica predittiva.
Il quadro di codifica predittiva per la percezione
La nozione di inferenza percettiva e l’attenzione alle aspettative precedenti risale a Ibn al Haytham nell’XI secolo, il quale osservava che “molte proprietà visibili sono percepite dal giudizio e dall’inferenza oltre a percepire la forma dell’oggetto” (Sabra, 1989). I racconti contemporanei della percezione trattano queste idee in termini di inferenza bayesiana e di codifica predittiva(Friston, 2005, 2009; Hohwy, 2013; Clark, 2013; Friston e Stephan, 2007). Nel quadro della codifica predittiva, le ipotesi sullo stato del mondo esterno si formano sulla base dell’esperienza precedente. Le previsioni sono generate da queste ipotesi, che sono poi proiettate ai livelli più bassi della gerarchia corticale, e continuamente testate e regolate alla luce delle informazioni in arrivo, guidate dagli stimoli. In effetti, il ruolo dei segnali dall’alto verso il basso nella percezione è stato dimostrato sia negli studi sugli animali che sull’uomo(Hupe et al., 1998, Pascual-Leone e Walsh, 2001). Gli elementi dell’input sensoriale che non possono essere spiegati con le attuali previsioni dall’alto verso il basso sono indicati come errore di previsione (PE). Questo PE è suggerito come il segnale (ponderato con precisione) dal basso verso l’alto che si propaga dai livelli più bassi a quelli più alti della gerarchia corticale fino a quando non può essere spiegato, consentendo successive revisioni di parti di livello superiore delle ipotesi complessive. La nozione di PE è stata convalidata da numerosi studi(Hughes et al., 2001; Kellermann et al., 2016; Lee e Nguyen, 2001; Todorovic et al., 2011; Wacongne et al., 2011) e diversi studi suggeriscono che i segnali top-down e bottom-up possono essere differenziati in termini di bande di frequenza oscillatorie tipiche(Fontolan et al., 2014; Sedley et al., 2016; Sherman et al., 2016; Michalareas et al., 2016; Mayer et al., 2016). La percezione, nel quadro della codifica predittiva, si ottiene attraverso un processo iterativo che individua l’ipotesi che meglio minimizza l’errore complessivo di previsione su più livelli della gerarchia corticale, tenendo conto dell’apprendimento precedente, del contesto più ampio e delle stime di precisione(Friston, 2009). L’integrazione costante delle informazioni neurali dal basso verso l’alto e dall’alto verso il basso è quindi intesa come un elemento cruciale nella percezione(Fahrenfort et al., 2012; Friston, 2005; Tononi e Edelman, 1998).
SSVEP, SWIFT e la loro modulazione per certezza
Il metodo SSVEP prevalentemente attività tags in bassi livelli della gerarchia visiva e in effetti più alto SSVEP SNRs sono stati misurati nel nostro progetto su elettrodi occipitali(Figura 3). Abbiamo dimostrato che il segnale SSVEP non è stato significativamente modulato dalla certezza(Figura 5A). Questi risultati suggeriscono che il SSVEP riflette persistente ingresso sensoriale dal basso verso l’alto, che non dipende fortemente dalle previsioni top-down che si verificano alla frequenza SWIFT.
Il metodo SWIFT, al contrario, ha dimostrato di taggare sempre più aree più alte lungo il percorso visivo che elaborano le informazioni semantiche(Koenig-Robert et al., 2015), e abbiamo effettivamente trovato più alto SWIFT SNRs SWIFT su più elettrodi temporali e parietali(Figura 3). Poiché l’attivazione di queste aree dipende dal riconoscimento dell’immagine(Koenig-Robert e VanRullen, 2013), abbiamo ipotizzato che, contrariamente al SSVEP, il segnale SWIFT dovrebbe mostrare una maggiore dipendenza dalla certezza. In effetti, abbiamo osservato che SWIFT SNR è diminuito con l’aumento dei livelli di certezza(Figura 5B).
Un’interpretazione di questo risultato è che riflette il peso decrescente sui segnali PE in condizioni di elevata certezza (che a loro volta guidano le successive previsioni dall’alto verso il basso). La nozione di certezza qui usata è ben colta nel lavoro sul Filtro Gaussiano Gerarchico(Mathys et al., 2014): “…ha senso che l’aggiornamento dovrebbe essere antiproporzionale [alla precisione della convinzione sul livello da aggiornare] poiché più l’agente è certo di conoscere il vero valore …, meno incline dovrebbe essere a modificarlo” (per una formulazione matematica, vedi eq. 56 in quel lavoro, e, per il caso gerarchico e che produce un tasso di apprendimento variabile, eq. 59). In effetti, vari studi hanno già dimostrato che gli stimoli altamente prevedibili tendono ad evocare risposte neurali ridotte(Alink et al., 2010; Todorovic e de Lange, 2012; Todorovic et al., 2011). Poiché i PE riflettono gli elementi di input sensoriali che non possono essere spiegati con le previsioni, tali risposte neurali ridotte sono state suggerite per riflettere la diminuzione dei segnali di PE(Todorovic et al., 2011).
Il declino SWIFT SNR può essere descritto con certezza anche in termini di adattamento neurale (o soppressione della ripetizione), cioè la riduzione della risposta neurale evocata misurata alla ripetizione dello stesso stimolo o quando lo stimolo è altamente previsto. Nel nostro studio attuale, le prove ad alta tenuta contenevano più cicli consecutivi in cui la stessa immagine è stata presentata, quindi ci si aspetta che l’adattamento si verifichi. Dal punto di vista della codifica predittiva, tuttavia, l’adattamento è spiegato in termini di crescente precisione delle previsioni derivanti dall’apprendimento percettivo(Auksztulewicz e Friston, 2016; Friston, 2005; Henson , 2003). L’adattamento quindi “riflette una riduzione dell'”errore di predizione” percettivo… che si verifica quando l’evidenza sensoriale si conforma ad un più probabile (visto in precedenza), rispetto ad un meno probabile (romanzo), percept” (Summerfieldet al., 2008).
L’intermodulazione (IM) come marker dell’integrazione neurale dell’elaborazione top-down e bottom-up
Il marcatore di intermodulazione (IM) è stato impiegato perché lo studio della percezione richiede non solo la distinzione tra segnali dall’alto verso il basso e dal basso verso l’alto, ma anche l’esame dell’integrazione tra tali segnali. Di conseguenza, il punto di forza del paradigma dell’Hierarchical Frequency Tagging (HFT) sta nella sua potenziale capacità di ottenere, attraverso il verificarsi dell’IM, una misura elettrofisiologica diretta dell’integrazione tra segnali derivati da diversi livelli della gerarchia corticale.
Dal punto di vista più generale, la presenza di componenti IM implica semplicemente un’integrazione non lineare delle risposte stazionarie suscitate dalle manipolazioni SWIFT e SSVEP. Sono stati suggeriti vari circuiti neurali biologicamente plausibili per implementare operazioni neuronali non lineari(Kouh e Poggio, 2008), e tali dinamiche neuronali non lineari possono essere coerenti con un certo numero di modelli, che vanno dalle cascate di filtri non lineari in avanti (ad esempio, reti di convoluzione utilizzate nell’apprendimento profondo) fino alle architetture ricorrenti implicate dalla codifica predittiva. La presenza di GI di per sé non può quindi indicare in modo conclusivo specifici processi computazionali o neuronali su cui i GI potrebbero essere mappati. Suggerire i GI come prove per la codifica predittiva piuttosto che altre teorie della percezione rimane quindi in qualche modo indiretto, tuttavia, vari argomenti indicano in effetti la mediazione ricorrente e dall’alto verso il basso delle risposte dei GI nei nostri dati.
In primo luogo, le distribuzioni del cuoio capelluto dei componenti del GI erano più fortemente correlate alla distribuzione spaziale del SSVEP (f1 = 10 Hz) piuttosto che al SWIFT (f2 = 1,3 Hz) (Figura 3-figuresupplement 1). Questo schema supporta l’idea che i componenti IM nei nostri dati Hierarchical Frequency Tagging (HFT) riflettono l’integrazione dei segnali generati nelle aree contrassegnate da SWIFT che proiettano e sono integrate con i segnali generati ai livelli inferiori della corteccia visiva, come contrassegnati dal SSVEP. Questo naturalmente è coerente con il quadro di codifica predittiva in cui le previsioni generate ai livelli più alti della gerarchia corticale si propagano alle aree più basse della gerarchia, dove possono essere testate alla luce dei segnali sensoriali in entrata.
In secondo luogo, e cosa ancora più importante, gli SNR IM sono aumentati in funzione della certezza (contrariamente agli SNR SWIFT). Suggeriamo che questo risultato dia un supporto specifico al framework di codifica predittiva dove la traduzione delle previsioni in errori di previsione si basa su funzioni non lineari(Auksztulewicz e Friston, 2016). In effetti, le non linearità nei modelli di codifica predittiva sono un corollario specifico dei segnali modulatori top-down(Friston, 2005). Variando i livelli di certezza, come operazionalizzato nei nostri stimoli, ci si aspetterebbe quindi che l’intensità del segnale IM abbia un impatto sulla forza del segnale IM attraverso la modulazione non lineare dell’input bottom-up attraverso le previsioni top-down. In particolare, prove di certezza più elevate hanno indotto una maggiore prevedibilità delle immagini in arrivo e una maggiore corrispondenza complessiva per tutta la durata della prova tra previsioni e input sensoriali. L’aumento di SNR IM nei nostri dati può quindi riflettere l’integrazione efficiente o l’adattamento generale tra le previsioni e gli input sensoriali che ci si dovrebbe aspettare quando gran parte degli stimoli imminenti è altamente prevedibile.
Mappatura delle risposte HFT ai modelli di codifica predittiva
In linea con la nozione di cui sopra, è possibile suggerire una mappatura più specifica dei componenti HFT (SWIFT, SSVEP e IM) su elementi di codifica predittiva. Secondo il modello impostato da Auksztulewicz e Friston(Auksztulewicz e Friston, 2016), ad esempio, le non linearità dall’alto verso il basso (funzioni g e f nelle equazioni 6 e 7, così come nella figura 1 in quel lavoro) sono guidate da due elementi: (1) le aspettative condizionali delle cause nascoste (µ v,cioè la “migliore stima” del cervello su ciò che guida i cambiamenti nel mondo fisico), e (2) le aspettative condizionali degli stati nascosti (µ x, cioè la migliore stima del cervello sulla reale “fisica” del mondo esterno che guida le risposte degli organi sensoriali). Le relazioni tra le possibili “cause” e gli “stati” (ad esempio, come il movimento di una nuvola nel cielo impatta la luminanza degli oggetti a terra) vengono apprese nel tempo ed è il punto cruciale del modello dinamico generativo incarnato dal cervello. Facendo appello a questo modello, le aspettative condizionate di cause e stati nascosti possono essere suggerite come guidate principalmente da SWIFT (attività di tagging in aree ricche di informazioni semantiche) e SSVEP (attività di tagging in aree che rispondono a caratteristiche visive di basso livello), rispettivamente. Ci si può quindi aspettare che le previsioni dall’alto verso il basso portino alla formazione di componenti IM che riflettono l’integrazione non lineare dei segnali pilotati da SWIFT e SSVEP.
Un’ulteriore questione riguarda le potenziali interpretazioni quantitative dei GI e il loro aumento con certezza. Una di queste interpretazioni è che i GI codificano collettivamente (con una certa approssimazione rispetto al log) le prove del modello. Questa nozione è compatibile con la nostra interpretazione dei GI in termini di “adattamento” tra previsioni e input sensoriali. In questo caso, ci si aspetterebbe che i GI aumentino con certezza, come mostrato nella Figura 5c. È una domanda interessante per ulteriori ricerche se questa interpretazione dei GI come prova del modello di codifica può generare previsioni quantitative per la magnitudo dei GI in diverse manipolazioni sperimentali di SWIFT e SSVEP, e inoltre, se diversi GI potrebbero risultare da manipolazioni distinte di aspettative e precisioni.
Interpretazioni alternative per i componenti dell’IM
Si potrebbe potenzialmente sostenere che i nostri risultati di IM possono derivare solo dall’elaborazione sensoriale. Per esempio, si consideri una popolazione di neuroni confinata all’interno della corteccia visiva, in cui alcuni sono modulati dal contrasto dello stimolo tramite SSVEP e altri sono modulati dalle informazioni di categoria tramite SWIFT. Le interazioni tra questi neuroni, in un tale meccanismo essenzialmente feedforward, possono potenzialmente rappresentare la formazione di componenti IM anche senza segnali dall’alto verso il basso. Tuttavia, questa interpretazione alternativa non può facilmente tener conto del modello di cambiamenti reciproci che si trovano con certezza nei nostri dati (SWIFT decrescente e IM crescente). La sola integrazione di input sensoriali dal basso verso l’alto dovrebbe essere cieca rispetto alle proprietà probabilistiche della prova in modo tale che la contabilizzazione del modello di dati qui richiede di suggerire un meccanismo locale aggiuntivo che sia sensibile alla manipolazione della certezza. Pertanto, sembra più ragionevole ipotizzare un’interazione tra aree sensoriali precoci e superiori, che hanno dimostrato di essere sensibili alla prevedibilità degli stimoli(Kok et al., 2012a, Rauss et al., 2011).
Inoltre, le componenti IM potrebbero in linea di principio derivare dall’integrazione di segnali SSVEP a basso livello con segnali minimi, non semantici, guidati da SWIFT, intrappolati nella corteccia visiva precoce (ad esempio, mediante l’etichettatura residua delle componenti di rumore all’interno dei frame SWIFT). Anche se questa possibilità non può essere completamente esclusa, i risultati precedenti suggeriscono che SWIFT non tagga l’attività a livello V1 in quanto non è stato possibile rilevare alcuna attività di tagging né per le prove in cui sono stati utilizzati modelli non semantici né per le prove in cui l’attenzione è stata allontanata dall’immagine(Koenig-Robert e VanRullen, 2013; Koenig-Robert et al., 2015). Il basso livello residuo di SWIFT-tagging non è quindi probabile che sia il principale contributore dei componenti di IM che si trovano qui.
Diversi studi hanno dimostrato una relazione tra le componenti dell’IM e la percezione(Boremanse et al., 2013; Gundlach e Müller, 2013; Zhang et al., 2011). In tutti questi studi, l’aumento riportato della potenza del segnale IM riflette potenzialmente l’integrazione di diversi elementi di input all’interno di una singola rappresentazione neurale. Tuttavia, la forza dell’Hierarchical Frequency Tagging sta nella sua capacità di etichettare simultaneamente sia gli ingressi dal basso verso l’alto che quelli dall’alto verso il basso nelle aree visuali inferiori. I segnali IM, nel nostro paradigma, rifletterebbero quindi il punto cruciale della funzione di verifica delle ipotesi, ovvero il confronto tra segnali di previsione e segnali sensoriali, o l’integrazione tra unità di stato e unità di errore.
Manipolare la certezza attraverso l’apprendimento implicito
Un altro punto degno di nota è che la manipolazione della certezza che abbiamo usato in questo studio differisce da diversi altri studi (ad esempio[Kok et al., 2013; Kok et al., 2012a]) in cui l’aspettativa è esplicitamente manipolata con uno spunto precedente. In ciascuno degli studi attuali, i livelli di certezza sono stati appresi “online” in base alla proporzione di immagini che sono apparse in quello studio. Operazionalizzare la certezza in questo modo può aggiungere fonti di variabilità che non abbiamo controllato, come le differenze individuali nei tassi di apprendimento. D’altra parte, la convinzione sulla probabilità di un evento è spesso plasmata attraverso l’esposizione ripetuta allo stesso tipo di evento, dando maggiore validità ecologica al nostro progetto di studio. È una domanda interessante per ulteriori ricerche se la conoscenza a priori dei livelli di certezza darà origine a diversi GI, così come se le differenze individuali nei tassi di apprendimento (comprese ad esempio le differenze nella “dimenticanza ottimale”, [Mathyset al., 2014]) influenzano i GI.
Conclusione
Nel complesso, le prove che abbiamo presentato dimostrano plausibilmente la capacità della nuova tecnica HFT di ottenere una misura fisiologica diretta dell’integrazione delle informazioni derivate dai diversi livelli della gerarchia corticale durante la percezione. A sostegno del conto di codifica predittiva della percezione, i nostri risultati suggeriscono che i segnali etichettati dall’alto verso il basso e semanticamente taggati sono integrati con segnali guidati dal basso verso l’alto, e questa integrazione è modulata dal livello di certezza sulle cause dell’input percepito.
Materiali e metodi
Costruzione di stimoli
SSVEP e SWIFT
Negli studi di stato stazionario-visivo-evocato-potenziale (SSVEP), l’intensità (luminanza o contrasto) di uno stimolo è tipicamente modulata nel tempo ad una data frequenza, F Hz (cioè la “frequenza di marcatura”). Picchi alla frequenza di tagging-frequenza, f Hz, nello spettro del segnale registrato sono così intesi per riflettere l’attività neurale stimolo-driven. Tuttavia, l’uso di metodi SSVEP imporre alcune limitazioni per lo studio delle gerarchie percettive. Quando il contrasto o la luminanza di uno stimolo è modulato nel tempo, allora tutti i livelli della gerarchia visiva sono trascinati alla frequenza di marcatura. Così, diventa difficile dissociare l’etichettatura di frequenza relativa all’elaborazione di feature di basso livello da quella relativa alle rappresentazioni semantiche di alto livello.
Il tagging di frequenza indotto da wavelet semantico (SWIFT) supera questo ostacolo rimescolando le sequenze di immagini in modo da mantenere le caratteristiche fisiche di basso livello mentre modula le proprietà delle immagini di medio e alto livello. In questo modo, è stato dimostrato che SWIFT attiva costantemente le prime aree visive mentre esegue il tagging selettivo delle rappresentazioni di oggetti ad alto livello sia in EEG(Koenig-Robert e VanRullen, 2013) che in fMRI(Koenig-Robert et al., 2015).
Il metodo per la creazione delle sequenze SWIFT è descritto in dettaglio altrove(Koenig-Robert e VanRullen, 2013). In breve, le sequenze sono state create mediante la rimescolanza ciclica del wavelet nello spazio 3D delle onde, consentendo di rimescolare i contorni conservando gli attributi locali di basso livello come la luminanza, il contrasto e la frequenza spaziale. In primo luogo, le trasformazioni wavelet sono state applicate sulla base del wavelet discreto Meyer e di sei livelli di decomposizione. In ogni posizione e scala, il contorno locale è rappresentato da un vettore 3D. I vettori che puntano in direzioni diverse ma della stessa lunghezza del vettore originale rappresentano versioni diversamente orientate dello stesso contorno locale dell’immagine. Due di questi vettori aggiuntivi sono stati selezionati in modo casuale per definire un percorso circolare (mantenendo la lunghezza del vettore lungo il percorso). Il wavelet-scrambling ciclico è stato poi eseguito ruotando ogni vettore originale lungo il percorso circolare. La trasformazione wavelet inversa è stata poi utilizzata per ottenere le sequenze di immagini nel dominio dei pixel. Per costruzione, l’immagine originale non decodificata è apparsa una volta in ogni ciclo (1,3 Hz). L’immagine originale era identificabile brevemente intorno al picco dell’immagine incorporata (vedi Video 1, disponibile anche su https://figshare.com/s/44f1a26ecf55b6a35b2f), come è stato dimostrato psicofisicamente(Koenig-Robert et al., 2015).Video 1.A slow-motion representation of two SWIFT cycles.DOI:http://dx.doi.org/10.7554/eLife.22749.00810.7554/eLife.22749.008

Video 1.Una rappresentazione al rallentatore di due cicli SWIFT.2. DOI:
http://dx.doi.org/10.7554/eLife.22749.008
Prova SWIFT-SSVEP
Le sequenze SWIFT sono state create da un pool di immagini in scala di grigi di case e volti (28 ciascuna, scaricate da Internet utilizzando Google Images(https://www. google.com/imghp) per trovare immagini con diritti d’uso “liberi di usare, condividere o modificare, anche commercialmente”; Figura 1A-B ).
Ogni trial è stato costruito utilizzando una sequenza di case e una di volti, selezionati in modo casuale dal pool di sequenze (indipendentemente dagli altri trial). Utilizzando queste due sequenze, che, nel contesto di una prova completa ci riferiamo ai ‘cicli’ SWIFT, abbiamo creato un ‘filmato’ di 50 s contenente 65 cicli consecutivi ripetuti in ordine pseudorandom a F2 = 1,3 Hz (~769 ms per ciclo, Figura 1D). L’immagine identificabile al culmine di ogni ciclo era il volto o l’immagine della casa. Il metodo SWIFT è stato progettato per garantire che le proprietà visive locali di basso livello all’interno di ogni sequenza (ciclo) siano preservate in tutti i fotogrammi. Tuttavia, queste proprietà potevano differire significativamente tra le sequenze del volto e della casa, con la conseguente potenziale associazione dell’attività con il marchio SWIFT con le differenze nelle caratteristiche di basso livello tra i cicli del volto e della casa. Per evitare questo, abbiamo creato e unito ulteriori sequenze di “rumore” nel modo seguente: Per prima cosa, abbiamo selezionato uno dei frame criptati da ciascuna delle sequenze SWIFT originali (quello “più criptato”, cioè il frame più distante dall’immagine originale presentata al culmine del ciclo). Poi, abbiamo creato delle sequenze di rumore applicando il metodo SWIFT su ciascuno dei fotogrammi scrambled selezionati. In questo modo, ogni sequenza “immagine” originale aveva una sequenza di “rumore” corrispondente che corrispondeva alle proprietà di basso livello della sequenza di immagini. Infine, le sequenze ‘immagine’ erano alfa miscelate con le sequenze ‘rumore’ dell’altra categoria con peso uguale (Figura 1C,le sequenze di immagini sono circondate da quadrati solidi e le sequenze di rumore con quadrati tratteggiati). Per esempio, i cicli in cui doveva apparire un’immagine del volto contenevano la sequenza dell’immagine del volto sovrapposta ad una sequenza di rumore di casa(Figura 1C, lato destro). In questo modo, gli attributi visivi di basso livello generale erano costanti in tutti i fotogrammi della prova, indipendentemente dall’immagine identificabile in ogni ciclo.
Una modulazione di contrasto sinusoidale globale a F1 = 10 Hz è stata applicata su tutto il filmato per evocare l’SSVEP (vedi Video 2 e 3, disponibili anche su https://figshare.com/s/75aed271d32ba024d1ee).Video 2.Una rappresentazione animata di 8 s di film d’animazione di un trial HFT.DOI:http://dx.doi.org/10.7554/eLife.22749.00910.7554/eLife.22749.009Video3.Un’animazione al rallentatore dei primi cicli di un trial HFT.DOI:http://dx.doi.org/10.7554/eLife.22749.01010.7554/eLife.22749.010

Video 2.Un film d’animazione di 8 s di rappresentazione di un processo HFT.3. DOI:
http://dx.doi.org/10.7554/eLife.22749.009

Video 3.Un’animazione al rallentatore dei primi cicli all’interno di una prova HFT.4. DOI:
http://dx.doi.org/10.7554/eLife.22749.010
Partecipanti e procedura
Per questo studio sono stati testati in totale 27 partecipanti (12 femmine; età media = 28,9 anni, std = 6,6). I partecipanti hanno dato il loro consenso scritto a partecipare all’esperimento. Le dimensioni tipiche del campione negli studi SSVEP e SWIFT variano tra 8-22 partecipanti per gruppo sperimentale (Chicherove Herzog, 2015; Katyal et al., 2016; Koenig-Robert e VanRullen, 2013; Koenig-Robert et al., 2015; Painter et al., 2014). Poiché questo è il primo studio che combina simultaneamente i metodi di marcatura SWIFT e SSVEP, abbiamo voluto essere all’estremità superiore di questa gamma. Le procedure sperimentali sono state approvate dal Comitato etico per la ricerca umana della Monash University.
I partecipanti erano comodamente seduti con la testa sostenuta da una mentoniera a 50 cm dallo schermo (CRT, frequenza di aggiornamento di 120 HZ) in una stanza poco illuminata. Le sequenze sono state presentate al centro dello schermo su sfondo grigio e ai partecipanti è stato chiesto di mantenere la loro fissazione al centro del display. Ai partecipanti è stato chiesto di ridurre al minimo i lampeggiamenti o gli spostamenti durante ogni prova, ma sono stati incoraggiati a farlo se necessario nelle pause tra una prova e l’altra di 50 secondi. Ad ogni partecipante è stato presentato un totale di 56 di questi 50 s di prova. È importante notare che la proporzione di immagini della casa e del volto variava nel corso delle prove, coprendo l’intera gamma possibile (pseudorandomamente selezionate in modo tale che una particolare proporzione non si ripetesse all’interno di ogni partecipante). Ogni prova ha quindi variato il livello di certezza associato alle immagini future.
Per verificare che i partecipanti si impegnassero nel compito, prima di ogni prova appariva sullo schermo una frase che indicava loro di contare il numero di presentazioni della casa o del volto. Le prove sono iniziate quando il partecipante ha premuto la barra spaziatrice. Alla fine di ogni prova, alla fine di ogni prova, hanno usato la tastiera per inserire il numero di immagini contate. Queste risposte sono state registrate e utilizzate in seguito per escludere dall’analisi i partecipanti con prestazioni scadenti. Una pausa di riposo di 2-3 minuti è stata introdotta dopo ogni 14 prove. L’EEG continuo è stato acquisito da 64 elettrodi per cuoio capelluto utilizzando un sistema Brain Products BrainAmp DC. I dati sono stati campionati a 1000 Hz per 23 partecipanti e a 500 Hz per i restanti quattro partecipanti.
Analisi dei dati
L’elaborazione dei dati è stata effettuata utilizzando il toolbox EEGLAB(Delorme e Makeig, 2004) in MATLAB. Tutti i dati campionati a 1000 Hz sono stati ricampionati a 500 Hz. Un filtro passa alto è stato applicato a 0,6 Hz e i dati sono stati convertiti in riferimento medio.
Criteri di esclusione
Abbiamo definito due criteri per escludere i partecipanti dall’analisi. In primo luogo, abbiamo escluso i partecipanti che avevano una scarsa precisione di conteggio perché non possiamo essere sicuri che questi partecipanti fossero attenti durante l’intero compito. A questo scopo, abbiamo calcolato le correlazioni per ogni partecipante tra le sue risposte (numero di presentazioni di immagini contate in ogni prova) e il numero effettivo di cicli in cui l’immagine in questione è stata presentata. Abbiamo escluso cinque partecipanti il cui valore di correlazione r era inferiore a 0,9(Figura 6A).10.7554/eLife.22749.011Figure 6.Behavioral performance.(A) Istogramma tra tutti i partecipanti per l’accuratezza del conteggio misurata come correlazione tra la risposta del partecipante (numero di presentazioni di immagini contate in ogni prova) e il numero effettivo di presentazioni. Cinque partecipanti con una precisione di conteggio inferiore a r = 0,9 (linea tratteggiata rossa verticale) sono stati esclusi dall’analisi.(B) Trama di dispersione che mostra le risposte attraverso 56 prove per tutti i partecipanti inclusi nell’analisi. La dimensione di ogni punto corrisponde al numero di occorrenze in quel punto.(C) Un esempio di diagramma di dispersione per un singolo partecipante che dimostra il criterio di esclusione all’interno dei partecipanti per le singole prove. La linea continua (y=x) illustra la posizione teorica di risposte accurate. Per ogni prova, abbiamo calcolato la distanza tra la risposta del partecipante e il numero effettivo di cicli in cui è stata presentata la relativa immagine (cioè la distanza tra ogni punto del grafico e la linea continua). Il taglio all’interno del partecipante è stato poi definito come ±2,5 deviazioni standard dalla media di questa distanza. Le linee tratteggiate segnano il taglio all’interno del partecipante per l’esclusione di singole prove.DOI:http://dx.doi.org/10.7554/eLife.22749.011
Il secondo criterio si basava sulla qualità delle registrazioni EEG. I punti di campionamento erano considerati rumorosi se erano superiori a ±80 μV, se contenevano una fluttuazione improvvisa superiore a 40μV dal punto di campionamento precedente, o se il segnale era superiore a ±6 std dalla media dei dati di prova in ogni canale. I cicli in cui oltre il 2% dei punti di campionamento erano rumorosi sono stati considerati come cicli rumorosi. Per ogni canale, tutti i punti di campionamento all’interno dei cicli rumorosi sono stati sostituiti dal segnale medio durante la prova. I partecipanti per i quali più del 10% dei cicli erano rumorosi sono stati esclusi dall’analisi. Cinque ulteriori partecipanti sono stati esclusi in base a questo criterio per la scarsa registrazione EEG (in media, il 37% dei cicli era rumoroso per questi partecipanti). In totale sono stati inclusi nell’analisi 17 partecipanti rimanenti.
Inoltre, abbiamo escluso i sottoinsiemi di prove all’interno dei partecipanti. Per ogni partecipante abbiamo calcolato la media e la deviazione standard della differenza tra la risposta del partecipante (conteggio) e il numero di cicli in cui è stata presentata la relativa immagine. Abbiamo poi escluso tutte le prove in cui la risposta del partecipante è scesa oltre 2,5 deviazioni standard rispetto alla sua accuratezza media (ad esempio, Figura 6C). Da questo criterio, abbiamo escluso il 5,5% delle prove (52 su 952 prove in totale, 0-5 prove su 56 per ogni singolo partecipante).
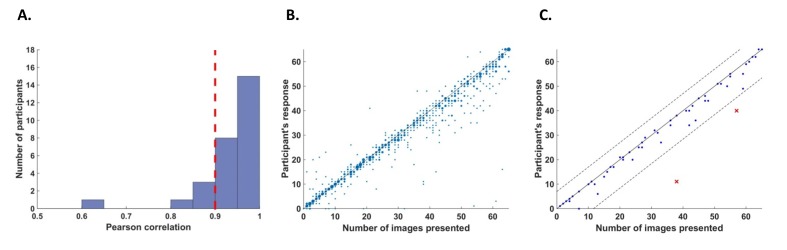
Figura 6.Performance comportamentale.(A) Istogramma di tutti i partecipanti per l’accuratezza del conteggio misurata come correlazione tra la risposta del partecipante (numero di presentazioni di immagini contate in ogni trial) e il numero effettivo di presentazioni. Cinque partecipanti con una precisione di conteggio inferiore a r = 0,9 (linea tratteggiata rossa verticale) sono stati esclusi dall’analisi.(B) Trama di dispersione che mostra le risposte attraverso 56 prove per tutti i partecipanti inclusi nell’analisi. La dimensione di ogni punto corrisponde al numero di occorrenze in quel punto.(C) Un esempio di diagramma di dispersione per un singolo partecipante che dimostra il criterio di esclusione all’interno dei partecipanti per le singole prove. La linea continua (y=x) illustra la posizione teorica di risposte accurate. Per ogni prova, abbiamo calcolato la distanza tra la risposta del partecipante e il numero effettivo di cicli in cui è stata presentata la relativa immagine (cioè la distanza tra ogni punto del grafico e la linea continua). Il taglio all’interno del partecipante è stato poi definito come ±2,5 deviazioni standard dalla media di questa distanza. Le linee tratteggiate segnano il taglio all’interno del partecipante per l’esclusione di singole prove.DOI:
http://dx.doi.org/10.7554/eLife.22749.011
Analisi spettrale
L’ampiezza del segnale EEG è stata estratta alle frequenze di etichettatura e intermodulazione applicando la trasformata veloce di Fourier (FFT) su ogni prova (50 s, 25.000 punti campione, risoluzione di frequenza = 0,02 Hz). I rapporti segnale/rumore (SNR) alla frequenza f sono stati calcolati dividendo l’ampiezza a f per l’ampiezza media su 20 frequenze vicine (da f-0.2Hz a f-0.02Hz e da f + 0.02 Hz a f + 0.2 Hz) (Srinivasan et al.,1999; Tononi e Edelman, 1998).
Componenti di intermodulazione
I componenti IM comprendono tutte le combinazioni lineari delle frequenze fondamentali che compongono il segnale di ingresso (n1f1 + n2f2, n = ±1,±2,±3…). Mentre nei nostri dati esiste un gran numero di potenziali componenti di IM, abbiamo focalizzato la nostra analisi sui quattro componenti di ordine più basso (f1-2f2 = 7.4 Hz, f1-f2 = 8,7 Hz, f1+f2 = 11,3 Hz e f1+2f2 = 12,6 Hz, dove f1 = 10 Hz e f2 = 1,3 Hz).
Analisi statistica
Per l’analisi degli effetti modulatori di certezza abbiamo utilizzato RStudio(RStudio Team, 2015) e lme4(Bates et al., 2015) per eseguire l’analisi lineare ad effetto misto dei dati. Sono state analizzate otto frequenze di interesse: f2 = 1,3 Hz e 2f2 = 2,6 Hz (SWIFT e armonica), f1 = 10 Hz e 2f1 = 20 Hz (SSVEP e armonica), e f1-2f2 = 7.4 Hz, f1-f2 = 8,7 Hz, f1+f2 = 11,3 Hz e f1+2f2 = 12,6 Hz (componenti IM). Abbiamo usato log2(ampiezza SNR) come variabile dipendente per tutte le analisi. Abbiamo scelto questa trasformazione perché l’ampiezza SNR ha un limite inferiore di 0 e non si distribuisce normalmente. La distribuzione di log2(SNR) invece è più vicina ad una distribuzione normale e permette una migliore omoscedasticità nei modelli lineari.
Per esaminare l’effetto modulatorio della certezza, abbiamo diviso le prove in 10 bins di certezza che vanno da 1 (certezza più bassa) a 10 (certezza più alta). I limiti del bin sono stati definiti in termini di percentuale di cicli in cui l’immagine più frequente è apparsa, creando così dei bin al 5% (le prove in cui l’immagine più frequente è apparsa nel 50-55%, 55-60%, … e 95-100% dei cicli sono definite rispettivamente come bin 1, 2, … e 10).
Sono stati applicati diversi modelli statistici per ciascuno dei tre livelli di analisi eseguiti: (1) all’interno di ciascuna delle 6 frequenze di interesse (ad es. f1, f2, f1+f2, ecc.), (2) all’interno della categoria IM (f1-2f2, f1-f2, f1+f2 e f1+2f2) e (3) tra le categorie di frequenza (SSVEP/SWIFT/IM). Tutte le analisi sono state eseguite su un ROI posteriore (30 elettrodi) compresi tutti gli elettrodi centro-parietali (CPz e CP1-CP6), temporo-parietali (TP7-TP10), parietali (Pz e P1-P8), parieto-occipitali (POz, PO3-PO4 e PO7-PO10) e occipitali (Oz,O1 e O2). I canali sono stati aggiunti a tutti i modelli come effetto casuale. Tutti gli effetti casuali sono stati ammessi sia per le intercettazioni casuali che per le pendenze.
Per esaminare se la certezza ha avuto un effetto modulatorio significativo all’interno di ogni frequenza di interesse, il primo livello di analisi ha incluso la certezza come effetto fisso, e il canale annidato all’interno dei partecipanti come effetto casuale. Per esaminare se c’era un effetto principale per la certezza all’interno di ogni categoria di frequenza (SSVEP/SWIFT/IM), il secondo livello di analisi includeva la certezza come effetto fisso, e la frequenza annidata all’interno del canale annidato nei partecipanti come effetto casuale. Per esaminare se l’effetto principale della certezza differisce tra le categorie di frequenza (cioè un’interazione significativa tra certezza e categoria di frequenza), il terzo livello di analisi ha incluso la certezza, la categoria di frequenza e un’interazione certezza-categoria come effetto fisso, e la frequenza annidata all’interno della categoria di frequenza annidata all’interno del canale annidato tra i partecipanti come effetto casuale.
Per verificare la significatività di un dato fattore o interazione, abbiamo eseguito test di likelihood ratio tra il modello completo, come descritto sopra, e il modello ridotto che non includeva il fattore o l’interazione in questione(Bates et al., 2015). Quando applicabile, abbiamo corretto i valori di p utilizzando il tasso di falsificazione(Yekutieli e Benjamini, 1999).
References
- Alink A, Schwiedrzik CM, Kohler A, Singer W, Muckli L. Stimulus predictability reduces responses in primary visual cortex. Journal of Neuroscience. 2010; 30:2960-2966. DOI | PubMed
- Auksztulewicz R, Friston K. Repetition suppression and its contextual determinants in predictive coding. Cortex. 2016; 80:125-140. DOI | PubMed
- Bastos AM, Vezoli J, Bosman CA, Schoffelen JM, Oostenveld R, Dowdall JR, De Weerd P, Kennedy H, Fries P. Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron. 2015; 85:390-401. DOI | PubMed
- Bates D, Mächler M, Bolker B, Walker S. Fitting linear Mixed-Effects models using lme4. Journal of Statistical Software. 2015; 67DOI
- Boremanse A, Norcia AM, Rossion B. An objective signature for visual binding of face parts in the human brain. Journal of Vision. 2013; 13DOI | PubMed
- Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007; 315:1860-1862. DOI | PubMed
- Chicherov V, Herzog MH. Targets but not flankers are suppressed in crowding as revealed by EEG frequency tagging. NeuroImage. 2015; 119:325-331. DOI | PubMed
- Clark A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences. 2013; 36:181-204. DOI | PubMed
- Clynes M. Unidirectional rate sensitivity: a biocybernetic law of reflex and humoral systems as physiologic channels of control and communication. Annals of the New York Academy of Sciences. 1961; 92:946-969. DOI | PubMed
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods. 2004; 134:9-21. DOI | PubMed
- Di Russo F, Pitzalis S, Aprile T, Spitoni G, Patria F, Stella A, Spinelli D, Hillyard SA. Spatiotemporal analysis of the cortical sources of the steady-state visual evoked potential. Human Brain Mapping. 2007; 28:323-334. DOI | PubMed
- Fahrenfort JJ, Snijders TM, Heinen K, van Gaal S, Scholte HS, Lamme VA. Neuronal integration in visual cortex elevates face category tuning to conscious face perception. PNAS. 2012; 109:21504-21509. DOI | PubMed
- Fontolan L, Morillon B, Liegeois-Chauvel C, Giraud AL. The contribution of frequency-specific activity to hierarchical information processing in the human auditory cortex. Nature Communications. 2014; 5DOI | PubMed
- Friston K. A theory of cortical responses. Philosophical Transactions of the Royal Society B: Biological Sciences. 2005; 360:815-836. DOI | PubMed
- Friston K. The free-energy principle: a rough guide to the brain?. Trends in Cognitive Sciences. 2009; 13:293-301. DOI | PubMed
- Friston KJ, Stephan KE. Free-energy and the brain. Synthese. 2007; 159:417-458. DOI | PubMed
- Geisler WS, Kersten D. Illusions, perception and Bayes. Nature Neuroscience. 2002; 5:508-510. DOI | PubMed
- Gundlach C, Müller MM. Perception of illusory contours forms intermodulation responses of steady state visual evoked potentials as a neural signature of spatial integration. Biological Psychology. 2013; 94:55-60. DOI | PubMed
- Henson RN. Neuroimaging studies of priming. Progress in Neurobiology. 2003; 70:53-81. DOI | PubMed
- Hohwy J. The Predictive Mind. Oxford University Press: Oxford, United Kingdom; 2013. DOI
- Hughes HC, Darcey TM, Barkan HI, Williamson PD, Roberts DW, Aslin CH. Responses of human auditory association cortex to the omission of an expected acoustic event. NeuroImage. 2001; 13:1073-1089. DOI | PubMed
- Hupé JM, James AC, Payne BR, Lomber SG, Girard P, Bullier J. Cortical feedback improves discrimination between figure and background by V1, V2 and V3 neurons. Nature. 1998; 394:784-787. DOI | PubMed
- Katyal S, Engel SA, He B, He S. Neurons that detect interocular conflict during binocular rivalry revealed with EEG. Journal of Vision. 2016; 16DOI | PubMed
- Kellermann T, Scholle R, Schneider F, Habel U. Decreasing predictability of visual motion enhances feed-forward processing in visual cortex when stimuli are behaviorally relevant. Brain Structure and Function. 2016;1-18. DOI | PubMed
- Kersten D, Mamassian P, Yuille A. Object perception as bayesian inference. Annual Review of Psychology. 2004; 55:271-304. DOI | PubMed
- Koenig-Robert R, VanRullen R, Tsuchiya N. Semantic Wavelet-Induced Frequency-Tagging (SWIFT) Periodically activates category selective areas while steadily activating early visual areas. PLoS One. 2015; 10DOI | PubMed
- Koenig-Robert R, VanRullen R. SWIFT: a novel method to track the neural correlates of recognition. NeuroImage. 2013; 81:273-282. DOI | PubMed
- Kok P, Brouwer GJ, van Gerven MA, de Lange FP. Prior expectations Bias sensory representations in visual cortex. Journal of Neuroscience. 2013; 33:16275-16284. DOI | PubMed
- Kok P, Jehee JF, de Lange FP. Less is more: expectation sharpens representations in the primary visual cortex. Neuron. 2012a; 75:265-270. DOI | PubMed
- Kok P, Lange PF. An Introduction to Model-Based Cognitive Neuroscience. Springer New York: New York, NY; 2015.
- Kok P, Rahnev D, Jehee JF, Lau HC, de Lange FP. Attention reverses the effect of prediction in silencing sensory signals. Cerebral Cortex. 2012b; 22:2197-2206. DOI | PubMed
- Kouh M, Poggio T. A canonical neural circuit for cortical nonlinear operations. Neural Computation. 2008; 20:1427-1451. DOI | PubMed
- Lee TS, Nguyen M. Dynamics of subjective contour formation in the early visual cortex. PNAS. 2001; 98:1907-1911. DOI | PubMed
- Mathys CD, Lomakina EI, Daunizeau J, Iglesias S, Brodersen KH, Friston KJ, Stephan KE. Uncertainty in perception and the hierarchical gaussian filter. Frontiers in Human Neuroscience. 2014; 8DOI | PubMed
- Mayer A, Schwiedrzik CM, Wibral M, Singer W, Melloni L. Expecting to see a letter: alpha oscillations as carriers of Top-Down sensory predictions. Cerebral Cortex. 2016; 26:3146-3160. DOI | PubMed
- Michalareas G, Vezoli J, van Pelt S, Schoffelen JM, Kennedy H, Fries P. Alpha-Beta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. Neuron. 2016; 89:384-397. DOI | PubMed
- Norcia AM, Appelbaum LG, Ales JM, Cottereau BR, Rossion B. The steady-state visual evoked potential in vision research: a review. Journal of Vision. 2015; 15DOI | PubMed
- Painter DR, Dux PE, Travis SL, Mattingley JB. Neural responses to target features outside a search array are enhanced during conjunction but not unique-feature search. Journal of Neuroscience. 2014; 34:3390-3401. DOI | PubMed
- Pascual-Leone A, Walsh V. Fast backprojections from the motion to the primary visual area necessary for visual awareness. Science. 2001; 292:510-512. DOI | PubMed
- Rao RP, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience. 1999; 2:79-87. DOI | PubMed
- Rauss K, Schwartz S, Pourtois G. Top-down effects on early visual processing in humans: a predictive coding framework. Neuroscience & Biobehavioral Reviews. 2011; 35:1237-1253. DOI | PubMed
- Regan D, Regan MP. Objective evidence for phase-independent spatial frequency analysis in the human visual pathway. Vision Research. 1988; 28:187-191. DOI | PubMed
- Ro T, Breitmeyer B, Burton P, Singhal NS, Lane D. Feedback contributions to visual awareness in human occipital cortex. Current Biology. 2003; 13:1038-1041. DOI | PubMed
- RStudio Team. RStudio: Integrated Development for R. Boston, MA; 2015.
- Sabra AI. The Optics of Ibn Al-Haytham: On Direct Vision. The Warburg Institute, University of London; 1989.
- Sedley W, Gander PE, Kumar S, Kovach CK, Oya H, Kawasaki H, Howard MA, Griffiths TD. Neural signatures of perceptual inference. eLife. 2016; 5DOI | PubMed
- Sherman MT, Kanai R, Seth AK, VanRullen R. Rhythmic influence of Top-Down perceptual priors in the phase of prestimulus occipital alpha oscillations. Journal of Cognitive Neuroscience. 2016; 28:1-13. DOI | PubMed
- Srinivasan MV, Laughlin SB, Dubs A. Predictive coding: a fresh view of inhibition in the retina. Proceedings of the Royal Society B: Biological Sciences. 1982; 216:427-459. DOI | PubMed
- Srinivasan R, Russell DP, Edelman GM, Tononi G. Increased synchronization of neuromagnetic responses during conscious perception. Journal of Neuroscience. 1999; 19:5435-5448. PubMed
- Summerfield C, Egner T. Expectation (and attention) in visual cognition. Trends in Cognitive Sciences. 2009; 13:403-409. DOI | PubMed
- Summerfield C, Trittschuh EH, Monti JM, Mesulam MM, Egner T. Neural repetition suppression reflects fulfilled perceptual expectations. Nature Neuroscience. 2008; 11:1004-1006. DOI | PubMed
- Todorovic A, de Lange FP. Repetition suppression and expectation suppression are dissociable in time in early auditory evoked fields. Journal of Neuroscience. 2012; 32:13389-13395. DOI | PubMed
- Todorovic A, van Ede F, Maris E, de Lange FP. Prior expectation mediates neural adaptation to repeated sounds in the auditory cortex: an MEG study. Journal of Neuroscience. 2011; 31:9118-9123. DOI | PubMed
- Tononi G, Edelman GM. Consciousness and complexity. Science. 1998; 282:1846-1851. DOI | PubMed
- van Kerkoerle T, Self MW, Dagnino B, Gariel-Mathis MA, Poort J, van der Togt C, Roelfsema PR. Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. Proceedings of the National Academy of Sciences. 2014; 111:14332-14341. DOI | PubMed
- Vetter P, Smith FW, Muckli L. Decoding sound and imagery content in early visual cortex. Current Biology. 2014; 24:1256-1262. DOI | PubMed
- Vialatte FB, Maurice M, Dauwels J, Cichocki A. Steady-state visually evoked potentials: focus on essential paradigms and future perspectives. Progress in Neurobiology. 2010; 90:418-438. DOI | PubMed
- Wacongne C, Labyt E, van Wassenhove V, Bekinschtein T, Naccache L, Dehaene S. Evidence for a hierarchy of predictions and prediction errors in human cortex. PNAS. 2011; 108:20754-20759. DOI | PubMed
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nature Neuroscience. 2002; 5:598-604. DOI | PubMed
- Yekutieli D, Benjamini Y. Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics. Journal of Statistical Planning and Inference. 1999; 82:171-196. DOI
- Zemon V, Ratliff F. Intermodulation components of the visual evoked potential: responses to lateral and superimposed stimuli. Biological Cybernetics. 1984; 50:401-408. DOI | PubMed
- Zhang P, Jamison K, Engel S, He B, He S. Binocular rivalry requires visual attention. Neuron. 2011; 71:362-369. DOI | PubMed
Fonte
Gordon N, Koenig-Robert R, Tsuchiya N, van Boxtel JJ, Hohwy J, et al. () Neural markers of predictive coding under perceptual uncertainty revealed with Hierarchical Frequency Tagging. eLife 6e22749. https://doi.org/10.7554/eLife.22749





