Abstract
Introduzione
Una riduzione locale della velocità in una folla di pedoni a piedi o nel traffico automobilistico urbano di solito porta alla formazione di regioni ad alta densità. Matematicamente parlando, una particella semovente, mossa da una camminata isotropa casuale con velocità dipendente dallo spazio, esplora lo spazio disponibile con una densità di probabilità inversamente proporzionale al valore locale della velocità(Schnitzer, 1993; Tailleur e Cates, 2009; Cates e Tailleur, 2015), trascorrendo un tempo più lungo nelle regioni lente che in quelle veloci. Di conseguenza, qualsiasi meccanismo che permetta di modulare sostanzialmente la velocità di propulsione locale può essere utilizzato come una strategia efficiente per il controllo della densità(Stenhammar et al., 2016). Nei batteri che nuotano, la proteorhodopsina (PR) fornisce un modo particolarmente conveniente per ottenere il controllo della velocità spaziale attraverso la proiezione di modelli di luce. PR è una pompa protonica azionata dalla luce che utilizza l’energia fotonica per pompare i protoni dal citoplasma, modulando così il corrispondente gradiente elettrochimico attraverso la membrana interna(Béjà et al., 2000). Poiché questa forza motrice protonica guida la rotazione del motore flagellare(Gabel e Berg, 2003), PR mette un ‘pannello solare’ su ogni cella permettendo di controllare a distanza la velocità di nuoto con la luce (Walteret al., 2007). Questo è stato recentemente sfruttato per controllare le velocità di rotazione delle micromacchine bio-ibride utilizzando i batteri come micropropulsori(Vizsnyiczai et al., 2017). Nei colloidi di Giano azionati dalla luce, i profili di velocità asimmetrici spazialmente possono anche influenzare l’orientamento delle particelle dando origine a un meccanismo di fototassi artificiale(Lozano et al., 2016). Arlt et al. (2018) hanno recentemente dimostrato che, proiettando un modello di illuminazione mascherato, i batteri “fotocinetici” (Wildee Mullineaux, 2017) possono essere accumulati in regioni oscure e impoveriti da quelli più luminosi formando così modelli binari. Qui dimostriamo che la densità batterica può essere controllata per formare modelli complessi riconfigurabili. Per fare questo sfruttiamo un proiettore Digital Light Processing (DLP) per modellare la luce con una risoluzione megapixel e con una gamma dinamica di 256 (8 bit) livelli di intensità luminosa. Indaghiamo sperimentalmente i limiti di validità della legge di proporzionalità inversa prevista tra densità locale e velocità. Dimostriamo che le deviazioni osservate da questa legge possono essere descritte quantitativamente da un modello teorico che tiene esplicitamente conto degli effetti di memoria nella risposta alla luce. Infine dimostriamo che un modello indipendente dal loop di controllo del feedback permette di modellare la densità con un’alta risoluzione spaziale e un’accuratezza del livello di grigio.
Risultati
La formazione della densità nei batteri fotocinetici o nei colloidi si basa sulla connessione tra densità e velocità locale. La densità ρ(𝐫)∝1/v(𝐫) è sempre una soluzione allo stato stazionario dell’equazione principale di una particella semovente con dinamica di riorientamento isotropa e velocità variabile spazialmente v(𝐫) (Cates e Tailleur, 2015). Nel nostro caso, v(𝐫)=v(I(𝐫)) dove 𝐫=(x,y) è la posizione nello spazio bidimensionale dell’immagine e I(𝐫) l’intensità della luce in 𝐫. Questo risultato presuppone che tutti i batteri abbiano la stessa risposta alla luce e che si adattino istantaneamente alle variazioni di intensità in modo che la velocità dipenda solo dal valore locale di I. Tuttavia, le sospensioni dei batteri che nuotano, sono note per essere caratterizzate da proprietà di motilità che si verificano in ampie distribuzioni e, in linea di principio, si potrebbe trovare un ampio spettro di risposte alla luce. Per quantificare l’effetto della luce sulle distribuzioni di velocità del nostro ceppo, abbiamo monitorato la dinamica batterica proiettando uno schema a scacchiera costituito da 12 diversi livelli di intensità luminosa. Per fare questo abbiamo accoppiato un proiettore DLP ad una configurazione personalizzata di video-microscopia che funziona sia in campo chiaro che in campo scuro (vedi Figura 1 e Materiali e metodi).
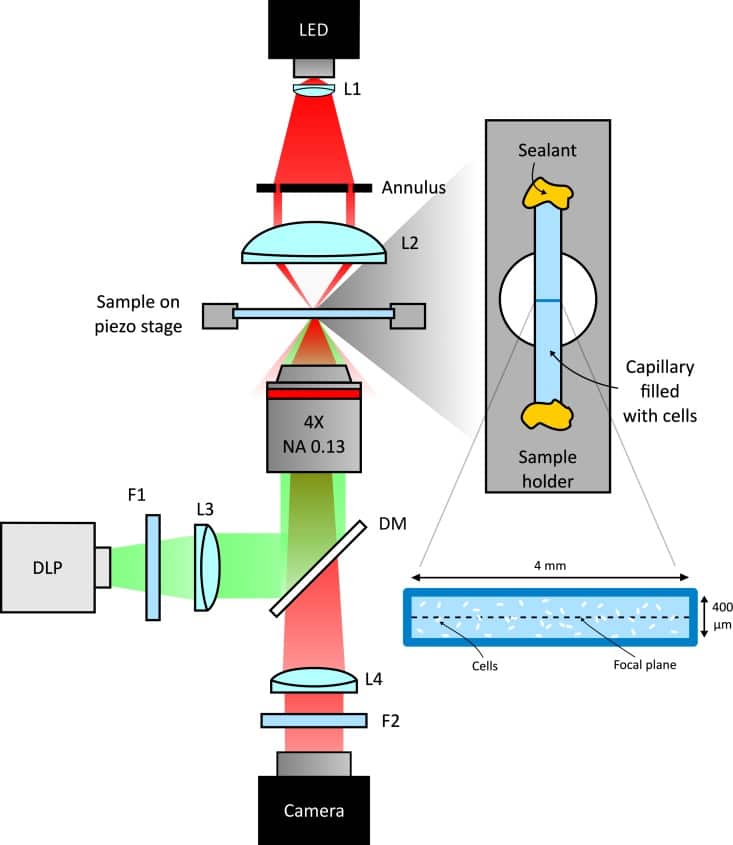
Figura 1.Schema del setup sperimentale.Rappresentazione schematica del microscopio invertito personalizzato utilizzato negli esperimenti (vedi Materiali e metodi). La luce verde di un proiettore DLP basato su DMD è filtrata da un filtro passa-banda F1 (lunghezza d’onda centrale 520 nm) e poi accoppiata all’obiettivo del microscopio attraverso uno specchio dicroico (DM). Un filtro passa-banda lungo (F2) impedisce alla luce di raggiungere la telecamera. I batteri sono sigillati in un microcapillare quadrato incollato su un portacampioni metallico con apertura circolare.
Utilizzando la microscopia dinamica differenziale (DDM)(Cerbino e Trappe, 2008; Wilson et al., 2011; Maggi et al., 2013) estraiamo i valori dipendenti dalla luce della v media e la deviazione standard σ delle distribuzioni di velocità (Figura 2(a))(vedi Materiali e metodi). Sebbene il valore assoluto della velocità di nuoto dipenda da diversi fattori (ceppo, terreno di crescita, ecc.), troviamo una risposta non lineare della velocità che è coerente con quanto precedentemente riportato per i batteri che esprimono PR. In particolare la curva della velocità rispetto all’intensità è molto ben adattata da un’iperbole che mostra la saturazione per grandi valori di intensità luminosa come già riportato in(Walter et al., 2007; Schwarz-Linek et al., 2016; Vizsnyiczai et al., 2017; Arlt et al., 2018).
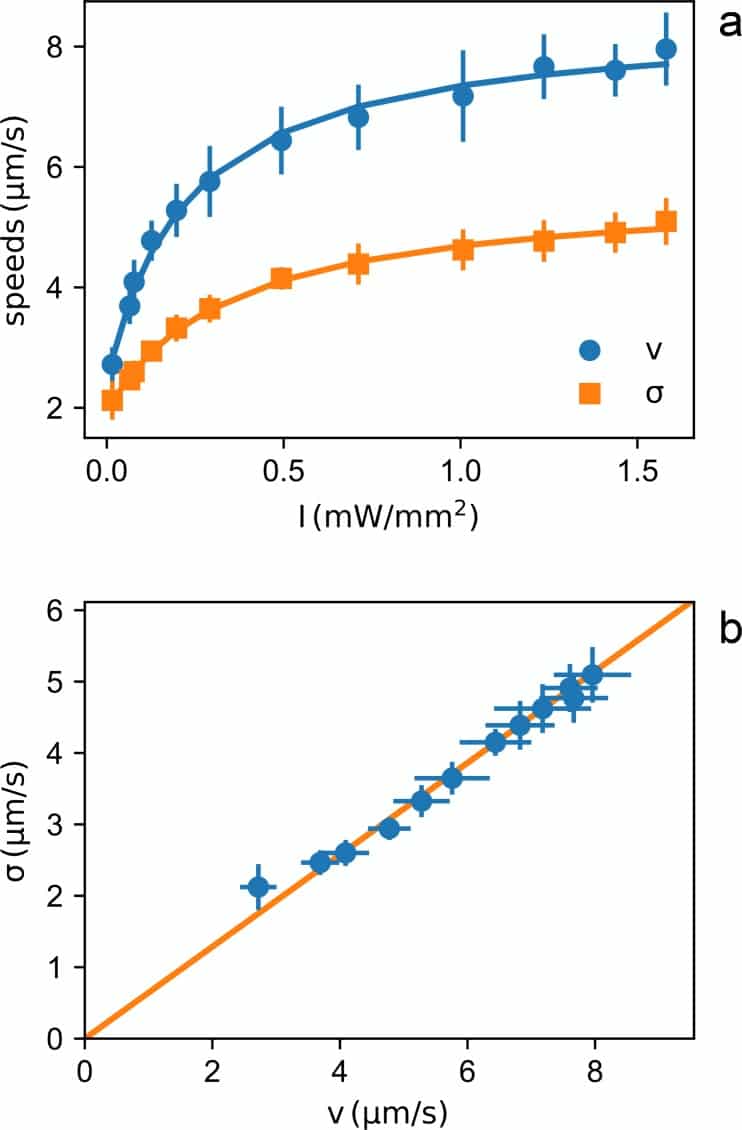
Figura 2 dati fonte 1.Dati di fonte per la Figura 2Dati di fonteper laFigura 2a) Valore medio v (cerchi) e deviazione standard σ (quadrati) della velocità batterica in funzione della densità di potenza della luce. I simboli e le barre di errore sono rispettivamente la media e la deviazione standard di 14 misurazioni ripetute di v e σ. Le curve si adattano alle iperboli.b) Tracciato parametrico di σ vsv. La linea è un adattamento lineare che passa attraverso lo zero.10.7554/eLife.36608.005Figure 2.Source data 1.Source data for Figure 2
Troviamo anche che, in tutto l’intervallo di intensità, v e σ sono direttamente proporzionali (vedi Figura 2(b)), suggerendo una legge di crescita omogenea per le singole velocità delle cellule vi(I)=visf(I), dove vis è la velocità di saturazione per la cella i-esima e f(I) è una funzione adimensionale che satura ad una per grandi intensità. È interessante notare che, in questo scenario, la velocità media v(I) sarà anche proporzionale a f(I) in modo che la densità di probabilità ρi per la generica cella i-esima sia proporzionale all’inverso della velocità media locale:ρi(𝐫)∝1vi(I(𝐫))∝1f(I(𝐫))∝1v(I(𝐫)).
Ciò implica che, nonostante le ampie distribuzioni di velocità, ci si aspetta che la densità locale sia determinata solo dalla velocità locale media, come impostata dal modello di intensità luminosa e misurata in DDM. Per convalidare questa ipotesi si utilizza un proiettore DLP per visualizzare un complesso schema di luce su uno strato di cellule dello spessore di 400 µm (Figura 1) che sono state preliminarmente esposte ad un’illuminazione uniforme e brillante per 5 minuti. Questo tempo è molto più lungo del tempo di risposta della velocità dei batteri (Figura 4), garantendo così che le cellule siano inizializzate per nuotare alla massima velocità. Il sistema di proiezione ha una risoluzione ottica di 2 µm che corrisponde approssimativamente alla dimensione di una singola cellula che rappresenta il ‘pixel’ fisico delle nostre immagini di densità. Questo valore fissa il limite per la risoluzione minima teorica delle configurazioni di densità che sarebbe raggiungibile se i batteri potessero essere disposti nello spazio in modo preciso e statico. In pratica, come vedremo, la risoluzione reale sarà sempre più grande per due motivi principali: (i) i batteri non rispondono istantaneamente alle leggere variazioni temporali, introducendo così una sfocatura nella mappa della velocità del bersaglio, (ii) lo stato stazionario è un insieme di schemi rumorosi che fluttuano costantemente a causa del nuoto e dei movimenti browniani dei batteri. Dopo aver proiettato un’immagine della Gioconda invertita, i batteri iniziano a concentrarsi nelle regioni buie mentre si allontanano dalle aree più illuminate. Dopo circa 4 minuti, la microscopia a campo scuro rivela una riconoscibile ‘replica’ batterica del dipinto di Leonardo, dove le aree più luminose corrispondono a regioni di cellule accumulate. Una volta raggiunto un modello stazionario, si raccoglie un’immagine media nel tempo da cui si estrae la densità batterica ρ* mostrata in Figura 3 normalizzata per essere uno quando uniforme (vedi Materiali e metodi).
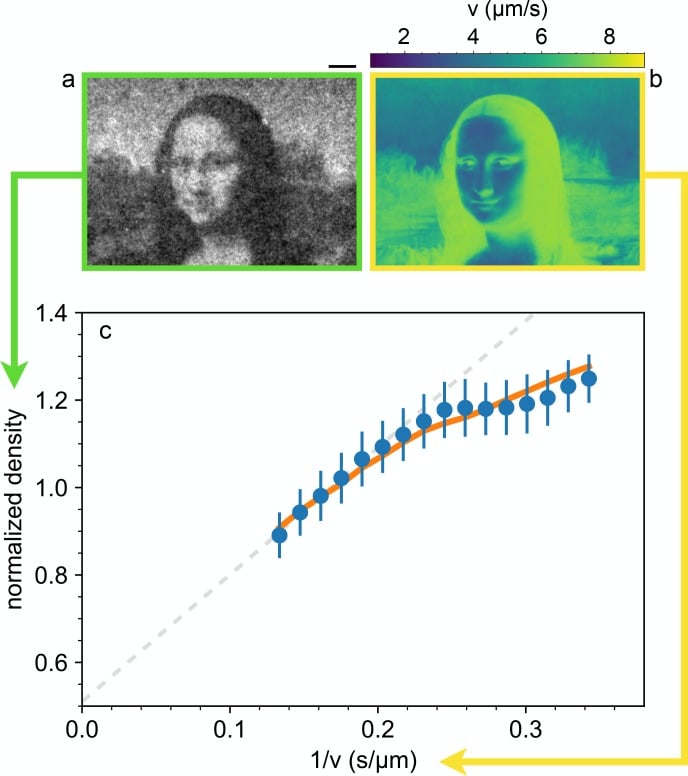
Figura 3 – Dati di origine 1.Densità di modellazione con la luce;dati di fonte per la Figura 3Dati di fonteper laFigura 3a) Immagine al microscopio in campo oscuro del campione ottenuta dopo aver proiettato uno schema di luce statica per 4 minuti (in media per 2 minuti). Barra di scala 100 µm.(b) Mappa della velocità locale ottenuta interpolando i punti di dati della Figura 2(a) ai valori dell’intensità della luce locale (proiettata).(c) I cerchi rappresentano il valore medio della densità del campione normalizzato su pixel dell’immagine corrispondente alla stessa intensità luminosa, tracciata in funzione della corrispondente velocità locale inversa. La linea tratteggiata è un adattamento lineare dei punti ad alta velocità. Le barre di errore sono la deviazione standard della densità allo stesso valore della velocità media inversa calcolata. La linea continua rappresenta la previsione dal modello di sfocatura della memoria descritto nel testo.10.7554/eLife.36608.007Figure 3-source data 1.Source data for Figure 3
Dividiamo l’immagine della densità in componenti corrispondenti allo stesso livello di illuminazione I. Facciamo quindi la media della densità all’interno di ciascun componente e riportiamo in Figura 3(c) il valore ottenuto in funzione della velocità media inversa 1/v(I) ottenuta dalla curva velocità vs intensità in Figura 2(a). Il lato ad alta velocità del grafico può essere molto ben adattato da una linea retta con un’intercetta finita q=0,5. Questo suggerisce che il 50% del totale degli oggetti a dispersione nel campo visivo risponde alla luce e può essere modulato spazialmente, mentre il restante 50% può essere attribuito a celle non mobili o insensibili alla luce e anche alla luce parassita generata lontano dal piano focale. Il rapporto tra la modulazione massima e minima della componente sensibile alla luce può essere ottenuto come max[ρ*-q]/min[ρ*-q]=2. Una forte deviazione dalla linearità è evidente nella regione ad alta densità/bassa velocità. Una violazione della legge ρ∝1/v può essere attribuita a molti fattori che non sono inclusi nella semplice teoria discussa sopra. In particolare, la teoria presuppone che la velocità sia una funzione locale dello spazio, cosa che si verificherebbe solo se i batteri si adattassero istantaneamente ai cambiamenti temporali dell’intensità della luce. Tuttavia, studi precedenti hanno dimostrato che la risposta della velocità non è istantanea, ma mostra un modello di rilassamento caratterizzato da molteplici intervalli temporali. Oltre ad un veloce tempo di rilassamento associato alla scarica della membrana(Walter et al., 2007), la sintasi ATP e la dinamica delle unità di statore dei motori flagellari introducono tempi più lenti nella dinamica di rilassamento della velocità(Tipping et al., 2013; Arlt et al., 2018). Utilizzando DDM abbiamo misurato la risposta della velocità ad un modello di luce uniforme la cui intensità passa tra due valori ogni 100 s. I risultati sono riportati nella Figura 4 e mostrano chiaramente la presenza di due tempi. La scala temporale breve è più piccola della nostra risoluzione temporale (1 s) e appare come un salto istantaneo che rappresenta circa una frazione β=0,44 del rilassamento totale. Segue un rilassamento più lento ed è ben dotato di una funzione esponenziale con una costante di tempo τm=35 s che è la stessa sia per il rilassamento ascendente che discendente. Come risultato, i batteri sperimenteranno una mappa di velocità efficace che è una versione sfocata di ciò che ci si aspetterebbe per una risposta istantanea V(𝐫)=v(I(𝐫)). Nel caso di celle di nuoto lisce, con una risposta alla luce in due fasi, calcoliamo che, per modulazioni di velocità deboli intorno ad un valore di base V0, la mappa della velocità effettiva può essere ottenuta come una semplice convoluzione (vedi Materiali e metodi):
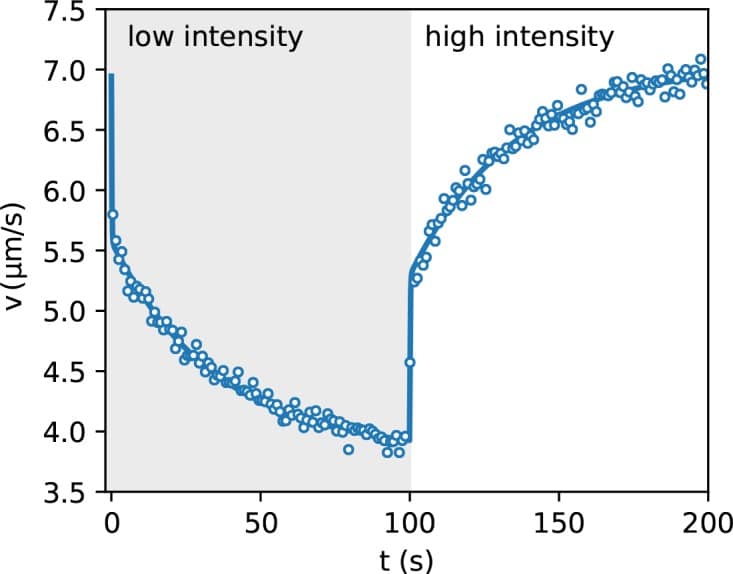
Figura 4 – Dati sorgente 1.Risposta di velocità alla luce passo passo.dati sorgente per la Figura 4Dati sorgenteper laFigura 4La velocità media dei batteri è in funzione del tempo durante l’illuminazione periodica con un’onda quadra del periodo 200 s. I cerchi aperti rappresentano i dati sperimentali mediamente su otto periodi, mentre la linea continua è una misura con una risposta a gradino seguita da un rilassamento esponenziale.10.7554/eLife.36608.009Cifra dati a 4 fonti 1.Dati fonte per la Figura 4
(1)w(x,y)≃βV(x,y)+(1-β)∫V(x-x′,y-y′)γ(x′,y′)𝑑x′𝑑y′ con γ(x,y) un kernel di convoluzione analitica nello spazio di Fourier:(2)γ~(q)=kqarctan(qk)dove q=qx2+qy2 è il modulo del vettore d’onda e k-1=v0τm. Supponendo che la distribuzione stazionaria rimanga isotropa anche in presenza di memoria, la relazione ρ∝1/w sarà allora ancora valida purché si utilizzi l’attuale, sfocata mappa di velocità w e non la mappa originale V corrispondente alla risposta istantanea. Possiamo quindi anticipare la densità stazionaria una volta calcolata la mappa della velocità reale w con la formula della convoluzione (1). Ricordando che solo una frazione α delle celle è mobile, la densità stazionaria normalizzata stimata sarà(3)ρ∗(x,y)=α(w(x,y)-1w-1¯-1)+1 dove w-1¯ è la media spaziale della velocità reale inversa w(x,y). Tracciando ρ* in funzione di 1/V troviamo che questo semplice modello spiega quantitativamente il comportamento della densità in Figura 3 con la scelta naturale dei parametri liberi α=0.5, β=0.44, e k-1=v¯τm=59 µm dove v¯ è la media spaziale di V(x,y). Questo risultato è certamente incoraggiante e stimola un’indagine più profonda e sistematica utilizzando schemi di luce più semplici. Il nostro obiettivo qui, tuttavia, è quello di indagare i limiti di risoluzione della modellazione della densità con batteri fotocinetici. Anche se gli effetti della memoria potrebbero essere ridotti eliminando i geni ATP-sintasi (Arltet al., 2018), con conseguente soppressione della componente lenta nel rilassamento della velocità, la risposta non sarà mai veramente istantanea. Oltre agli effetti della memoria, le interazioni steriche e/o idrodinamiche influenzeranno sempre la densità, ostacolando la penetrazione dei batteri e l’ulteriore accumulo in regioni densamente popolate. L’azione combinata di questi effetti sulla mappa della densità stazionaria non può essere facilmente incorporata in un modello teorico che fornisce precise previsioni quantitative con parametri a priori noti.
Una strategia alternativa e più pratica per migliorare l’accuratezza della formazione della densità, è quella di implementare un ciclo di controllo di feedback. Abbiamo impostato un loop di controllo automatico che esegue un’iterazione ogni 20 s, confrontando l’attuale mappa di densità con l’immagine di destinazione desiderata e aggiornando di conseguenza lo schema di illuminazione (vedere Materiali e metodi). I livelli di luce vengono aumentati in quelle regioni con una densità che supera il valore target e diminuiti dove la densità è inferiore. Ad ogni passo l’incremento dell’intensità della luce è semplicemente proporzionale alla differenza pixel per pixel delle immagini di destinazione e della densità effettiva. Quantifichiamo la distanza tra il modello di densità ottenuto e l’immagine target per la somma della differenza quadrata pixel per pixel dopo un’adeguata procedura di ridimensionamento (vedere Materiali e metodi).
Non appena il feedback viene attivato al tempo t0=6 min(Figura 5(a)) la distanza dal target inizia a diminuire raggiungendo un nuovo valore stazionario dopo circa 4 min. La mappa di densità stazionaria finale mostra un livello di dettaglio significativamente superiore all’immagine ottenuta prima dell’accensione del feedback(Figura 5(b,c)). L’immagine è stabile e la risoluzione non si deteriora per ore. Tuttavia una regione scura circonda l’area illuminata in modo che le cellule natatorie che escono dal campo visivo non tornino indietro e il numero di cellule mobili nell’area illuminata si riduce di circa il 50% in un’ora. Questo problema è il principale fattore limitante per la durata dei nostri modelli e potrebbe essere risolto in futuro utilizzando camere campione che corrispondono alle dimensioni dell’area illuminata. Come evidenziato nella Figura 5(d), il feedback precompensa questo effetto di sfocatura dovuto alla memoria convertendosi in una versione più nitida dell’immagine di destinazione iniziale. Risultati di qualità comparabile sono stati replicati quattro volte in ciascuna delle due repliche biologiche indipendenti.
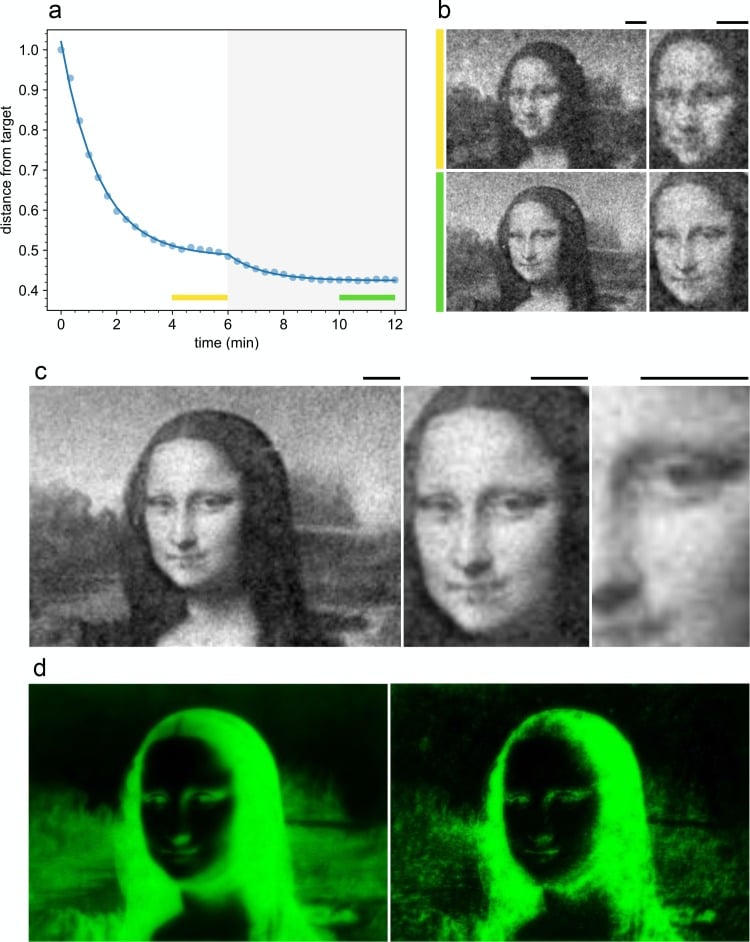
Figura 5 – Dati sorgente 1.2. Miglioramento del controllo della densità con un ciclo di feedback.dati sorgente per la Figura 5Dati sorgenteper laFigura 5(a) Evoluzione temporale della distanza dal bersaglio normalizzato al valore iniziale (cerchi) prima e dopo l’attivazione del ciclo di feedback (area grigia). Le barre gialle e verdi indicano l’intervallo di tempo su cui si fa la media delle mappe di densità (mostrate in (b)) prima e dopo il feedback rispettivamente. La curva completa è un fit con una doppia esponenziale.(b) Confronto della mappa di densità ottenuto facendo la media per 2 minuti prima (in alto) e dopo che il ciclo di feedback è stato attivato (in basso) (vedi barre colorate in(a))).c) Profilo di densità mediato nel tempo (6 min) con il feedback acceso.d) Modelli di intensità luminosa proiettata a t=0 (sinistra) e dopo l’ottimizzazione del feedback (destra). Le barre di scala sono 100 µm.10.7554/eLife.36608.011Figure 5-source data 1.Source data for Figure 5
Una caratteristica notevole di questo materiale a controllo ottico risiede nella sua intrinseca natura dinamica e riconfigurabile. A dimostrazione di questa proprietà mostriamo il morphing dinamico di uno strato batterico da un Albert Einstein ad un ritratto di Charles Darwin (vedi Figura 6 e Video 1) . Il morphing viene innescato passando istantaneamente tra le due immagini target sul proiettore DLP e converge esponenzialmente verso il secondo target in un tempo caratteristico di 1,8 min.
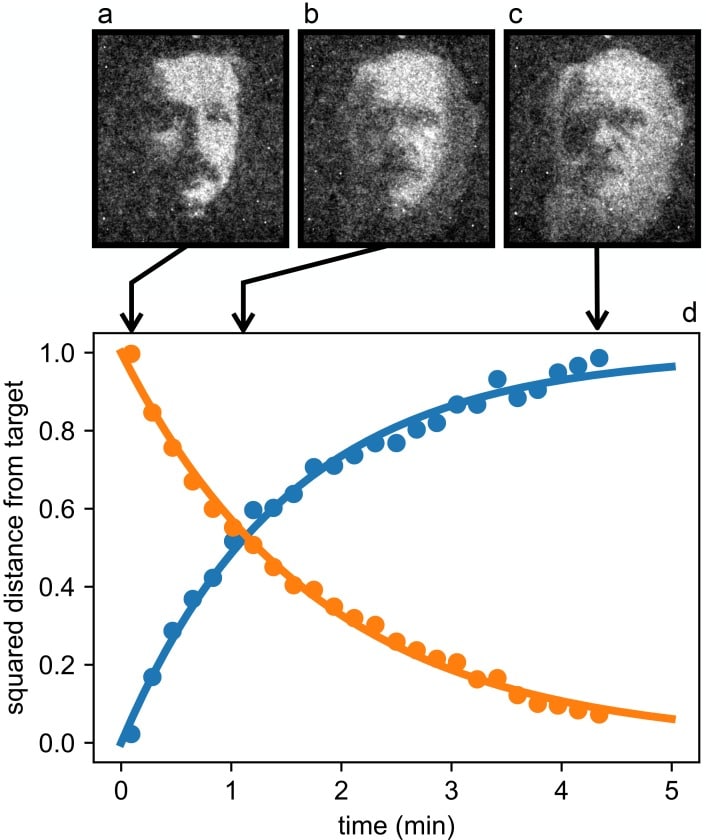
Figura 6 – Dati sorgente 1.Dati sorgente per la Figura 6Dati sorgenteper laFigura 6Partendo dalla modulazione di densità stazionaria(a) passiamo ad un nuovo modello di luce al tempo 0 e registriamo la distribuzione della densità dei batteri mentre si trasforma attraverso lo stato intermedio(b) e raggiunge lo stato finale(c).(d) Evoluzione nel tempo delle distanze quadrate normalizzate tra le mappe di densità istantanee e gli obiettivi iniziali (cerchi blu) e finali (cerchi arancioni). Le curve sono esponenziali.10.7554/eLife.36608.013Figure 6-source data 1.Source data for Figure 6

Video 1.Il video mostra il morphing dinamico di uno strato di batteri fotocinetici da un Albert Einstein a un ritratto di Charles Darwin (tempo totale 5 min).

Figura 1.Schema dell’allestimento sperimentale.Rappresentazione schematica del microscopio invertito personalizzato utilizzato negli esperimenti (vedi Materiali e metodi). La luce verde di un proiettore DLP basato su DMD è filtrata da un filtro passa-banda F1 (lunghezza d’onda centrale 520 nm) e poi accoppiata all’obiettivo del microscopio attraverso uno specchio dicroico (DM). Un filtro passa-banda lungo (F2) impedisce alla luce di raggiungere la telecamera. I batteri sono sigillati in un microcapillare quadrato incollato su un portacampioni metallico con apertura circolare.

Figura 2 dati fonte 1.Dati della fonte per la Figura 2Dati della fonteper laFigura 2a) Valore medio v (cerchi) e deviazione standard σ (quadrati) della velocità batterica in funzione della densità di potenza della luce. I simboli e le barre di errore sono rispettivamente la media e la deviazione standard di 14 misurazioni ripetute di v e σ. Le curve si adattano alle iperboli.b) Tracciato parametrico di σ vsv. La linea è un adattamento lineare che passa attraverso lo zero.10.7554/eLife.36608.005Figure 2.Source data 1.Source data for Figure 2

Figura 3 – Dati sorgente 1.Densità di modellazione con la luce;dati di fonte per la Figura 3Dati di fonteper laFigura 3a) Immagine al microscopio in campo oscuro del campione ottenuta dopo aver proiettato uno schema di luce statica per 4 minuti (in media per 2 minuti). Barra di scala 100 µm.(b) Mappa della velocità locale ottenuta interpolando i punti di dati della Figura 2(a) ai valori dell’intensità della luce locale (proiettata).(c) I cerchi rappresentano il valore medio della densità del campione normalizzato su pixel dell’immagine corrispondente alla stessa intensità luminosa, tracciata in funzione della corrispondente velocità locale inversa. La linea tratteggiata è un adattamento lineare dei punti ad alta velocità. Le barre di errore sono la deviazione standard della densità allo stesso valore della velocità media inversa calcolata. La linea continua rappresenta la previsione dal modello di sfocatura della memoria descritto nel testo.10.7554/eLife.36608.007Figure 3-source data 1.Source data for Figure 3

Figura 4 dati fonte 1.Risposta rapida al passaggio della luce.dati sorgente per la Figura 4Dati sorgenteper laFigura 4La velocità media dei batteri è in funzione del tempo durante l’illuminazione periodica con un’onda quadra del periodo 200 s. I cerchi aperti rappresentano i dati sperimentali mediamente su otto periodi, mentre la linea continua è una misura con una risposta a gradino seguita da un rilassamento esponenziale.10.7554/eLife.36608.009Cifra dati a 4 fonti 1.Dati fonte per la Figura 4

Figura 5 – Dati sorgente 1.2. Miglioramento del controllo della densità con un ciclo di feedback.dati fonte per la Figura 5Dati fonteper laFigura 5(a) Evoluzione temporale della distanza dal bersaglio normalizzato al valore iniziale (cerchi) prima e dopo l’attivazione del ciclo di feedback (area grigia). Le barre gialle e verdi indicano l’intervallo di tempo su cui si fa la media delle mappe di densità (mostrate in (b)) prima e dopo il feedback rispettivamente. La curva completa è un fit con una doppia esponenziale.(b) Confronto della mappa di densità ottenuto facendo la media per 2 minuti prima (in alto) e dopo che il ciclo di feedback è stato attivato (in basso) (vedi barre colorate in(a))).c) Profilo di densità mediato nel tempo (6 min) con il feedback acceso.d) Modelli di intensità luminosa proiettata a t=0 (sinistra) e dopo l’ottimizzazione del feedback (destra). Le barre di scala sono 100 µm.10.7554/eLife.36608.011Figure 5-source data 1.Source data for Figure 5

Figura 6 – Dati sorgente 1.Dati sorgente per la Figura 6Dati sorgenteper laFigura 6Partendo dalla modulazione di densità stazionaria(a) passiamo ad un nuovo modello di luce al tempo 0 e registriamo la distribuzione della densità dei batteri mentre si trasforma attraverso lo stato intermedio(b) e raggiunge lo stato finale(c).(d) Evoluzione nel tempo delle distanze quadrate normalizzate tra le mappe di densità istantanee e gli obiettivi iniziali (cerchi blu) e finali (cerchi arancioni). Le curve sono esponenziali.10.7554/eLife.36608.013Figure 6-source data 1.Source data for Figure 6

Video 1.Il video mostra il morphing dinamico di uno strato di batteri fotocinetici da un Albert Einstein a un ritratto di Charles Darwin (tempo totale 5 min).
Discussione
Sebbene le modulazioni di densità indotte dalla luce possano essere ottenute in grandi campioni di sistemi colloidali (passivi) browniani, i materiali attivi forniscono una prestazione ampiamente superiore sia in termini di potenza richiesta che di tempo di risposta. La distribuzione stazionaria della densità dei colloidi browniani è regolata dalla legge di Boltzmann che stabilisce che il rapporto logaritmico tra la densità massima e minima è dato da log(ρmaxρmin)=-ΔUkBT, dove ΔU è la differenza di energia ottica tra le regioni più luminose e quelle più scure. Per una perlina di plastica o di vetro di raggio a=1µm in acqua, questa differenza di energia può essere stimata nel regime di Rayleigh come (Ashkinet al., 1986) ΔU≈a3I/c dove I è la massima densità di potenza e c è la velocità della luce. Per un livello di contrasto paragonabile a quelli indicati sopra, log(ρmax/ρmin)≈1, la densità di potenza richiesta sarebbe I≈kBTc/a3≈1 W/mm2. Questo valore è di tre ordini di grandezza superiore alle densità di potenza massime utilizzate nei nostri esperimenti. Il nostro sistema attivo è anche molto più veloce del suo controstampo browniano, come evidenziato dal confronto dei tempi di formazione del modello. Sia nel caso attivo che passivo, la dinamica è governata dall’interazione tra diffusione e deriva con le caratteristiche temporali τdiff e τdrift. Chiamando ℓ=1 mm la scala di lunghezza più grande nel modello di destinazione, si ottiene per il caso attivo τdrift≈ℓ/v≈200 s dove abbiamo usato v=5 µm/s come velocità tipica di nuoto. Una scala di tempo di diffusione può essere ottenuta come τdiff≈ℓ2/2D dove D è il coefficiente attivo di diffusione traslazionale. Per i batteri di tipo selvaggio, che si muovono con una dinamica di corsa e di caduta, D=v2τrun dove τrun≈1 s è la durata media di una corsa. Il tempo di diffusione caratteristico corrispondente è τdiff≈ℓ2/2D≈2×104 s. Questo tempo può essere notevolmente ridotto se, come nel nostro caso, si sopprime il rotolamento e si utilizza un ceppo di nuoto liscio con un tempo di riorientamento molto maggiore τrot≈20 s (Berg, 1993). In questo caso il tempo di diffusione scende a τdiff≈103 s, portando ad un più rapido rilassamento verso lo stato stazionario. Nel caso di Brownian la scala dei tempi di deriva è data da τdrift≈μkBT/ℓ≈106 s dove μ=50 µm/s pN è la mobilità di una microsfera con raggio di 1 µm. La stessa particella colloidale ha una diffusività D=μkBT=0,2 µm2/s dando di nuovo τdiff≈ℓ2/2D≈ℓ2/2D≈106 s. Riassumendo, l’utilizzo di forze ottiche per ottenere una modulazione di densità comparabile per le particelle browniane richiederebbe potenze mille volte maggiori e da 103 a 104 volte più lunghe.
In conclusione, abbiamo dimostrato che una sospensione di batteri natatori, con velocità otticamente controllabile, può fornire una nuova classe di materiali attivi controllabili dalla luce la cui densità può essere accuratamente, reversibilmente e rapidamente modellata utilizzando un proiettore di luce a bassa potenza. Una strategia alternativa per produrre modelli statici di batteri è la ‘biofilm lithography’, dove un modello ottico di luce blu viene utilizzato per indurre l’espressione delle proteine di membrana che promuovono l’attaccamento cellula-cellula e cellula-substrato (Jin eRiedel-Kruse, 2018). A differenza della nostra modellazione della densità basata sulla motilità, questi modelli sono statici e si formano su una scala temporale di diverse ore. È interessante notare che le due tecniche potrebbero essere utilizzate in combinazione per ottenere una litografia biofilm più veloce e complessa (ad esempio tridimensionale) fissando con luce blu un modello di modello ottenuto dalla modulazione di velocità con luce verde. Con un’ulteriore ingegneria genetica, i batteri potrebbero essere eventualmente incapsulati in gusci di silicato(Müller et al., 2008) producendo solide strutture permanenti per applicazioni di micromeccanica o microottica. Infine, la possibilità di controllo spaziale e temporale della densità dei batteri mobili potrebbe anche portare a nuove strategie per il trasporto e la manipolazione di piccoli carichi all’interno di microdispositivi Maggi et al. (2018).
Materiali e metodi
Produzione di cellule fotocinetiche
Per tutti gli esperimenti abbiamo usato il ceppo di E. coli HCB437(Wolfe et al., 1987) trasformato con un plasmide che codifica il PR sotto il controllo del promotore araC-pBAD (Biobricks, BBa_K1604010 inserito nella spina dorsale plasmidica pSB1C3). Le colonie di E. coli provenienti da stock congelati vengono coltivate durante la notte sul sito 33∘C su piastre di agar LB integrate con kanamicina (Kan 30 µg/mL) e cloramfenicolo (Cam 20 µg/mL). Una singola colonia viene raccolta e coltivata staticamente durante la notte su 33∘C in 10 mL di brodo M9 (sali M9 con 0,2% di glucosio, 0,2% di casaminoacidi) integrato con antibiotici come prima. La coltura durante la notte viene diluita 100 volte in 5 mL del terreno precedente, coltivato a 33∘C, 200 rpm. 5 mM di arabinosio e 20 µM di retina vengono aggiunti una volta OD590≈ 0,2, mantenendo la coltura al buio per evitare la degradazione della retina. Una volta OD590 ≈ 0,8, le cellule sono raccolte per centrifugazione (1500 rcf, 5′). Il pellet risultante viene lavato due volte per centrifugazione (1500 rcf, 5′) con tampone di motilità (MB: 0,1 mM EDTA, 10 mM tampone fosfato e 0,2% Tween20). La sospensione batterica viene infine regolata ad un OD di lavoro ± 590 2,0.
Preparazione del campione
100 µL della sospensione batterica preparata vengono iniettati in un capillare di vetro (CM Scientific – Rect. boro capillari 0,40 × 4 mm), sigillato su entrambi i lati con grasso sotto vuoto (Sigma-Aldrich). Il capillare viene poi posto sotto il microscopio ottico e osservato in campo luminoso e scuro illuminazione messa a fuoco sul piano al centro del capillare.
Ottica
L’imaging in campo chiaro e in campo scuro sono stati eseguiti utilizzando un microscopio ottico personalizzato invertito dotato di un obiettivo di ingrandimento 4 × (Nikon; NA = 0,13) e una fotocamera CMOS ad alta sensibilità (Hamamatsu Orca-Flash 2,8) (vedi Figura 1). La modellazione della luce è stata eseguita utilizzando un proiettore per l’elaborazione digitale della luce (DLP) (Texas Instruments DLP Lightcrafter 4500) accoppiato allo stesso obiettivo per microscopio utilizzato per l’imaging. La dimensione di un pixel del proiettore DLP (al quadrato) riprodotto sul piano del campione risulta essere di 2 µm. Tutte le immagini in campo scuro sono state divise per l’immagine in campo piano ottenuta applicando un filtro gaussiano sulla rispettiva sospensione batterica omogenea (sotto un’illuminazione verde uniforme) come descritto di seguito. La sottrazione di fondo piatto (quinto percentile dell’istogramma dell’immagine) è stata applicata solo ai fotogrammi che appaiono nella Figura 6.
Microscopia dinamica differenziale (DDM)
Per eseguire il DDM calcoliamo la quantità:(4)g(𝐪,t′,t)=⟨|M(𝐪,t′)-M(𝐪,t′+t)|2⟩where M(𝐪,t) è la trasformata spaziale di Fourier al vettore d’onda 𝐪 dell’immagine del campo luminoso catturata al momento t. Assumendo l’invarianza temporale e l’isotropia nel movimento batterico g(𝐪,t′,t) dipende solo dal tempo t nell’equazione (4) e dal modulo del vettore d’onda q=|𝐪|, cioè g(𝐪,t,t′)=g(q,t). Il g(q,t) è collegato alla funzione di dispersione intermedia (ISF) F(q,t):(5)g(q,t)=A(q)F(q,t)+B(q)dove A(q) e B(q) sono fattori dipendenti dal tempo e correlati, rispettivamente, al numero e alla forma dei batteri e al rumore di fondo delle immagini. Seguendo Wilson et al., 2011 usiamo il modello ISF per le cellule lisce indipendenti:(6)F(q,t)=(1-α)e-q2Dt+αe-q2Dt∫0∞𝑑v′P(v′)sinc(qv′t)dove α è la frazione di cellule mobili, D il coefficiente di diffusione browniana e P(v′) la distribuzione di Schultz:(7)P(v′)=1v′(Z+1vv′)Z+1exp(-Z+1vv′)Γ(Z+1)
Qui v è la velocità media, Γ è la funzione gamma di Eulero e Z è correlata alla deviazione standard della velocità σ con la formula Z=(v/σ)2-1. I parametri rilevanti discussi nel testo principale v e σ sono estratti inserendo la g(q,t) sperimentale nella q-range 0,45 μm-1<q<1,2 μm-1 con le equazioni 5, 6 e 7.
Analisi dell’immagine
Si presume che le immagini in campo scuro siano proporzionali alla densità batterica modulata da un involucro che varia lentamente a causa delle disomogeneità dell’illuminazione. Questa correzione del campo piatto ρ0(𝐫) si ottiene acquisendo 100 fotogrammi a 25 fps all’inizio degli esperimenti quando la densità batterica è omogenea. Questi frame sono mediati e poi filtrati con un kernel gaussiano con una grande deviazione standard (≈100µm). La densità sperimentale normalizzata ρ∗(𝐫) si ottiene calcolando prima un campo di densità grezzo ρ(𝐫) (media di 50 fotogrammi a 25 fps) e poi dividendo per ρ0, cioè ρ∗(𝐫)=ρ(𝐫)/ρ0(𝐫).
Per il calcolo della distanza tra ρ∗(𝐫) e la densità di destinazione ρtar(𝐫) calcoliamo prima la scala ρ∗(𝐫) in modo che il decimo e il novantesimo percentile dei due istogrammi delle immagini coincidano:ρs(𝐫)=ρ90%tar-ρ10%tarρ90%∗-ρ10%∗(ρ∗(𝐫)-ρ10%∗)+ρ10%tar.
La distanza 𝖽𝗂𝗌𝗍 viene quindi calcolata come:𝖽𝗂𝗌𝗍=[∑𝐫[ρs(𝐫)-ρtar(𝐫)]2]12 dove la somma corre sui pixel dell’immagine 𝐫.
Modellazione degli effetti della memoria in risposta alla velocità
Una cella di nuoto liscia con una risposta in due fasi all’intensità della luce e che viaggia in direzione x su un profilo di velocità imposto dalla luce V(x), avrà una velocità effettiva al tempo t dato da:(8)v(t)=βV(x(t))+(1-β)∫0∞V(x(t-t′))e-t′/τm𝑑t′ dove x(t) è la posizione della cella al momento t. Per un profilo di velocità debolmente variabile V(x)=V0+δV(x) possiamo trasformare la suddetta convoluzione temporale in una convoluzione spaziale assumendo x(t)≈x(0)+V0t:(9)v(x)≃βV(x)+(1-β)k2∫-∞∞V(x-s)e-k|s|𝑑swhere abbiamo anche ipotizzato che un numero uguale di batteri viaggerà nella direzione opposta. Ipotizzando l’isotropia e utilizzando il fatto che, nel limite di modulazione debole, la densità è omogenea all’ordine zero, possiamo facilmente generalizzare al caso tridimensionale e scrivere:(10)v(𝐫)≃βV(𝐫)+(1-β)k4π∫V(𝐫-su^)e-k|s|𝑑s𝑑Ω=βV(𝐫)+(1-β)∫V(𝐫-𝐫′)Γ(𝐫′)d3r′dove Γ(𝐫)=(k/4πr2)e-kr è un kernel di convoluzione 3D. Il nostro sistema di proiezione della luce è tale che i modelli di luce non variano in modo significativo su tutta la profondità del campione in modo da poter assumere V(x,y,z)=V(x,y) ed esprimere la distribuzione effettiva della velocità come una convoluzione 2D(11)v(x,y)≃βV(x,y)+(1-β)∫V(x-x′,y-y′)γ(x′,y′)𝑑x′𝑑y′con γ(x,y)=∫-∞∞∞Γ(x,y,z)𝑑z. Sebbene il kernel di convoluzione γ non sia analitico nello spazio reale, la sua trasformata di Fourier è analitica rendendo le convoluzioni facili da calcolare numericamente:(12)γ~(q)=kqarctan(qk)dove q=qx2+qy2.
Feedback
Il (n+1)-esimo schema di illuminazione del pixel 𝐫 è aggiornato come segue:In+1(𝐫)=In(𝐫)+PΔρ(𝐫),dove P>0 è un parametro di controllo proporzionale e Δρ è la differenza tra la densità scalare e la densità target:Δρ(𝐫)=ρs(𝐫)-ρtar(𝐫)
Se, ad esempio, la densità in scala è più grande del target su 𝐫, la densità di potenza proiettata a quel pixel sarà aumentata. Ciò aumenterà la velocità dei batteri e di conseguenza ridurrà la loro densità locale.
References
- Arlt J, Martinez VA, Dawson A, Pilizota T, Poon WCK. Painting with light-powered bacteria. Nature Communications. 2018; 9DOI | PubMed
- Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Optics Letters. 1986; 11:288-290. DOI | PubMed
- Berg HC. Random Walks in Biology. Princeton University Press; 1993.
- Béjà O, Aravind L, Koonin EV, Suzuki MT, Hadd A, Nguyen LP, Jovanovich SB, Gates CM, Feldman RA, Spudich JL, Spudich EN, DeLong EF. Bacterial rhodopsin: evidence for a new type of phototrophy in the sea. Science. 2000; 289:1902-1906. DOI | PubMed
- Cates ME, Tailleur J. Motility-Induced phase separation. Annual Review of Condensed Matter Physics. 2015; 6:219-244. DOI
- Cerbino R, Trappe V. Differential dynamic microscopy: probing wave vector dependent dynamics with a microscope. Physical Review Letters. 2008; 100DOI | PubMed
- Gabel CV, Berg HC. The speed of the flagellar rotary motor of Escherichia coli varies linearly with protonmotive force. PNAS. 2003; 100:8748-8751. DOI | PubMed
- Jin X, Riedel-Kruse IH. Biofilm lithography enables high-resolution cell patterning via optogenetic adhesin expression. PNAS. 2018; 115:3698-3703. DOI | PubMed
- Lozano C, Ten Hagen B, Löwen H, Bechinger C. Phototaxis of synthetic microswimmers in optical landscapes. Nature Communications. 2016; 7DOI | PubMed
- Maggi C, Angelani L, Frangipane G, Di Leonardo R. Currents and flux-inversion in photokinetic active particles. Soft Matter. 2018; 14:4958-4962. DOI | PubMed
- Maggi C, Lepore A, Solari J, Rizzo A, Di Leonardo R. Motility fractionation of bacteria by centrifugation. Soft Matter. 2013; 9:10885-10890. DOI
- Müller WE, Engel S, Wang X, Wolf SE, Tremel W, Thakur NL, Krasko A, Divekar M, Schröder HC. Bioencapsulation of living bacteria (Escherichia coli) with poly(silicate) after transformation with silicatein-alpha gene. Biomaterials. 2008; 29:771-779. DOI | PubMed
- Schnitzer MJ. Theory of continuum random walks and application to chemotaxis. Physical Review E. 1993; 48:2553-2568. DOI | PubMed
- Schwarz-Linek J, Arlt J, Jepson A, Dawson A, Vissers T, Miroli D, Pilizota T, Martinez VA, Poon WCK. Escherichia coli as a model active colloid: A practical introduction. Colloids and Surfaces B: Biointerfaces. 2016; 137:2-16. DOI | PubMed
- Stenhammar J, Wittkowski R, Marenduzzo D, Cates ME. Light-induced self-assembly of active rectification devices. Science Advances. 2016; 2DOI | PubMed
- Tailleur J, Cates ME. Sedimentation, trapping, and rectification of dilute Bacteria. Epl. 2009; 86DOI
- Tipping MJ, Steel BC, Delalez NJ, Berry RM, Armitage JP. Quantification of flagellar motor stator dynamics through in vivo proton-motive force control. Molecular Microbiology. 2013; 87:338-347. DOI | PubMed
- Vizsnyiczai G, Frangipane G, Maggi C, Saglimbeni F, Bianchi S, Di Leonardo R. Light controlled 3D micromotors powered by Bacteria. Nature Communications. 2017; 8DOI | PubMed
- Walter JM, Greenfield D, Bustamante C, Liphardt J. Light-powering Escherichia coli with proteorhodopsin. PNAS. 2007; 104:2408-2412. DOI | PubMed
- Wilde A, Mullineaux CW. Light-controlled motility in prokaryotes and the problem of directional light perception. FEMS Microbiology Reviews. 2017; 41:900-922. DOI | PubMed
- Wilson LG, Martinez VA, Schwarz-Linek J, Tailleur J, Bryant G, Pusey PN, Poon WC. Differential dynamic microscopy of bacterial motility. Physical Review Letters. 2011; 106DOI | PubMed
- Wolfe AJ, Conley MP, Kramer TJ, Berg HC. Reconstitution of signaling in bacterial chemotaxis. Journal of Bacteriology. 1987; 169:1878-1885. DOI | PubMed
Fonte
Frangipane G, Dell’Arciprete D, Petracchini S, Maggi C, Saglimbeni F, et al. () Dynamic density shaping of photokinetic . eLife 7e36608. https://doi.org/10.7554/eLife.36608





