Abstract
Introduzione
La maggior parte degli strumenti optogenetici si basa su una proteina fotorecettore con un dominio di rilevamento della luce che regola un dominio effettoriale, che a sua volta genera un segnale biologico come l’espressione genica. Si può considerare un modello semplificato in cui un fotorecettore viene prodotto in uno stato “a terra” e commutato in uno stato “attivo” attivando le lunghezze d’onda (cioè la fotoconversione in avanti) (Butler et al, 1964). I fotorecettori a stato attivo ritornano termicamente allo stato di terra con una caratteristica scala temporale che va dai millisecondi (Jaubert et al, 2007) a più di un mese (Rockwell et al, 2012). Alcuni fotorecettori, esemplificati dalle famiglie del fitocromo lineare tetrapirrolo (bilin)-legante (Phy) e del cianobatteriocromo (CBCR), sono anch’essi fotorevertibili quando la reversione dallo stato attivo a quello di terra è guidata dalla disattivazione delle lunghezze d’onda (Rockwell et al, 2006; Möglich et al, 2010; Rockwell & Lagarias, 2010).
I sistemi a due componenti (TCS) sono percorsi di trasduzione del segnale che controllano l’espressione genica e altri processi in risposta a stimoli chimici o fisici (input). I TCS canonici comprendono due proteine: un sensore istidina chinasi (SK) e un regolatore di risposta (RR). L’SK è prodotto in uno stato di terra, che spesso (ma non sempre) ha una bassa attività chinasi verso l’RR. Quando rileva un ingresso attraverso un dominio di rilevamento N-terminale, lo SK utilizza l’ATP per autofosforilare un residuo di istidina all’interno di un dominio C-terminale chinasi. Questo gruppo fosforilico viene poi trasferito ad un aspartato sul RR. Nella maggior parte dei casi, il fosforilato RR (RR~P) si lega ad un promotore di destinazione, attivando la trascrizione. Molti SK sono bifunzionali e il dominio chinasi dephosphorilato del dominio RR~P in assenza dell’ingresso o della presenza di un ingresso diverso e disattivante.
In precedenza abbiamo ingegnerizzato due TCS fotoriproducibili Escherichia coli spettralmente distinti, CcaSR e Cph8-OmpR (Fig EV1 eDataset EV1) (Levskaya et al, 2005; Tabor et al, 2011; Schmidl et al , 2014). Il CcaS è uno SK con un dominio di rilevamento CBCR che assorbe la luce attraverso un cromoforo di ficocianobilina (PCB) covalentemente legato, prodotto da una via metabolica ingegnerizzata. Holo-CcaS è prodotto in uno stato di terra inattivo, verde-sensibile alla luce, chiamato Pg, con bassa attività chinasi. In caso di esposizione alla luce verde, il CcaS Pg passa ad uno stato attivo sensibile alla luce rossa (Pr) con elevata attività chinasi verso il RR CcaR. CcaR~P si lega al promotore PcpcG2-172, attivazione della trascrizione. La luce rossa spinge CcaS Pr a tornare a Pg. Cph8 è uno SK chimerico contenente il dominio di rilevamento della luce Phy PCB-binding Phy di Synechocystis PCC6803 Cph1 e il dominio di segnalazione di E. coli EnvZ. A differenza della CcaS, Cph8 ha un’alta attività chinasi verso l’E. coli RR OmpR nello stato di terra (Pr) e una bassa attività chinasi (alta fosfatasi) in uno stato attivo ad assorbimento di rosso lontano (Pfr). OmpR~P lega e attiva la trascrizione dal PompF146 promotore. I dati del nostro gruppo e di altri suggeriscono che il CcaS Pr è stabile per ore o più (Hirose et al, 2008; Olson et al , 2014), mentre il Cph8 Pfr è molto meno stabile (Olson et al, 2014).
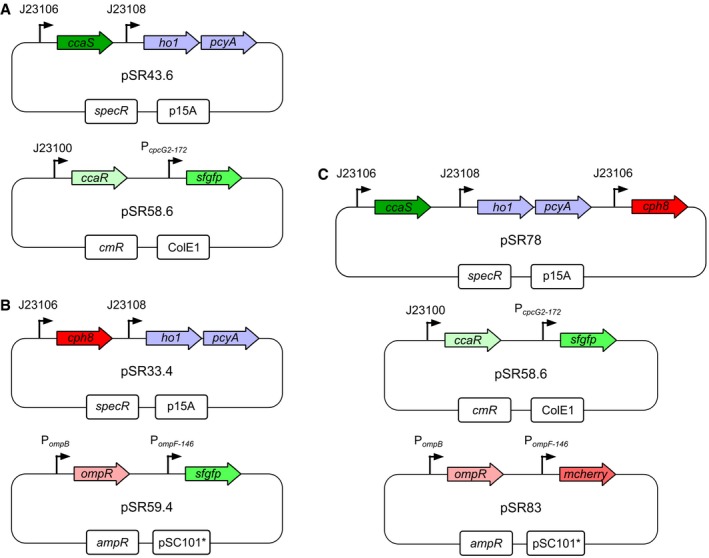
Figura EV1.CcaSR, Cph8-OmpR e mappe plasmidiche a doppio sistema
Mappe dei plasmidi pSR43.6 (in alto) e pSR58.6 (in basso) che esprimono il sistema CcaSR, compresi gli enzimi biosintetici PCB ho1 e pcyA2.Mappe dei plasmidi pSR33.4 (in alto) e pSR59.4 (in basso) che esprime il sistema Cph8-OmpR.Maps of plasmids pSR78 (in alto), pSR58.6 (al centro) e pSR83 (in basso) utilizzati negli esperimenti del sistema duale. Sono disponibili informazioni sulla sequenza dei plasmidi(Dataset EV1).Mappe dei plasmidi pSR43.6 (in alto) e pSR58.6 (in basso) che esprimono il sistema CcaSR, compresi gli enzimi biosintetici PCB ho1 e pcyA2.Mappe dei plasmidi pSR33.4 (in alto) e pSR59.4 (in basso) che esprimono il sistema Cph8-OmpR.Mappe dei plasmidi pSR78 (in alto), pSR58.6 (al centro) e pSR83 (in basso) utilizzate negli esperimenti del sistema duale. Sono disponibili informazioni sulla sequenza dei plasmidi(Dataset EV1).
Recentemente, abbiamo sviluppato un modello fenomenologico predittivo per descrivere le risposte della CcaSR e Cph8-OmpR ai segnali di intensità della luce verde e rossa, rispettivamente (Olson et al, 2014). Questo modello descrive una risposta in tre fasi che comprende un puro ritardo, una transizione di primo ordine dipendente dall’intensità nel tasso di espressione del gene di uscita e una transizione di primo ordine nella concentrazione del gene di uscita impostata in base al tasso di crescita cellulare. Misurando l’espressione di un gene reporter nel tempo in risposta ad una serie di cambi di fase della luce di diverse intensità iniziali e finali, abbiamo parametrizzato questi tre tempi per entrambi i sensori di luce.
Nonostante il suo potere predittivo, il nostro modello precedente ha diversi limiti fondamentali. In primo luogo, può solo prevedere le risposte degli strumenti optogenetici alle specifiche sorgenti luminose utilizzate durante la parametrizzazione. In secondo luogo, non può tenere conto delle perturbazioni introdotte da fonti di luce secondarie come quelle che potrebbero essere utilizzate per la misurazione simultanea di proteine fluorescenti reporter o il controllo multiplexato di entrambi gli strumenti nella stessa cella. In terzo luogo, il modello fornisce poche intuizioni sull’origine meccanicistica delle dinamiche di risposta osservate. Per esempio, ha catturato, ma non ha potuto chiarire l’origine della nostra osservazione che il tasso di transizione dell’espressione genica dipende dalla direzione e dall’intensità finale del cambiamento di fase della luce.
Un modello in vitro (cioè di proteine purificate) (Butler et al, 1964; Sager et al , 1988; Giraud et al, 2010) che descrive l’intensità e la dipendenza dalla lunghezza d’onda della commutazione tra stato di terra e stato attivo è stato precedentemente utilizzato per descrivere il fotoswitching di Phys (Butler et al, 1964; Sager et al, 1988; Giraud et al, 2010). al, 1964), CBCR (Rockwell et al, 2012) , batteriofito-cromi (Giraud et al, 2010), domini LOV(Swartz et al, 2001), e crittocromie (Liu et al, 2008) tra gli altri. In questo modello, i sensori sono caratterizzati dalle loro sezioni d’urto di fotoconversione a terra e a stato attivo (PCS), σg(λ ) e σa(λ ), che permettono ilcalcolo diretto delle velocità di fotoconversione in avanti e indietro, k1 e k2, in risposta ai fotoni di lunghezza d’onda λ. Data la conoscenza di entrambi i PCS(σi (λ)), si può calcolare sia la velocità di fotoconversione (ki) per una sorgente di luce con una nota densità di flusso spettrale luce (λ )(μmol m-2 s-1 nm-1) calcolando la sovrapposizione spettrale integrale ki=∫σi-nlightdλ. I tassi di fotoconversione possono poi essere utilizzati, insieme al tasso di “inversione scura” del fotorecettore indipendente dalla luce (kdr) per calcolare le popolazioni di fotorecettori a terra e a stato attivo.
Nonostante il suo potenziale di previsione delle risposte del fotorecettore a qualsiasi condizione di luce, il modello a due stati di cui sopra non è stato esplorato per l’optogenetica. In particolare, il σi(λ) completo non è stato determinato per nessun fotorecettore optogenetico. Mentre lo spettro di assorbanza è spesso ben stabilito per questi sensori tramite misure in vitro, la dipendenza spettrale della resa quantistica (cioè la probabilità di fotoconversione dato che un fotone è stato assorbito) non lo è. Tuttavia, anche se si dovesse determinare σi(λ), per calcolare le popolazioni di fotorecettori a terra e a stato attivo, il modello dovrebbe essere esteso per catturare la produzione di fotorecettori e le dinamiche di decadimento nelle cellule viventi. Infine, sarebbe necessario un modello aggiuntivo per catturare gli eventi biologici che si verificano a valle del fotorecettore.
Qui, sviluppiamo, parametrizziamo sperimentalmente e dimostriamo le capacità predittive di un modello TCS optogenetico in vivo. In particolare, per prima cosa, estendiamo il modello a due stati per l’ambiente in vivo, e integriamo descrizioni semplificate della segnalazione TCS e dell’espressione genica in uscita, al fine di catturare la completa trasduzione del segnale luce-gene-prodotto. Successivamente, sviluppiamo un set standard di esperimenti di caratterizzazione spettrale e dinamica utilizzando il nostro strumento open-source Light Plate Apparatus (LPA) (Gerhardt et al, 2016) che consente la parametrizzazione del modello sia per CcaSR che per Cph8-OmpR e la stima di σi(λ ) in vivo. Convalidiamo il nostro approccio utilizzando il modello per prevedere accuratamente la risposta di espressione genica di entrambi i sistemi ad una serie di programmi di luce spettralmente e dinamicamente diversificati molto diversi da quelli utilizzati per la parametrizzazione. Infine, esprimiamo CcaSR e Cph8-OmpR nella stessa cellula e combiniamo i modelli con il nostro approccio di generatore di funzioni biologiche per superare la loro intrinseca cross-reattività spettrale e dimostrare la programmazione multiplexata delle dinamiche di espressione genica.

Figura EV1.CcaSR, Cph8-OmpR e mappe plasmidiche a doppio sistema
Mappe dei plasmidi pSR43.6 (in alto) e pSR58.6 (in basso) che esprimono il sistema CcaSR, compresi gli enzimi biosintetici PCB ho1 e pcyA2.Mappe dei plasmidi pSR33.4 (in alto) e pSR59.4 (in basso) che esprime il sistema Cph8-OmpR.Maps of plasmids pSR78 (in alto), pSR58.6 (al centro) e pSR83 (in basso) utilizzati negli esperimenti del sistema duale. Sono disponibili informazioni sulla sequenza dei plasmidi(Dataset EV1).Mappe dei plasmidi pSR43.6 (in alto) e pSR58.6 (in basso) che esprimono il sistema CcaSR, compresi gli enzimi biosintetici PCB ho1 e pcyA2.Mappe dei plasmidi pSR33.4 (in alto) e pSR59.4 (in basso) che esprimono il sistema Cph8-OmpR.Mappe dei plasmidi pSR78 (in alto), pSR58.6 (al centro) e pSR83 (in basso) utilizzate negli esperimenti del sistema duale. Sono disponibili informazioni sulla sequenza dei plasmidi(Dataset EV1).
Risultati
Modello TCS optogenetico
Abbiamo costruito un modello optogenetico in vivo TCS composto da un “modello di rilevamento”, che converte gli ingressi della luce in un rapporto delle popolazioni di fotorecettori, e un “modello di uscita” che converte le popolazioni di fotorecettori in un segnale di espressione genica. Il modello di rilevamento(Materiali e Metodi) estende il modello di fotoconversione in vitro a due stati per includere i termini per la produzione di nuovi fotorecettori a terra (Sg) al tasso kS e la diluizione di entrambi gli Sg e fotorecettori a stato attivo (Sa) alla velocità di kdilal modello a due stati (Fig 1A). Il modello di rilevamento accetta qualsiasi ingresso nlight(λ ) e produce Sg e Sa popolazioni come uscita (fig. 1BeC). Il rapporto Sa/Sg alimenta un “modello di uscita” che comprende una descrizione fenomenologica della segnalazione TCS e un modello standard di espressione genica di uscita (Fig 1C). Il modello di segnalazione TCS(Materiali e Metodi) descrive un puro ritardo temporale(τ ) e la mappatura della funzione Hill kG(x)=b^+a^-xn/(Kn+xn) tra x = Sa/Sg e il tasso di produzione del gene di uscita(kG). Nei nostri esperimenti iniziali, utilizziamo la supercartella GFP(G) come output e quantifichiamo il suo livello di espressione in Molecole di Fluoresceina Equivalente (MEFL) (Castillo-Hair et al, 2016). a^ è la gamma di possibili kG b^ è il valore minimo di kG n è il coefficiente Hill, e K è il Sa/Sg con il risultato di una risposta massima del sistema del 50%. Insieme, questi termini catturano l’autofosforilazione SK, il fosfotransferimento, la dimerizzazione RR, il legame del DNA, l’attivazione del promotore e la produzione di GFP. GFP è degradata in un processo di primo ordine con tasso kdil(Materiali e Metodi) e ha una concentrazione minima b=b^/kdil e intervallo di concentrazione a=a^/kdil dato un tasso di crescita cellulare costante.
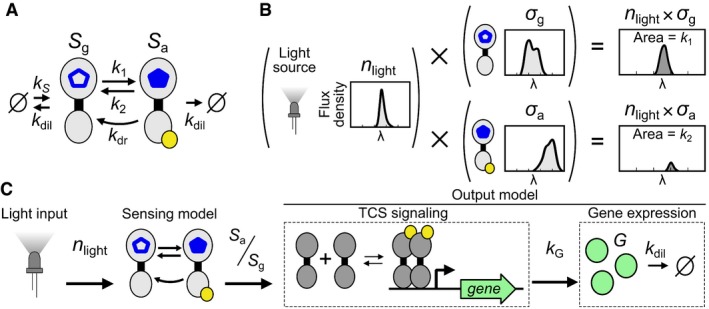
Figura 1.Modello TCS optogenetico
Il modello di fotorecettore a due stati, che comprende il modello a terra e quello a stato attivo (Sg e Sa) fotorecettori (alias sensori), velocità di fotoconversione k1e k2, e velocità di inversione scura kdr, viene convertito in un “modello di rilevamento” per ambienti in vivo aggiungendo un Sg tasso di produzione kS che cattura sia l’espressione genica che la formazione di oloproteine, e un tasso di diluizione kdilper entrambi Sa e Sg a causa della crescita delle cellule e della degradazione del sensore(Materiali e metodi). Il pentagono blu cavo rappresenta un cromoforo allo stato di terra, mentre il pentagono blu riempito rappresenta quello allo stato attivato.le velocità di fotoconversione sono determinate dalla sovrapposizione integrale della densità di flusso spettrale della sorgente luminosa(luce) e dalla densità di flusso Sg e Sa sezioni trasversali di fotoconversione σgeσa (Materialie metodi) Il modello dirilevamento converte la luce leggeranel rapporto attivo dei sensori di luce Sa/Sg che alimenta un “modello di uscita” con un modello semplificato di segnalazione TCS che regola il tasso di produzione kG della proteina G bersaglio, che è diluito a causa della crescita cellulare e proteolisi a tasso kdil(Materiali e Metodi).Il modello del fotorecettore a due stati, che comprende il terreno e lo stato attivo (Sg e Sa) fotorecettori (alias sensori), velocità di fotoconversione k1e k2, e velocità di inversione scura kdr, viene convertito in un “modello di rilevamento” per ambienti in vivo aggiungendo un Sg tasso di produzione kS che cattura sia l’espressione genica che la formazione di oloproteine, e un tasso di diluizione kdilper entrambi Sa e Sg a causa della crescita delle cellule e della degradazione del sensore(Materiali e metodi). Il pentagono blu cavo rappresenta un cromoforo allo stato di terra, mentre il pentagono blu riempito rappresenta quello allo stato attivato.I tassi di fotoconversione sono determinati dalla sovrapposizione integrale della densità di flusso spettrale della sorgenteluminosa (nlight) e della Sg e Sa sezioni trasversali di fotoconversione σgeσa (Materialie metodi).Il modello di rilevamento converte la luce leggeranel rapporto attivo dei sensori di luce Sa/Sg che alimenta un “modello di uscita” con un modello semplificato di segnalazione TCS che regola il tasso di produzione kG della proteina G bersaglio, che è diluito a causa della crescita cellulare e proteolisi a tasso kdil(Materiali e Metodi).

Figura 1.Modello TCS optogenetico
Il modello del fotorecettore a due stati, che comprende il terreno e lo stato attivo (Sg e Sa) fotorecettori (alias sensori), velocità di fotoconversione k1e k2, e velocità di inversione scura kdr, viene convertito in un “modello di rilevamento” per ambienti in vivo aggiungendo un Sg tasso di produzione kS che cattura sia l’espressione genica che la formazione di oloproteine, e un tasso di diluizione kdilper entrambi Sa e Sg a causa della crescita delle cellule e della degradazione del sensore(Materiali e metodi). Il pentagono blu cavo rappresenta un cromoforo allo stato di terra, mentre il pentagono blu riempito rappresenta quello allo stato attivato.le velocità di fotoconversione sono determinate dalla sovrapposizione integrale della densità di flusso spettrale della sorgente luminosa(luce) e dalla densità di flusso Sg e Sa sezioni trasversali di fotoconversione σgeσa (Materialie metodi) Il modello dirilevamento converte la luce leggeranel rapporto attivo dei sensori di luce Sa/Sg che alimenta un “modello di uscita” con un modello semplificato di segnalazione TCS che regola il tasso di produzione kG della proteina G bersaglio, che è diluito a causa della crescita cellulare e proteolisi a tasso kdil(Materiali e Metodi).Il modello del fotorecettore a due stati, che comprende il terreno e lo stato attivo (Sg e Sa) fotorecettori (alias sensori), velocità di fotoconversione k1e k2, e velocità di inversione scura kdr, viene convertito in un “modello di rilevamento” per ambienti in vivo aggiungendo un Sg tasso di produzione kS che cattura sia l’espressione genica che la formazione di oloproteine, e un tasso di diluizione kdilper entrambi Sa e Sg a causa della crescita delle cellule e della degradazione del sensore(Materiali e metodi). Il pentagono blu cavo rappresenta un cromoforo allo stato di terra, mentre il pentagono blu riempito rappresenta quello allo stato attivato.I tassi di fotoconversione sono determinati dalla sovrapposizione integrale della densità di flusso spettrale della sorgenteluminosa (nlight) e della Sg e Sa sezioni trasversali di fotoconversione σgeσa (Materialie metodi).Il modello di rilevamento converte la luce leggeranel rapporto attivo dei sensori di luce Sa/Sg che alimenta un “modello di uscita” con un modello semplificato di segnalazione TCS che regola il tasso di produzione kG della proteina G bersaglio, che è diluito a causa della crescita cellulare e proteolisi a tasso kdil(Materiali e Metodi).
Modello di sorgente luminosa
La maggior parte delle sorgenti luminose hanno una densità di flusso spettrale fissa (cioè lo spettro di uscita) che si scala con l’intensità della luce(I, μmol m-2 s-1). Per tali sorgenti luminose, possiamo scrivere nlight=n^luce-I dove n^luce è lo spettro di uscita a 1 μmol m-2 s-1. Per quantificare la sovrapposizione tra nlight e σi per un dato fotorecettore, introduciamo k^i come tasso di fotoconversione per unità di intensità luminosa (min-1[μmol m-2 s-1]-1). Poi, per una data sorgente di luce, ki=I-∫σi-n^lightdλ=I-k^i. Cioè, k1e k2assumono valori proporzionali all’intensità della luce.
Caratterizzazione dinamica e spettrale della CcaSR
Abbiamo progettato una serie di quattro semplici esperimenti di caratterizzazione dell’espressione genica per addestrare il modello optogenetico TCS per la CcaSR (Fig 2A-E, Dataset EV2, e Appendice Metodi S1 e S2). In primo luogo, quantifichiamo la dinamica di attivazione precondizionando l ‘E. coli che esprime la CcaSR al buio, introducendo aumenti di fase in luce verde (lunghezza d’onda centroide λc= 526 nm, (Tabelle EV1, EV2 ed EV3 , Dataset EV3 , e Appendice Metodo S3) a diverse intensità, e misurando i livelli di sfGFP nel tempo con la citometria a flusso (Materiali e Metodi, Fig 2B, e Appendice Fig S1). In secondo luogo, misuriamo le dinamiche di disattivazione precondizionando le cellule in diverse intensità di luce verde e misurando la risposta al passo diminuisce fino al buio (Fig 2Ce Appendice Fig S1). In terzo luogo, misuriamo la risposta spettrale dello stato del suolo esponendo i batteri a 23 LED con λc che coprono 369-958 nm con intensità di illuminazione che variano su tre ordini di grandezza (Materialie Metodi, Fig 2D, Appendice Fig S2 , Tabelle EV1, EV2 ed EV3, e Appendice Metodo S3) e misurando sfGFP allo stato stazionario. Infine, misuriamo la risposta spettrale allo stato attivato ripetendo l’esperimento precedente in presenza di una intensità costante della luce attiva (Fig 2Ee Appendice Fig S2).
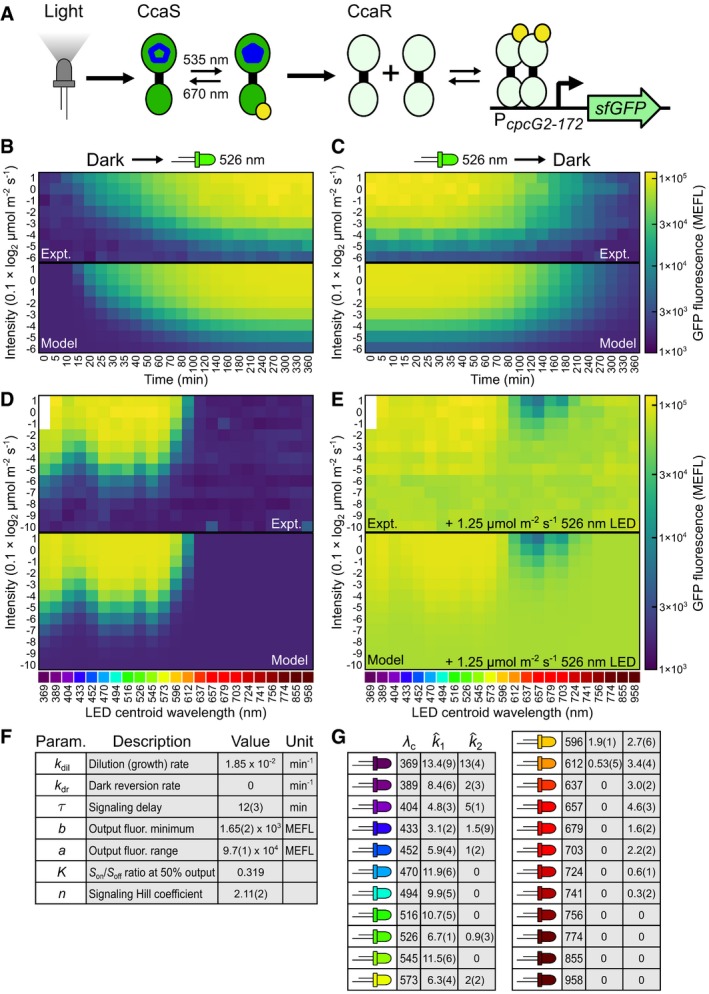
F, G.Caratterizzazione e parametrizzazione del modello per la CcaSR
ASchematic di CcaSR TCS con uscita sfGFP. I valori di lunghezza d’onda rappresentano i dati di assorbanza misurati in vitro maxima.B-ETraining per il modello completo del sistema CcaSR (Fig 1C). Le osservazioni sperimentali (“Expt.”) e le simulazioni del modello più adatto (“Model”) sono mostrate per ogni set. In particolare, la dinamica di risposta al passo (B) aumenta da scuro a otto diverse intensità e (C) diminuisce da otto diverse intensità a scuro sono stati valutati utilizzando la λc= 526 nm LED. I punti temporali sono distribuiti in modo non uniforme per aumentare la risoluzione della risposta iniziale. (D, E) Steady-state intensità dose-risposta ad un insieme di 23 “LED spettrali” con λc che vanno da 369 nm a 958 nm. (D) La fotoconversione in avanti è determinata principalmente dalla risposta ai LED spettrali. (E) La fotoconversione inversa è analizzata includendo la luce di un secondo, attivando il LED(λc= 526 nm a 1,25 μmol m-2 s-1). La λc= 369 nm LED non è in grado di raggiungere le intensità più brillanti, e quindi questi punti dati non sono inclusi. Le intensità di luce sono mostrate in unità di 0,1 × log2 μmol m-2 s-1 scala (ad es, un valore di 1 corrisponde a 10 × 21 = 20 μmol m-2 s-1). la fluorescenza sfGFP è calibrata su unità MEFL (Materiali e metodi). Ogni fila di misure in pannelli (B-E) è stata raccolta in una singola piastra a 24 pozzetti. Le 40 piastre necessarie per produrre il dataset di formazione sono state distribuite in modo casuale su otto LPA in cinque studi separati(Materiali e Meto di e Dataset EV2). Ogni piastra di colore rappresenta la media aritmetica di una singola popolazione di cellule.F, parametri del modello GBest-fit prodotti tramite regressione non lineare del modello ai dati di training (Materiali e Meto di e Tabella EV4). k ^i sono i tassi di fotoconversione unitaria (10-3 × min-1/(μmol m-2 s-1), cioè, ki = I-k^i, dove I è l’intensità del LED in μmol m-2 s-1). L’incertezza nelle cifre meno significative è indicata tra parentesi.Schema del TCS CcaSR con uscita sfGFP. I valori di lunghezza d’onda rappresentano i massimi di assorbanza misurati in vitro.Dati di formazione per il modello completo del sistema CcaSR (Fig 1C). Le osservazioni sperimentali (“Expt.”) e le simulazioni del modello più adatto (“Modello”) sono mostrate per ogni set. In particolare, la dinamica di risposta al passo (B) aumenta da scuro a otto diverse intensità e (C) diminuisce da otto diverse intensità a scuro sono stati valutati utilizzando la λc= 526 nm LED. I punti temporali sono distribuiti in modo non uniforme per aumentare la risoluzione della risposta iniziale. (D, E) Steady-state intensità dose-risposta ad un insieme di 23 “LED spettrali” con λc che vanno da 369 nm a 958 nm. (D) La fotoconversione in avanti è determinata principalmente dalla risposta ai LED spettrali. (E) La fotoconversione inversa è analizzata includendo la luce di un secondo, attivando il LED(λc= 526 nm a 1,25 μmol m-2 s-1). La λc= 369 nm LED non è in grado di raggiungere le intensità più brillanti, e quindi questi punti dati non sono inclusi. Le intensità di luce sono mostrate in unità di 0,1 × log2 μmol m-2 s-1 scala (ad es, un valore di 1 corrisponde a 10 × 21 = 20 μmol m-2 s-1). la fluorescenza sfGFP è calibrata su unità MEFL (Materiali e metodi). Ogni fila di misure in pannelli (B-E) è stata raccolta in una singola piastra a 24 pozzetti. Le 40 piastre necessarie per produrre il dataset di formazione sono state distribuite in modo casuale su otto LPA in cinque studi separati(Materiali e Meto di e Dataset EV2). Ogni piastra di colore rappresenta la media aritmetica di una singola popolazione di cellule.Parametri del modello più adatto prodotti attraverso la regressione non lineare del modello ai dati di addestramento (Materiali e Metodi e Tabella EV4). k^i sono velocità di fotoconversione unitaria (10-3 × min-1/(μmol m-2 s-1), cioè ki=I-k^i, dove I è l’intensità del LED in μmol m-2 s-1). L’incertezza nelle cifre meno significative è indicata tra parentesi.

F, G.Caratterizzazione e parametrizzazione del modello per la CcaSR
ASchematic di CcaSR TCS con uscita sfGFP. I valori di lunghezza d’onda rappresentano i dati di assorbanza misurati in vitro maxima.B-ETraining per il modello completo del sistema CcaSR (Fig 1C). Le osservazioni sperimentali (“Expt.”) e le simulazioni del modello più adatto (“Model”) sono mostrate per ogni set. In particolare, la dinamica di risposta al passo (B) aumenta da scuro a otto diverse intensità e (C) diminuisce da otto diverse intensità a scuro sono stati valutati utilizzando la λc= 526 nm LED. I punti temporali sono distribuiti in modo non uniforme per aumentare la risoluzione della risposta iniziale. (D, E) Steady-state intensità dose-risposta ad un insieme di 23 “LED spettrali” con λc che vanno da 369 nm a 958 nm. (D) La fotoconversione in avanti è determinata principalmente dalla risposta ai LED spettrali. (E) La fotoconversione inversa è analizzata includendo la luce di un secondo, attivando il LED(λc= 526 nm a 1,25 μmol m-2 s-1). La λc= 369 nm LED non è in grado di raggiungere le intensità più brillanti, e quindi questi punti dati non sono inclusi. Le intensità di luce sono mostrate in unità di 0,1 × log2 μmol m-2 s-1 scala (ad es, un valore di 1 corrisponde a 10 × 21 = 20 μmol m-2 s-1). la fluorescenza sfGFP è calibrata su unità MEFL (Materiali e metodi). Ogni fila di misure in pannelli (B-E) è stata raccolta in una singola piastra a 24 pozzetti. Le 40 piastre necessarie per produrre il dataset di formazione sono state distribuite in modo casuale su otto LPA in cinque studi separati(Materiali e Meto di e Dataset EV2). Ogni piastra di colore rappresenta la media aritmetica di una singola popolazione di cellule.F, parametri del modello GBest-fit prodotti tramite regressione non lineare del modello ai dati di training (Materiali e Meto di e Tabella EV4). k ^i sono i tassi di fotoconversione unitaria (10-3 × min-1/(μmol m-2 s-1), cioè, ki = I-k^i, dove I è l’intensità del LED in μmol m-2 s-1). L’incertezza nelle cifre meno significative è indicata tra parentesi.Schema del TCS CcaSR con uscita sfGFP. I valori di lunghezza d’onda rappresentano i massimi di assorbanza misurati in vitro.Dati di formazione per il modello completo del sistema CcaSR (Fig 1C). Le osservazioni sperimentali (“Expt.”) e le simulazioni del modello più adatto (“Modello”) sono mostrate per ogni set. In particolare, la dinamica di risposta al passo (B) aumenta da scuro a otto diverse intensità e (C) diminuisce da otto diverse intensità a scuro sono stati valutati utilizzando la λc= 526 nm LED. I punti temporali sono distribuiti in modo non uniforme per aumentare la risoluzione della risposta iniziale. (D, E) Steady-state intensità dose-risposta ad un insieme di 23 “LED spettrali” con λc che vanno da 369 nm a 958 nm. (D) La fotoconversione in avanti è determinata principalmente dalla risposta ai LED spettrali. (E) La fotoconversione inversa è analizzata includendo la luce di un secondo, attivando il LED(λc= 526 nm a 1,25 μmol m-2 s-1). La λc= 369 nm LED non è in grado di raggiungere le intensità più brillanti, e quindi questi punti dati non sono inclusi. Le intensità di luce sono mostrate in unità di 0,1 × log2 μmol m-2 s-1 scala (ad es, un valore di 1 corrisponde a 10 × 21 = 20 μmol m-2 s-1). la fluorescenza sfGFP è calibrata su unità MEFL (Materiali e metodi). Ogni fila di misure in pannelli (B-E) è stata raccolta in una singola piastra a 24 pozzetti. Le 40 piastre necessarie per produrre il dataset di formazione sono state distribuite in modo casuale su otto LPA in cinque studi separati(Materiali e Meto di e Dataset EV2). Ogni piastra di colore rappresenta la media aritmetica di una singola popolazione di cellule.Parametri del modello più adatto prodotti attraverso la regressione non lineare del modello ai dati di addestramento (Materiali e Metodi e Tabella EV4). k^i sono velocità di fotoconversione unitaria (10-3 × min-1/(μmol m-2 s-1), cioè ki=I-k^i, dove I è l’intensità del LED in μmol m-2 s-1). L’incertezza nelle cifre meno significative è indicata tra parentesi.
Parametrizzazione del modello CcaSR
Successivamente, abbiamo usato la regressione non lineare per adattare il modello ai dati di caratterizzazione dinamica e spettrale(Materiali e Metodi, Tabella EV4, e Dataset EV2). In particolare, abbiamo determinato i valori k^1 e k^2 per ogni LED, e i valori (indipendenti dai LED) dei parametri della funzione Hill, kdil,kdr,e τ per il sistema (Fig 2F e G). Mentre le simulazioni che utilizzano i parametri best-fit risultanti (Fig 2B-E, Dataset EV4, e Tabella EV4) ricapitolano le proprietà note del sistema (Appendice Fig S3),il valore del parametro Hill K è debolmente determinato. In particolare, le alterazioni di K rispetto al valore best-fit possono essere compensate da variazioni di k^1 e k^2 (Appendice Fig S4). Pertanto, non possiamo determinare con sicurezza i tassi assoluti di fotoconversione in avanti e all’indietro. Tuttavia, fissando K al suo valore di best-fit si ottengono previsioni del modello che concordano quantitativamente con le misure sperimentali (Fig 2B-EeAppendice Fig S3).
Convalida spettrale del modello di fotoconversione CcaSR
I nostri esperimenti di parametrizzazione forniscono valori k^1 e k^2 per ogni LED di calibrazione (Fig 2G). Tuttavia, per prevedere la risposta di uno strumento optogenetico ad una nuova sorgente luminosa senza ulteriori esperimenti di calibrazione, la conoscenza di σi è richiesta. Per stimare σi per la CcaSR, abbiamo sviluppato una procedura per adattare una spline cubica ai valori precedentemente determinati k^1 e k^2 per ciascuno dei 23 LED(Materiali e Metodi, Fig 3A, Appendice Figs S5 e S6, e Dataset EV2 ed EV5). È importante notare che la nostra procedura di regressione considera la risposta della CcaSR all’intera emissione spettrale di ogni LED, non solo la sua lunghezza d’onda centroide. Per convalidare il risultato σi abbiamo misurato n^luce(λ) per un set non testato in precedenza di otto LED a luce bianca filtrata a colori, progettati per avere caratteristiche spettrali complesse (Tabelle EV1, EV2 ed EV3, Dataset EV3, e Appendice Metodo S3) e calcolato un k^i previsto per ciascuno di essi (Fig 3B). In combinazione con i rimanenti parametri del modello (Fig 2F), abbiamo usato questi k^i per predire la dose-risposta dell’intensità allo stato stazionario a questi otto LED in presenza e in assenza di luce attiva (λc= 526 nm). Queste previsioni sono notevolmente accurate per i LED 1-5 (errori radice-media-quadrato (RMSE) da 0,13 a 0,22, Materiali e Metodi), che guidano sfGFP ad alti livelli, e 7 e 8, che guidano bassa espressione (RMSE = 0.17 e 0.14, rispettivamente), ma un po’ meno per il LED 6 (RMSE = 0.28), che guida sfGFP ad un livello di espressione intermedio (Fig 3C). Questi risultati dimostrano che possiamo prevedere la risposta della CcaSR ad una vasta gamma di sorgenti luminose non testate in precedenza utilizzando solo misurazioni spettroradiometriche della loro n^luce(λ) e non esperimenti di calibrazione biologica.
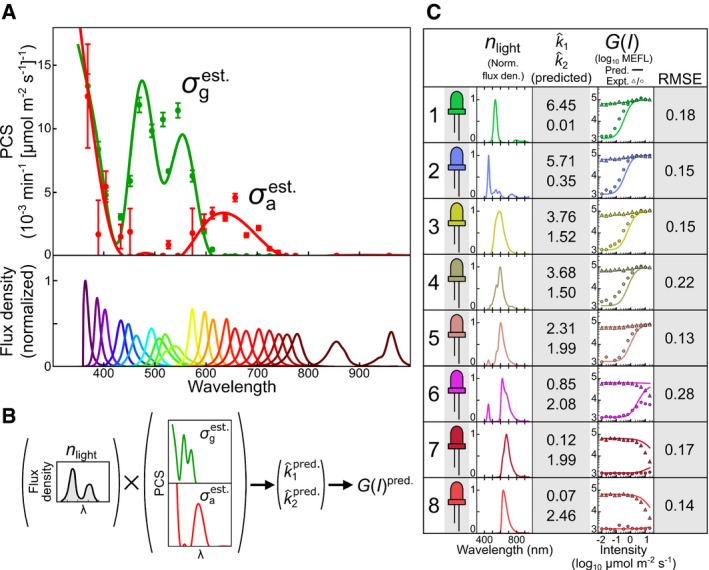
Figura 3.Stima della sezione d’urto della fotoconversione CcaS e convalida spettrale del modello CcaSR
Stimiamo i PCS continui a terra e a stato attivo di CcaS (σiest., linee) attraverso la regressione di spline cubiche per ridurre al minimo la differenza tra i tassi di fotoconversione (punti) determinati sperimentalmente e quelli previsti tramite k ^ipred.=∫σiest.-n^lighttdλ (Materiali e Metodi, AppendiceFigs S5 e S6, e Dataset EV5). Le barre di errore indicano l’errore standard dei valori di best-fit dei tassi di fotoconversione che sono stati determinati durante la parametrizzazione del modello della CcaSR (Fig 2). Le densità di flusso spettrale normalizzate dei LED spettrali sono mostrate in basso, utilizzando σiest. per prevedere i tassi di fotoconversione per le sorgenti luminose non presenti nel set di formazione dei LED spettrali. I tassi di fotoconversione previsti sono integrati nel modello CcaSR mantenendo tutti gli altri parametri (Fig 2F) fissi, consentendo di prevedere l’intensità dose-risposta della CcaSR alla nuova sorgente di luce (ad es, G(I)pred.).La validazione spettrale del modello CcaSR e σiest. consiste nella previsione della dose-risposta dell’intensità per otto sorgenti luminose impegnative ad ampio spettro costruite applicando filtri colorati su LED a luce bianca (Materiali eMetodi, Tabelle EV1, EV2 ed EV3, e Dataset EV3). Per ogni LED (Materiali e Metodi) sono mostrate le curve di dose-risposta dell‘intensità misurata e prevista e RMSE tra modello e previsione. Le risposte di intensità in avanti e indietro sono determinate usando il solo LED filtrato (cerchi) e in presenza di un secondo LED di attivazione(λc= 526 nm a 1,25 μmol m-2 s-1, triangoli). Le risposte simulate sono determinate utilizzando i tassi di fotoconversione calcolati(Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti attraverso quattro LPA, e le risposte di intensità in avanti (cerchi) e indietro (triangoli) sono state raccolte su due prove sperimentali separate(Materiali e Metodi e Dataset EV2). Ogni punto di dati rappresenta la media aritmetica di una singola popolazione di cellule.Stimiamo i PCS continui a terra e a stato attivo del CcaS (σiest., linee) mediante la regressione di spline cubiche per minimizzare la differenza tra i tassi di fotoconversione (punti) determinati sperimentalmente e quelli previsti tramite k^ipred.=∫σiest.-n^lucetdλ (Materiali e Metodi, AppendiceFigs S5 e S6, e Dataset EV5). Le barre di errore indicano l’errore standard dei valori di best-fit dei tassi di fotoconversione che sono stati determinati durante la parametrizzazione del modello della CcaSR (Fig 2). Le densità di flusso spettrale normalizzate dei LED spettrali sono indicate in basso.Utilizzando σiest. per prevedere i tassi di fotoconversione per le sorgenti luminose non presenti nel set di formazione dei LED spettrali. I tassi di fotoconversione previsti sono integrati nel modello CcaSR mantenendo tutti gli altri parametri (Fig 2F) fissi, consentendo di prevedere l’intensità dose-risposta della CcaSR alla nuova sorgente di luce (cioè, G(I)pred. ).La validazione spettrale del modello CcaSR e σiest. consiste nella previsione della dose-risposta dell’intensità per otto stimolanti sorgenti luminose ad ampio spettro costruite applicando filtri colorati su LED a luce bianca (Materiali e Metodi, Tabelle EV1, EV2 ed EV3, e Dataset EV3). Per ogni LED (Materiali e Metodi) sono mostrate le curve di dose-risposta dell‘intensità misurata e prevista e RMSE tra modello e previsione. Le risposte di intensità in avanti e indietro sono determinate usando il solo LED filtrato (cerchi) e in presenza di un secondo LED di attivazione(λc= 526 nm a 1,25 μmol m-2 s-1, triangoli). Le risposte simulate sono determinate utilizzando i tassi di fotoconversione calcolati(Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti attraverso quattro LPA, e le risposte di intensità in avanti (cerchi) e indietro (triangoli) sono state raccolte su due prove sperimentali separate(Materiali e Metodi e Dataset EV2). Ogni punto di dati rappresenta la media aritmetica di una singola popolazione di cellule.

Figura 3.Stima della sezione d’urto della fotoconversione CcaS e convalida spettrale del modello CcaSR
Stimiamo i PCS continui a terra e a stato attivo di CcaS (σiest., linee) attraverso la regressione di spline cubiche per ridurre al minimo la differenza tra i tassi di fotoconversione (punti) determinati sperimentalmente e quelli previsti tramite k^ipred.=∫σiest.-n^lighttdλ (Materiali e Metodi, AppendiceFigs S5 e S6, e Dataset EV5). Le barre di errore indicano l’errore standard dei valori di best-fit dei tassi di fotoconversione che sono stati determinati durante la parametrizzazione del modello della CcaSR (Fig 2). Le densità di flusso spettrale normalizzate dei LED spettrali sono mostrate in basso, utilizzando σiest. per prevedere i tassi di fotoconversione per le sorgenti luminose non presenti nel set di formazione dei LED spettrali. I tassi di fotoconversione previsti sono integrati nel modello CcaSR mantenendo tutti gli altri parametri (Fig 2F) fissi, consentendo di prevedere l’intensità dose-risposta della CcaSR alla nuova sorgente di luce (ad es, G(I)pred.).La validazione spettrale del modello CcaSR e σiest. consiste nella previsione della dose-risposta dell’intensità per otto sorgenti luminose impegnative ad ampio spettro costruite applicando filtri colorati su LED a luce bianca (Materiali eMetodi, Tabelle EV1, EV2 ed EV3, e Dataset EV3). Per ogni LED (Materiali e Metodi) sono mostrate le curve di dose-risposta dell‘intensità misurata e prevista e RMSE tra modello e previsione. Le risposte di intensità in avanti e indietro sono determinate usando il solo LED filtrato (cerchi) e in presenza di un secondo LED di attivazione(λc= 526 nm a 1,25 μmol m-2 s-1, triangoli). Le risposte simulate sono determinate utilizzando i tassi di fotoconversione calcolati(Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti attraverso quattro LPA, e le risposte di intensità in avanti (cerchi) e indietro (triangoli) sono state raccolte su due prove sperimentali separate(Materiali e Metodi e Dataset EV2). Ogni punto di dati rappresenta la media aritmetica di una singola popolazione di cellule.Stimiamo i PCS continui a terra e a stato attivo del CcaS (σiest., linee) mediante la regressione di spline cubiche per minimizzare la differenza tra i tassi di fotoconversione (punti) determinati sperimentalmente e quelli previsti tramite k^ipred.=∫σiest.-n^lucetdλ (Materiali e Metodi, AppendiceFigs S5 e S6, e Dataset EV5). Le barre di errore indicano l’errore standard dei valori di best-fit dei tassi di fotoconversione che sono stati determinati durante la parametrizzazione del modello della CcaSR (Fig 2). Le densità di flusso spettrale normalizzate dei LED spettrali sono indicate in basso.Utilizzando σiest. per prevedere i tassi di fotoconversione per le sorgenti luminose non presenti nel set di formazione dei LED spettrali. I tassi di fotoconversione previsti sono integrati nel modello CcaSR mantenendo tutti gli altri parametri (Fig 2F) fissi, consentendo di prevedere l’intensità dose-risposta della CcaSR alla nuova sorgente di luce (cioè, G(I)pred. ).La validazione spettrale del modello CcaSR e σiest. consiste nella previsione della dose-risposta dell’intensità per otto stimolanti sorgenti luminose ad ampio spettro costruite applicando filtri colorati su LED a luce bianca (Materiali e Metodi, Tabelle EV1, EV2 ed EV3, e Dataset EV3). Per ogni LED (Materiali e Metodi) sono mostrate le curve di dose-risposta dell‘intensità misurata e prevista e RMSE tra modello e previsione. Le risposte di intensità in avanti e indietro sono determinate usando il solo LED filtrato (cerchi) e in presenza di un secondo LED di attivazione(λc= 526 nm a 1,25 μmol m-2 s-1, triangoli). Le risposte simulate sono determinate utilizzando i tassi di fotoconversione calcolati(Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti attraverso quattro LPA, e le risposte di intensità in avanti (cerchi) e indietro (triangoli) sono state raccolte su due prove sperimentali separate(Materiali e Metodi e Dataset EV2). Ogni punto di dati rappresenta la media aritmetica di una singola popolazione di cellule.
Convalida dinamica del modello di fotoconversione CcaSR
In precedenza abbiamo sviluppato un metodo “generatore di funzioni biologiche” in cui utilizziamo un modello predittivo per ottimizzare computazionalmente i programmi di ingresso della luce per pilotare segnali di espressione genica su misura come le rampe lineari e le onde sinusoidali (Olson et al, 2014) . Questo metodo costituisce una rigorosa validazione del potere predittivo di un modello perché gli input e gli output di espressione genica della luce sono temporalmente complessi e coprono un’ampia gamma di livelli. Per convalidare il nostro modello di fotoconversione CcaSR, abbiamo prima progettato un segnale di espressione genica di riferimento impegnativo (Fig 4 e Dataset EV6). Il segnale parte da b e poi aumenta linearmente (su scala logaritmica) oltre il 90% del range di risposta CcaSR totale su 210 min. Dopo una pausa di 60 minuti, il segnale diminuisce linearmente fino ad un livello di espressione intermedio su altri 210 min. Abbiamo quindi utilizzato il modello per progettare computazionalmente quattro corsi di tempo di luce ciascuno con diversi LED o miscele di LED per programmare i batteri a seguire questo segnale di riferimento(Materiali e Metodi e Dataset EV6). “UV mono” utilizza un singolo LED UV (λc= 389 nm) (Fig 4A) per dimostrare il controllo della CcaSR con una sorgente luminosa atipica. “Green mono” utilizza il λc= 526 nm LED (Fig 4B) per dimostrare il controllo predittivo con una sorgente luminosa tipica. “Red perturbation” combina “Green mono” con un forte rosso (λc= 657 nm) segnale sinusoidale (Fig 4C e Dataset EV6) progettato per dimostrare gli effetti perturbativi di ulteriori fonti di luce durante gli esperimenti. Infine, in “Red compensation”, il percorso temporale “Green mono” viene ri-ottimizzato per compensare l’impatto della “Perturbazione rossa” (Fig 4D e Materiali e Metodi).
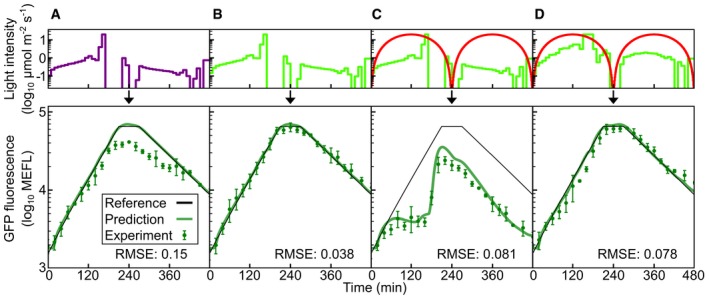
Figura 4.Convalida dinamica del modello CcaSRConfrontiamo le previsioni del modello di uscita dinamica CcaSR sfGFP con le misure sperimentali per gli ingressi di luce variabile nel tempo da UV (linea viola; λc= 389 nm), verde (λc= 526 nm), o verde più rosso (λc= 657 nm) luce. In tutti i casi, i programmi di luce (in alto) sono prodotti utilizzando l’algoritmo del generatore di programmi di luce (GPL, Materiali e Metodi). Il GPL usa il modello del sistema per produrre un programma di luce che guida una simulazione di espressione genica (in basso, linea verde) che corrisponde strettamente al segnale di riferimento (in basso, linea nera). La simulazione (cioè la previsione del modello), viene poi confrontata con la risposta misurata sperimentalmente (in basso, punti di dati). Il segnale di riferimento consiste in una rampa verso l’alto, hold e rampa verso il basso su una scala logaritmica(Dataset EV6).
“UV mono”. Il segnale di luce UV generato dal GPL guida il sistema CcaSR lungo una traiettoria prevista per seguire il segnale di riferimento. “Green mono”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato. “Perturbazione rossa”. Il LED verde fornisce il segnale “Verde mono”, mentre il LED rosso genera un segnale sinusoidale di perturbazione (centro) con un periodo di 240 minuti e 20 μmol m-2 s-1 di ampiezza picco-picco.“ Compensazione rossa”. Il segnale perturbativo rosso è di nuovo presente. Tuttavia, il GPL ridisegna il segnale di luce verde per tener conto della sua presenza: I segnali luminosi sono mostrati in unità di log10 μmol m-2 s-1, e gli errori relativi RMSE sono espressi in log10 decadi (Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali indipendenti(Tabella EV4 e Dataset EV2).“UV mono”. Il segnale di luce UV generato dal GPL guida il sistema CcaSR lungo una traiettoria prevista per seguire il segnale di riferimento.“Verde mono”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato.“Perturbazione rossa”. Il LED verde fornisce il segnale “Verde mono”, mentre il LED rosso genera un segnale perturbativo sinusoidale (centro) con un periodo di 240 minuti e 20 μmol m-2 s-1 di ampiezza da picco a picco.“Compensazione rossa”. Il segnale perturbativo rosso è di nuovo presente. Tuttavia, il GPL ridisegna il segnale di luce verde per tener conto della sua presenza.
Il modello prevede la risposta della CcaSR a tutti e quattro i segnali luminosi con elevata precisione quantitativa (Fig 4 e Dataset EV2). “Mono UV” presenta la sfida più grande, con un RMSE di 0,15 (Fig 4A). Sospettiamo che gli errori di previsione in questo programma sono dovuti alla fotodegradazione del PCB, in quanto non abbiamo osservato alcuna tossicità significativa attraverso il tasso di crescita batterica durante questo esperimento(Appendice Figs S7 e S8), e la previsione rimane accurata fino a quando l’UV raggiunge la massima intensità (20 μmol m-2 s-1). “Green mono” (Fig 4B) determinal‘errore più basso (RMSE = 0,038), che è previsto perché questo LED è stato utilizzato per eseguire le calibrazioni dinamiche (Fig 2B e C). Come previsto, la “Perturbazione rossa” comporta un’enorme deviazione dal segnale di riferimento (Fig 4C), ed il modello prevede accuratamente questo effetto (RMSE = 0,081). Infine, “Red compensation” dimostra che l’effetto della perturbazione può essere eliminato usando il nostro modello (Fig 4D, RMSE = 0,078).

Figura 4.Convalida dinamica del modello CcaSRConfrontiamo le previsioni del modello di uscita dinamica CcaSR sfGFP con le misure sperimentali per gli ingressi di luce variabile nel tempo da UV (linea viola; λc= 389 nm), verde (λc= 526 nm), o verde più rosso (λc= 657 nm) luce. In tutti i casi, i programmi di luce (in alto) sono prodotti utilizzando l’algoritmo del generatore di programmi di luce (GPL, Materiali e Metodi). Il GPL usa il modello del sistema per produrre un programma di luce che guida una simulazione di espressione genica (in basso, linea verde) che corrisponde strettamente al segnale di riferimento (in basso, linea nera). La simulazione (cioè la previsione del modello), viene poi confrontata con la risposta misurata sperimentalmente (in basso, punti di dati). Il segnale di riferimento consiste in una rampa verso l’alto, hold e rampa verso il basso su una scala logaritmica(Dataset EV6).
“UV mono”. Il segnale di luce UV generato dal GPL guida il sistema CcaSR lungo una traiettoria prevista per seguire il segnale di riferimento. “Green mono”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato. “Perturbazione rossa”. Il LED verde fornisce il segnale “Verde mono”, mentre il LED rosso genera un segnale sinusoidale di perturbazione (centro) con un periodo di 240 minuti e 20 μmol m-2 s-1 di ampiezza picco-picco.“ Compensazione rossa”. Il segnale perturbativo rosso è di nuovo presente. Tuttavia, il GPL ridisegna il segnale di luce verde per tener conto della sua presenza: I segnali luminosi sono mostrati in unità di log10 μmol m-2 s-1, e gli errori relativi RMSE sono espressi in log10 decadi (Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali indipendenti(Tabella EV4 e Dataset EV2).“UV mono”. Il segnale di luce UV generato dal GPL guida il sistema CcaSR lungo una traiettoria prevista per seguire il segnale di riferimento.“Verde mono”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato.“Perturbazione rossa”. Il LED verde fornisce il segnale “Verde mono”, mentre il LED rosso genera un segnale perturbativo sinusoidale (centro) con un periodo di 240 minuti e 20 μmol m-2 s-1 di ampiezza da picco a picco.“Compensazione rossa”. Il segnale perturbativo rosso è di nuovo presente. Tuttavia, il GPL ridisegna il segnale di luce verde per tener conto della sua presenza.
Modello di fotoconversione Cph8-OmpR
Per valutare la generalità del nostro approccio, abbiamo ripetuto l’intero flusso di lavoro per Cph8-OmpR (Figg. EV2, EV3,EV4, Appendice Figg. S9, S10 e S11 , Tabella EV5 , e Dataset EV7). Sebbene CcaSR e Cph8-OmpR siano entrambi TCS fotoreversibili, hanno diversi domini fotosensoriali, attività al suolo e dinamiche. Per tenere conto del fatto che il Cph8-OmpR è prodotto in uno stato attivo a terra, abbiamo usato una funzione di repressing Hill nella porzione di segnalazione TCS del modello di uscita (Materiali e Metodi). Il modello si adatta ancora una volta eccezionalmente bene ai dati sperimentali (Fig EV2e Appendice Figs S9, S10, S11). A differenza della CcaSR, che non ha mostrato alcuna reversione scura rilevabile (Fig 2F), laCph8-OmpRsembra revertire in τ1/2=ln2/kdr=5,5min (Fig EV2F). Come prima, K è sottodeterminato(Appendice Fig S4), e abbiamo scelto il valore più adatto (Tabella EV5). Il modello Cph8-OmpR si comporta in modo simile alla sua controparte CcaSR negli esperimenti di validazione spettrale (Fig EV3) e dimostra un maggiore controllo predittivo negli esperimenti di validazione dinamica (Fig EV4).
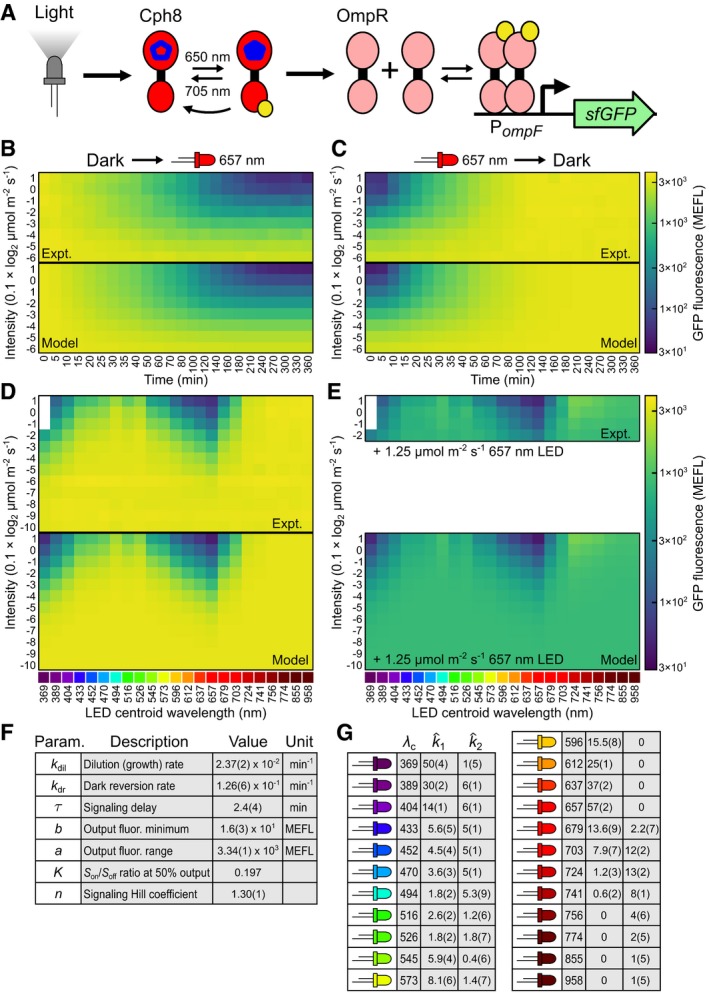
A-G.Caratterizzazione Cph8-OmpR e parametrizzazione del modello
I dettagli della A-GFigure sono descritti nella Fig. 2, e i datisono disponibili nel Dataset EV7. Si noti che le misure dello spettro ad azione inversa (E) contengono solo quattro intensità dei LED spettrali piuttosto che l’insieme completo dei 12 usati negli esperimenti CcaSR.I dettagli della figura sono descritti nella Fig. 2, edi dati sono disponibili nel Dataset EV7 . Si noti che le misure dello spettro ad azione inversa (E) contengono solo quattro intensità dei LED spettrali piuttosto che l’insieme completo dei 12 usati negli esperimenti CcaSR.
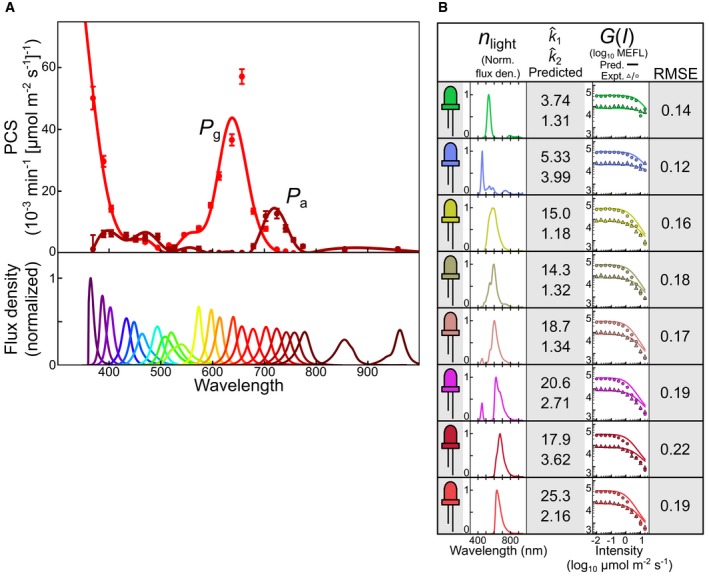
A, B.Stima Cph8 PCS e validazione spettrale del modello Cph8-OmpR
A, BFigure dettagli sono descritti nella Fig. 3, ei dati sono disponibili nel Dataset EV7 .I dettagli della figura sono descritti nella Fig 3, ei dati sono disponibili nel Dataset EV7 .
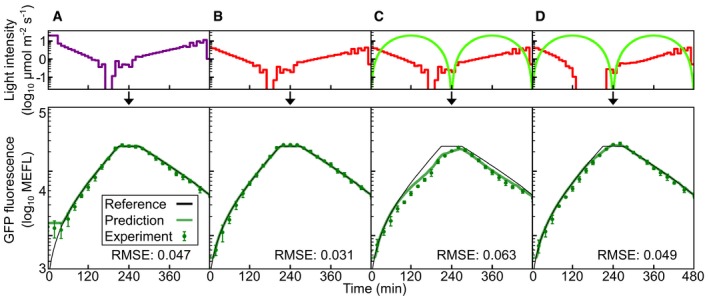
A-D.Convalida della programmazione dinamica del modello Cph8-OmpR
I dettagli delle cifre A-DFigure sono descritti nella Fig. 4, e i datisono disponibili nel Dataset EV7.I dettagli della figura sono descritti nella Fig 4, ei dati sono disponibili nel Dataset EV7 .

A-G.Caratterizzazione Cph8-OmpR e parametrizzazione del modello
I dettagli della A-GFigure sono descritti nella Fig. 2, e i datisono disponibili nel Dataset EV7. Si noti che le misure dello spettro ad azione inversa (E) contengono solo quattro intensità dei LED spettrali piuttosto che l’insieme completo dei 12 usati negli esperimenti CcaSR.I dettagli della figura sono descritti nella Fig. 2, edi dati sono disponibili nel Dataset EV7 . Si noti che le misure dello spettro ad azione inversa (E) contengono solo quattro intensità dei LED spettrali piuttosto che l’insieme completo dei 12 usati negli esperimenti CcaSR.

A, B.Stima Cph8 PCS e validazione spettrale del modello Cph8-OmpR
A, BFigure dettagli sono descritti nella Fig. 3, ei dati sono disponibili nel Dataset EV7 .I dettagli della figura sono descritti nella Fig 3, ei dati sono disponibili nel Dataset EV7 .

A-D.Convalida della programmazione dinamica del modello Cph8-OmpR
I dettagli delle cifre A-DFigure sono descritti nella Fig. 4, e i datisono disponibili nel Dataset EV7.I dettagli della figura sono descritti nella Fig 4, ei dati sono disponibili nel Dataset EV7 .
Sviluppo di un modello a doppio sistema CcaSR, Cph8-OmpR
Abbiamo progettato un sistema a tre plasmidi (Fig EV1 eDataset EV1) per esprimere CcaSR e Cph8-OmpR nella stessa cella con uscite sfGFP e mCherry, rispettivamente (Fig 5A). Per ricalibrare per mCherry [quantificato in Molecole di Cy5 equivalente (MECY)] ed eventuali cambiamenti dovuti al nuovo contesto cellulare, abbiamo misurato i livelli di stato stazionario di sfGFP e mCherry a diverse combinazioni di verde (λc= 526) e rosso (λc= 657) luce (Fig 5B, Appendice Fig S12 , e Dataset EV8) e riadattare i parametri della funzione Hill della porzione di segnalazione TCS del modello di uscita (Tabella EV6). Poiché i parametri di fotoconversione sono proprietà dei fotorecettori stessi, li abbiamo lasciati invariati. Il modello a doppio sistema cattura accuratamente le osservazioni sperimentali dal set di dati di caratterizzazione (Fig 5B).
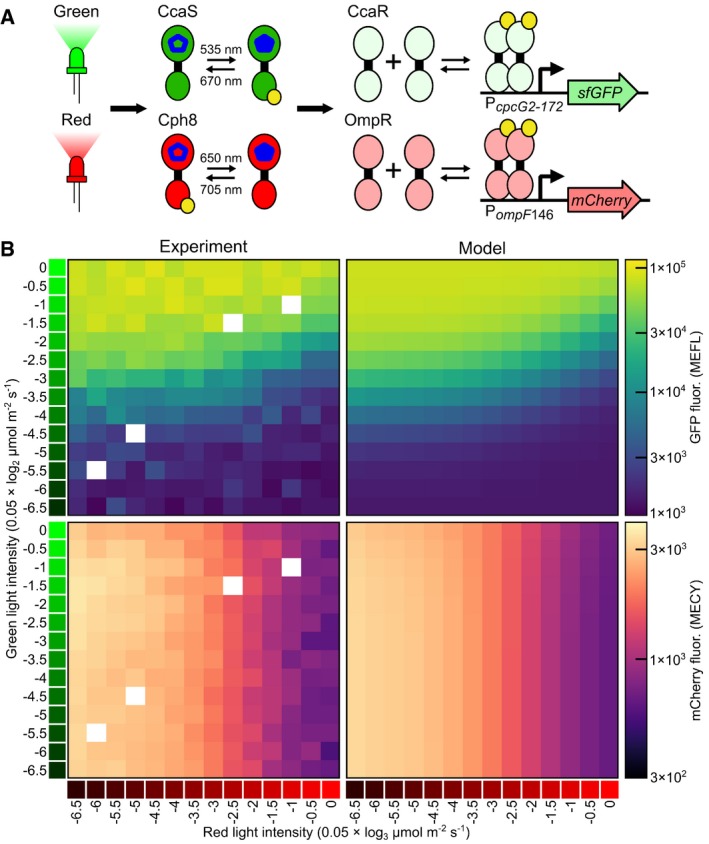
Figura 5.Caratterizzazione e modellazione di un sistema CcaSR/Cph8-OmpR multiplexato
CcaSR e Cph8-OmpR sono coespresse in una singola deformazione. CcaSR regola l’espressione di sfGFP, mentre Cph8-OmpR regola l’espressione di mCherry. I valori di lunghezza d’onda sono come in Fig 2A.I dati di addestramento per il modello multiplexato (“Experiment”, Dataset EV8) sono costituiti da una dose-risposta bidimensionale di intensità allo stato stazionario a due dimensioni (λc= 526 nm) e rosso (λc= 657 nm) luce. Le intensità della luce sono logaritmicamente distribuite, con la luce verde che varia su una scala di 0,05 × log2 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 2-1 = 10 μmol m-2 s-1) e la luce rossa varia su una scala di 0,05 × log3 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 3-1 = 6,67 μmol m-2 s-1). I diversi intervalli di intensità sono utilizzati per mantenere una misura ad alta risoluzione nonostante le differenze nelle dosi di intensità dei due sistemi. I quattro valori di intensità mancanti (scatole bianche) non sono stati raccolti. I dati di formazione sono stati utilizzati per riadattare i parametri di funzione a, b , n e K Hill per i modelli CcaSR e Cph8-OmpR (Tabella EV6).Sono mostrate risposte simulate allo stato stazionario agli stessi ambienti luminosi per i modelli a doppio sistema più adatti (Tabella EV6)(“Modello”). La fluorescenza mCherry è calibrata su unità MECY (Molecole di Cy5 equivalente, Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti in uno studio sperimentale e i 192 campioni sono stati distribuiti in modo casuale su otto LPA(Materiali e Metodi, Tabella EV6, e Dataset EV8). Ogni patch di colore rappresenta la media aritmetica di una singola popolazione di cellule.CcaSR e Cph8-OmpR sono coespresse in un unico ceppo. CcaSR regola l’espressione di sfGFP, mentre Cph8-OmpR regola l’espressione di mCherry. I valori della lunghezza d’onda sono come in Fig 2A.I dati di formazione per il modello multiplexato (“Esperimento”, Dataset EV8) consiste in una dose-risposta bidimensionale di intensità dello stato stazionario a verde (λc= 526 nm) e rosso (λc= 657 nm) luce. Le intensità della luce sono logaritmicamente distribuite, con la luce verde che varia su una scala di 0,05 × log2 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 2-1 = 10 μmol m-2 s-1) e la luce rossa varia su una scala di 0,05 × log3 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 3-1 = 6,67 μmol m-2 s-1). I diversi intervalli di intensità sono utilizzati per mantenere una misura ad alta risoluzione nonostante le differenze nelle dosi di intensità dei due sistemi. I quattro valori di intensità mancanti (scatole bianche) non sono stati raccolti. I dati di formazione sono stati utilizzati per riadattare i parametri di funzione a, b , n e K Hill per i modelli CcaSR e Cph8-OmpR (Tabella EV6).Sono mostrate risposte simulate allo stato stazionario agli stessi ambienti luminosi per i modelli a doppio sistema più adatti (Tabella EV6)(“Modello”). La fluorescenza mCherry è calibrata su unità MECY (Molecole di Cy5 equivalente, Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti in uno studio sperimentale e i 192 campioni sono stati distribuiti in modo casuale su otto LPA(Materiali e Metodi, Tabella EV6, e Dataset EV8). Ogni patch di colore rappresenta la media aritmetica di una singola popolazione di cellule.
Per convalidare il modello a doppio sistema, abbiamo utilizzato nuovamente l’approccio del generatore di funzioni biologiche (Fig 6 e Dataset EV8). Abbiamo progettato una serie di quattro programmi di espressione dual sfGFP/mCherry per sfidare sempre più il modello: “Green mono” utilizzando solo luce verde e destinato solo a controllare CcaSR (Fig 6A), “Red mono” utilizzando solo luce rossa e destinato solo a controllare Cph8-OmpR (Fig 6B), “Sum”., una semplice combinazione dei primi due programmi (Fig 6C), e “Somma compensata” dove il percorso temporale a luce verde viene ri-ottimizzato per tener conto della presenza del segnale rosso (Fig 6D) come prima (Materiali e metodi). A causa della risposta minima del doppio sistema Cph8-OmpR alla luce verde (Fig 5B), non èstatonecessario regolare il programma rosso per compensare la presenza della luce verde. I risultati sperimentali della validazione (Fig 6) mostrano che il nostro modello a doppio sistema cattura accuratamente sia le dinamiche di espressione sfGFP che mCherry. Le previsioni CcaSR sono quasi accurate come gli esperimenti su un singolo sistema (Fig 4), e i risultati Cph8-OmpR corrispondono all’accuratezza di un singolo sistema (Fig EV4), dimostrandol’estensibilità del nostro approccio agli strumenti optogenetici multipli.
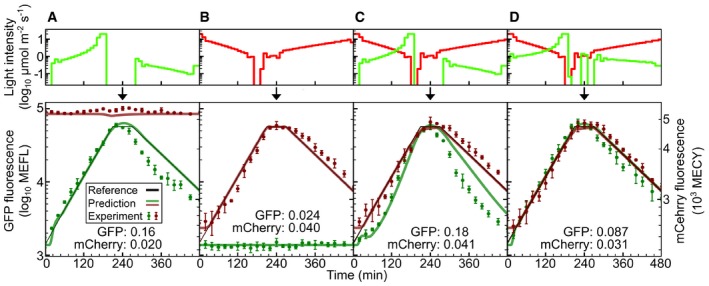
Figura 6.Convalida del modello di sistema multiplexatoRisposte previste del sistema multiplexato (Fig 5A)aisegnali variabili nel tempo di verde (λc= 526 nm) e rosso (λc= 657 nm) luce sono confrontati con i risultati sperimentali. I segnali di riferimento, i programmi di luce ed i dati sperimentali sono come in Fig 4.
4. “Mono verde”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato per la CcaSR. “Red mono”. Il LED rosso da solo fornisce un ingresso ottimizzato per Cph8-OmpR. “Sum”. I programmi “Green mono” e “Red mono” sono usati simultaneamente senza alcuna compensazione, portando ad una sostanziale deviazione dell’uscita CcaSR dalla traiettoria di riferimento. “Somma compensata”. Viene utilizzato il programma “Red mono”; tuttavia, il programma a luce verde viene prodotto mentre si incorpora il programma a luce rossa nel GPL (sopra): Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali separate(Tabella EV6 e Dataset EV8).“Mono verde”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato per la CcaSR.“Rosso mono”. Il LED rosso da solo fornisce un ingresso ottimizzato per Cph8-OmpR.“Somma”. I programmi “Green mono” e “Red mono” sono usati simultaneamente senza alcuna compensazione, portando ad una sostanziale deviazione dell’uscita CcaSR dalla traiettoria di riferimento.“Somma compensata”. Si usa il programma “Red mono”; tuttavia, il programma a luce verde viene prodotto mentre si incorpora il programma a luce rossa nel GPL (sopra).

Figura 5.Caratterizzazione e modellazione di un sistema CcaSR/Cph8-OmpR multiplexato
CcaSR e Cph8-OmpR sono coespresse in una singola deformazione. CcaSR regola l’espressione di sfGFP, mentre Cph8-OmpR regola l’espressione di mCherry. I valori di lunghezza d’onda sono come in Fig 2A.I dati di addestramento per il modello multiplexato (“Experiment”, Dataset EV8) sono costituiti da una dose-risposta bidimensionale di intensità allo stato stazionario a due dimensioni (λc= 526 nm) e rosso (λc= 657 nm) luce. Le intensità della luce sono logaritmicamente distribuite, con la luce verde che varia su una scala di 0,05 × log2 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 2-1 = 10 μmol m-2 s-1) e la luce rossa varia su una scala di 0,05 × log3 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 3-1 = 6,67 μmol m-2 s-1). I diversi intervalli di intensità sono utilizzati per mantenere una misura ad alta risoluzione nonostante le differenze nelle dosi di intensità dei due sistemi. I quattro valori di intensità mancanti (scatole bianche) non sono stati raccolti. I dati di formazione sono stati utilizzati per riadattare i parametri di funzione a, b , n e K Hill per i modelli CcaSR e Cph8-OmpR (Tabella EV6).Sono mostrate risposte simulate allo stato stazionario agli stessi ambienti luminosi per i modelli a doppio sistema più adatti (Tabella EV6)(“Modello”). La fluorescenza mCherry è calibrata su unità MECY (Molecole di Cy5 equivalente, Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti in uno studio sperimentale e i 192 campioni sono stati distribuiti in modo casuale su otto LPA(Materiali e Metodi, Tabella EV6, e Dataset EV8). Ogni patch di colore rappresenta la media aritmetica di una singola popolazione di cellule.CcaSR e Cph8-OmpR sono coespresse in un unico ceppo. CcaSR regola l’espressione di sfGFP, mentre Cph8-OmpR regola l’espressione di mCherry. I valori della lunghezza d’onda sono come in Fig 2A.I dati di formazione per il modello multiplexato (“Esperimento”, Dataset EV8) consiste in una dose-risposta bidimensionale di intensità dello stato stazionario a verde (λc= 526 nm) e rosso (λc= 657 nm) luce. Le intensità della luce sono logaritmicamente distribuite, con la luce verde che varia su una scala di 0,05 × log2 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 2-1 = 10 μmol m-2 s-1) e la luce rossa varia su una scala di 0,05 × log3 μmol m-2 s-1 (ad es, un valore di -1 corrisponde a 20 × 3-1 = 6,67 μmol m-2 s-1). I diversi intervalli di intensità sono utilizzati per mantenere una misura ad alta risoluzione nonostante le differenze nelle dosi di intensità dei due sistemi. I quattro valori di intensità mancanti (scatole bianche) non sono stati raccolti. I dati di formazione sono stati utilizzati per riadattare i parametri di funzione a, b , n e K Hill per i modelli CcaSR e Cph8-OmpR (Tabella EV6).Sono mostrate risposte simulate allo stato stazionario agli stessi ambienti luminosi per i modelli a doppio sistema più adatti (Tabella EV6)(“Modello”). La fluorescenza mCherry è calibrata su unità MECY (Molecole di Cy5 equivalente, Materiali e Metodi). Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). I dati sono stati raccolti in uno studio sperimentale e i 192 campioni sono stati distribuiti in modo casuale su otto LPA(Materiali e Metodi, Tabella EV6, e Dataset EV8). Ogni patch di colore rappresenta la media aritmetica di una singola popolazione di cellule.

Figura 6.Convalida del modello di sistema multiplexatoRisposte previste del sistema multiplexato (Fig 5A)aisegnali variabili nel tempo di verde (λc= 526 nm) e rosso (λc= 657 nm) luce sono confrontati con i risultati sperimentali. I segnali di riferimento, i programmi di luce ed i dati sperimentali sono come in Fig 4.
4. “Mono verde”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato per la CcaSR. “Red mono”. Il LED rosso da solo fornisce un ingresso ottimizzato per Cph8-OmpR. “Sum”. I programmi “Green mono” e “Red mono” sono usati simultaneamente senza alcuna compensazione, portando ad una sostanziale deviazione dell’uscita CcaSR dalla traiettoria di riferimento. “Somma compensata”. Viene utilizzato il programma “Red mono”; tuttavia, il programma a luce verde viene prodotto mentre si incorpora il programma a luce rossa nel GPL (sopra): Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali separate(Tabella EV6 e Dataset EV8).“Mono verde”. Il LED verde da solo fornisce un segnale di ingresso ottimizzato per la CcaSR.“Rosso mono”. Il LED rosso da solo fornisce un ingresso ottimizzato per Cph8-OmpR.“Somma”. I programmi “Green mono” e “Red mono” sono usati simultaneamente senza alcuna compensazione, portando ad una sostanziale deviazione dell’uscita CcaSR dalla traiettoria di riferimento.“Somma compensata”. Si usa il programma “Red mono”; tuttavia, il programma a luce verde viene prodotto mentre si incorpora il programma a luce rossa nel GPL (sopra).
Generazione di funzioni biologiche multiplexate
Infine, abbiamo progettato ed implementato sperimentalmente quattro funzioni di espressione multiplexate sfGFP/mCherry che rappresentano classi di segnali utili per la caratterizzazione dei circuiti genici(Dataset EV6 ed EV8). “Dual-sines” illustra che due sinusoidi di espressione genica con differenti offset, ampiezze e periodi possono essere composte senza interferenze (Fig 7A). Le variazioni di questa combinazione di segnali possono essere usate per eseguire l’analisi di frequenza di più nodi in una rete genica. “Seno e scale” dimostra che il nostro approccio può generare due segnali di espressione genica completamente diversi allo stesso tempo (Fig 7B). “Dual-stairs” dimostra che il rapporto di due proteine può essere variato su una gamma notevolmente ampia (Fig 7C). Infine, “Time-shifted waveform” (Fig 7D) dimostra che il nostro approccio può essere utilizzato per caratterizzare i circuiti genetici dove i ritardi sono critici, come quelli coinvolti nel processo decisionale cellulare.
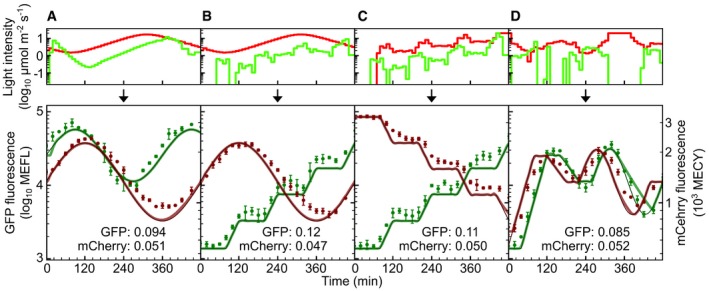
Figura 7.Generazione di funzioni biologiche multiplexateIl GPL è usato per programmare le uscite CcaSR e Cph8-OmpR per seguire indipendentemente i diversi segnali di riferimento. Luce rossa(λc= 657 nm) i programmi sono ottimizzati prima usando il GPL, e poi, l’approccio “Compensato” (Fig 6D) è utilizzato per generare la luce verde (λc= 526 nm) programma (Materiali eMetodi). “Dual-sines“. Le traiettorie di riferimento sfGFP e mCherry sono sinusoidi con diversi periodi, ampiezze e offset. “Seno e scale”. Il segnale mCherry segue la stessa sinusoide in “Dual-sines”, ma il riferimento sfGFP è una traiettoria a gradini con diversi piani e rampe lineari crescenti. “Dual-sscale”. Il segnale sfGFP segue la stessa forma d’onda a gradini in “Sine and stairs”; tuttavia, la risposta mCherry è una forma d’onda a gradini decrescente “Time-shifted waveform”. Le traiettorie di riferimento di sfGFP e mCherry seguono entrambe la stessa forma d’onda arbitraria composta da rampe, prese e una sinusoide, con sfGFP che trascina mCherry di 40 minuti: Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali indipendenti(Tabella EV6 e Dataset EV8).“Dual-sines”. Le traiettorie di riferimento sfGFP e mCherry sono sinusoidi con periodi, ampiezze e offset diversi.“Seno e scale”. Il segnale mCherry segue la stessa sinusoide in “Dual-sines”, ma il riferimento sfGFP è una traiettoria a gradini con diversi piani e rampe lineari crescenti.“Dual-stairs”. Il segnale sfGFP segue la stessa forma della scala in “Sine and stairs”; tuttavia, la risposta mCherry è una forma della scala decrescente.“Forma d’onda spostata nel tempo”. Le traiettorie di riferimento di sfGFP e mCherry seguono entrambe la stessa forma d’onda arbitraria composta da rampe, prese e una sinusoide, con sfGFP che traina mCherry di 40 min.

Figura 7.Generazione di funzioni biologiche multiplexateIl GPL è usato per programmare le uscite CcaSR e Cph8-OmpR per seguire indipendentemente i diversi segnali di riferimento. Luce rossa(λc= 657 nm) i programmi sono ottimizzati prima usando il GPL, e poi, l’approccio “Compensato” (Fig 6D) è utilizzato per generare la luce verde (λc= 526 nm) programma (Materiali eMetodi). “Dual-sines“. Le traiettorie di riferimento sfGFP e mCherry sono sinusoidi con diversi periodi, ampiezze e offset. “Seno e scale”. Il segnale mCherry segue la stessa sinusoide in “Dual-sines”, ma il riferimento sfGFP è una traiettoria a gradini con diversi piani e rampe lineari crescenti. “Dual-sscale”. Il segnale sfGFP segue la stessa forma d’onda a gradini in “Sine and stairs”; tuttavia, la risposta mCherry è una forma d’onda a gradini decrescente “Time-shifted waveform”. Le traiettorie di riferimento di sfGFP e mCherry seguono entrambe la stessa forma d’onda arbitraria composta da rampe, prese e una sinusoide, con sfGFP che trascina mCherry di 40 minuti: Gli errori relativi RMSE sono espressi in log10 decadi(Materiali e Metodi). Le barre di errore corrispondono alla deviazione standard nelle misure di fluorescenza su tre prove sperimentali indipendenti(Tabella EV6 e Dataset EV8).“Dual-sines”. Le traiettorie di riferimento sfGFP e mCherry sono sinusoidi con periodi, ampiezze e offset diversi.“Seno e scale”. Il segnale mCherry segue la stessa sinusoide in “Dual-sines”, ma il riferimento sfGFP è una traiettoria a gradini con diversi piani e rampe lineari crescenti.“Dual-stairs”. Il segnale sfGFP segue la stessa forma della scala in “Sine and stairs”; tuttavia, la risposta mCherry è una forma della scala decrescente.“Forma d’onda spostata nel tempo”. Le traiettorie di riferimento di sfGFP e mCherry seguono entrambe la stessa forma d’onda arbitraria composta da rampe, prese e una sinusoide, con sfGFP che traina mCherry di 40 min.
Discussione
Il nostro modello TCS optogenetico è superiore alle alternative attuali per diversi criteri chiave. In primo luogo, come la nostra versione precedente (Olson et al, 2014) , è quantitativamente predittivo e non richiede ricalibrazioni dei parametri da giorno a giorno. Tuttavia, mentre il modello precedente richiede una calibrazione sperimentale rispetto ad ogni sorgente luminosa utilizzata, quello attuale richiede solo un singolo set di esperimenti di calibrazione e poi si generalizza praticamente a qualsiasi sorgente luminosa o miscela di sorgenti luminose le cui caratteristiche spettrali possono essere misurate con uno spettroradiometro. In secondo luogo, il nostro modello optogenetico TCS è compatibile con fotorecettori con spettri di azione molto diversi, logica di segnalazione a terra opposta rispetto a quella a stato attivo, e tempi di inversione scuri drammaticamente diversi. In terzo luogo, il modello attuale disaccoppia modularmente i processi di rilevamento (fotoconversione) e di uscita (trasduzione del segnale ed espressione genica). La componente del modello di rilevamento (Fig 1A) dovrebbe essere compatibile con una vasta gamma di fotorecettori, compresi quelli di altri organismi, perché il meccanismo di fotoconversione a due stati del nucleo è usato per descrivere le loro prestazioni in vitro. Quindi, per descrivere gli strumenti optogenetici basati su questi fotorecettori, il nostro modello di uscita TCS può essere sostituito con alternative appropriate ad altri percorsi.
Uno dei principali problemi attuali dell’optogenetica è che gli strumenti sviluppati in diversi studi sono caratterizzati utilizzando diverse condizioni di coltura, esperimenti, fonti di luce, reporter, metriche e così via. Questa mancanza di standardizzazione rende difficile confrontare le caratteristiche prestazionali dei diversi strumenti optogenetici anche su base qualitativa. L’approccio di modellazione e caratterizzazione che sviluppiamo qui si basa su hardware ottico apertamente disponibile (Gerhardt et al, 2016) e sul software di analisi e calibrazione della citometria a flusso (Castillo-Hair et al, 2016). Così, i nostri risultati potrebbero essere direttamente riprodotti in altri laboratori utilizzando i programmi di luce qui riportati(Dataset EV2, EV7 ed EV8). Inoltre, il nostro approccio potrebbe essere utilizzato per realizzare schede tecniche che descrivono il comportamento di diversi strumenti optogenetici in unità standard. Questo vantaggio permetterebbe ai ricercatori di scegliere lo strumento più appropriato per le diverse applicazioni. Inoltre, si potrebbero identificare le carenze di strumenti specifici, informando gli sforzi per ottimizzare le prestazioni attraverso approcci razionali come il design delle proteine (McIsaac et al, 2014; Engqvist et al , 2015; Guntas et al, 2015 ).
Il nostro approccio dovrebbe consentire un migliore controllo degli strumenti optogenetici con hardware ottico alternativo o altamente limitato utilizzato in molti laboratori di ricerca. Ad esempio, molti gruppi eseguono studi optogenetici monocellulari utilizzando microscopi a fluorescenza con configurazioni ottiche fortemente limitate. In alternativa, i proiettori di consumo o i display dei tablet sono opzioni hardware potenzialmente potenti e a basso costo per l’optogenetica (Stirman et al, 2012; Beyer et al, 2015). Lo spettro di uscita della sorgente luminosa può essere misurato e integrato nel nostro flusso di lavoro. Dopo una semplice ricalibrazione (ad esempio, Fig 5) per tener conto di eventuali cambiamenti dovuti al nuovo ambiente di crescita, si dovrebbe essere in grado di prevedere e controllare lo strumento optogenetico utilizzando la nuova sorgente luminosa.
Spesso, è auspicabile controllare contemporaneamente uno strumento optogenetico mentre si esegue l’imaging di una cellula di interesse utilizzando fonti di luce bianca e luce di eccitazione per i reporter fluorescenti. Tali fonti di illuminazione alternative possono avere effetti deleteri sulla capacità di controllare lo strumento optogenetico. Tuttavia, se la natura del segnale di luce alternativa è nota, il nostro approccio può compensare tali perturbazioni (ad esempio, figg. 6 e 7). Nel controllo del feedback in silico è stato utilizzato anche per guidare le dinamiche di espressione genica desiderate negli esperimenti optogenetici (Milias-Argeitis et al, 2011, 2016 ; Melendez et al, 2014). Il principale vantaggio di questo approccio è che le perturbazioni di origine sconosciuta possono essere compensate monitorando le deviazioni nell’output di uno strumento optogenetico rispetto a un riferimento. Il nostro modello è compatibile con tali metodi di controllo del feedback in silico.
Mentre il controllo multicromatico di base degli strumenti optogenetici è stato precedentemente dimostrato (Tabor et al, 2011; Müller et al, 2013), l’approccio di generazione di funzioni biologiche multiplexate qui dimostrato estende notevolmente le capacità di questi sistemi, consentendo l’implementazione di diverse classi di esperimenti. Abbiamo già dimostrato che le dinamiche di espressione dei fattori di trascrizione, così come le proteine fluorescenti, possono essere controllate con i nostri strumenti optogenetici (Olson et al, 2014) . In primo luogo, la risposta bidimensionale di un circuito genetico o di un percorso di segnalazione potrebbe essere rapidamente valutata con elevata riproducibilità e precisione. Ad esempio, si potrebbe mappare la risposta dei gate logici trascrizionali a due ingressi (Nielsen et al, 2016), che integrano i livelli di espressione di due diversi fattori di trascrizione variando in modo sistematico e indipendente i loro livelli di espressione mentre si misura l’output del gate con un gene reporter. Le dinamiche di tali gate sono altrimenti difficili da valutare e raramente caratterizzate (Olson & Tabor, 2014 ). In secondo luogo, la dinamica di ingresso/uscita di un circuito trascrizionale potrebbe essere caratterizzata in funzione dello stato del circuito stesso. Per esempio, si potrebbe valutare quanto bene un oscillatore trascrizionale sintetico possa essere trascinato (Stricker et al, 2008; Mondragón-Palomino et al, 2011) in funzione della forza di un nodo di retroazione. In questo caso, uno strumento optogenetico potrebbe essere utilizzato per il trascinamento, mentre il secondo è stato utilizzato per modificare il livello di espressione di un fattore di trascrizione del circuito che regola la forza di feedback. In terzo luogo, la trascrizione e la proteolisi (Fernandez-Rodriguez & Voigt, 2016) potevano essere controllate in modo indipendente con due diversi strumenti optogenetici per programmare in alternativa rapidi aumenti o diminuzioni del livello di espressione. Un tale approccio potrebbe accelerare i segnali di espressione genica che abbiamo generato in questo e nel nostro studio precedente (Olson et al, 2014) , consentendo la caratterizzazione della dinamica del circuito genico su tempi più rapidi. Infine, la generazione di funzioni biologiche multiplexate potrebbe essere utilizzata per valutare come la tempistica dell’espressione di due geni influisce sul processo decisionale cellulare (Kuchina et al, 2011; Vishnoi et al, 2013; Castillo-Hair et al, 2015). Ad esempio, nel Bacillus subtilis, i circuiti genici che regolano la sporulazione e la competenza competono attraverso una “razza molecolare” nei livelli dei corrispondenti regolatori master (Kuchina et al, 2011). Mettendoli sotto un controllo optogenetico indipendente, i mezzi con cui la loro dinamica impatta queste decisioni cellulari potrebbero essere valutati più facilmente e rigorosamente.
Materiali e metodi
Ceppi batterici
Tutti i sistemi utilizzano il ceppo ospite E. coli BW29655 (Zhou et al , 2003). Il ceppo del sistema CcaSR porta i plasmidi pSR43.6 e pSR58.6, che conferiscono rispettivamente resistenza alla spectinomicina e al cloramfenicolo (Schmidl et al, 2014) . Il ceppo del sistema Cph8-OmpR porta i plasmidi pSR33,4 (spectinomicina) e pSR59,4 (ampicillina) (Schmidl et al, 2014). Il ceppo del sistema a doppio sistema trasporta pSR58,6, pSR78 (spectinomicina) e pSR83 (ampicillina). Sono disponibili mappe e sequenze di plasmidi (Fig EV1e Dataset EV1).
Crescita batterica ed esposizione alla luce
I protocolli di coltura cellulare e di raccolta sono stati sviluppati per garantire un alto grado di precisione e di riproducibilità negli esperimenti sia dal pozzo a pozzo che dal giorno per giorno (Appendice MetodoS1). Le cellule sono state coltivate a 37°C e agitate a 250 rpm durante tutto l’esperimento (Sheldon Manufacturing Inc. SI9R) con temperatura calibrata e registrata mettendo una sonda termometrica in un pallone sigillato da 125 ml riempito d’acqua (Traceable Excursion-Trac 6433). Le colture sono state coltivate in mezzi M9 integrati con 0,2% di casaminoacidi, 0,4% di glucosio e antibiotici appropriati. Preculture sono state preparate in anticipo congelando 100-μl aliquote di 100-μl di colture in fase esponenziale precoce (OD600 =0,1-0,2) coltivate nelle stesse condizioni di media a -80 ° C (Appendice Metodo S2). Le colture sono state inoculate a basse densità (tipicamente OD600 = 1 × 10-5) per garantire che le densità finali non raggiungessero la fase stazionaria (OD600 < 0,2). Per ogni esperimento, 192 colture sono state coltivate in volumi di 500 μl all’interno di piastre a 24 pozzetti (ArcticWhite AWLS-303008), sigillate con pellicola adesiva (VWR 60941-126).
Sono stati effettuati esperimenti utilizzando otto strumenti LPA a 24 pozzetti (Gerhardt et al, 2016), che hanno permesso di controllare con precisione due LED per definire l’ambiente ottico di 192 culture alla volta. I file di programma LPA sono stati generati utilizzando Iris (Gerhardt et al, 2016) e uno strumento Python personalizzato (DatasetEV9).
Misurazione LED
Tutti i LED sono stati misurati e calibrati(Appendice Metodo S3 e Dataset EV3) utilizzando uno spettrometro (StellarNet UVN-SR-25 LT16) con calibrazioni di fabbrica tracciabili NIST eseguite su entrambi gli assi di lunghezza d’onda e intensità immediatamente prima dell’uso per questo studio. È stata utilizzata una sfera integratrice da sei pollici (StellarNet IS6) che consente di misurare la potenza totale in uscita di ogni LED (in μmol s-1). Lo spettrofotometro è stato oscurato dalla misurazione di un campione scuro prima di ogni misurazione del LED. Le misurazioni sono state salvate come file .IRR, che contengono la densità di potenza spettrale completa del LED Plight(λ ) (μmol s-1 nm-1) in incrementi di 0,5 nm, nonché tutti i parametri di impostazione per la misurazione (cioè, tempo di integrazione e numero di scansioni in media). Questi file sono stati elaborati da script Python per calcolare le caratteristiche dei LED, compresi il picco, il centroide, FWHM e la potenza totale. Per gli esperimenti di validazione spettrale, sono stati tagliati dei filtri di illuminazione cinematografica (Roscolux), formati in tappi a forma di LED, e sono stati montati dei LED bianchi in cima (Tabella EV1).
Calcolo della luce
Poiché i LED che utilizziamo hanno caratteristiche spettrali fisse, la densità di flusso spettrale (μmol m-2 s-1 nm-1) incidente sui fotorecettori può essere parametrizzata dall’intensità del LED (μmol m-2 s-1). Le colture sono scosse durante tutto l’esperimento, e si suppone che le cellule siano ben miscelate all’interno del volume della coltura. Così, l’intensità media della luce all’interno del volume della coltura, leggera(λ ), può essere calcolata integrando l’intensità in tutto il volume del pozzo. Sotto l’ipotesi di assorbimento della luce trascurabile da parte del campione di coltura (il media M9 è trasparente, e le colture sono raccolte a bassa densità), questo integrale semplifica per diventare la potenza totale del LED (μmol s-1) diviso per la sezione trasversale del pozzo. Dato un raggio del pozzo di 7,5 mm, si calculatenlightλ=Plightλπ7.5×10-3m2≈5.659×103m-2×Plightλ
Calibrazione LED
Ognuno dei circa 700 singoli LED utilizzati nello studio è stato misurato(Appendice Metodo S3 e Dataset EV3), consentendo la compensazione della variazione nella produzione di LED e LPA (Tabelle EV1, EV2 e EV3 e Dataset EV9). Ogni LED è stato calibrato mentre era alimentato dalla stessa presa LPA utilizzata negli esperimenti. In primo luogo, è stato misurato un campione di LED per identificare la corrente elettrica necessaria a raggiungere un adeguato livello di flusso totale, ∫nlightλdλ. La quantità di corrente richiesta variava a seconda della lunghezza d’onda e del produttore. La corrente è stata regolata utilizzando il “dot-correction (DC)” LPA per ottenere un flusso totale di circa il 20% superiore a 20 μmol m-2 s-1 quando il LED era completamente illuminato. Per ogni modello di LED è stato determinato il livello di corrente continua appropriato. Utilizzando questi livelli DC, è stato misurato il set completo di LED. I LED che producevano un flusso totale inferiore a 20 μmol m-2 s-1 sono stati rimisurati ad un livello di corrente continua superiore. Questa serie di misurazioni dei LED è stata utilizzata per convertire l’andamento temporale dell’intensità desiderata di ogni LED in una serie di valori di scala di grigi a 12 bit (cioè 0-4.095) utilizzati dall’LPA. L’LPA legge i valori della scala di grigi per produrre l’appropriato segnale modulato in larghezza di impulso (PWM) per ottenere le intensità desiderate.
Raccolta di campioni batterici
Le colture sono state raccolte per la misurazione(Appendice Metodo S1) dopo una crescita di 8 ore precise, mettendo le piastre a 24 pozzetti in bagni di acqua ghiacciata. Ogni coltura è stata poi sottoposta sia ad una misura di assorbanza per garantire una crescita costante da pozzo a pozzo e giornaliera, sia alla citometria a flusso per la quantificazione dell’espressione di sfGFP o mCherry. Le misure di assorbanza sono state eseguite in piastre a 96 pozzetti a parete nera con fondo trasparente (VWR 82050-748) in un lettore di piastre (Tecan Infinite M200 Pro). Prima di eseguire le misurazioni di fluorescenza, i campioni di coltura sono stati processati attraverso un protocollo di maturazione di fluorescenza per garantire che le misurazioni fossero rappresentative della quantità totale di reporter fluorescente prodotto (Olson et al, 2014) . La rifampicina (Tokyo Chemical Industry R0079) è stata disciolta in soluzione salina tamponata con fosfato (PBS, VWR 72060-035) a 500 μg/ml e utilizzata per inibire la produzione di sfGFP durante la maturazione.
Citometria a flusso
Le distribuzioni di fluorescenza della popolazione sono state misurate per ogni coltura su un citometro a flusso come descritto in precedenza (Olson et al, 2014) . Un campione di microsfere di calibrazione (Spherotech RCP-30-5A) in PBS è stato misurato immediatamente prima dei campioni di coltura di ogni prova sperimentale. Sono stati raccolti almeno 5.000 eventi per il campione di microsfere di calibrazione e almeno 20.000 eventi per ogni campione di coltura.
Analisi dei dati di citometria a flusso
Le distribuzioni monocellulari di fluorescenza sfGFP sono state gated, analizzate e calibrate in unità MEFL e MECY utilizzando FlowCal (Castillo-Hair et al, 2016) tramite uno script Python personalizzato (Dataset EV9). Le misurazioni sono state gated sui canali FSC e SSC utilizzando una frazione di gate di 0,3 per le perline di calibrazione e 0,8 per i campioni cellulari (Castillo-Hair et al, 2016). I valori di fluorescenza di coltura riportati sono i mezzi aritmetici delle popolazioni cellulari.
Modello di rilevamento
Il modello di rilevamento della luce può essere descritto dal seguente sistema di ODE:
dSgdt=kS+kS+k2+kdr-Sat-k1+kdil-SgtdSadt=k1-Sgt-k2+kdil+kdr-Sat,
dove le variabili e i tassi sono stati precedentemente introdotti(Introduzione, Risultati) con i valori di best-fit riassunti nelle Figg. 2F e EV2F. Si noti che k1e k2sono implicitamente dipendenti dal tempo, in quanto sono funzioni dell’ambiente luminoso variabile nel tempo dei sensori.
Se si sostituisce la frazione di sensori attivi, y≡Sa/(Sg+Sa), il sistema pu` o essere espresso come:
dydt=k1-k1-k1+k2+kdil+kdr-yt=k1-ktot-yt,
dove ktot≡k1+k2+kdil+kdr.
Questo ODE può essere risolto analiticamente per un passaggio di luce da un ambiente all’altro. Se il cambiamento a gradino avviene al tempo t = 0, allora k1, k2e ktot sonotutti fissi per t > 0. Data una frazione inizialedel sensore y(0) = y0, troviamo.
yt=y0+k1ktot-y0-1-e-ktott.
Questa soluzione rappresenta una transizione esponenziale da una frazione iniziale del sensore di y0ad una frazione finale data da k1/ktot con una costante di tempo impostata da ktot. Di conseguenza, si prevede che la dinamica di transizione di y(t) sarà più lenta sotto illuminazione zero quando ktot= kdil + kdr. Ci aspettiamo anche che i tassi di transizione non siano limitati all’aumentare dell’intensità.
Infine, per sorgenti luminose multiple, combiniamo semplicemente linearmente i tassi di fotoconversione di ciascuna sorgente:ki= kiFonte 1+ kiFonte 2.
Modello di segnalazione TCS
Utilizziamo un modello altamente semplificato di segnalazione TCS e di regolazione dei geni. Questo modello mette in relazione il tasso di produzione del gene di uscita kG(t) al rapporto attivo dei sensori di luce SatSgt=yt1-yt≡Rt. Modelliamo la segnalazione TCS come un puro ritardo temporale τ e una funzione sigmoidale Hill. Per CcaSR, la funzione Hill viene attivata aumentando i rapporti dei sensori, mentre per Cph8-OmpR, l’attività di segnalazione TCS invertita si traduce in una funzione Hill repressa. Così, scriviamo kGt=b^+a^Rt-τnKn+Rt-τn per CcaSR e kGt=b^+a^KnKn+Rt-τn per Cph8-OmpR, dove le variabili e i tassi sono stati precedentemente introdotti (Introduzione, Risultati)con i valoribest-fit riassunti nelle Figg. 2F e EV2F.
Modello di espressione genica in uscita
Modelliamo l’espressione del gene di uscita in base alla produzione del primo ordine e alle dinamiche di diluizione: dGdt=kG(t)-kdil-Gt,
dove le variabili e i tassi sono stati precedentemente introdotti(Introduzione, Risultati) con i valori di best-fit riassunti nelle Figg. 2F e EV2F.
Generazione di simulazioni di modelli
Le simulazioni(Dataset EV2, EV7 ed EV8) sono state prodotte integrando numericamente il sistema di ODE con il metodo scipy.integrate.ode di Python utilizzando l’integratore “zvode” con un massimo di 3.000 passi (DatasetEV4).
Parametrizzazione del modello
I modelli CcaSR e Cph8-OmpR sono stati parametrizzati usando l’adattamento globale dei parametri del modello ai set di dati completi di addestramento (Figg. 2B-EedEV2B-E, e i set di dati EV2 ed EV7). Il pacchetto “lmfit” Python, che si basa sull’algoritmo di minimizzazione di Levenberg-Marquardt, è stato utilizzato per eseguire gli adattamenti e analizzare i set di parametri risultanti (Newville et al, 2014) . Gli adattamenti sono stati eseguiti minimizzando la somma del quadrato dell’errore relativo tra ogni punto di dati misurati e lo stesso punto in una simulazione di modello corrispondente. Così, la forma dell’errore metrico utilizzato è stato l’errore=∑iGidata-GimodelGidata2 attraverso l’insieme completo dei punti di dati {Gidata}.
Stima dei PCS
Le stime della sezione d’urto della fotoconversione σiest.(λ) sono state costruite facendo regredire linearmente una spline cubica ai tassi di fotoconversione determinati sperimentalmente per produrre un PCS continuo (AppendiceFig S5 e Dataset EV5 ). I σiest.(λ) sono stati prodotti minimizzando l’errore tra le velocità di fotoconversione sperimentali unitarie k^iexpt. (Figs 2FeEV2F) e le previsioni derivate da spline k^ipred.=∫σiest.-n^lightdλ. Le spline sono state costruite stabilendo una serie di vincoli integrali per i tassi di fotoconversione, vincoli di continuità per i nodi della spline e vincoli di confine. Poiché questo problema contiene più vincoli che parametri, è necessaria un’ottimizzazione. Per ottimizzare ogni spline, abbiamo usato i minimi quadrati ponderati con i moltiplicatori Lagrange. Per evitare la sovraparametrizzazione del σiest.(λ), abbiamo usato “Leave-one-out cross-validation (LOOCV)” per valutare le prestazioni delle spline con un numero di nodi compreso tra 5 e 20 per determinare il numero ideale richiesto per ogni The σiest.(λ) (Appendice Fig S6). Il numero ottimale di spline risultante è stato di 12 e 8 per CcaS σg e σa e 12 e 12 per Cph8 σg e σa. Un nodo è stato fissato a 1.050 nm, e i nodi rimanenti sono stati distribuiti uniformemente tra 350 e 800 nm (AppendiceFigg. S5 e S6).
Calcolo dell’errore di previsione (RMSE)
Per la validazione del modello, usiamo una metrica di errore relativo (RMSE=(∑ilog10(Gi(pred.)/Gi(expt.)))2/n) che riporta l’errore radice-media-quadrato (RMS) del log10 tra le risposte previste e quelle misurate (Set di datiEV2, EV7 ed EV8 ).
Algoritmo del generatore di programmi di luce (GPL)
Il GPL è stato utilizzato come descritto in precedenza (Olson et al, 2014) . L’unica modifica è stata quella di utilizzare le simulazioni generate dal modello qui descritto piuttosto che dal modello precedente. I programmi di luce compensata sono stati generati incorporando la presenza del segnale luminoso esterno nelle simulazioni del modello.
Confronto delle gamme di espressione del gene di uscita per i sistemi a singolo o a doppio sistema
Il range di uscita CcaSR è quasi conservato (60 volte contro 56 volte), mentre la risposta mCherry da Cph8-OmpR è sostanzialmente ridotta (210 volte contro 6,0 volte). Inoltre, la risposta alla luce è meno sensibile di quella osservata per Cph8-OmpR singolarmente, in quanto la mezza compressione richiede un’intensità 5,2 volte maggiore (Appendice FigS14). Si ipotizza che la riduzione del range di uscita e la diminuzione della sensibilità del Cph8-OmpR derivi da una competizione tra Cph8 e CcaS per la limitazione del PCB, che porta ad una sostanziale popolazione di apo-Cph8 insensibile alla luce. In particolare, il tasso di crescita(Appendice Fig S13) del ceppo a doppio sistema (39,2 min per raddoppio) è solo marginalmente più lento dei ceppi a sistema singolo (37,4 e 37,9 min per CcaSR e Cph8-OmpR, rispettivamente).
Descrizioni dettagliate dei segnali di riferimento della generazione di funzioni multiplexate
Nelle descrizioni seguenti dei segnali di riferimento della generazione di funzioni multiplexate(Dataset EV8), le percentuali e le frazioni corrispondono ad una rappresentazione su scala log del campo di uscita (ad esempio, se un sistema ha un campo di uscita di 16 volte, il livello del 50% su una scala log sarebbe alla stessa espressione al livello del 25% su una scala lineare).
Duplice linea. Il segnale di riferimento mCherry è descritto dalla funzione 0.5+0.3sin(2πt/480min) mentre il segnale di riferimento sfGFP segue 0.7+0.2sin(2πt/360min).seno e passi. Il segnale di riferimento mCherry è lo stesso che in “Dual-sines”, mentre il segnale sfGFP è una serie di hold di 80 minuti e rampe lineari di 40 minuti in incrementi crescenti del 20% del campo di uscita.Il segnale sfGFP è lo stesso del programma “Sine and steps”, mentre il segnale mCherry è l’inverso dello stesso programma. (Time-shifted waveform). Il segnale mCherry è una funzione complessa che consiste nei seguenti passi: rampa lineare da 0 a 70% su 80 min,mantenimento al 70% per 40 min,rampa lineare fino al 50% su 60 min,mantenimento al 50% per 40 min,segnale sinusoidale descritto dalla funzione 0.5+0.25sin(2πt-220min/220min),mantenimento al 50% per 40 min.
Il segnale sfGFP è lo stesso programma ma ritardato di 60 min.
Contributi dell’autore
EJO e JJT hanno concepito il progetto. EJO ha progettato ed eseguito esperimenti ed ha analizzato i dati. CNT ha assistito la costruzione delle stime della sezione trasversale di fotoconversione e la progettazione/prestazione delle prove di convalida spettrale. EJO e JJT hanno scritto il manoscritto.
Conflitto di interessi
Gli autori dichiarano di non avere alcun conflitto di interessi.
Informazioni di supporto
References
- Red light‐regulated reversible nuclear localization of proteins in mammalian cells and Zebrafish. ACS Synth Biol. 2015; 4:951-958. PubMed
- Actton spectra of phytochrome in vitro. Photochem Photobiol. 1964; 3:521-528.
- How to train your microbe: methods for dynamically characterizing gene networks. Curr Opin Microbiol. 2015; 24:113-123. PubMed
- FlowCal: a user‐friendly, open source software tool for automatically converting flow cytometry data from arbitrary to calibrated units. ACS Synth Biol. 2016; 5:774-780. PubMed
- Directed evolution of gloeobacter violaceus rhodopsin spectral properties. J Mol Biol. 2015; 427:205-220. PubMed
- Post‐translational control of genetic circuits using Potyvirus proteases. Nucleic Acids Res. 2016; 44:6493-6502. PubMed
- An open‐hardware platform for optogenetics and photobiology. Sci Rep. 2016; 6:35363. PubMed
- Characterization of bacteriophytochromes from photosynthetic bacteria: histidine kinase signaling triggered by light and redox sensing. Methods Enzymol. 2010; 471:135-159. PubMed
- Engineering an improved light‐induced dimer (iLID) for controlling the localization and activity of signaling proteins. Proc Natl Acad Sci USA. 2015; 112:112-117. PubMed
- Cyanobacteriochrome CcaS is the green light receptor that induces the expression of phycobilisome linker protein. Proc Natl Acad Sci USA. 2008; 105:9528-9533. PubMed
- A singular bacteriophytochrome acquired by lateral gene transfer. J Biol Chem. 2007; 282:7320-7328. PubMed
- Temporal competition between differentiation programs determines cell fate choice. Mol Syst Biol. 2011; 7:557. PubMed
- Synthetic biology: engineering Escherichia coli to see light. Nature. 2005; 438:441-442. PubMed
- Photoexcited CRY2 interacts with CIB1 to regulate transcription and floral initiation in Arabidopsis. Science. 2008; 322:1535-1539. PubMed
- Directed evolution of a far‐red fluorescent rhodopsin. Proc Natl Acad Sci USA. 2014; 111:13034-13039. PubMed
- Real‐time optogenetic control of intracellular protein concentration in microbial cell cultures. Integr Biol (Camb). 2014; 6:366-372. PubMed
- In silico feedback for in vivo regulation of a gene expression circuit. Nat Biotechnol. 2011; 29:1114-1116. PubMed
- Automated optogenetic feedback control for precise and robust regulation of gene expression and cell growth. Nat Commun. 2016; 7:12546. PubMed
- Structure and function of plant photoreceptors. Annu Rev Plant Biol. 2010; 61:21-47. PubMed
- Entrainment of a population of synthetic genetic oscillators. Science. 2011; 333:1315-1319. PubMed
- Multi‐chromatic control of mammalian gene expression and signaling. Nucleic Acids Res. 2013; 41:e124. PubMed
- LMFIT: non‐linear least‐square minimization and curve‐fitting for Python [Data set]. Zenodo.. 2014. Publisher Full Text
- Genetic circuit design automation. Science. 2016; 352:aac7341. PubMed
- Characterizing bacterial gene circuit dynamics with optically programmed gene expression signals. Nat Methods. 2014; 11:449-455. PubMed
- Optogenetic characterization methods overcome key challenges in synthetic and systems biology. Nat Chem Biol. 2014; 10:502-511. PubMed
- Phytochrome structure and signaling mechanisms. Annu Rev Plant Biol. 2006; 57:837-858. PubMed
- A brief history of phytochromes. Chemphyschem. 2010; 11:1172-1180. PubMed
- Red/green cyanobacteriochromes: sensors of color and power. Biochemistry. 2012; 51:9667-9677. PubMed
- Photosynthetic efficiency and phytochrome photoequilibria determination using spectral data. Trans ASAE. 1988; 31:1882-1889.
- Refactoring and optimization of light‐switchable Escherichia coli two‐component systems. ACS Synth Biol. 2014; 3:820-831. PubMed
- A multispectral optical illumination system with precise spatiotemporal control for the manipulation of optogenetic reagents. Nat Protoc. 2012; 7:207-220. PubMed
- A fast, robust and tunable synthetic gene oscillator. Nature. 2008; 456:516-519. PubMed
- The photocycle of a flavin‐binding domain of the blue light photoreceptor phototropin. J Biol Chem. 2001; 276:36493-36500. PubMed
- Multichromatic control of gene expression in Escherichia coli. J Mol Biol. 2011; 405:315-324. PubMed
- Triggering sporulation in Bacillus subtilis with artificial two‐component systems reveals the importance of proper Spo0A activation dynamics. Mol Microbiol. 2013; 90:181-194. PubMed
- Phenotype microarray analysis of Escherichia coli K‐12 mutants with deletions of all two‐component systems. J Bacteriol. 2003; 185:4956-4972. PubMed
Fonte
Olson EJ, Tzouanas CN, Tabor JJ (2017) A photoconversion model for full spectral programming and multiplexing of optogenetic systems. Molecular Systems Biology 13(4): 926. https://doi.org/10.15252/msb.20167456





