Abstract
Introduzione
L’apprendimento in due fasi è stato descritto in una varietà di contesti e circuiti neurali diversi. Durante il consolidamento della memoria ippocampale, le memorie recenti, che dipendono dall’ippocampo, vengono trasferite alla neocorteccia per la conservazione a lungo termine(Frankland e Bontempi, 2005). Allo stesso modo, la corteccia motoria di ratto fornisce l’input essenziale ai circuiti sub-corticali durante l’apprendimento delle abilità, ma diventa poi dispensabile per l’esecuzione di alcune abilità(Kawai et al., 2015). Un esempio paradigmatico di apprendimento in due fasi è rappresentato dagli uccelli canori che imparano le canzoni di corteggiamento(Andalman e Fee, 2009; Turner e Desmurget, 2010; Warren et al., 2011). I fringuelli della zebra, comunemente usati nella ricerca sul canto degli uccelli, imparano il loro canto dai loro padri da giovani e conservano lo stesso canto per tutta la vita(Immelmann, 1969).
Il circuito del canto degli uccelli è stato ampiamente studiato; si veda la Figura 1A per uno schema. L’area HVC è un circuito a base di tempo, con neuroni di proiezione che sparano spuntoni sparsi scoppiano in precisa sincronia con il canto(Hahnloser et al., 2002; Lynch et al., 2016; Picardo et al., 2016). Una popolazione di neuroni da HVC proietta al nucleo robusto dell’arcopallium (RA), un’area pre-motoria, che poi proietta ai motoneuroni che controllano i muscoli respiratori e siringhe(Leonardo e Fee, 2005; Simpson e Vicario, 1990; Yu e Margoliash, 1996). Un secondo input alla RA proviene dal nucleo magnocellulare laterale del nidopallio anteriore (LMAN). A differenza dei modelli di attività HVC e RA, il picco LMAN è altamente variabile attraverso diverse interpretazioni della canzone(Kao et al., 2008; Ölveczky et al., 2005). LMAN è l’uscita del percorso del proencefalo anteriore, un circuito che coinvolge i gangli basali specializzati nel canto(Perkel, 2004).10.7554/eLife.20944.002Figure 1.Relation between the song system in zebra finches and our model.(A) Diagramma delle principali regioni cerebrali coinvolte nel canto degli uccelli.(B) Modello concettuale ispirato al sistema del canto degli uccelli. La linea dall’uscita al tutor è tratteggiata perché il segnale di rinforzo può raggiungere il tutor sia direttamente che, come negli uccelli canori, indirettamente.(C) Regola di plasticità misurata in bird RA (misura fatta in fetta). Quando un burst HVC conduce un burst LMAN di circa 100ms, la sinapsi HVC-RA viene rinforzata, mentre la cottura coincidente porta alla soppressione. Figura adattata da Mehaffey e Doupe (2015).(D) Regola di plasticità nel nostro modello che imita la regola di Mehaffey e Doupe (2015).DOI:http://dx.doi.org/10.7554/eLife.20944.002
A causa della variabilità dei suoi modelli di attività, si è pensato che il ruolo di LMAN fosse semplicemente quello di iniettare variabilità nella canzone (Ölveczky et al., 2005). La sperimentazione vocale risultante avrebbe permesso un apprendimento basato sul rinforzo. Per questo motivo, i modelli precedenti tendevano a trattare LMAN come un puro generatore di rumore di Poisson, e presuppongono che un segnale di ricompensa venga ricevuto direttamente in RA(Fiete et al., 2007). Prove più recenti, tuttavia, suggeriscono che il segnale di ricompensa raggiunga l’Area X, i gangli basali specializzati in canti, piuttosto che l’RA(Gadagkar et al., 2016; Hoffmann et al., 2016; Kubikova et al., 2010). Considerato insieme al fatto che i modelli di sparo LMAN non sono uniformemente casuali, ma contengono piuttosto una distorsione correttiva che guida la plasticità della RA(Andalman and Fee, 2009; Warren et al., 2011), questo suggerisce che dovremmo ripensare i nostri modelli di acquisizione delle canzoni.
Qui costruiamo un modello generale di apprendimento in due fasi in cui un circuito neurale “tutorizza” un altro. Sviluppiamo un formalismo per determinare come il segnale didattico debba essere adattato a una specifica regola di plasticità, per istruire al meglio un circuito di studenti a migliorare le proprie prestazioni in ogni fase di apprendimento. Sviluppiamo risultati analitici in un modello basato sul tasso, e mostriamo attraverso simulazioni che i risultati generali portano a neuroni a picco realistici. Applicato al circuito di controllo vocale degli uccelli canori, il nostro modello riproduce i cambiamenti osservati nelle statistiche di picco dei neuroni RA mentre gli uccelli giovani imparano il loro canto. Il nostro modello prevede anche come il segnale LMAN debba essere adattato alle proprietà delle sinapsi RA. Questa previsione può essere testata in esperimenti futuri.
Il nostro approccio separa la questione meccanicistica di come viene attuato l’apprendimento da quelle che sono le regole di apprendimento che ne derivano. Dimostriamo tuttavia che un semplice algoritmo di apprendimento di rinforzo è sufficiente per implementare la regola di apprendimento da noi proposta. Il nostro quadro fa previsioni generali su come i segnali istruttivi sono abbinati alle regole di plasticità ogni volta che le informazioni vengono trasferite tra le diverse regioni cerebrali.
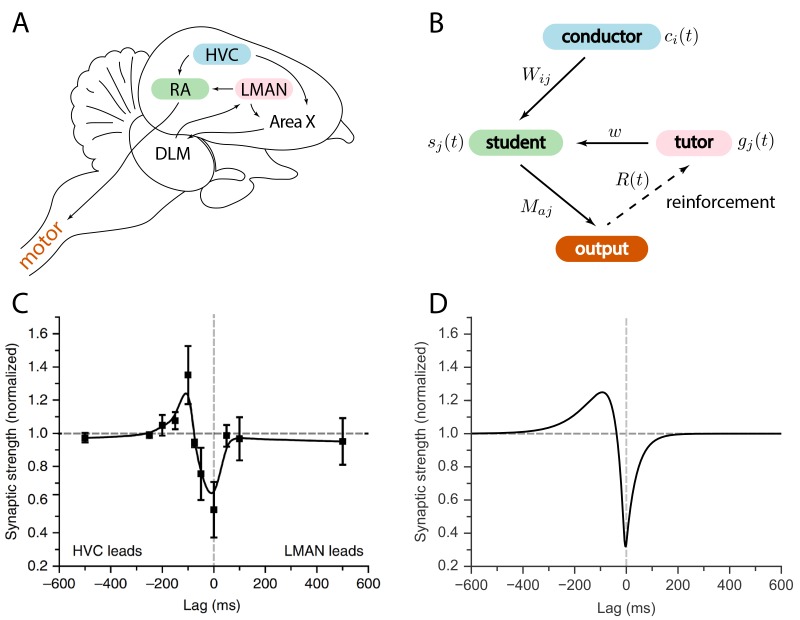
Figura 1.Relazione tra il sistema di canto nei fringuelli zebrati ed il nostro modello.(A) Diagramma delle principali regioni cerebrali coinvolte nel canto degli uccelli.(B) Modello concettuale ispirato al sistema del canto degli uccelli. La linea dall’uscita al tutor è tratteggiata perché il segnale di rinforzo può raggiungere il tutor sia direttamente che, come negli uccelli canori, indirettamente.(C) Regola di plasticità misurata in bird RA (misura fatta in fetta). Quando un burst HVC conduce un burst LMAN di circa 100ms, la sinapsi HVC-RA viene rinforzata, mentre la cottura coincidente porta alla soppressione. Figura adattata da Mehaffey e Doupe (2015).(D) Regola di plasticità nel nostro modello che imita la regola di Mehaffey e Doupe (2015).DOI:
http://dx.doi.org/10.7554/eLife.20944.002
Risultati
Modello
Abbiamo considerato un modello per il trasferimento di informazioni che è composto da tre sottocircuiti: un conduttore, uno studente e un tutor (vedi Figura 1B). Il conduttore fornisce input allo studente sotto forma di modelli temporalmente precisi. L’obiettivo dell’apprendimento è che lo studente converta questo input in un modello di output predefinito. Il tutor fornisce un segnale che guida la plasticità alle sinapsi conduttore-studente. Per semplicità, abbiamo supposto che il conduttore presenti sempre gli schemi di ingresso nello stesso ordine e senza ripetizioni. Questo ci ha permesso di utilizzare il tempo t per etichettare gli schemi di input, rendendo più facile l’analisi delle regole di apprendimento on-line che abbiamo studiato. Questo modello di apprendimento si basa sulla logica implementata dai circuiti vocali dell’uccello canterino(Figura 1A). In relazione al songbird, il conduttore è HVC, lo studente è RA e il tutor è LMAN. Il brano può essere visto come una mappatura tra i pattern di attività HVC simili ad un orologio e le uscite RA relative ai muscoli. L’obiettivo dell’apprendimento è quello di trovare una mappatura che riproduca la canzone del tutor.
Il canto degli uccelli fornisce interessanti intuizioni sul ruolo della variabilità nei segnali del tutor. Se ci concentriamo esclusivamente sul trasferimento di informazioni, l’uscita del tutor non deve necessariamente essere variabile; può fornire in modo deterministico il miglior segnale istruttivo per guidare lo studente. Questo, tuttavia, richiederebbe che il tutor abbia un modello dettagliato dello studente. Più realisticamente, il tutor potrebbe avere accesso solo ad una rappresentazione scalare di quanto sia riuscita la resa dello studente dell’output desiderato, magari sotto forma di segnale di ricompensa. In questo caso il tutor deve risolvere il cosiddetto “problema dell’assegnazione dei crediti”: deve identificare quali neuroni dello studente sono responsabili della ricompensa. Un modo standard per raggiungere questo obiettivo è quello di iniettare la variabilità nell’output degli studenti e rafforzare il fuoco dei neuroni che precedono la ricompensa (vedi per esempio(Fiete et al., 2007) nel contesto del canto degli uccelli). Così, nel nostro modello, il tutor ha un duplice ruolo di fornire sia un segnale istruttivo che la variabilità, come nel canto degli uccelli.
Abbiamo descritto l’output del nostro modello utilizzando un vettore ya(t) in cui sono stati indicizzati i vari canali di uscita (Figura 2A). Nel contesto del controllo del motore un potrebbe indicizzare il muscolo da controllare, o, più astrattamente, diverse caratteristiche dell’uscita del motore, come il passo e l’ampiezza nel caso del canto degli uccelli. L’uscita ya(t) era una funzione dell’attività dei neuroni studenti sj(t). I neuroni degli studenti erano a loro volta guidati dall’attività dei neuroni conduttori ci(t). Lo studente riceveva anche i segnali del tutor per guidare la plasticità; nel songbird, i segnali guida per ogni neurone RA provengono da diversi neuroni LMAN(Canady et al., 1988; Garst-Orozco et al., 2014; Herrmann e Arnold , 1991). Nel nostro modello, abbiamo riassunto l’input netto dal tutor al jth neurone studente come una singola funzione gj(t).10.7554/eLife.20944.003Figure 2.Schematic representation of our rate-based model.(A) I neuroni conduttori sparano raffiche precise, simili ai neuroni HVC negli uccelli canori. Le attività del conduttore e del tutor, c(t) e g(t), forniscono eccitazione ai neuroni degli studenti, che integrano questi input e rispondono in modo lineare, con attività s(t). I neuroni degli studenti ricevono anche un input inibitorio costante, xinh. I neuroni in uscita combinano linearmente le attività di gruppi di neuroni studenti utilizzando i pesi Maj. Le ipotesi di linearità sono state fatte per comodità matematica, ma non sono essenziali per i nostri risultati qualitativi (vedi Appendice).(B). I pesi sinaptici Wij conduttori-studenti sono aggiornati sulla base di una regola di plasticità che dipende da due parametri, α e β, e due tempi, τ1 e τ2 (vedi Equazione (1) e Materiali e metodi). Il segnale del tutor inserisce questa regola come deviazione da una soglia costante θ. La figura mostra come cambiano i pesi sinaptici (ΔW) per un neurone studente che riceve uno scoppio del tutor e uno scoppio del conduttore separati da un breve ritardo. Due diverse scelte di parametri di plasticità sono illustrate nel caso in cui la soglia θ=0. (C)La quantità di disallineamento tra l’uscita del sistema e l’uscita di destinazione è quantificata utilizzando una funzione di perdita (errore). La figura descrive il paesaggio di perdita ottenuto variando i pesi sinaptici Wij e calcolando la funzione di perdita in ogni caso (solo due degli assi di peso sono mostrati). Il punto blu mostra il valore più basso della funzione di perdita, corrispondente alla migliore corrispondenza tra l’uscita del motore e il target, mentre il punto arancione mostra il punto di partenza. La linea tratteggiata mostra come l’apprendimento procederebbe in un approccio di discesa in pendenza, dove i pesi cambiano nella direzione della discesa più ripida nel paesaggio di perdita.DOI:http://dx.doi.org/10.7554/eLife.20944.003
Abbiamo iniziato con un’implementazione del modello basata sul tasso(Figura 2A) che era analiticamente tracciabile ma mediata sulla variabilità del tutor. Abbiamo inoltre preso i neuroni per essere in un regime operativo lineare(Figura 2A) lontano dalla soglia e la saturazione presente nei neuroni reali. Abbiamo poi rilassato queste condizioni e testato i nostri risultati in reti di spiking con parametri iniziali selezionati per imitare i modelli di sparo misurati in uccelli giovani prima dell’apprendimento del canto. Il circuito degli studenti, sia nei modelli basati sul tasso che in quelli basati sullo spiking, includeva un segnale inibitorio globale che aiutava a sopprimere l’attività in eccesso guidata dall’input del conduttore e del tutor in corso. Tale inibizione ricorrente è presente nell’area RA dell’uccello(Spiro et al., 1999). Nel modello di spiking abbiamo implementato la soppressione come inibizione dipendente dall’attività, mentre per i calcoli analitici abbiamo usato un costante bias negativo per i neuroni degli studenti.
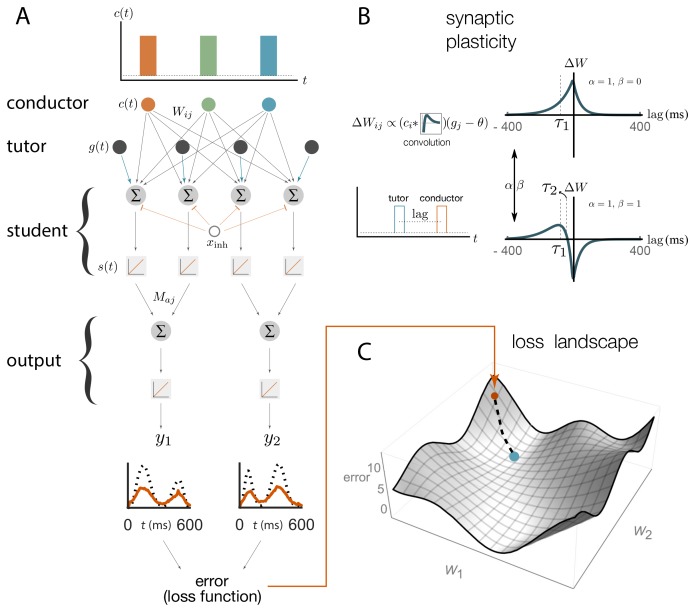
Figura 2.Rappresentazione schematica del nostro modello basato sul tasso.(A) I neuroni conduttori sparano raffiche precise, simili ai neuroni HVC negli uccelli canori. Le attività del conduttore e del tutor, c(t) e g(t), forniscono eccitazione ai neuroni degli studenti, che integrano questi input e rispondono in modo lineare, con attività s(t). I neuroni degli studenti ricevono anche un input inibitorio costante, xinh. I neuroni in uscita combinano linearmente le attività di gruppi di neuroni studenti utilizzando i pesi Maj. Le ipotesi di linearità sono state fatte per comodità matematica, ma non sono essenziali per i nostri risultati qualitativi (vedi Appendice).(B). I pesi sinaptici Wij conduttori-studenti sono aggiornati sulla base di una regola di plasticità che dipende da due parametri, α e β, e due tempi, τ1 e τ2 (vedi Equazione (1) e Materiali e metodi). Il segnale del tutor inserisce questa regola come deviazione da una soglia costante θ. La figura mostra come cambiano i pesi sinaptici (ΔW) per un neurone studente che riceve uno scoppio del tutor e uno scoppio del conduttore separati da un breve ritardo. Due diverse scelte di parametri di plasticità sono illustrate nel caso in cui la soglia θ=0. (C)La quantità di disallineamento tra l’uscita del sistema e l’uscita di destinazione è quantificata utilizzando una funzione di perdita (errore). La figura descrive il paesaggio di perdita ottenuto variando i pesi sinaptici Wij e calcolando la funzione di perdita in ogni caso (solo due degli assi di peso sono mostrati). Il punto blu mostra il valore più basso della funzione di perdita, corrispondente alla migliore corrispondenza tra l’uscita del motore e il target, mentre il punto arancione mostra il punto di partenza. La linea tratteggiata mostra come l’apprendimento procederebbe in un approccio di discesa in pendenza, dove i pesi cambiano nella direzione della discesa più ripida nel paesaggio di perdita.DOI:
http://dx.doi.org/10.7554/eLife.20944.003
Imparare in un modello basato sui tassi
L’apprendimento nel nostro modello è stato abilitato dalla plasticità delle sinapsi conduttore-studente che è stata modulata dai segnali dei neuroni del tutor (Figura 2B). Sono state osservate molte forme diverse di tale plasticità eterosinaptica. Ad esempio, nella plasticità sinaptica basata sul tasso di plasticità sinaptica, un alto tasso di cottura del tutor porta al potenziamento sinaptico e un basso tasso di cottura del tutor porta alla depressione(Chistiakova e Volgushev, 2009; Chistiakova et al., 2014). Nelle regole che dipendono dal tempo, come quella recentemente misurata da Mehaffey e Doupe (2015) in fette di fringuello zebrato RA (vedi Figura 1C), i relativi tempi di arrivo delle esplosioni di picco da diversi percorsi di ingresso impostano il segno del cambiamento sinaptico. Per modellare l’apprendimento che si trova tra questi estremi basati sul tasso e sul tempo, abbiamo introdotto una classe di regole di plasticità regolate da due parametri α e β (vedi anche Materiali e metodi e Figura 2B ):dWijdt=ηc~i(t)(gj(t)-θ),(1)c~i(t)=∫0tdt′ci(t′)[ατ1e-(t-t′)/τ1-βτ2e-(t-t′)/τ2],
dove Wij è il peso della sinapsi dall’iesimo conduttore al jth neurone studente, η è un tasso di apprendimento, θ è una soglia sul tasso di accensione dei neuroni tutor, e τ1 e τ2 sono tempi associati alla plasticità. Questo è simile a una regola STDP, tranne che la dipendenza dall’attività postsinaptica è stata sostituita dalla dipendenza dall’input del tutor. Così la plasticità agisce in modo eterosinaptico, con l’attivazione della sinapsi del tutor-studente che controlla il cambiamento del peso sinaptico conduttore-studente. I tempi τ1 e τ2, così come i coefficienti α e β, possono essere considerati come parametri efficaci che descrivono la plasticità osservata nei neuroni degli studenti. Come tali, essi non hanno necessariamente una semplice corrispondenza in termini di biochimica del meccanismo di plasticità, e il quadro che qui descriviamo non è specificamente legato a tale interpretazione.
Se impostiamo α o β a zero nella nostra regola, Equazione (1), il segno del cambiamento sinaptico è determinato unicamente dalla velocità di accensione del tutor gj(t) rispetto ad una soglia, riproducendo le regole di velocità osservate negli esperimenti. Quando α/β≈1, se il conduttore conduce il tutor, si verifica il potenziamento, mentre i segnali coincidenti portano alla depressione (Figura 2B),che imita i risultati empirici di Mehaffey e Doupe (2015). Per il generale α e β, il segno di plasticità è controllato sia dalla velocità di accensione del tutor rispetto alla linea di base, sia dalla relativa tempistica del tutor e del conduttore. La scala complessiva dei parametri α e β può essere assorbita nel tasso di apprendimento η e così impostiamo α-β=1 in tutte le nostre simulazioni senza perdita di generalità (vedi Materiali e metodi). Si noti che se α e β sono entrambi grandi, può essere che α-β=1 e α/β≈1 anche, come necessario per realizzare la curva di Mehaffey e Doupe (2015) .
Possiamo chiedere come il conduttore-studente pesi Wij (Figura 2A) dovrebbe cambiare per migliorare al meglio l’output ya(t). Abbiamo bisogno prima di tutto di una funzione di perdita L che quantifichi la distanza tra l’uscita corrente ya(t) e l’obiettivo y¯a(t) (Figura 2C). Abbiamo usato una funzione di perdita quadratica, ma altre scelte possono essere incorporate nella nostra struttura (vedi Appendice). L’apprendimento dovrebbe cambiare i pesi sinaptici in modo che la funzione di perdita sia minimizzata, portando ad una buona resa dell’output mirato. Questo può essere ottenuto cambiando i pesi sinaptici nella direzione della discesa più ripida della funzione di perdita(Figura 2C).
Abbiamo usato la regola di plasticità sinaptica dell’equazione (1) per calcolare la variazione complessiva dei pesi, ΔWij, nel corso del programma del motore. Questa è una funzione del corso del tempo del segnale del tutor, gj(t). Non tutte le scelte per il segnale del tutor portano a modifiche dell’uscita del motore che migliorano la corrispondenza con l’obiettivo. Imponendo la condizione che questi cambiamenti seguano la procedura di discesa del gradiente descritta sopra, abbiamo derivato il segnale del tutor che è stato meglio abbinato alla regola di plasticità dello studente (derivazione dettagliata in Materiali e metodi). Il risultato è che il miglior tutor per l’apprendimento della discesa in gradiente di guida deve tenere traccia dell’errore motorio(2)ϵj(t)=∑aMaj(ya(t)-y¯a(t))
integrato nel recente passato(3)gj(t)=θ-ζα-β1τtutor∫0tϵj(t′)e-(t-t′)/τtutordt′,
dove Maj sono i pesi che descrivono la relazione lineare tra le attività degli studenti e i risultati motori (Figura 2A) e ζ è un tasso di apprendimento. Inoltre, per un apprendimento efficace, il parametro τtutor che appare in Equazione (3), che quantifica il lasso di tempo in cui le informazioni di errore sono integrate nel segnale del tutor, dovrebbe essere correlato ai parametri di plasticità sinaptica secondo(4)τtutor=τtutor∗,doveτtutor∗≡ατ1-βτ2α-β
è il lasso di tempo ottimale per l’integrazione degli errori.
In breve, l’apprendimento motorio con una regola di plasticità eterosinaptica richiede la convoluzione dell’errore motorio con un kernel la cui scala temporale è legata alla struttura della regola di plasticità, ma è altrimenti indipendente dal programma motorio. Come spiegato più dettagliatamente in Materiali e metodi, questo risultato è derivato in un’approssimazione che presuppone che il segnale del tutor non vari in modo significativo su tempi dell’ordine dei tempi dello studente τ1 e τ2. Data l’equazione (4), ciò implica che si assume τtutor≫τ1,2. Questa è un’approssimazione ragionevole perché le variazioni del segnale del tutor che sono molto più veloci dei tempi dello studente τ1,2 hanno poco effetto sull’apprendimento poiché la regola della plasticità (1) offusca gli input del conduttore su questi tempi.
Apprendimento ineguagliato vs. apprendimento ineguagliato
Il nostro modello basato sul tasso prevede che quando il lasso di tempo in cui le informazioni di errore sono integrate nel segnale del tutor (τtutor) è abbinato alla regola di plasticità dello studente come descritto sopra, l’apprendimento procederà in modo efficiente. Un tutor non corrispondente dovrebbe rallentare o disturbare la convergenza verso l’output desiderato. Per testare questo, abbiamo simulato numericamente il circuito del canto degli uccelli usando il modello lineare della Figura 2A con un’uscita del motore filtrata per riflettere in modo più realistico i tempi di risposta dei muscoli (vedi Materiali e metodi). Abbiamo selezionato le regole di plasticità come descritto nell’Equazione (1) e nella Figura 2B e abbiamo scelto un modello di uscita target da apprendere. Il target è stato scelto per assomigliare alle registrazioni della pressione aria-sac dal canto dei fringuelli zebrati in termini di scorrevolezza e tempi caratteristici(Veit et al., 2011), ma è stato altrimenti arbitrario. Nelle nostre simulazioni, l’output ha tipicamente coinvolto due canali diversi, ognuno con il proprio target, ma per brevità, in cifre abbiamo tipicamente mostrato l’output di uno solo di questi.
Per i nostri calcoli analitici, abbiamo fatto una serie di ipotesi e approssimazioni volte a migliorare la trattabilità, come la linearità del modello e un focus sul regime τtutor≫τ1,2. Questi vincoli possono essere eliminati nelle nostre simulazioni, e in effetti di seguito testiamo il nostro modello numerico in regimi che vanno oltre le approssimazioni fatte nella nostra derivazione. In molti casi, abbiamo scoperto che i risultati di base riguardanti l’abbinamento tutor-studente dal nostro modello analitico rimangono veri anche quando alcune delle ipotesi che abbiamo usato per derivarlo non sono più valide.
Abbiamo testato i tutor che erano abbinati o non abbinati alla regola della plasticità per vedere quanto efficacemente istruivano lo studente. La Figura 3A e il Video 1 online mostrano la convergenza con un tutor abbinato quando il segno di plasticità è determinato dal tasso di licenziamento del tutor. Vediamo che l’output dello studente converge rapidamente verso l’obiettivo. La Figura 3B e il Video 2 mostrano la convergenza con un tutor quando il segno di plasticità è in gran parte determinato dalla relativa tempistica del segnale del tutor e dall’uscita dello studente. Vediamo di nuovo che lo studente convergeva costantemente verso l’uscita desiderata, ma ad un ritmo un po’ più lento rispetto alla Figura 3A.10.7554/eLife.20944.004Figure 3.Learning with matched or mis matched tutor in rate-based simulations.(A) Traccia dell’errore che mostra come l’errore motore medio si è evoluto con il numero di ripetizioni del programma motore per una regola di plasticità basata sulla velocità (α=0) accoppiata con un tutor corrispondente. (Vedi Video 1 online).(B) La traccia dell’errore e l’uscita finale del motore mostrato per una regola di apprendimento basata sul tempo abbinata da un tutor con un lungo periodo di integrazione. (Vedi Video online 2.) Sia in A che in B l’inserto mostra l’uscita finale del motore per uno dei due canali di uscita (linea arancione spessa) rispetto all’uscita di destinazione per quel canale (linea nera tratteggiata). Anche l’uscita sulla prima resa e in altri due stadi di apprendimento indicati dalle frecce arancioni sulla traccia di errore sono mostrati come sottili linee arancioni.(C) Effetti della mancata corrispondenza tra studente e tutor sull’accuratezza della riproduzione. La heatmap mostra l’errore di riproduzione finale dell’uscita del motore dopo 1000 cicli di apprendimento in una simulazione basata sulla velocità in cui uno studente con i parametri α, β, τ1 e τ2 è stato accoppiato con un tutor con la scala dei tempi di memoria τtutor. Sull’asse y, τ1 e τ2 sono stati mantenuti fissi rispettivamente a 80ms e 40ms, mentre α e β sono stati variati (soggetto al vincolo α-β=1; vedi testo). Le diverse scelte di α e β portano a diversi tempi ottimali τtutor* secondo l’equazione (4) . Gli elementi diagonali corrispondono al tutor e allo studente abbinati, τtutor=τtutor*. Si noti che la scala dei colori è logaritmica.(D) Curve di evoluzione degli errori in funzione della mancata corrispondenza tra studente e tutor. Ogni grafico mostra come l’errore nel programma del motore è cambiato durante 1000 cicli di apprendimento per le stesse condizioni mostrate nella heatmap. La regione ombreggiata in rosa chiaro mostra simulazioni in cui il disallineamento tra studente e tutor ha portato ad un peggioramento invece di migliorare le prestazioni durante l’apprendimento.DOI:http://dx.doi.org/10.7554/eLife.20944.004Video1.Evoluzione della potenza del motore durante l’apprendimento in una simulazione basata sulla velocità, utilizzando una regola di plasticità basata sulla velocità (α=0) accoppiata con un tutor corrispondente .DOI:http://dx.doi.org/10.7554/eLife.20944.00510.7554/eLife.20944.005Video2.Evoluzione della potenza motoria durante l’apprendimento in una simulazione basata sulla velocità utilizzando una regola di plasticità basata sul tempo (α≈β) accoppiata con un tutor corrispondente.Questo video si riferisce alla Figura 3B.DOI:http://dx.doi.org/10.7554/eLife.20944.00610.7554/eLife.20944.006
Per testare gli effetti della mancata corrispondenza tra tutor e studente, abbiamo usato tutor con tempi che non corrispondevano all’equazione (4). Tutte le regole di plasticità dello studente avevano le stesse costanti di tempo effettivo τ1 e τ2, ma parametri diversi α e β (vedi Equazione 1), soggetto al vincolo α-β=1 descritto nella sezione precedente. Diversi tutor avevano diverse scale temporali di memoria τtutor (Equazione3). La figura 3C e D dimostrano che l’apprendimento è stato più rapido per coppie tutor-studente ben assortite (il quartiere diagonale, dove τtutor≈τtutor*). Quando il tempo di integrazione dell’errore del tutor era più breve del valore corrispondente in Equazione (4), τtutor < τtutor∗, l’apprendimento era spesso completamente interrotto (molte coppie al di sotto della diagonale in Figura 3C e D). Quando il tempo di integrazione dell’errore del tutor era più lungo del valore corrispondente in Equazione (4), l’apprendimento τtutor > τtutor∗ è stato rallentato. La figura 3C mostra anche che una certa quantità di disallineamento tra la scala dei tempi di integrazione dell’errore del tutor τtutor e la scala dei tempi corrispondente τtutor* implicita dalla regola di plasticità dello studente è tollerata dal sistema. È interessante notare che la banda diagonale su cui l’apprendimento è efficace nella Figura 3C è approssimativamente di larghezza costante – si noti che la scala su entrambi gli assi è logaritmica, in modo che questo significa che il tutor errore di integrazione della scala dei tempi di errore τtutor deve essere all’interno di un fattore costante della scala dei tempi ottimale τtutor* per un buon apprendimento. Vediamo anche che la rottura nell’apprendimento è più brusca quando τtutor < τtutor∗ rispetto al regime opposto.
Una caratteristica interessante dei risultati della Figura 3C e D è che la differenza di prestazioni tra coppie accoppiate e non accoppiate diventa meno pronunciata per tempi più brevi di circa 100ms. Ciò è dovuto al fatto che la regola della plasticità(Equazione 1) si attenua implicitamente su tempi dell’ordine di τ1,2, che nelle nostre simulazioni erano pari a τ1=80ms, τ2=40ms. Quindi, le variazioni del segnale del tutor su tempi più brevi hanno poco effetto sull’apprendimento. L’utilizzo di valori diversi per i tempi effettivi τ1,2 che descrivono la regola di plasticità può aumentare o diminuire la gamma di parametri su cui l’apprendimento è robusto contro gli squilibri tra tutor e studenti (vedi Appendice).
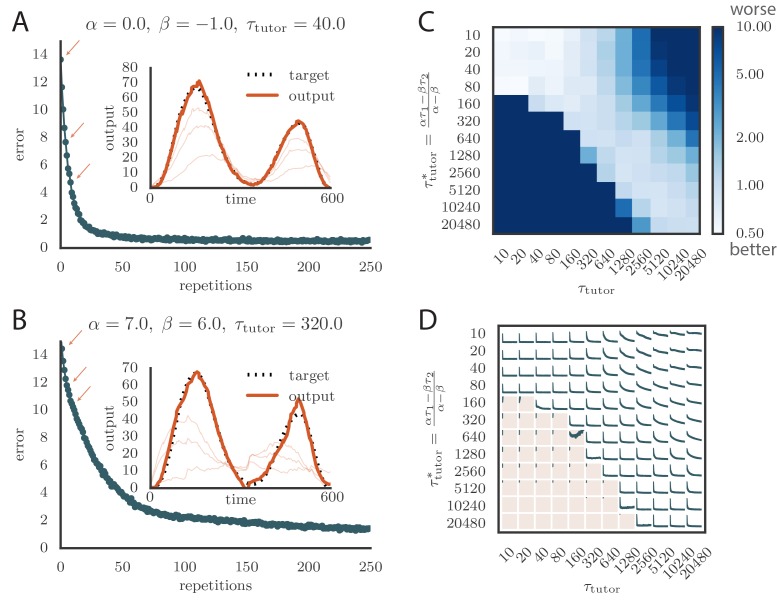
Figura 3.Figura 3. Apprendimento con tutor abbinati o non abbinati in simulazioni basate sui tassi.(A) Traccia dell’errore che mostra come l’errore motorio medio si è evoluto con il numero di ripetizioni del programma motorio per una regola di plasticità basata sulla velocità (α=0) accoppiata con un tutor corrispondente. (Vedi Video 1 online).(B) La traccia dell’errore e l’uscita finale del motore mostrato per una regola di apprendimento basata sul tempo abbinata da un tutor con un lungo periodo di integrazione. (Vedi Video online 2.) Sia in A che in B l’inserto mostra l’uscita finale del motore per uno dei due canali di uscita (linea arancione spessa) rispetto all’uscita di destinazione per quel canale (linea nera tratteggiata). Anche l’uscita sulla prima resa e in altri due stadi di apprendimento indicati dalle frecce arancioni sulla traccia di errore sono mostrati come sottili linee arancioni.(C) Effetti della mancata corrispondenza tra studente e tutor sull’accuratezza della riproduzione. La heatmap mostra l’errore di riproduzione finale dell’uscita del motore dopo 1000 cicli di apprendimento in una simulazione basata sulla velocità in cui uno studente con i parametri α, β, τ1 e τ2 è stato accoppiato con un tutor con la scala dei tempi di memoria τtutor. Sull’asse y, τ1 e τ2 sono stati mantenuti fissi rispettivamente a 80ms e 40ms, mentre α e β sono stati variati (soggetto al vincolo α-β=1; vedi testo). Le diverse scelte di α e β portano a diversi tempi ottimali τtutor* secondo l’equazione (4) . Gli elementi diagonali corrispondono al tutor e allo studente abbinati, τtutor=τtutor*. Si noti che la scala dei colori è logaritmica.(D) Curve di evoluzione degli errori in funzione della mancata corrispondenza tra studente e tutor. Ogni grafico mostra come l’errore nel programma del motore è cambiato durante 1000 cicli di apprendimento per le stesse condizioni mostrate nella heatmap. La regione ombreggiata in rosa chiaro mostra simulazioni in cui il disallineamento tra studente e tutor ha portato ad un peggioramento invece di migliorare le prestazioni durante l’apprendimento.DOI:
http://dx.doi.org/10.7554/eLife.20944.004

Video 1.Evoluzione della potenza del motore durante l’apprendimento in una simulazione basata sul tasso, utilizzando una regola di plasticità basata sul tasso (α=0) accoppiata con un tutor corrispondente.Questo video si riferisce alla Figura 3A.DOI:
http://dx.doi.org/10.7554/eLife.20944.005

Video 2.2. Evoluzione della potenza del motore durante l’apprendimento in una simulazione basata sul tasso, utilizzando una regola di plasticità basata sul tempo (α≈β) accoppiata con un tutor di corrispondenza.Questo video si riferisce alla Figura 3B.DOI:
http://dx.doi.org/10.7554/eLife.20944.006
Apprendimento robusto con non linearità
Nel modello di cui sopra, i tassi di licenziamento per il tutor sono stati fatti crescere tanto quanto necessario per implementare l’apprendimento più efficiente. Tuttavia, i tassi di cottura di neuroni realistici in genere saturazione di neuroni realistici a qualche limite fisso. Per testare gli effetti di questa non linearità nel tutor, abbiamo passato l’attività ideale del tutor(Equazione 3) attraverso una non linearità sigmoidale,(5)g~j(t)=θ-ρtanhζα-β1τtutor∫0tϵj(t′)e-(t-t′)/τtutordt′.
dove 2ρ è l’intervallo dei tassi di sparo. In genere abbiamo scelto θ=ρ=80Hz per limitare le frequenze nell’intervallo 0-160 Hz (Ölveczky et al., 2005; Garst-Orozco et al., 2014). L’apprendimento è rallentato con questo cambiamento(Figura 4A e Video 3 online) come risultato del tutor che ha saturato i tassi di cottura quando il disallineamento tra l’uscita del motore e l’uscita di destinazione era grande. Tuttavia, la precisione della resa finale non è stata influenzata dalla saturazione del tutor(Figura 4A, inserto). Un effetto interessante si è verificato quando è stato imposto il vincolo della velocità di scatto ad un tutor con una lunga durata di memoria. Quando questo accadeva e l’errore motore era grande, il segnale del tutor si saturava e smetteva di crescere in relazione all’errore motore prima della fine del programma motore. Nel caso estremo di tempi di integrazione molto lunghi, l’apprendimento è diventato sequenziale: le prime caratteristiche dell’output sono state apprese prima, prima di affrontare le caratteristiche successive, come nella Figura 4B e nel Video 4 online. Questo ricorda la regola di apprendimento descritta in(Memmesheimer et al., 2014).10.7554/eLife.20944.007Figure 4.Effetti dell’aggiunta di un vincolo sul tasso di apprendimento del tutor alle simulazioni.(A) L’apprendimento è stato rallentato dal vincolo del tasso di apprendimento, ma l’accuratezza della resa finale è rimasta la stessa (inset, mostrato qui per uno dei due canali di output simulati). Qui α=0, β=-1, e τtutor=τtutor*=40ms. (Vedi Video online 3.)(B) L’apprendimento sequenziale si è verificato quando è stato imposto il vincolo di velocità di sparo ad un tutor con una scala di memoria lunga. Le trame mostrano l’evoluzione dell’uscita del motore per uno dei due canali che sono stati utilizzati nella simulazione. Qui α=24, β=23 e τtutor=τtutor*=1000ms. (Vedi il video online 4.).DOI:http://dx.doi.org/10.7554/eLife.20944.007Video3.Effetti dell’aggiunta di un vincolo sui tassi di accensione del tutor sull’evoluzione della potenza del motore durante l’apprendimento in una simulazione basata sui tassi. Questo video si riferisce alla Figura 4A.DOI:http://dx.doi.org/10.7554/eLife.20944.00810.7554/eLife.20944.008Video4.Evolution of motor output showing sequential learning in a rate-based simulation when the firing rate constraint is imposed on a tutor with a long memory time scale.This video relates to Figure 4B.DOI:http://dx.doi.org/10.7554/eLife.20944.00910.7554/eLife.20944.009
Le non linearità possono influenzare in modo simile le attività dei neuroni degli studenti. Il nostro modello può essere facilmente esteso per descrivere l’apprendimento efficiente anche in questo caso. Il risultato chiave è che per un apprendimento efficiente, la regola della plasticità sinaptica dovrebbe dipendere non solo dal tutor e dal conduttore, ma anche dall’attività dei neuroni postsinaptici degli studenti (dettagli in Appendice). Tale dipendenza dall’attività postsinaptica è comunemente vista negli esperimenti(Chistiakova e Volgushev, 2009; Chistiakova et al., 2014).
La relazione tra le attivazioni neuronali degli studenti sj(t) e le uscite motorie ya(t) (Figura 2A) è in generale anche non lineare. Rispetto all’ipotesi lineare che abbiamo usato, l’effetto di una non linearità monotona, ya=Na(∑jMajsj), con Na una funzione crescente, è simile alla modifica della funzione di perdita L, e non cambia significativamente i nostri risultati (vedi Appendice). Abbiamo anche verificato che l’imposizione di un vincolo di rettifica che impone che i pesi del conduttore-studente Wij debbano essere positivi non modifica i nostri risultati (vedi Appendice). Questo dimostra che il nostro modello continua a lavorare con sinapsi biologicamente realistiche che non possono cambiare segno da eccitante ad inibitorio durante l’apprendimento.
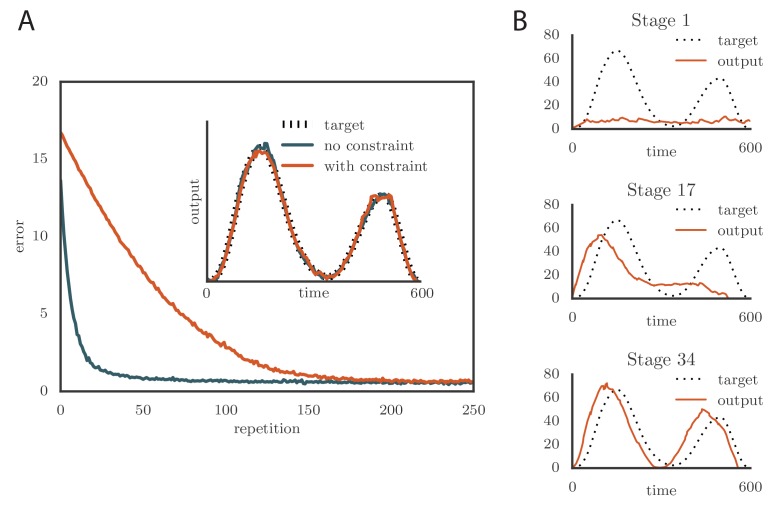
Figura 4.Effetti dell’aggiunta di un vincolo sul tasso di cottura del tutor alle simulazioni.(A) L’apprendimento è stato rallentato dal vincolo del rateo di cottura, ma l’accuratezza della resa finale è rimasta la stessa (in questo esempio, mostrato qui per uno dei due canali di uscita simulati). Qui α=0, β=-1, e τtutor=τtutor*=40ms. (Vedi Video online 3.)(B) L’apprendimento sequenziale si è verificato quando è stato imposto il vincolo di velocità di sparo ad un tutor con una scala di memoria lunga. Le trame mostrano l’evoluzione dell’uscita del motore per uno dei due canali che sono stati utilizzati nella simulazione. Qui α=24, β=23 e τtutor=τtutor*=1000ms. (Vedi il video online 4.).DOI:
http://dx.doi.org/10.7554/eLife.20944.007

Video 3.3. Effetti dell’aggiunta di un vincolo sui tassi di scatto del tutor sull’evoluzione della potenza del motore durante l’apprendimento in una simulazione basata sui tassi.La regola della plasticità qui era basata sul tasso (α=0). Questo video si riferisce alla Figura 4A.DOI:
http://dx.doi.org/10.7554/eLife.20944.008

Video 4.Evoluzione dell’uscita del motore che mostra l’apprendimento sequenziale in una simulazione basata sul tasso, quando il vincolo del tasso di accensione è imposto ad un tutor con un lungo periodo di memoria.Questo video si riferisce alla Figura 4B.DOI:
http://dx.doi.org/10.7554/eLife.20944.009
Neuroni a spillo e canto degli uccelli
Per applicare il nostro modello all’apprendimento vocale negli uccelli, abbiamo esteso la nostra analisi alle reti di neuroni a spillo. Gli uccelli canori giovanili producono un “balbettio” che converge attraverso l’apprendimento in una canzone per adulti che assomiglia fortemente alla canzone del tutor. Questo si riflette nei modelli di spiking canoro allineati nell’area pre-motoria RA, che diventano più stereotipati e si raggruppano in scoppi più brevi e meglio definiti man mano che l’uccello matura(Figura 5A). Abbiamo testato se il nostro modello è in grado di riprodurre le statistiche chiave dello spiking in RA nel corso dell’apprendimento del canto. In questo contesto, la nostra teoria dell’apprendimento efficiente, derivata in uno scenario basato sul tasso, prevede una relazione specifica tra il segnale di insegnamento incorporato nei modelli di sparo LMAN e la regola di plasticità implementata nella RA. Abbiamo testato se queste previsioni hanno continuato a tenere nel contesto dello spiking.10.7554/eLife.20944.010Figure 5.Results from simulations in spiking neural networks.(A) Spike patterns registrati da zebra finch RA durante la produzione di canzoni, per un giovane (in alto) e un adulto (in basso). Ogni colore corrisponde ad un singolo neurone, e vengono mostrati i picchi allineati per sei rappresentazioni della canzone. Adattato da Ölveczky et al. (2011).(B) Modelli di punte di neuroni di studenti modello nelle nostre simulazioni, per i modelli non addestrati (in alto) e addestrati (in basso). La formazione utilizzato α = 1, β = 0, e τtutor = 80ms, e correva per 600 iterazioni della canzone. Ogni neurone modello corrisponde ad un diverso canale di uscita della simulazione. In questo caso, gli obiettivi per ogni canale sono stati scelti per approssimare approssimativamente il corso del tempo osservato nelle registrazioni neurali.(C) Progressione dell’errore di riproduzione nella simulazione di spiking in funzione del numero di ripetizioni per le stesse condizioni del pannello B. L’inserto mostra l’accuratezza della riproduzione nel modello addestrato per uno dei canali di uscita. (Vedi Video online 5.)(D) Effetti della mancata corrispondenza tra studente e tutor sulla precisione di riproduzione nel modello di spiking. La heatmap mostra l’errore di riproduzione finale dell’uscita del motore dopo 1000 cicli di apprendimento in una simulazione di spiking in cui uno studente con i parametri α, β, τ1 e τ2 è stato accoppiato con un tutor con la scala dei tempi di memoria τtutor. Sull’asse y, τ1 e τ2 sono stati mantenuti fissi a 80ms e 40ms, rispettivamente, mentre α e β sono stati variati (soggetto al vincolo α-β=1; vedere la sezione “Apprendimento in un modello basato sul tasso”). Diverse scelte di α e β portano a diversi tempi ottimali τtutor* secondo l’equazione (4) . Gli elementi diagonali corrispondono al tutor e allo studente abbinati, τtutor=τtutor*. Si noti che la scala dei colori è logaritmica.DOI:http://dx.doi.org/10.7554/eLife.20944.010Video5.Evoluzione della potenza del motore durante l’apprendimento in una simulazione di picco. I parametri della regola di plasticità erano α=1, β=0, e il tutor aveva una scala temporale corrispondente τtutor=τtutor*=80ms. Questo video si riferisce alla Figura 5C.DOI:http://dx.doi.org/10.7554/eLife.20944.01110.7554/eLife.20944.011
In seguito agli esperimenti di Hahnloser et al. (2002), abbiamo modellato ogni neurone in HVC (il conduttore) come sparando una breve e precisa raffica di 5-6 picchi in un singolo momento nel programma del motore. Così la popolazione di neuroni HVC ha prodotto una base temporale precisa per la canzone. I neuroni LMAN (tutor) sono noti per avere schemi di sparo altamente variabili che facilitano la sperimentazione, ma contengono anche un bias correttivo(Andalman e Fee, 2009). Così abbiamo modellato l’LMAN come la produzione di treni di Poisson non omogenei con una velocità di sparo dipendente dal tempo data da Equation (5) nel nostro modello. Anche se biologicamente ci sono diversi neuroni LMAN che proiettano ad ogni neurone RA, abbiamo semplificato ancora una volta ‘sommando’ gli input LMAN in un singolo, efficace neurone tutor, in modo simile all’approccio di (Fiete etal., 2007). Le sinapsi LMAN-RA sono state modellate in un approccio basato sulla corrente come una miscela di recettori AMPA e NMDA, seguendo i dati di songbird(Garst-Orozco et al., 2014; Stark e Perkel, 1999). I pesi iniziali per tutte le sinapsi sono stati sintonizzati per produrre modelli di sparo RA che assomigliano agli uccelli giovani(Ölveczky et al., 2011), soggetti ai vincoli delle misurazioni dirette nelle registrazioni a fette (Garst-Orozcoet al., 2014) (vedi Materiali e metodi per i dettagli, e la Figura 5B per un confronto tra le registrazioni neurali e lo spiking nel nostro modello). In contrasto con il costante bias inibitorio che abbiamo usato nelle nostre simulazioni basate sul tasso, per le simulazioni di spiking abbiamo scelto un’inibizione globale dipendente dall’attività per i neuroni RA. Abbiamo anche testato che un bias costante produceva risultati simili (vedi Appendice).
Gli aggiornamenti della forza sinaptica hanno seguito la stessa dinamica a due scale che è stata utilizzata nei modelli basati sul tasso(Figura 2B). I ratei di cottura ci(t) e gj(t) che appaiono nell’equazione della plasticità sono stati calcolati nel modello di spiking filtrando i treni di spike dai neuroni conduttori e tutori con kernel esponenziali. I pesi sinaptici erano vincolati ad essere non negativi. (Vedi Materiali e metodi per i dettagli).
Finché i tempi di integrazione degli errori del tutor non erano troppo lunghi, l’apprendimento procedeva in modo efficace quando i tempi di integrazione degli errori del tutor e la regola di plasticità dello studente erano abbinati (vedi Figura 5C e Video 5 online), con disallineamenti che rallentavano o abolivano l’apprendimento, proprio come nel nostro studio basato sui tassi (confrontare la Figura 5D con la Figura 3C). Il tasso di apprendimento e l’accuratezza dello stato addestrato erano più bassi nel modello di picco rispetto al modello basato sul tasso. La minore accuratezza nasce dal fatto che i neuroni del tutor sparano stocasticamente, a differenza dei neuroni deterministici utilizzati nelle simulazioni basate sul tasso. La natura stocastica del fuoco del tutor ha anche portato ad una diminuzione della precisione di apprendimento come il tutor errore di integrazione della scala di tempo di integrazione del tutor τtutor aumentato (Figura 5D). Questo avviene attraverso due effetti correlati: (1) il rapporto segnale-rumore nel segnale guida del tutor diminuisce man mano che τtutor aumenta una volta che il tempo di integrazione dell’errore del tutor è più lungo della durata T del programma motore (vedi Appendice); e (2) le fluttuazioni dei pesi del conduttore-studente portano alcuni pesi ad essere bloccati a 0 a causa del vincolo di positività, che porta il programma motore a superare l’obiettivo (vedi Appendice). Quest’ultimo effetto può essere ridotto sia consentendo pesi negativi, sia cambiando l’uscita del motore in un’architettura push-pull in cui alcuni neuroni degli studenti migliorano l’uscita mentre altri la inibiscono. L’effetto del rapporto segnale-rumore può essere attenuato aumentando il guadagno del segnale del tutor, che inibisce l’apprendimento precoce, ma migliora la qualità del segnale guida nelle ultime fasi del processo di apprendimento. Vale anche la pena sottolineare che questi effetti diventano rilevanti solo quando il tempo di integrazione dell’errore del tutor τtutor diventa significativamente più lungo della durata del programma motore, T, che per un motivo di birdsong sarebbe di circa 1 s.
Il picco nel nostro modello tende ad essere un po’ più regolare di quello delle registrazioni (confrontare la Figura 5A e la Figura 5B). Ciò potrebbe essere dovuto a fonti di rumore presenti nel cervello che non abbiamo modellato. Un dettaglio che il nostro modello non cattura è il fatto che molti picchi LMAN si verificano nelle esplosioni, mentre nella nostra simulazione lo sparo LMAN è Poisson. Le esplosioni hanno maggiori probabilità di produrre picchi nei neuroni RA a valle, in particolare a causa delle dinamiche NMDA, e quindi un LMAN a raffica sarà più efficace nell’iniettare la variabilità nella RA(Kojima et al., 2013). Piccole imprecisioni nell’allineare i picchi registrati alla canzone sono anche suscettibili di contribuire apparente variabilità tra le esecuzioni negli esperimenti. In effetti, alcune delle variabilità della Figura 5A sembrano essere dovute alla distorsione del tempo e agli spostamenti temporali globali che non sono stati completamente corretti.
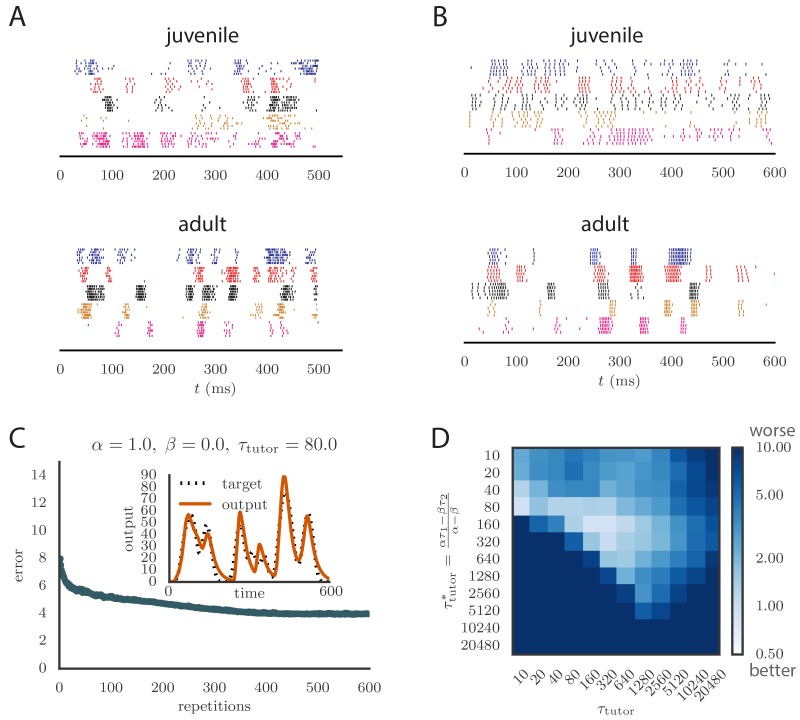
Figura 5.Risultati di simulazioni in reti neurali a picco.(A) Schemi di picco registrati dal fringuello zebrato RA durante la produzione di canzoni, per un giovane (in alto) e un adulto (in basso). Ogni colore corrisponde ad un singolo neurone, e vengono mostrati i picchi allineati per sei rappresentazioni della canzone. Adattato da Ölveczky et al. (2011).(B) Modelli di punte di neuroni di studenti modello nelle nostre simulazioni, per i modelli non addestrati (in alto) e addestrati (in basso). La formazione utilizzato α = 1, β = 0, e τtutor = 80ms, e correva per 600 iterazioni della canzone. Ogni neurone modello corrisponde ad un diverso canale di uscita della simulazione. In questo caso, gli obiettivi per ogni canale sono stati scelti per approssimare approssimativamente il corso del tempo osservato nelle registrazioni neurali.(C) Progressione dell’errore di riproduzione nella simulazione di spiking in funzione del numero di ripetizioni per le stesse condizioni del pannello B. L’inserto mostra l’accuratezza della riproduzione nel modello addestrato per uno dei canali di uscita. (Vedi Video online 5.)(D) Effetti della mancata corrispondenza tra studente e tutor sulla precisione di riproduzione nel modello di spiking. La heatmap mostra l’errore di riproduzione finale dell’uscita del motore dopo 1000 cicli di apprendimento in una simulazione di spiking in cui uno studente con i parametri α, β, τ1 e τ2 è stato accoppiato con un tutor con la scala dei tempi di memoria τtutor. Sull’asse y, τ1 e τ2 sono stati mantenuti fissi a 80ms e 40ms, rispettivamente, mentre α e β sono stati variati (soggetto al vincolo α-β=1; vedere la sezione “Apprendimento in un modello basato sul tasso”). Diverse scelte di α e β portano a diversi tempi ottimali τtutor* secondo l’equazione (4) . Gli elementi diagonali corrispondono al tutor e allo studente abbinati, τtutor=τtutor*. Si noti che la scala dei colori è logaritmica.DOI:
http://dx.doi.org/10.7554/eLife.20944.010

Video 5.Evoluzione dell’uscita del motore durante l’apprendimento in una simulazione di spiking.I parametri della regola di plasticità erano α=1, β=0, e il tutor aveva una scala temporale corrispondente τtutor=τtutor*=80ms. Questo video si riferisce alla Figura 5C.DOI:
http://dx.doi.org/10.7554/eLife.20944.011
Apprendimento robusto con errori di assegnazione dei crediti
Il calcolo dell’uscita del tutor nella nostra regola prevedeva la stima dell’errore del motore ϵj da Equation (2). Questo richiedeva la conoscenza dell’assegnazione tra le attività degli studenti e l’output del motore, che nel nostro modello era rappresentato dalla matrice Maj (Figura 2A). Nelle nostre simulazioni, tipicamente abbiamo scelto un compito in cui ogni neurone dell’allievo contribuiva ad un singolo canale di uscita, mimando i risultati empirici per i neuroni in RA di uccelli. Matematicamente, questo implica che ogni colonna di Maj conteneva un singolo elemento non zero. Nella Figura 6A, mostriamo cosa è successo nel modello basato sul tasso quando il tutor ha erroneamente assegnato una certa frazione dei neuroni all’uscita sbagliata. In particolare, abbiamo considerato due canali di uscita, y1 e y2, con metà dei neuroni degli studenti che contribuiscono solo a y1 e l’altra metà che contribuisce solo a y2. Abbiamo poi strapazzato una frazione ρ di questo compito quando abbiamo calcolato l’errore del motore, in modo che il tutor avesse effettivamente una conoscenza imperfetta della relazione studente-uscita. La figura 6A mostra che l’apprendimento è robusto a questo tipo di errata assegnazione anche per valori abbastanza grandi della frazione di errore ρ fino a circa il 40%, ma si deteriora rapidamente quando questa frazione si avvicina al 50%.10.7554/eLife.20944.012Figure 6.Credit assignment and reinforcement learning.(A) Effetti dell’errata assegnazione del credito sull’apprendimento in una simulazione basata sul tasso. Qui, il sistema ha appreso sequenze di output per due canali indipendenti. I pesi di uscita degli studenti Maj sono stati scelti in modo che il tutor abbia erroneamente assegnato una frazione dei neuroni degli studenti ad un canale di uscita diverso da quello su cui ha effettivamente mappato. Il grafico mostra come la precisione dell’uscita del motore dopo 1000 passi di apprendimento dipendeva dalla frazione di credito erroneamente assegnata.(B) Curva di apprendimento e uscita del motore allenato (inset) per uno dei canali che mostra l’apprendimento a due fasi di rinforzo per il tutor senza memoria (τtutor=0). La precisione del modello addestrato è buona come nel caso in cui si è supposto che il tutor abbia un modello perfetto della relazione studente-uscita. Tuttavia, la velocità di apprendimento è ridotta. (Vedi Video online 6.)(C) Curva di apprendimento e uscita del motore addestrato (inset) per uno dei canali di uscita che mostra l’apprendimento a due fasi di rinforzo quando il circuito del tutor ha bisogno di integrare le informazioni sull’errore del motore in un certo lasso di tempo. Anche in questo caso l’apprendimento è stato lento, ma la precisione dello stato addestrato è rimasta invariata. (Vedi Video online 7.)(D) Evoluzione del numero medio di ingressi HVC per ogni neurone RA con l’apprendimento in un esempio di rinforzo. Le sinapsi sono state considerate potate se hanno ammesso una corrente inferiore a 1 nA dopo un picco presinaptico nelle nostre simulazioni.DOI:http://dx.doi.org/10.7554/eLife.20944.012Video6.Evoluzione dell’uscita del motore durante l’apprendimento in una simulazione di spiking con un tutor di rinforzo.Qui il tutor era senza memoria (τtutor=0). Questo video si riferisce alla Figura 6B.DOI:http://dx.doi.org/10.7554/eLife.20944.01310.7554/eLife.20944.013Video7.Evoluzione dell’output del motore durante l’apprendimento in una simulazione di spiking con un tutor di rinforzo.Qui il tutor aveva bisogno di integrare le informazioni sull’errore del motore su una scala temporale τtutor=440ms. Questo video si riferisce alla Figura 6C.DOI:http://dx.doi.org/10.7554/eLife.20944.01410.7554/eLife.20944.014
A causa di fattori ambientali che influenzano lo sviluppo di diversi individui in modi diversi, è improbabile che la mappatura della produttività degli studenti possa essere innata. Come tale, il circuito di tutor deve imparare la mappatura. Infatti, è noto che LMAN nell’uccello riceve un segnale di valutazione indiretta tramite l’ Area X, che potrebbe essere utilizzato per effettuare questo apprendimento(Andalman e Fee, 2009; Gadagkar et al., 2016; Hoffmann et al., 2016; Kubikova et al., 2010). Un modo in cui questo può essere realizzato è attraverso un paradigma di rinforzo. Abbiamo quindi considerato una regola di apprendimento in cui il circuito dei tutor riceve un segnale di ricompensa che gli permette di dedurre la mappatura delle uscite degli studenti. In generale l’uscita del circuito tutor dovrebbe dipendere da un integrale dell’errore motorio, come in Equazione (3), per istruire al meglio lo studente. Per semplicità, iniziamo con il caso senza memoria, τtutor=0, in cui solo il valore istantaneo dell’errore motore si riflette nel segnale del tutor; mostriamo poi come generalizzare questo per τtutor > 0.
Come prima, abbiamo preso i neuroni del tutor per licenziare i picchi di Poisson con tassi dipendenti dal tempo fj(t), che sono stati inizializzati arbitrariamente. A causa delle fluttuazioni stocastiche, l’attività effettiva del tutor in un dato processo, gj(t), differisce in qualche modo dalla media, g¯j(t). Indicando la differenza con ξj(t)=gj(t)-g¯j(t), la regola di aggiornamento per le percentuali di licenziamento del tutor è stata data da(6)Δfj(t)=ηtutor(R(t)-R¯)ξj(t),
dove ηtutor è un tasso di apprendimento, R(t) è il segnale di ricompensa istantanea, e R¯ è la sua media sulle recenti interpretazioni del programma del motore. Nella nostra implementazione, R¯ si ottiene convolgendo R(t) con un kernel esponenziale (scala temporale = 1 s). La ricompensa R(tmax) alla fine di una resa diventa la linea di base all’inizio della resa successiva R(0). La linea di base g¯j(t) dell’attività del tutor è calcolata facendo la media delle rese recenti del brano con pesi in decadimento esponenziale (un e-fold di decadimento ogni cinque rese). Ulteriori dettagli sull’implementazione sono disponibili nel nostro codice all’indirizzo https://github.com/ttesileanu/twostagelearning(Teşileanu, 2016) (con una copia archiviata all’indirizzo https://github.com/elifesciences-publications/twostagelearning).
L’intuizione alla base di questa regola è che, ogni volta che una fluttuazione nell’attività del tutor porta ad una ricompensa migliore della media (R(t) > R¯), il tasso di licenziamento del tutor cambia nella direzione della fluttuazione per le prove successive, “congelando” il miglioramento. Al contrario, il tasso di cottura si allontana dalle direzioni in cui le fluttuazioni tendono a ridurre la ricompensa.
Per testare la nostra regola di apprendimento, abbiamo eseguito delle simulazioni utilizzando questa strategia di rinforzo e abbiamo scoperto che l’apprendimento converge di nuovo verso una resa accurata dell’output target(Figura 6B, Inset e Video 6 online). Il numero di ripetizioni necessarie per l’addestramento è notevolmente aumentato rispetto al caso in cui l’assegnazione del credito è assunta nota dal circuito del tutor (confrontare la Figura 6B con la Figura 5C). Questo perché il tutor deve utilizzare molti cicli di formazione per la sperimentazione prima di poter guidare la plasticità conduttore-studente. Il tasso di apprendimento nel nostro modello è simile a quello dell’uccello canoro(cioè, ordina 10.000 ripetizioni per l’apprendimento, dato che un fringuello zebrato canta tipicamente circa 1000 ripetizioni del suo canto ogni giorno, e ci vuole circa un mese per sviluppare completamente il canto degli adulti).
A causa del tempo di allenamento extra necessario al tutor per adattare il suo segnale, l’uscita del motore nelle nostre simulazioni basate sulla ricompensa tende inizialmente a superare l’obiettivo (portando all’incrinatura dell’errore a circa 2000 ripetizioni nella Figura 6B). È interessante notare che la successiva riduzione dell’uscita che porta alla convergenza del programma del motore, combinata con il vincolo di positività sulle forze sinaptiche, porta alla potatura di molte connessioni conduttore-studente (Figura 6D). Questo rispecchia gli esperimenti sugli uccelli canori, dove il numero di connessioni tra HVC e RA aumenta prima con l’apprendimento e poi diminuisce(Garst-Orozco et al., 2014).
La regola di rinforzo descritta sopra risponde solo ai valori istantanei del segnale di ricompensa e alle fluttuazioni della frequenza di sparo del tutor. In generale, un apprendimento efficace richiede che il tutor mantenga una traccia di memoria della sua attività su una scala temporale τtutor > 0, come in Equazione (4). Per raggiungere questo obiettivo nel paradigma del rinforzo, possiamo usare una semplice generalizzazione di Equazione (6) dove la regola dell’aggiornamento viene filtrata sulla scala temporale della memoria del tutor:(7)Δfj(t)=ηtutor1τtutor∫tdt′(R(t′)-R¯)ξj(t′)e-(t-t′)/τtutor.
Abbiamo testato che questa regola porta ad un apprendimento efficace se accoppiato con lo studente corrispondente, cioè uno per il quale l’Equazione (4) è obbedito(Figura 6C e Video 7 online).
Le regole di rinforzo qui proposte si riferiscono alle regole di apprendimento di(Fiete e Seung, 2006; Fiete et al., 2007) e(Farries e Fairhall, 2007). Tuttavia, questi modelli si sono concentrati sull’apprendimento in un unico passaggio, invece dell’architettura a due fasi che abbiamo studiato. In particolare, in Fiete et al. (2007), si è ipotizzato che l’area LMAN generasse puro rumore di Poisson e l’apprendimento di rinforzo ha avuto luogo presso le sinapsi HVC-RA. Nel nostro modello, che è in migliore accordo con le recenti evidenze relative al ruolo di RA e LMAN nel canto degli uccelli(Andalman e Fee, 2009), l’apprendimento di rinforzo avviene prima nel percorso del proencefalo anteriore (AFP), di cui LMAN è l’output. Una regola di plasticità eterosinaptica, indipendente dal premio, solidifica poi le informazioni in RA.
Nelle nostre simulazioni, i neuroni del tutor sparano punte di Poisson con tassi specifici dipendenti dal tempo che cambiano durante l’apprendimento. Il tempo dei tassi di accensione in ogni ripetizione deve essere memorizzato da qualche parte nel cervello. Infatti, nel songbird, ci sono proiezioni indirette da HVC a LMAN, passando attraverso i gangli basali (Area X) e la divisione dorso-laterale del talamo mediale (DLM) nella via anteriore proencefalica (Figura 1A)(Perkel, 2004). Queste sinapsi potrebbero memorizzare la necessaria dipendenza dal tempo dei tassi di cottura del tutor. Inoltre, le stesse sinapsi possono fornire l’input di base temporale che garantirebbe la sincronia tra lo sparo LMAN e l’uscita RA, come necessario per l’apprendimento. La nostra regola di apprendimento di rinforzo per l’area del tutor, Equazione (6), può essere vista come un modello efficace per la plasticità nelle proiezioni tra HVC, Area X, DLM e LMAN, come in Fee e Goldberg (2011). In questa immagine, le connessioni indirette HVC-LMAN si comportano in qualche modo come le “sinapsi edonistiche” di Seung (2003), anche se qui usiamo un modello sinaptico più semplice. L’implementazione dell’integrale da Equation (7) richiederebbe un ulteriore circuito ricorrente in LMAN che va oltre lo scopo di questo documento, ma sarebbe interessante da indagare nel lavoro futuro.
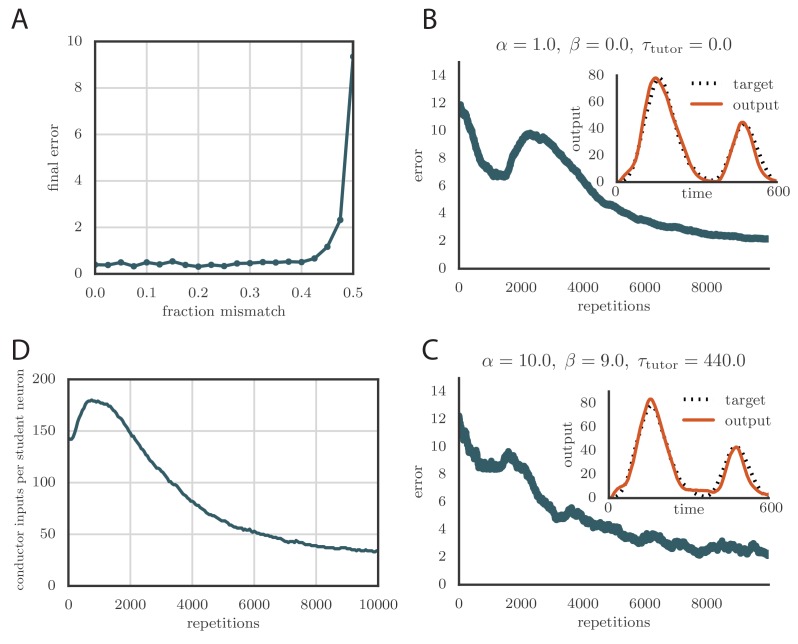
Figura 6.Assegnazione dei crediti e rafforzamento dell’apprendimento.(A) Effetti dell’errata assegnazione dei crediti sull’apprendimento in una simulazione basata sui tassi. Qui, il sistema ha appreso sequenze di output per due canali indipendenti. I pesi di uscita degli studenti Maj sono stati scelti in modo che il tutor abbia erroneamente assegnato una frazione dei neuroni degli studenti ad un canale di uscita diverso da quello su cui è stato effettivamente mappato. Il grafico mostra come la precisione dell’uscita del motore dopo 1000 passi di apprendimento dipendeva dalla frazione di credito erroneamente assegnata.(B) Curva di apprendimento e uscita del motore allenato (inset) per uno dei canali che mostra l’apprendimento a due fasi di rinforzo per il tutor senza memoria (τtutor=0). La precisione del modello addestrato è buona come nel caso in cui si è supposto che il tutor abbia un modello perfetto della relazione studente-uscita. Tuttavia, la velocità di apprendimento è ridotta. (Vedi Video online 6.)(C) Curva di apprendimento e uscita del motore addestrato (inset) per uno dei canali di uscita che mostra l’apprendimento a due fasi di rinforzo quando il circuito del tutor ha bisogno di integrare le informazioni sull’errore del motore in un certo lasso di tempo. Anche in questo caso l’apprendimento è stato lento, ma la precisione dello stato addestrato è rimasta invariata. (Vedi Video online 7.)(D) Evoluzione del numero medio di ingressi HVC per ogni neurone RA con l’apprendimento in un esempio di rinforzo. Le sinapsi sono state considerate potate se hanno ammesso una corrente inferiore a 1 nA dopo un picco presinaptico nelle nostre simulazioni.DOI:
http://dx.doi.org/10.7554/eLife.20944.012

Video 6.Evoluzione della potenza del motore durante l’apprendimento in una simulazione di spiking con un tutor di rinforzo.Qui il tutor era senza memoria (τtutor=0). Questo video si riferisce alla Figura 6B.DOI:
http://dx.doi.org/10.7554/eLife.20944.013

Video 7.Evoluzione della potenza del motore durante l’apprendimento in una simulazione di spiking con un tutor di rinforzo.Qui il tutor doveva integrare le informazioni sull’errore del motore su una scala temporale τtutor=440ms. Questo video si riferisce alla Figura 6C.DOI:
http://dx.doi.org/10.7554/eLife.20944.014
Discussione
Abbiamo costruito un modello di apprendimento in due fasi in cui un’area (l’allievo) impara a generare un modello di uscita del motore sotto la guida di un’area tutor. Questa architettura si ispira al sistema di canti dei fringuelli zebrati, dove l’area LMAN fornisce un bias correttivo al canto che viene poi consolidato nelle sinapsi HVC-RA. Utilizzando un approccio radicato nell’efficiente letteratura di codifica, abbiamo mostrato analiticamente che, in un modello semplice, l’output del tutor che più probabilmente porterà ad un apprendimento efficace da parte dello studente comporta un integrale rispetto alla recente entità dell’errore motorio. Abbiamo scoperto che l’efficienza richiede che il lasso di tempo per questo integrale sia correlato alla regola della plasticità sinaptica utilizzata dallo studente. Utilizzando simulazioni, abbiamo testato le nostre scoperte in impostazioni più generali. In particolare, abbiamo dimostrato che l’abbinamento tutor-studente è importante per l’apprendimento in un modello spiking-neurone costruito per riprodurre modelli di spiking simili a quelli misurati nei fringuelli zebrati. L’apprendimento in questo modello cambia le statistiche di spiking dei neuroni degli studenti in modo realistico, per esempio, producendo eventi di sparo più esplosivi e stereotipati man mano che l’apprendimento progredisce. Infine, abbiamo mostrato come il tutor può costruire il suo segnale di correzione degli errori attraverso l’apprendimento di rinforzo.
Se il sistema di birdsong supporta un apprendimento efficiente, il nostro modello può prevedere la struttura temporale dei modelli di sparo dei neuroni LMAN di proiezione RA, data la regola di plasticità implementata nelle sinapsi HVC-RA. Queste previsioni possono essere testate direttamente da registrazioni di neuroni LMAN in uccelli canterini, supponendo che sia disponibile una buona misura di errore motorio, e che possiamo stimare come i neuroni contribuiscono a questo errore. Inoltre, le registrazioni da un circuito di tutor, come LMAN, potrebbero essere combinate con una misura dell’errore motorio per dedurre la regola della plasticità in un circuito studentesco a valle, come RA. Questo potrebbe essere confrontato con misure dirette della regola di plasticità ottenuta in fetta. Al contrario, la conoscenza della regola di plasticità dell’allievo potrebbe essere usata per prevedere la dipendenza dal tempo dei tassi di accensione del tutor. Secondo il nostro modello, il rateo di cottura dovrebbe riflettere l’integrale dell’errore motorio con il tempo previsto dal modello. Un approccio diverso potrebbe essere quello di insegnare artificialmente a RA stimolando i neuroni LMAN elettricamente o optogeneticamente. Noi prevediamo che se il segnale del tutor viene fornito in modo appropriato( ad esempio, in combinazione con una particolare sillaba[Tumer and Brainard, 2007]), allora il bias premotorio prodotto dalla stimolazione dovrebbe diventare incorporato nel percorso motorio più velocemente quando la scala temporale del segnale LMAN artificiale è correttamente abbinato alla regola di plasticità sinaptica di RA.
Il nostro modello può essere applicato più in generale ad altri sistemi del cervello che presentano un apprendimento in due fasi, come l’apprendimento motorio nei mammiferi. Se i meccanismi di plasticità in questi sistemi sono diversi da quelli degli uccelli canori, le nostre previsioni sulla struttura del segnale guida variano di conseguenza. Questo permetterebbe di testare ulteriormente il nostro modello di “apprendimento efficiente” nel cervello. Vale la pena sottolineare che il nostro modello è stato derivato assumendo una certa gerarchia tra i tempi che modellano la plasticità dello studente e il segnale del tutor. Un disallineamento tra le previsioni e le osservazioni del modello potrebbe anche implicare una rottura di queste approssimazioni, piuttosto che il fallimento dell’ipotesi che il particolare sistema in studio si sia evoluto per supportare l’apprendimento efficiente. Naturalmente la nostra analisi potrebbe essere estesa rilassando queste ipotesi, per esempio mantenendo più termini nell’espansione di Taylor che abbiamo usato nella nostra derivazione del segnale del tutor abbinato.
Applicato al canto degli uccelli, il nostro modello è meglio visto come un meccanismo per l’apprendimento delle sillabe del canto. L’ordine delle sillabe nei motivi del canto sembra avere un secondo livello di controllo all’interno di HVC e forse anche oltre(Basista et al., 2014; Hamaguchi et al., 2016). Le canzoni possono anche essere distorte distorcendo la loro base temporale attraverso cambiamenti nella cottura HVC senza alterazioni della connettività HVC-RA (Aliet al., 2013). Alla luce di questi fenomeni, sarebbe interessante incorporare il nostro modello in un quadro gerarchico più ampio in cui si apprenda anche la sequenza e la struttura temporale delle sillabe. Un modello di transizione tra le sillabe si trova in Doya e Sejnowski (2000), dove gli autori utilizzano uno schema di ottimizzazione della “perturbazione del peso” in cui ogni peso sinaptico HVC-RA viene perturbato individualmente. Non abbiamo seguito questo approccio perché non esiste un meccanismo plausibile che permetta a LMAN di fornire una guida separata per ogni sinapsi HVC-RA; in particolare, non ci sono abbastanza neuroni LMAN (Fieteet al., 2007).
In questo articolo abbiamo ipotizzato un’architettura a due fasi per l’apprendimento, ispirata al canto degli uccelli. Una domanda interessante è se e a quali condizioni una tale architettura sia più efficace di un modello in un solo passo. Forse, avere due fasi è meglio quando un’unica area tutor è responsabile della formazione di diversi controller dedicati, come è probabile che sia il caso nell’apprendimento motorio. Sarebbe quindi vantaggioso avere un’area in grado di apprendere comportamenti arbitrari, magari a costo di utilizzare più risorse e di avere tempi di reazione più lenti, insieme alla capacità di trasferire questi comportamenti in circuiti di basso livello che sono in grado di produrre solo programmi motori stereotipati. Si pone quindi la questione se avere più di due livelli in questa gerarchia potrebbe essere utile, cosa potrebbero fare gli altri livelli, e se tali sistemi di apprendimento gerarchici sono implementati nel cervello.
Materiali e metodi
Equazioni per il modello basato sui tassi
Le equazioni di base che abbiamo usato per descrivere il nostro modello basato sui tassi(Figura 2A) sono le seguenti:(8)ya(t)=∑jMajsj(t)=∑jMajsj(t),sj(t)=∑iWijci(t)+wgj(t)-xinh.
Nelle simulazioni, abbiamo ulteriormente filtrato l’output utilizzando un kernel esponenziale,(9)y~a(t)=∑jMaj∫0tsj(t′)e-(t-t′)/τoutdt′,
con una scala temporale τout che di solito impostiamo a 25 ms. Lo smoothing produce output più realistici imitando il tempo di reazione relativamente lento dei muscoli reali, e stabilizza l’apprendimento filtrando le componenti ad alta frequenza dell’output del motore. Queste ultime interferiscono con l’apprendimento a causa del ritardo tra l’effetto dell’attività del conduttore sulle forze sinaptiche e l’uscita del motore. Questo ritardo è dell’ordine τ1,2-τout (vedi la regola di plasticità qui sotto).
L’attività del conduttore nel modello basato sul tasso è modellata in base al songbird HVC(Hahnloser et al., 2002): ogni neurone spara un singolo colpo durante il programma del motore. Ogni scoppio corrisponde ad un forte aumento del rateo di accensione ci(t) da 0 ad un valore costante, e poi una diminuzione 10ms dopo. Le attività dei diversi neuroni sono ripartite per tutta la durata del programma di uscita. Anche altre scelte per l’attività del conduttore funzionano, a condizione che non si ripetano gli schemi (vedi Appendice).
Descrizione matematica della regola di plasticità
Nel nostro modello il tasso di variazione dei pesi sinaptici obbedisce ad una regola che dipende da una versione filtrata del segnale del conduttore (vedi Figura 2B). Questo è espresso matematicamente come(10)dWijdt=ηc~i(t)(gj(t)-θ),
dove η è un tasso di apprendimento e c~i=K*ci, con la stella che rappresenta la convoluzione e K un kernel di filtraggio. Abbiamo considerato una combinazione lineare di due kernel esponenziali con tempi τ1 e τ2,(11)K(t)=αK1(t)-βK2(t),
con Ki(t) dato da(12)Ki(t)={τi-1e-t/τifort≥0,0else.
Scelte diverse per i kernel danno risultati simili (vedi Appendice). La scala complessiva di α e β può essere assorbita nel tasso di apprendimento η in Equazione (10 ). Nelle nostre simulazioni, fissiamo α-β=1 e manteniamo costante il tasso di apprendimento mentre cambiamo la regola di plasticità (vedi Equazione 3).
Nelle simulazioni di spiking con e senza apprendimento di rinforzo nel circuito del tutor, i ratei di cottura ci(t) e gj(t) sono stati stimati filtrando i treni di spike con i kernel esponenziali i cui tempi erano nell’intervallo 5ms-40ms. Gli studi di rinforzo in genere richiedevano tempi più lunghi per la stabilità, forse a causa dei ritardi tra l’attività del conduttore e i segnali di ricompensa.
Derivazione del segnale del tutor corrispondente
Per trovare il segnale del tutor che fornisce l’insegnamento più efficace per lo studente, calcoliamo prima di tutto quanto cambiano i pesi sinaptici secondo la nostra regola di plasticità, l’Equazione (10). Poi richiediamo che questo cambiamento corrisponda alla direzione di discesa del gradiente. Abbiamo(13)ΔWij=∫0TdWijdtdt=η∫0Tc~i(t)(gj(t)-θ)dt.
A causa delle ipotesi di linearità del nostro modello, è sufficiente concentrarsi su un caso in cui ogni neurone conduttore, i, spara una singola breve raffica, alla volta ti. Scriviamo questo come ci(t)=δ(t-ti), e così(14)ΔWij=∫0TdWijdtdt=η∫0TK(t-ti)(gj(t)-θ)dt,
dove abbiamo usato la definizione di c~i(t). Se le costanti di tempo τ1, τ2 sono brevi rispetto alla scala temporale su cui varia l’input del tutor gj(t), solo i valori di gj(t) intorno al tempo ti contribuiranno all’integrale. Se ipotizziamo inoltre che T≫ti, possiamo usare un’espansione di Taylor di gj(t) intorno a t=ti per eseguire il calcolo:(15)ΔWij≈η∫ti∞K(t-ti)(gj(ti)-θ+(t-ti)gj′(ti))dt=η(gj(ti)-θ)∫0∞K(t)dt+ηgj′(ti)∫0∞tK(t)dt=η(gj(ti)-θ)∫0∞(αK1(t)-βK2(t))dt+ηgj′(ti)∫0∞t(αK1(t)-βK2(t))dt.
Facendo gli integrali che coinvolgono i kernel esponenziali K1 e K2, otteniamo(16)ΔWij=η[(α-β)(gj(ti)-θ)+(ατ1-βτ2)gj′(ti)].
Vorremmo che questo cambiamento sinaptico riduca in modo ottimale una misura di disallineamento tra l’uscita e il target desiderato misurato da una funzione di perdita. Una funzione di perdita liscia generica L(ya(t),y¯a(t)) può essere approssimata quadraticamente quando ya è sufficientemente vicina al target y¯a(t). Con questo in mente, consideriamo una perdita quadratica(17)L=12∑a∫0T[ya(t)-y¯a(t)]2dt.
La funzione di perdita diminuirebbe monotonicamente durante l’apprendimento se i pesi sinaptici cambiassero in proporzione al gradiente negativo di L:(18)ΔWij=-γ∂L∂Wij,
dove γ e’ un tasso di apprendimento. Ciò implica(19)ΔWij=-γ∑a∫0TMaj[ya(t)-y¯a(t)]ci(t).
Utilizzando nuovamente ci(t)=δ(t-ti), otteniamo(20)ΔWij=-γϵj(ti),
dove abbiamo usato la notazione di Equazione (2) per l’errore motorio al neurone studente j.
Ora abbiamo impostato le equazioni (16) e (20) uguali tra loro. Se il conduttore spara densamente nel tempo, abbiamo bisogno dell’uguaglianza da mantenere per tutti i tempi, e così otteniamo un’equazione differenziale per il segnale del tutor gj(t). Questo identifica il segnale del tutor che porta all’apprendimento della discesa a gradiente in funzione dell’errore motore ϵj(t), Equazione (3) (con la notazione ζ=γ/η).
Simulazioni di Spiking
Per gli ingressi sinaptici abbiamo utilizzato modelli di spiking basati su neuroni integrato-e-fuoco a perdita con dinamica basata sulla corrente. La grandezza dei potenziali sinaptici generati dalle sinapsi conduttore-studente era indipendente dal potenziale di membrana, approssimando la dinamica del recettore AMPA, mentre gli input sinaptici dal tutor allo studente erano basati su una miscela di dinamiche AMPA e NMDA. In particolare, le equazioni che descrivono la dinamica del modello di picco erano:(21)τmdVjdt=(VR-Vj)+R(IjAMPA+IjNMDA)-Vinh,(eccetto durante il periodo refrattario)dIjAMPAdt=-IjAMPAτAMPA+∑iWij∑kδ(t-tk conduttore \#i)+(1-r)w∑kδ(t-tktutor),dIjNMDAdt=-IjNMDAτNMDA+rwG(Vj)∑kδ(t-tktutor),Vinh=ginhN student∑jSj(t),dSjdt=-Sjτinh+∑kδ(t-t-tkstudent),G(V)=[1+[Mg]3.57mMexp(-V/16.13mV)]-1.
Qui Vj è il potenziale di membrana del jth neurone studente e VR è il potenziale a riposo, così come il potenziale a cui la membrana è stata resettata dopo un picco. I picchi sono stati registrati ogni volta che il potenziale di membrana è andato al di sopra di una soglia Vth, dopo di che un periodo refrattario τref seguito. Oltre agli ingressi eccitatori AMPA e NMDA modellati dalle variabili IjAMPA e IjNMDA nel nostro modello, abbiamo anche incluso un segnale globale inibitorio Vinh che è proporzionale all’attività complessiva dei neuroni degli studenti mediata su una scala temporale τinh. La media viene eseguita utilizzando le variabili ausiliarie Sj che sono le convoluzioni dei treni di picco degli studenti con un kernel esponenziale. Queste possono essere pensate come un semplice modello per le attività degli interneuroni inibitori nello studente.
Latabella 1 fornisce i valori dei parametri che abbiamo usato nelle simulazioni. Questi valori sono stati scelti per corrispondere alle statistiche di cottura dei neuroni in RA aviaria, come descritto di seguito.10.7554/eLife.20944.015Tabella 1.Valori per i parametri utilizzati nelle simulazioni di spike.DOI:http://dx.doi.org/10.7554/eLife.20944.015ParametroSymbolValueParametroSymbolValueNo. di neuroni conduttori300No. di neuroni studenti80Reset potentialVR-72.3mVReset resistanceR353MΩThreshold potentialVth-48.6mVStrength di inhibitionginh1.80mCostante di tempo di inibizione della membrana di MVMτm24.5msFrazione dei recettori NMDA recettorir0.9Periodo refrattarioτref1.1msForza delle sinapsi da tutorw100nAAMPAcostante di tempoτAMPA6.3msNo. di sinapsi del conduttore per neurone studente148NMDAcostante di tempoτNMDA81.5msForza principale delle sinapsi da conduttore32.6nCostante di tempo per l’inibizione globaleτinh20msStandard deviazione standard dei pesi conduttore-studente17.4nAConductor frequenza di sparo del conduttore durante le raffiche632Hz
La dinamica di tensione per i neuroni del conduttore e del tutor non è stata simulata esplicitamente. Al contrario, si è supposto che ogni neurone conduttore sparasse una raffica ad un tempo fisso durante la simulazione. L’inizio di ogni scoppio aveva un jitter temporale additivo di ±0,3ms e ogni picco dello scoppio aveva un jitter di ±0,2ms. Questo ha modellato l’incertezza nei tempi di picco che si osserva in registrazioni in vivo nel canto degli uccelli(Hahnloser et al., 2002). I neuroni del tutor hanno sparato i picchi di Poisson con una velocità di sparo dipendente dal tempo che è stata impostata come descritto nel testo principale.
La connettività iniziale tra il conduttore e i neuroni dell’allievo è stata scelta per essere scarsa (vedi Tabella 1). La distribuzione iniziale dei pesi sinaptici è stata log-normale, con valori misurati sperimentalmente per i fringuelli zebrati(Garst-Orozco et al., 2014). Poiché queste misurazioni vengono effettuate nella fetta, è probabile che il numero assoluto di sinapsi HVC per ogni neurone RA sia stato sottovalutato. Il numero di sinapsi del conduttore-studente con cui iniziamo le nostre simulazioni è quindi scelto per essere superiore al valore riportato in quel documento (vedi Tabella 1), e può cambiare durante l’apprendimento. Abbiamo verificato che il paradigma di apprendimento qui descritto è robusto a cambiamenti sostanziali di questi parametri, ma abbiamo scelto valori che sono fedeli agli esperimenti del canto degli uccelli e che sono quindi in grado di imitare le statistiche di picco della RA durante il canto.
Le sinapsi proiettate su ogni neurone dello studente dal tutor hanno un peso che viene fissato durante le nostre simulazioni riflettendo la constatazione di Garst-Orozco et al. (2014) che la forza media delle sinapsi LMAN-RA per i fringuelli zebrati non cambia con l’età. Ci sono prove che le singole sinapsi LMAN-RA subiscono la plasticità in concomitanza con le sinapsi HVC-RA (Mehaffeye Doupe, 2015), ma nonabbiamo cercato di modellare questo effetto. Ci sono anche cambiamenti nello sviluppo della cinetica delle correnti sinaptiche mediate da NMDA sia nelle sinapsi HVC-RA che LMAN-RA che non modelliamo (Starke Perkel, 1999). Queste, tuttavia, avvengono all’inizio dello sviluppo, e quindi è improbabile che abbiano un effetto sulla cristallizzazione del canto, che è ciò su cui si concentra il nostro modello. Stark e Perkel, 1999 hanno anche osservato cambiamenti nel contributo relativo della NMDA alle risposte dell’AMPA nelle sinapsi HVC-RA. Non incorporiamo tali effetti nel nostro modello, poiché non modelliamo esplicitamente le dinamiche dei neuroni HVC in questo documento. Tuttavia, questa è una strada interessante per il lavoro futuro, soprattutto perché è dimostrato che anche l’HVC può contribuire all’apprendimento, in particolare in relazione alla struttura temporale del canto(Ali et al., 2013).
Abbinare le statistiche di picco con i dati sperimentali
Abbiamo usato una tecnica di ottimizzazione per scegliere i parametri per massimizzare la somiglianza tra le statistiche di picco nelle nostre simulazioni e le statistiche di sparo osservate nelle registrazioni neurali dell’uccello canterino. Il confronto si è basato su diverse statistiche descrittive: la velocità media di sparo, il coefficiente di variazione e l’asimmetria della distribuzione degli intervalli tra le spire, la frequenza e la durata media delle raffiche e la velocità di sparo durante le raffiche. Per il calcolo di queste statistiche, le raffiche sono state definite per iniziare se il rateo di cottura è andato al di sopra di 80 Hz e durare fino a quando il rateo è sceso al di sotto di 40 Hz.
Per effettuare tali ottimizzazioni nel contesto stocastico delle nostre simulazioni, abbiamo utilizzato un algoritmo evolutivo, la strategia evolutiva di adattamento della matrice di covarianza (CMA-ES) (Hansen, 2006). La funzione obiettivo era basata sull’errore relativo tra le statistiche di simulazione xisim e le statistiche xiobs osservate,(22)error=[∑i(xisimxiobs-1)2]1/2.
Il peso uguale è stato posto sull’ottimizzazione della statistica di cottura nel giovane (basata su una registrazione da un uccello a 43 dph) e sull’ottimizzazione della cottura nell’adulto (basata su una registrazione da un uccello a 160 dph). In questa ottimizzazione non c’è stato alcun apprendimento tra la fase giovanile e quella adulta. Abbiamo semplicemente richiesto che il numero di sinapsi HVC per neurone RA e la deviazione media e standard dei corrispondenti pesi sinaptici fossero negli intervalli visti nel giovane e nell’adulto da Garst-Orozco et al. (2014). L’ottimizzazione è stata effettuata in Python (RRID:SCR_008394), utilizzando il codice di https://www.lri.fr/~hansen/cmaes_inmatlab.html. I risultati hanno fissato le scelte dei parametri nella Tabella 1 che sono state poi utilizzate per studiare il nostro paradigma di apprendimento. Mentre queste scelte sono importanti per ottenere statistiche di cottura che sono simili a quelle viste nelle registrazioni dall’uccello, il nostro paradigma di apprendimento è robusto alle grandi variazioni dei parametri nella Tabella 1.
Software e dati
Abbiamo utilizzato il codice Python (RRID:SCR_008394) per le simulazioni e l’analisi dei dati. Il software e i dati che abbiamo utilizzato sono accessibili online su GitHub (RRID:SCR_002630) all’indirizzo https://github.com/ttesileanu/twostagelearning.
References
- Ali F, Otchy TM, Pehlevan C, Fantana AL, Burak Y, Ölveczky BP. The basal ganglia is necessary for learning spectral, but not temporal, features of birdsong. Neuron. 2013; 80:494-506. DOI | PubMed
- Andalman AS, Fee MS. A basal ganglia-forebrain circuit in the songbird biases motor output to avoid vocal errors. PNAS. 2009; 106:12518-12523. DOI | PubMed
- Basista MJ, Elliott KC, Wu W, Hyson RL, Bertram R, Johnson F. Independent premotor encoding of the sequence and structure of birdsong in avian cortex. Journal of Neuroscience. 2014; 34:16821-16834. DOI | PubMed
- Canady RA, Burd GD, DeVoogd TJ, Nottebohm F. Effect of testosterone on input received by an identified neuron type of the canary song system: a golgi/electron microscopy/degeneration study. Journal of Neuroscience. 1988; 8:3770-3784. PubMed
- Chistiakova M, Bannon NM, Bazhenov M, Volgushev M. Heterosynaptic plasticity: multiple mechanisms and multiple roles. The Neuroscientist : A Review Journal Bringing Neurobiology, Neurology and Psychiatry. 2014; 20:483-498. DOI | PubMed
- Chistiakova M, Volgushev M. Heterosynaptic plasticity in the neocortex. Experimental Brain Research. 2009; 199:377-390. DOI | PubMed
- Doya K, Sejnowski TJ. The New Cognitive Neurosciences. arXiv:1011.1669v3; 2000.
- Farries MA, Fairhall AL. Reinforcement learning with modulated spike timing dependent synaptic plasticity. Journal of Neurophysiology. 2007; 98:3648-3665. DOI | PubMed
- Fee MS, Goldberg JH. A hypothesis for basal ganglia-dependent reinforcement learning in the songbird. Neuroscience. 2011; 198:152-170. DOI | PubMed
- Fiete IR, Fee MS, Seung HS. Model of birdsong learning based on gradient estimation by dynamic perturbation of neural conductances. Journal of Neurophysiology. 2007; 98:2038-2057. DOI | PubMed
- Fiete IR, Seung HS. Gradient learning in spiking neural networks by dynamic perturbation of conductances. Physical Review Letters. 2006; 97DOI | PubMed
- Frankland PW, Bontempi B. The organization of recent and remote memories. Nature Reviews Neuroscience. 2005; 6:119-130. DOI | PubMed
- Gadagkar V, Puzerey PA, Chen R, Baird-Daniel E, Farhang AR, Goldberg JH. Dopamine neurons encode performance error in singing birds. Science. 2016; 354:1278-1282. DOI | PubMed
- Garst-Orozco J, Babadi B, Ölveczky BP. A neural circuit mechanism for regulating motor variability during skill learning. eLife. 2014; 3DOI | PubMed
- Hahnloser RH, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002; 419:65-70. DOI | PubMed
- Hamaguchi K, Tanaka M, Mooney R. A distributed recurrent network contributes to temporally precise vocalizations. Neuron. 2016; 91:680-693. DOI | PubMed
- Hansen N. Towards a New Evolutionary Computation. Advances on Estimation of Distribution Algorithms. 2006.
- Herrmann K, Arnold AP. The development of afferent projections to the robust archistriatal nucleus in male zebra finches: a quantitative Electron microscopic study. Journal of Neuroscience. 1991; 11:2063-2074. PubMed
- Hoffmann LA, Saravanan V, Wood AN, He L, Sober SJ. Dopaminergic contributions to vocal learning. Journal of Neuroscience. 2016; 36:2176-2189. DOI | PubMed
- Immelmann K. Bird Vocalizations. 1969.
- Kao MH, Wright BD, Doupe AJ. Neurons in a forebrain nucleus required for vocal plasticity rapidly switch between precise firing and variable bursting depending on social context. Journal of Neuroscience. 2008; 28:13232-13247. DOI | PubMed
- Kawai R, Markman T, Poddar R, Ko R, Fantana AL, Dhawale AK, Kampff AR, Ölveczky BP. Motor cortex is required for learning but not for executing a motor skill. Neuron. 2015; 86:800-812. DOI | PubMed
- Kojima S, Kao MH, Doupe AJ. Task-related "cortical" bursting depends critically on basal ganglia input and is linked to vocal plasticity. PNAS. 2013; 110:4756-4761. DOI | PubMed
- Kubikova L, Kostál L, KošÅ¥ál L. Dopaminergic system in Birdsong learning and maintenance. Journal of Chemical Neuroanatomy. 2010; 39:112-123. DOI | PubMed
- Leonardo A, Fee MS. Ensemble coding of vocal control in birdsong. Journal of Neuroscience. 2005; 25:652-661. DOI | PubMed
- Lynch GF, Okubo TS, Hanuschkin A, Hahnloser RH, Fee MS. Rhythmic Continuous-Time coding in the songbird analog of vocal motor cortex. Neuron. 2016; 90:877-892. DOI | PubMed
- Mehaffey WH, Doupe AJ. Naturalistic stimulation drives opposing heterosynaptic plasticity at two inputs to songbird cortex. Nature Neuroscience. 2015; 18:1272-1280. DOI | PubMed
- Memmesheimer RM, Rubin R, Olveczky BP, Sompolinsky H. Learning precisely timed spikes. Neuron. 2014; 82:925-938. DOI | PubMed
- Perkel DJ. Origin of the anterior forebrain pathway. Annals of the New York Academy of Sciences. 2004; 1016:736-748. DOI | PubMed
- Picardo MA, Merel J, Katlowitz KA, Vallentin D, Okobi DE, Benezra SE, Clary RC, Pnevmatikakis EA, Paninski L, Long MA. Population-Level representation of a temporal sequence underlying song production in the zebra finch. Neuron. 2016; 90:866-876. DOI | PubMed
- Seung HS. Learning in spiking neural networks by reinforcement of stochastic synaptic transmission. Neuron. 2003; 40:1063-1073. DOI | PubMed
- Simpson HB, Vicario DS. Brain pathways for learned and unlearned vocalizations differ in zebra finches. Journal of Neuroscience. 1990; 10:1541-1556. PubMed
- Spiro JE, Dalva MB, Mooney R. Long-range inhibition within the zebra finch song nucleus RA can coordinate the firing of multiple projection neurons. Journal of Neurophysiology. 1999; 81:3007-3020. PubMed
- Stark LL, Perkel DJ. Two-stage, input-specific synaptic maturation in a nucleus essential for vocal production in the zebra finch. Journal of Neuroscience. 1999; 19:9107-9116. PubMed
- Teşileanu T. GitHub. 2016.
- Tumer EC, Brainard MS. Performance variability enables adaptive plasticity of ‘crystallized’ adult birdsong. Nature. 2007; 450:1240-1244. DOI | PubMed
- Turner RS, Desmurget M. Basal ganglia contributions to motor control: a vigorous tutor. Current Opinion in Neurobiology. 2010; 20:704-716. DOI | PubMed
- Veit L, Aronov D, Fee MS. Learning to breathe and sing: development of respiratory-vocal coordination in young songbirds. Journal of Neurophysiology. 2011; 106:1747-1765. DOI | PubMed
- Warren TL, Tumer EC, Charlesworth JD, Brainard MS. Mechanisms and time course of vocal learning and consolidation in the adult songbird. Journal of Neurophysiology. 2011; 106:1806-1821. DOI | PubMed
- Yu AC, Margoliash D. Temporal hierarchical control of singing in birds. Science. 1996; 273:1871-1875. DOI | PubMed
- Ölveczky BP, Andalman AS, Fee MS. Vocal experimentation in the juvenile songbird requires a basal ganglia circuit. PLoS Biology. 2005; 3DOI | PubMed
- Ölveczky BP, Otchy TM, Goldberg JH, Aronov D, Fee MS. Changes in the neural control of a complex motor sequence during learning. Journal of Neurophysiology. 2011; 106:386-397. DOI | PubMed
Fonte
Teşileanu T, Ölveczky B, Balasubramanian V, Frank MJ () Rules and mechanisms for efficient two-stage learning in neural circuits. eLife 6e20944. https://doi.org/10.7554/eLife.20944





